Breaking Combined Multiple Recursive Generators
서론
10월 중에 제가 속한 CTF 팀 perfect blue에서 pbctf 2021을 주최했습니다.
CTF를 준비하면서 다양한 암호학 논문들을 읽어보았는데, 그 중에서도 참고할만한 흥미로운 공격이 있어서 Yet Another PRNG라는 문제로 작성하게 되었습니다.

해당 문제는 CMRG(Combined Multiple Recursive Generator)라는 PRNG의 선형성을 공격하는 문제로, 이 논문의 5절에서 공격의 원형을 살펴볼 수 있습니다.
본론
CMRG
CMRG는 2개의 LCG를 혼합한 형태입니다. 서로소인 $m1, m2$가 존재할 때,
$x_i = a_{11} x_{i-1} + a_{12}x_{i-2} + a_{13} x_{i-3} \mod m_1$ $y_i = a_{21} y_{i-1} + a_{22}y_{i-2} + a_{23} y_{i-3} \mod m_2$ $z_i = x_i - y_i \mod m_1$
의 구조로 구성되어 있고, $z_i$ 가 output이 되는 꼴입니다. $m_1, m_2$는 비슷한 크기를 가집니다.
이를 훑어보면 두 가지 의문을 가질 수 있습니다.
- $z_i = x_i - y_i \mod m_1$ 에서, 보통의 경우 $z_i = x_i - y_i$ 거나 $z_i = x_i - y_i + m_1$ 인 거 아닌가?
- $m_1$과 $m_2$ 가 서로소라면 중국인의 나머지 정리(CRT)를 적용할 여지가 있는 것이 아닌가?
Attacking CMRG - Part 1 (CRT)
우선 두 번째 의문부터 적용을 시켜봅시다. $\text{mod }m_1$ 상의 $x_i$와 $\text{mod } m_2$ 상의 $y_i$를 합쳐서 $\text{mod } m_1m_2$ 상의 $X_i$를 정의하는 것입니다.
이를 바탕으로 $A, B, C$를 다음과 같이 정의합시다.
$A = a_{11} \mod m_1, A = a_{21} \mod m_2$ $B = a_{12} \mod m_1, B = a_{22} \mod m_2$ $C = a_{13} \mod m_1, A = a_{23} \mod m_2$
그러면 다음과 같은 관계식을 얻을 수 있습니다.
$X_i = AX_{i-1} + BX_{i-2} + CX_{i-3} \mod m_1m_2$ $X_i = x_i \mod m_1, X_i = y_i \mod m_2$
실제로 $x_i, y_i$ 값이 어떤 지는 알 수 없지만, 이를 바탕으로 공격에 적용해보도록 합시다.
Attacking CMRG - Part 2 (LLL)
두 번째로 주목할 것은 첫 번째 의문입니다. $m_1$과 $m_2$는 비슷한 값을 가지기 때문에, 실제 $x_i - y_i$ 값을 brute-force 하는 것이 가능합니다.
$z_i’ = x_i - y_i$로 정의하면, $z_i’ = z_i$ 이거나 $z_i = z_i - m_1$임을 알 수 있습니다. 곧, $k$개의 output이 있을 때 $2^k$ 번의 brute-force를 통해서 올바른 $x_i - y_i$ 값들을 찍어볼 수 있습니다.
이 때 다음과 같이 생각을 넓혀봅시다:
어떤 정수 $k_i, \hat{k_i}$에 대해서, $X_i = k_i m_1 + x_i = \hat{k_i}m_2 + y_i$를 만족함을 알고 있습니다. 이 때 $z_i’ = x_i - y_i$ 이므로, $z_i’ = x_i - y_i = \hat{k_i}m_2 - k_im_1$ 임을 알 수 있고, 그러므로 $k_i = -z_i’ m_1^{-1} \mod m_2$ 임을 알 수 있습니다. 이 때, $X_i$가 $m_1m_2$ 보다 작다고 생각하면, $k_i$ 또한 $m_2$보다 작으므로 해당 값이 $k_i$ 값이라고 생각해볼 수 있습니다.
이를 바탕으로 다음과 같은 $P_i$를 생각하는 것이 가능합니다.
$P_i(v_i, v_{i+1}, v_{i+2}, v_{i+3}) = k_{i+3}m_1 + v_{i+3} - A(k_{i+2}m_1 + v_{i+2}) - B(k_{i+1}m_1 + v_{i+1}) - C(k_im_1 + v_i)$
이 때 이를 만족하는 $v$에 대해서 생각해보면, lattice를 정의할 수 있습니다. 예를 들어서, $v_0, v_1, v_2, v_3$ 에 대해서 lattice를 정의하면 다음과 같습니다.
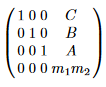
여기서 핵심 사항은 이를 통해서 항상 구할 수 있는가? 입니다. 답은 아니다입니다. LLL이 구할 수 있는 답의 범위는 정의한 lattice의 determinant의 크기에 비례합니다. 만약 여기서 더 정확하게 답을 구하고 싶다면, lattice의 크기를 늘려야만 합니다.
다행히도, 여기서 한 차례 더 나아가서 $v_0, v_1, v_2, v_3, v_4, v_5$ 에 대해서 식을 정의하는 것이 가능합니다. 이 경우 $v_3, v_4, v_5$를 $v_0, v_1, v_2$ 에 대한 식으로 정의하면 됩니다.
이를 통해 얻을 수 있는 lattice는 다음과 같습니다. (여기서 5열에 틀린 정보가 하나 있습니다. 꼭 직접 계산해보고 틀린 부분을 찾아보세요.)
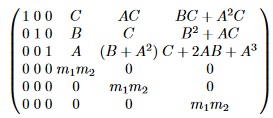
또한 더 나아가서 7x7 lattice를 다음과 같이 정의할 수 있습니다. (이 쪽 5열도 마찬가지로 틀린 정보가 하나 있습니다.)
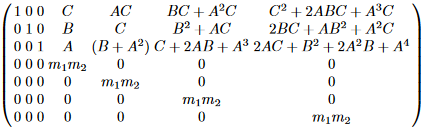
이렇게 늘릴 수록, 답의 범위는 $sqrt(\text{size of lattice})$에 비례합니다. 즉 마지막 lattice는 첫 lattice보다 $\sqrt{7}/\sqrt{4}$ 배 정확하다고 볼 수 있는 것이죠.
##Yet Another PRNG
pbctf에 나온 Yet Another PRNG의 코드를 살펴봅시다.
#!/usr/bin/env python3
from Crypto.Util.number import *
import random
import os
from flag import flag
def urand(b):
return int.from_bytes(os.urandom(b), byteorder='big')
class PRNG:
def __init__(self):
self.m1 = 2 ** 32 - 107
self.m2 = 2 ** 32 - 5
self.m3 = 2 ** 32 - 209
self.M = 2 ** 64 - 59
rnd = random.Random(b'rbtree')
self.a1 = [rnd.getrandbits(20) for _ in range(3)]
self.a2 = [rnd.getrandbits(20) for _ in range(3)]
self.a3 = [rnd.getrandbits(20) for _ in range(3)]
self.x = [urand(4) for _ in range(3)]
self.y = [urand(4) for _ in range(3)]
self.z = [urand(4) for _ in range(3)]
def out(self):
o = (2 * self.m1 * self.x[0] - self.m3 * self.y[0] - self.m2 * self.z[0]) % self.M
self.x = self.x[1:] + [sum(x * y for x, y in zip(self.x, self.a1)) % self.m1]
self.y = self.y[1:] + [sum(x * y for x, y in zip(self.y, self.a2)) % self.m2]
self.z = self.z[1:] + [sum(x * y for x, y in zip(self.z, self.a3)) % self.m3]
return o.to_bytes(8, byteorder='big')
if __name__ == "__main__":
prng = PRNG()
hint = b''
for i in range(12):
hint += prng.out()
print(hint.hex())
assert len(flag) % 8 == 0
stream = b''
for i in range(len(flag) // 8):
stream += prng.out()
out = bytes([x ^ y for x, y in zip(flag, stream)])
print(out.hex())
겉보기에는 CMRG보다 조금 더 어려운 것처럼 보입니다.
하지만 유일하게 다른 점은 둘이 있습니다. 첫 번째는 $z_i’$를 구하는 방법입니다. 이 경우 $z_i - 2*M$부터 $z_i + M$까지 4가지의 값으로 나뉩니다. 두 번째는 $k_i$의 값을 구하는 방법입니다. 이 경우 $k_i$ 의 값은 $(-2m_1^2)^{-1} z_i’$가 될 것입니다.
이를 바탕으로 solver를 작성해봅시다. 이 때 Lattice의 마지막 열에 answer row를 추가했습니다. 이는 Kannan embedding으로 자세한 것은 rkm님의 PPT를 참조해주세요. Link
#!/usr/bin/env sage
from Crypto.Util.number import *
import itertools
import random
from gen import PRNG
outputs = []
with open('output.txt', 'r') as f:
line = f.readline()
for i in range(12):
outputs.append(int(line[16 * i:16 * i + 16], 16))
enc = bytes.fromhex(f.readline().strip())
m1 = 2 ** 32 - 107
m2 = 2 ** 32 - 5
m3 = 2 ** 32 - 209
M = 2 ** 64 - 59
rnd = random.Random(b'rbtree')
a1 = [rnd.getrandbits(20) for _ in range(3)]
a2 = [rnd.getrandbits(20) for _ in range(3)]
a3 = [rnd.getrandbits(20) for _ in range(3)]
A = crt([a1[2], a2[2], a3[2]], [m1, m2, m3])
B = crt([a1[1], a2[1], a3[1]], [m1, m2, m3])
C = crt([a1[0], a2[0], a3[0]], [m1, m2, m3])
RANGE = 8
for x in itertools.product(range(-1, 3), repeat=RANGE):
print(x)
o = [outputs[i] - x[i] * M for i in range(RANGE)]
k = [inverse(-2 * m1 * m1, m2 * m3) * o[i] % (m2 * m3) for i in range(RANGE)]
mat = [[0 for j in range(2 * RANGE - 2)] for i in range(2 * RANGE - 2)]
for i in range(RANGE):
mat[i][i] = 1
for i in range(RANGE - 3):
mat[i][RANGE + i] = -C
mat[i + 1][RANGE + i] = -B
mat[i + 2][RANGE + i] = -A
mat[i + 3][RANGE + i] = 1
mat[RANGE + i][RANGE + i] = m1 * m2 * m3
mat[-1][RANGE + i] = (k[i + 3] - A * k[i + 2] - B * k[i + 1] - C * k[i]) * m1 % (m1 * m2 * m3)
T = 2 ** 33
mat[-1][-1] = T
mat = Matrix(mat)
mat = mat.LLL()
for i in range(2 * RANGE - 2):
flag = True
for j in range(RANGE - 4):
if mat[i][RANGE + j] != 0:
flag = False
break
if flag and (mat[i][-1] == T or mat[i][-1] == -T):
x_recov = list(map(int, mat[i][:RANGE]))
x_recov[-1] -= mat[i][-2]
print(x_recov)
y_recov = []
for i in range(RANGE):
y_recov.append(int((2 * m1 * x_recov[i] - o[i]) * inverse(m3, m2) % m2))
print(y_recov)
z_recov = []
for i in range(RANGE):
z_recov.append(int((2 * m1 * x_recov[i] - o[i] - m3 * y_recov[i]) // m2))
print(z_recov)
prng = PRNG()
prng.x = x_recov[:3]
prng.y = y_recov[:3]
prng.z = z_recov[:3]
flag = True
for i in range(12):
if outputs[i] != int(prng.out().hex(), 16):
flag = False
break
if flag:
stream = b''
for i in range(len(enc) // 8):
stream += prng.out()
print(bytes([x ^^ y for x, y in zip(enc, stream)]))
exit(0)
이를 바탕으로 얻을 수 있는 플래그는 pbctf{Wow_how_did_you_solve_this?_I_thought_this_is_super_secure._Thank_you_for_solving_this!!! 입니다.
결론
본래 다른 주제에 대해서 개인 연구를 진행하고 있었는데, 역시 저번 달과 같이 결과가 잘 나오지 않았습니다. 암호학에 대해서 개인 연구를 진행하는 것은 너무나 어려운 일이라는 것을 다시금 한 번 느꼈습니다. 그럼에도 불구하고 다른 곳에서는 찾아볼 수 있는 암호학 정보를 한국어로 작성하고 있기 때문에, 많은 분들에게 도움이 될 수 있기를 바라고 있습니다.
참고 문헌
- Attacks on Pseudo Random Number Generators Hiding a Linear Structure https://eprint.iacr.org/2021/1204.pdf
- https://github.com/rkm0959/rkm0959_presents/blob/main/lattice_survey.pdf