Casual Inference and Diagram
Introduction
Simpson’s Paradox
한 제약회사가 어떤 질병에 대해 치료제를 개발한 후 이 치료제가 실제로 효과가 있는지 700명의 환자들을 대상으로 실험을 진행하였다. 환자들의 3개월간 회복 경과를 지켜본 결과 아래와 같이 나타났다.
| 치료제 사용 | 치료제 미사용 | |
|---|---|---|
| 남성 | 81/87 회복 (93%) | 234/270 회복 (87%) |
| 여성 | 192/263 회복 (73%) | 55/80 회복 (69%) |
| 합산 | 273/350 회복 (78%) | 289/350 회복 (83%) |
각각의 성별에 대해서는 분명 치료제를 사용한 경우에 더 회복률이 높았지만, 합산 회복률은 치료제를 사용하지 않았을 때 오히려 더 높게 나타났다.
그러면 의사는 환자의 성별을 모르면 처방하지 않고, 알고 있다면 치료제를 처방해야 하는 마치 양자역학에서나 일어날 법한 일이 발생한 것일까?
물론 답은 “그렇지 않다” 이다. 이 결과를 올바르게 해석하기 위해서는 결과에 영향을 미치는 배경에 대한 이해가 있어야 한다. 통계에서 성별이 회복률과 상관관계가 존재함을 알 수 있다. 성별과 회복률 사이에 인과관계가 존재하는 경우를 가정해보자. 여성의 성호르몬이 회복을 저해하는 경우가 이에 해당할 것이다. 이 때 성별은 회복률 및 치료제 사용 여부에 모두 영향을 주었다고 볼 수 있다. 따라서, 치료제의 효과에 대해 분석하기 위해서는 성별에 대한 영향을 배제하고 남성과 여성의 통계를 따로 보는 것이 올바르다.
위 경우에는 남성과 여성에 대한 통계를 분리하여 해석하는것이 올바르지만, 분리하여 보는 것이 항상 올바르다고 할 수는 없다.
또다른 700명의 환자들에 대해 실험을 진행하고, 3개월 뒤에 혈압을 측정하여 혈압이 120 이상인 환자와 120 미만인 환자에 대한 경과는 아래와 같이 나타났다고 한다.
| 치료제 미사용 | 치료제 사용 | |
|---|---|---|
| 수축기혈압 130↓ | 81/87 회복 (93%) | 234/270 회복 (87%) |
| 수축기혈압 130↑ | 192/263 회복 (73%) | 55/80 회복 (69%) |
| 합산 | 273/350 회복 (78%) | 289/350 회복 (83%) |
각 항목의 Joint distribtution만 따졌을 때는 두 실험이 치료제 사용 여부만 뒤바뀌었을 뿐 완전히 동일하다. 그러나 아래 실험을 위 실험처럼 분석하면 잘못된 해석을 얻을 수 있다.
치료제를 사용했을 때 혈압을 낮추어주는 효과가 존재한다는 사실을 알고 있다고 하자. 이전 결과에서는 성별이 치료제 사용 여부 및 회복률에 영향을 주는 요인이었지만 이번 통계에서는 치료제 사용 여부가 혈압 및 회복률에 영향을 미치는 인과관계가 존재한다. 치료제가 회복률에 어떤 영향을 미치는지를 분석하고 싶다면, 이 경우에는 높은 혈압과 낮은 혈압의 실험군 각각에 대한 통계에 대해 해석하는 것이 올바르지 않고, 합산 결과로부터 해석을 해야 한다.
위 두 가지 실험은 인과관계를 명확히 알고 있을 때만 결과를 어떻게 해석해야할지 파악이 가능하다. 그렇지 않은 경우 실험 결과로부터 여러 가지 해석이 가능하고 어느 것이 맞는지 확신할 수 없기 때문에 의도에 따라 왜곡이 얼마든지 가능하다.
Causal Diagram
Cause
변수 $X$, $Y$에 대해, $Y$의 값이 $X$에 의존한다면, $X$를 $Y$의 cause라고 한다. 변수들을 vertex로 놓고 변수 $X$가 $Y$의 cause라면 $X$에서 $Y$로 directed edge를 생성하여 만든 그래프를 생각하자. 이를 Casual Diagram이라고 한다.
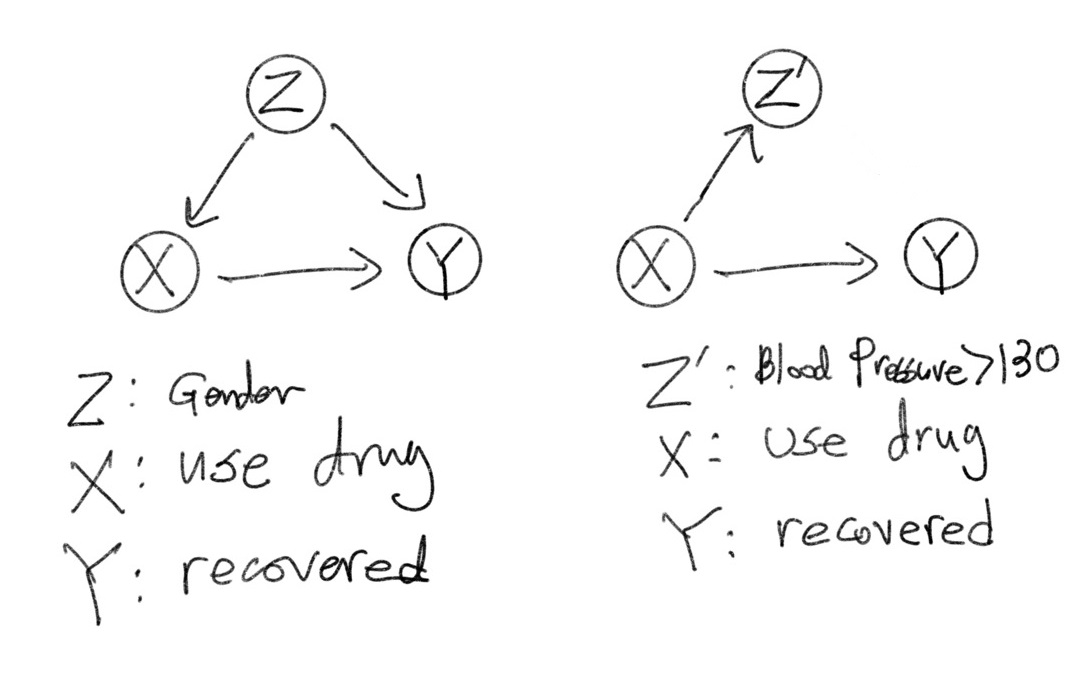
위 그림은 두 가지 실험을 Causal Diagram으로 나타낸 것이다.
첫 번째 실험은 성별($Z$)이 치료제 사용 여부($X$)와 회복률($Y$)의 Cause이고, 치료제 사용 여부($X$) 또한 회복률($Y$)의 Cause이다.
두 번째 실험은 치료제 사용 여부($X$)가 혈압($Z’$)와 회복률($Y$)의 Cause인 경우이다.
Structural Casual Model
Definition 1. 다음과 같이 구성되는 $M$을 Structural Causal Model이라 한다.
$M := (V, U, F, P(U))$
- $V = { V_1, V_2, .., V_n }$ 은 endogenous variables
- $U$ 는 exogenous variable들의 집합
- $F = { f_1, f_2, .., f_n }$ 에서 $f_i$는 $v_i$를 결정하는 함수들이다. 즉, $v_i \leftarrow f_i(\textbf{pa}_i, u_i)$ (단, $\textbf{pa}_i \subset V \setminus { V_i } $ )
- $P(U)$ 는 $U$에 대한 distribution
여기서 endogenous variable은 모델에서 결과로서 나타나 측정할 수 있는 값 (observable), exdogenous variable은 원인으로서만 나타나서 계측되지 않는 값(unobservable)을 뜻한다.
위 정의에서나 앞으로 사용할 notation에서 $V_i$와 같이 대문자인 것은 random varibale, $v_i$와 같이 소문자로 표현한 것은 그에 해당하는 값이다.
Example
Introduction에서와 같이 간단한 이야기를 통해 SCM에 대해 좀더 알아보자.
도시에 전염병이 돌아 많은 사람들이 죽고 있는 상황에서, 한 제약회사에서 이를 치료하기 위한 약을 만들었다. 사람들은 그 소문을 듣고 큰 비용을 지출해서라도 그 약을 테스트하는 실험에 참가하고자 했고, 실제로 실험 결과 해당 약을 먹은 사람들은 거의 죽지 않았다. 그 결과 해당 약을 대량 생산해 도시의 모든 환자들에게 무료로 나누어주었으나, 오히려 사망자 수는 증가하는 일이 발생하였다. 어떻게 이런 일이 발생하였을까?
실제로 일어난 일은 다음과 같다: 해당 약은 아무런 효과가 없었으며, 오히려 특정 유전자 형질 $g$를 가진 환자의 경우 자연 치유력이 존재하여 살 수 있지만 이를 억제하는 역할을 함이 밝혀졌다. 하지만 테스트를 받은 사람들은 많은 돈을 부담할 수 있는 고소득층이었는데, 고소득층의 사람들은 애초에 전염병을 이겨낼 만한 환경에서 살고 있었기 때문에 사망률이 원래 낮았던 것이다.
이를 SCM 으로 모델링해보자.
각 환자에 대해, 다음과 같은 endogenous variable 3가지를 정의하자.
- $R$ : 해당 환자가 고소득층이면 1, 아니면 0
- $D$ : 해당 환자가 약을 먹었으면 1, 아니면 0
- $A$ : 해당 환자가 치료되었으면 1, 죽었다면 0
또한 아래와 같은 exdogenous variable 2가지를 정의하자.
- $U_R$ : $R$에 영향을 끼치는 factor
- $U_G$ : 유전형질 $g$를 가지고 있으면 1, 아니면 0
각 endogenous variable에 대해 다음과 같은 함수들을 정의하자.
- $ f_R : U_R $
- $ f_D : R $
- $ f_A : R \lor (\lnot D \land U_G) $ (고소득층이거나, 약을 먹지 않았으며 유전형질 $g$를 가진 사람만 생존)
$U$에 대한 distribution은 $P(U_R = 1) = \frac{1}{2}, P(U_G = 1) = \frac{1}{2}, P(U) = P(U_R)P(U_G)$ 로 정의하자.
\[M = (V = \{R, D, A\}, U = \{ U_R, U_G \}, F = \{ f_R, f_D, f_A \}, P(U) )\]은 위 설정에 대한 SCM으로 볼 수 있다.
한편, 위 모델에서 약 사용에 따른 생존 여부의 조건부 확률을 구해보면 $ P(A \mid D) = 1, P(A \mid \lnot D) = \frac{1}{2} $ 이다.
약을 사용한 사람은 모두 $R = 1$에 해당하기 때문에 생존하고, 약을 사용하지 않은 사람들은 $U_G = 1$ 이어야 생존할 수 있기 때문에 $\frac{1}{2}$의 확률로 생존한다. 즉, conditional probability로 판단했을 때는 약 사용이 생존에 긍정적인 영향을 끼친다고 볼 수 있다.
그러나 실제로는 모든 사람에 대해 약을 줄 경우에 총 생존률은 $\frac{1}{2}$ 로, 약을 주지 않았을 때의 생존률인 $\frac{3}{4}$보다 작다.
따라서, 두 endogenous variable $X, Y$에 대해 $P(y \mid x)$ 만으로 특정 변수가 다른 변수에 미치는 영향을 정확하게 판단할 수 없음을 알 수 있다.
Causal Diagram Revisit
SCM으로부터 Casual Diagram을 만들 수 있다. 모든 variable에 대해 cause 관계를 그래프로 표현하면 아래 그림과 같다.
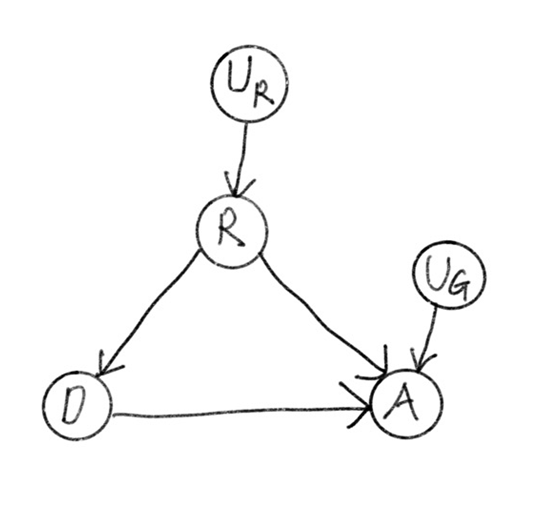
causal diagram을 만들 때 실제로는 $U_R, U_G$와 같은 unobservable한 확률변수는 나타내지 않기도 한다. 그러면 아래와 같이 diagram이 간단해진다.
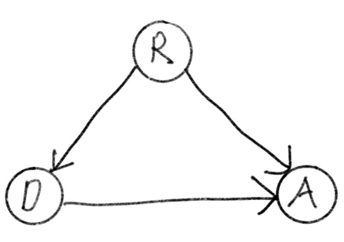
이 그림을 보면 introduction에서 소개했던 첫 번째 실험과 동일한 causal diagram이 나온다는 것을 알 수 있다.
즉, $R$이 $D$와 $A$의 cause이기 때문에 $D$가 $A$에 어떤 영향을 주는지 관찰하기 위해서는 $R = 1$인 경우와 $R = 0$인 경우를 나누어서 각각에 대해 통계를 내야 확인할 수 있다. 그러나 위에서는 $ P(A \mid D) = 1, P(A \mid \lnot D) = \frac{1}{2} $ 의 값으로만 판단했기 때문에 약이 전염병으로 인한 사망을 막는데 효과적이라는 잘못된 결과를 얻은 것이다.
SCM으로부터 만들어진 Causal Diagram은 Directed Acyclic Graph(DAG)라는 특성을 지닌다 (Cause 관계는 인과관계이므로 cycle이 없다고 가정할 수 있다). SCM을 정의할 때 도입한 $\textbf{pa}_i$ 는 이렇게 만들어진 DAG에서 $V_i$로 갈 수 있는 $V_j$들의 집합이다.
Conditional Independence
여기서는 Causal Diagram에서 condition된 variable들이 있을때 변수들이 독립인지 아닌지를 판단하는 기준에 대해 다룬다.
Definition 2(probabilistically independent). 확률변수 $X$와 $Y$에 대해, $X$의 값이 $x$라는 것을 아는 것이 $Y$의 확률분포에 아무 영향을 미치지 않는 경우 $X$와 $Y$가 서로 독립이라고 정의한다.
\[X \perp \!\!\! \perp Y \iff P(Y = y | X = x) = P(Y = y)\]
Definition 3(conditonally independent). 더 일반적으로, 확률변수 $Z$가 취할 수 있는 모든 값 $z$에 대해, $Z=z$임을 알고 있을 때 $X$와 $Y$가 서로 독립임이 성립하는 경우 $X$와 $Y$가 $Z$에 대해 conditionally independent 이라고 정의한다.
\[X \perp \!\!\! \perp Y | Z \iff P(Y = y | X = x, Z = z) = P(Y = y | Z = z)\]
이 정의는 $Z$가 하나의 확률변수가 아닌 확률변수들의 집합이 되어도 문제없이 확장 가능하다. \(Z = \{ Z_1, Z_2, .., Z_k \}\) 에 대해 $Z$의 값을 알고 있을 때 $X$와 $Y$가 서로 독립임이 성립하는 경우 $X, Y$는 $Z$에 대해 conditionally independent 하다.
Causal Digram and Conditional Independence
주어진 Causal Diagram에 대해서, 두 변수 $X, Y$가 independent인지 알 수 있는 방법이 있을까? 나아가, 변수 $X, Y, Z$ 에 대해 $X, Y$가 conditionally independent given $Z$인지 여부를 판단할 수 있을까?
Chains and Forks
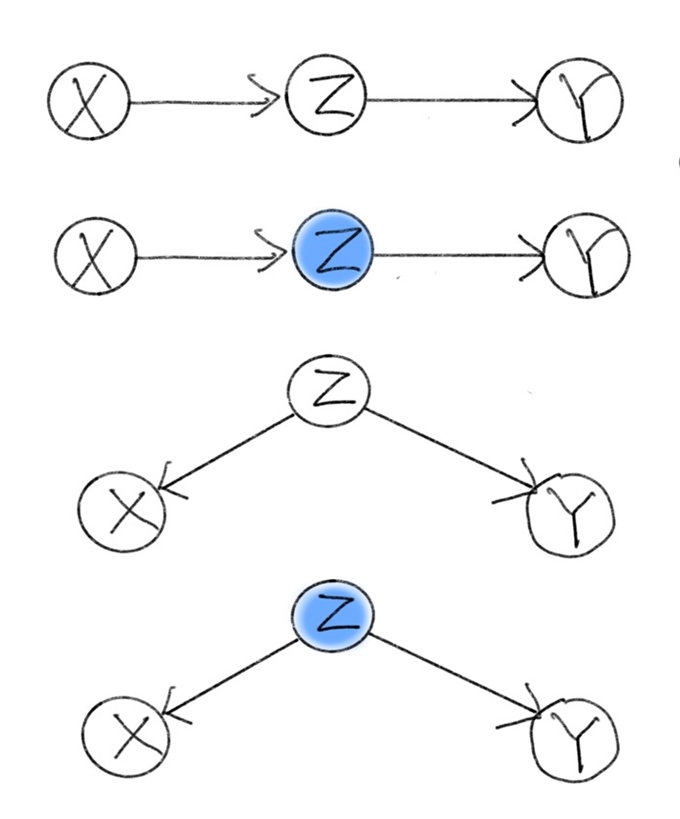
위 이미지의 첫 번째 Causal Diagram을 보자. vertex들이 체인처럼 연결되어 있어 이와 같은 모양을 chain이라 부른다. chain에서 $X$ 와 $Y$가 independent하지 않음은 쉽게 알 수 있다.
동일하게 chain인 두 번째 Diagram을 보자. 푸른색으로 칠해진 $Z$는 $Z$가 condition되었음을 뜻한다. $Z$에 대해 $X$와 $Y$는 conditionally independent할까?
\[P(x,y|z) = \frac{P(x,y,z)}{P(z)} = \frac{P(y|z)P(z|x)P(x)}{P(z)} = \frac{P(x,z)}{P(z)}P(y|z) = P(x|z)P(y|z)\]이므로, $X$ and $Y$ are independent given $Z$.
세 번째 Causal Diagram을 보자. $Z$가 $X$ 와 $Y$의 common cause인 경우이다.
$Z$가 감기에 걸린 상태를 나타내고, $X$가 고열이 나는 상태, $Y$가 콧물이 나는 상태를 나타내는 확률변수이면 해당 Causal Diagram과 매칭된다. 이 예시에서 $X$와 $Y$는 자명하게 independent하지 않다.
$Z$가 condition된 네 번째 Diagram을 보자. $Z$에 대해 $X$와 $Y$는 conditionally independent함을 다음과 같이 보일 수 있다.
\[P(x,y|z) = \frac{P(x,y,z)}{P(z)} = \frac{P(y|z)P(x|z)P(z)}{P(z)} = P(x|z)P(y|z)\]Chain과 Fork에서는 $X, Y$ 사이의 $Z$가 condition됨으로써 $X$와 $Y$가 independent하게 되므로, $Z$가 $X$와 $Y$를 block한다고 말한다.
Colliders
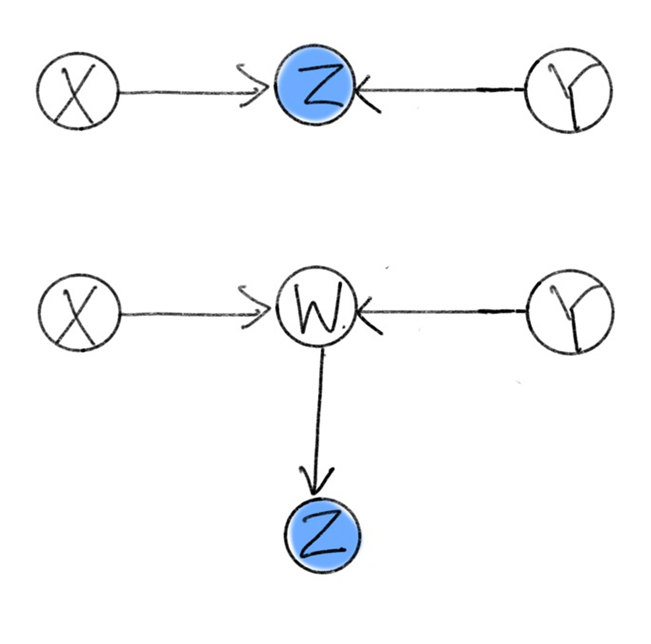
위 causal diagram들에서 $Z$가 conditioned되지 않았을 때, $X, Y$는 다른 변수들로부터 영향받지 않으므로 independent하다.
그러나 $Z$가 conditioned된 경우에는 $X, Y$가 서로 independent하지 않다. 이는 간단한 예시로 설명이 가능한데, 두 학생 (학생 1, 학생 2)가 교실에 있다고 생각하자. $X$는 학생 1이 김씨임을 나타내고, $Y$는 학생 2가 박씨임을 나타내며, $Z$가 학생 1이 김씨이고 또한 학생 2는 박씨임을 나타낸다면 $Z$가 참인 경우 $X$와 $Y$는 independent하지 않음을 쉽게 보일 수 있다.
마찬가지로, 중간에 다른 변수 $W$가 끼어 있더라도 $X$에서 $Z$로 가는 directed path가 존재하고, $Y$에서 $Z$로 가는 directed path가 존재하는 경우에 $Z$가 condition되면 $X$와 $Y$는 independent하지 않다.
Collider에서는 $Z$가 condition됨으로써 $X$와 $Y$ 사이에 연관관계가 생기게 되므로, $Z$가 $X$와 $Y$를 unblock한다고 말한다.
d-seperation
Causal Diagram $G = (V, E)$에서, $Z \subset V$가 conditioned된 상태라고 할 때 두 변수 $X, Y$가 conditionally independent given $Z$인지 어떻게 확인할 수 있을까?
각 edge를 undirected edge라고 생각했을 때 $X$와 $Y$를 잇는 모든 path를 생각해보자.
$ P = (p_1, p_2, .., p_k), p_1 = X, p_k = Y, ((p_i, p_{i+1}) \in E \lor (p_{i+1}, p_i) \in E) $ 가 성립하는 모든 $P$
만약 이 중 active path가 하나라도 있다면 $X$와 $Y$는 given $Z$에 대해 independent하지 않음이 알려져 있다.
path가 active하다는 것은 아래와 같이 정의된다.
path $(p_1, .., p_k)$ 에 대해 $(p_1, p_2, p_3), (p_2, p_3, p_4) , …, (p_{k-2},p_{k-1}, p_k)$의 triplet들을 생각 해 보자. 각 triplet $(A, B, C)$는 chain이거나(두 방향 모두 가능), fork이거나, collider일 것이다.
- chain이나 fork인 경우 $B$가 condition되어있지 않을 때 active triplet, 그렇지 않은 경우 inactive triplet이라 한다.
- collider인 경우 $B$의 descendent 중 condition된 variable이 존재할때 active triplet, 그렇지 않은 경우 inactive triplet이라 한다.
모든 triplet이 active triplet인 path만을 active path로 정의한다.
임의의 Causal Graph에서 $X, Y$ are conditionally independent given $Z$이면 $X, Y$를 잇는 active path는 존재하지 않는다. 그러나 그 역은 성립하지 않을 수 있다. 즉, conditionally dependent하지만 active path가 존재하지 않을 수도 있다.
하지만 대부분의 간단한 경우에서는 dependent할 때 active path를 찾을 수 있으며, active path를 찾아봄으로써 $X, Y$가 conditionally independent given Z인지 판단하는 과정을 d-seperation이라고 한다.
이때까지 살펴본 내용은 $X$와 $Y$가 확률변수 하나가 아닌 집합인 경우로 확장 가능하다. 즉, $X$의 원소 $V_i$와 $Y$의 원소 $V_j$ 사이의 active path가 존재하는지 찾는 과정을 반복하면 충분하다.
Causal Effect
Definition 3(Causal Effect). SCM $M = (V, U, F, P(U))$ 에서 $X, Y \subset V$가 서로소일 떄, $Y$에 대한 $X$의 causal effect, 또는 $P(y \mid do(x))$ 는 $X$로부터 $Y$의 확률분포의 공간으로의 함수이다. 이 값은 아래와 같이 얻어진다:
$X$의 realization $x$에 대해, $P(y \mid do(x))$의 값은 SCM $M$에서 $X$에 포함되는 모든 변수에 대한 $f_X$를 제거하고 $X=x$를 대입했을때 얻는 새로운 SCM $M’$에서의 $P(y)$로 정의된다.
Introduction의 첫 번째 예시에서, 회복에 대한 변수 $Y$와 투약에 대한 변수 $X$에 대해 $P(y \mid x)$을 보면 약이 효과가 없다는 잘못된 결과를 얻을 수 있다.
이는 $P(y \mid x)$가 $Y$의 $X$에 대한 Causal Effect를 정확히 반영하지 못하기 때문이다.
Causal Effect인 $P(y \mid do(x))$는 Causal Diagram으로 따지면 $X$로 들어오는 모든 directed edge를 제거한 그래프이므로, $X$에서는 outgoing edge만 존재한다. 따라서, 이는 $Y$의 $X$에 대한 Causal Effect를 온전히 반영한다.
즉, $Y$에 대해 $X$가 미치는 영향을 온전히 알고 싶다면 $P(y \mid do(x))$를 계산하여야 한다.
Example
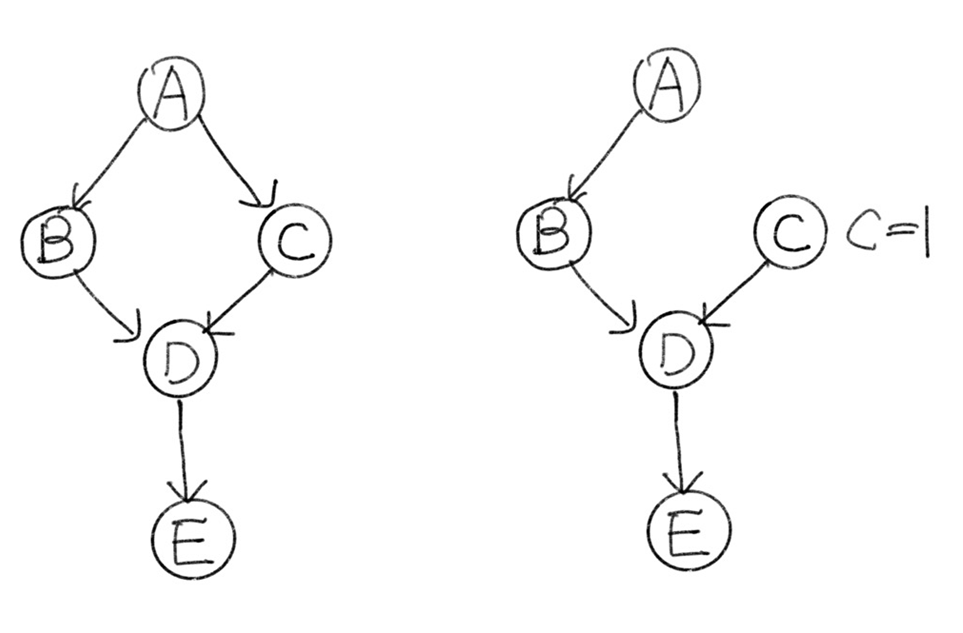
위 Causal Diagram에서, 각 variable $A, B, C, D, E$는 0 또는 1의 값을 가진다고 가정하자.
$P(d \mid do(c))$은 어떻게 계산할 수 있을까?
$P(d \mid do(C=1)) = \Sigma_{a, b} P(a)P(b \mid a)P(d \mid C=1,b) $
$P(d \mid do(C=0)) = \Sigma_{a, b} P(a)P(b \mid a)P(d \mid C=0,b) $
이므로 conditional probability를 통해 이를 계산할 수 있다.
Identification Problem & do-calculus
그러나 실제로 conditional probability $P(y \mid x) = \frac{P(x,y)}{P(x)}$가 많은 instance를 관찰함으로써 큰 수의 법칙을 통해 근사값을 쉽게 구할 수 있는 반면, $P(y \mid do(x))$의 값은 Causal Model을 알고 있더라도 구하기가 어렵거나 불가능할 수 있다.
심지어 동일한 $U, V$에 대해 정의된 두 SCM $M_1, M_2$에서 모든 $v$에 대해 $P(v)$가 동일할 때도 $P(y \mid do(x))$는 서로 다른 경우가 존재한다. 이럴 때는 SCM의 causal diagram $G$와 $P(V)$로도 $P(y \mid do(x))$가 정해지지 않아서 $Y$에 대한 $X$의 causal effect가 non-identifiable하다고 한다. 반대로 $P(y \mid do(x))$가 정해지는 경우에는 identifiable하다고 하고, 이를 결정하는 문제를 identification problem이라고 한다. 당연하게도, 통계로 얻을 수 있는 정보는 $P(V)$에 대한 값이기 때문에 이를 이용해 non-identifiable한 causal effect인 $P(y \mid do(x))$를 구하는 것은 불가능하다.
Identifiable한 Causal Effect의 경우에도 위에서 본 예처럼 간단하게 conditional probability를 통해 Causal Effect를 계산할 수 있는 경우는 많지 않다. 이를 위해 Backdoor Criterion, Adjustment Criterion과 같은 많은 방법들이 발표되었으며 결국 처음의 $P(y \mid do(x))$를 몇 개의 rule을 통하여 변형하여 모든 identifiable한 Causal Effect를 do-free한 expression으로 표현하는 방법인 do-calculus로 이에 대한 연구가 정리되었다.
Theorem 1 (completeness of do-calculus). The causal quantity $Q = P(y \mid do(x))$ is identifiable from $P(v)$ and $G$ if and only if there exists a sequence of application of the rules of do-calculus and the probability axioms that reduces $Q$ into a do-free expression
Causal Effect와 Causal Inference에 대한 내용에 좀더 흥미가 있는 독자들은 CAUSAL INFERENCE IN STATISTICS: A PRIMER 를 찾아보면 좋을 것이다.
결론
현재 세상은 유례없이 통계와 데이터로 넘치고 있지만 이를 올바르게 해석하는 것은 쉽지 않은 일임을 Introduction의 여러 예시를 통해 알 수 있다. 단순히 생각했을 때는 조건부 확률로도 인과관계를 설명할 수 있을 것처럼 보이지만 전염병의 예시를 통해 그것이 위험한 판단을 불러일으킬 수 있음을 보았다.
Causal Inference를 공부하는 것은 실험을 설계하고 얻은 통계로부터 어떠한 결론을 올바르게 도출할 수 있는지를 배우는 것임은 물론이고, 인과관계와 상관관계의 혼동성을 자신의 목적을 위해 교묘하게 이용하는 수많은 통계들에 속지 않도록 도와줄 수 있을 것이다.