Graph Distance Labeling Problem
Introduction
정점이 $N$개인 무방향 무가중치 그래프가 주어졌을 때, 아무 두 정점 $u, v$ 사이의 최단 경로의 길이를 질문(query)할 수 있는 자료구조를 만들고 싶다고 합시다.
일반적인 상황이라면 이 질문에 대한 답은 매우 간단합니다. Floyd-Warshall 알고리즘 등으로 정점의 최단 경로를 크기 $N \times N$ 배열 (lookup table) $d$에 저장하고, $d(u, v)$를 $O(1)$ 시간에 찾아주면 됩니다.
하지만 어떤 이유로 Lookup table $d$를 유지할 수 없다고 합시다. query time에 $d$를 접근하는 비용이 너무 큰 상황이나, 분산 네트워크 환경에서 중앙화된 lookup table의 안정성을 보장할 수 없는 상황등이 이에 해당합니다. 따라서, 각 정점 $v = 1, \cdots, N$에 적당히 binary string label $\ell(v)$를 붙여서, 두 정점 $u, v$의 거리 $d(u, v)$가 오직 label의 함수 $f$로만 계산되도록 해볼 수 있을까요? 즉 $d(u, v) = f(\ell(u), \ell(v))$가 성립해야 합니다.
갑자기 요구 조건이 까다로워졌지만, 전혀 어렵지 않게 바뀐 문제를 해결할 수 있습니다. Lookup table $d(\cdot, \cdot)$의 $i$번째 row $d(i, \cdot)$을 정점 $i$의 label $\ell(i)$로 삼으면 되기 때문입니다. $d(u, v)$를 구해야 한다면 역시 $\ell(u)$의 substring으로 저장된 $d(u, v)$를 상수 시간에 가져올 수 있습니다.
이 때 $\ell(i)$의 길이는 어느 정도가 될까요? $d(u, v) \le n$이니, 길이 $\log n$의 binary string으로 쓸 수 있습니다. 즉, $v = 1, \cdots, n$에 대해 $d(u, v)$를 이어붙인 label $\ell(u)$의 길이는 $\Theta (n \log n)$이 됩니다. 이 문제가 흥미로운 이유는 $\ell(u)$의 길이를 이보다 훨씬 줄일 수 있기 때문입니다.
이 글에서는 IOI 2010 Saveit의 풀이로도 유명한 Winkler(1983)의 $O(n)$ 방법과, 후속 연구 중 주목할 만한 Alstrup (2015), Gawrychowski (2016)을 리뷰합니다.
Notation fixing
글 전반에 걸쳐 자주 등장하는 개념의 표기법을 미리 정해둡시다.
Heavy-Light Decomposition (HLD)
정점이 $\lbrace 1, \cdots, n\rbrace$인 rooted tree $T$에 대해, $T$의 heavy-light decomposition $\mathcal{H} _ {T} = \lbrace (r _ {i}, S _ {i})\rbrace _ {i = 1}^{h}$ 를 정의합시다.
- 각 $S _ {i}$는 $\lbrace 1, \cdots, n\rbrace$의 부분집합으로 직선을 이루되, $r _ {i}$를 시조로 하는 조상-자손 관계를 이룹니다. 보통 $S _ {i}$를 “(heavy) chain”, $r _ {i}$를 “$S _ {i}$의 head”라고 부릅니다.
-
임의의 두 정점 $u, v$에 대해 두 점을 잇는 경로 위의 서로 다른 chain은 $O(\log n)$개입니다.
- $T$의 HLD $\mathcal{H} _ {T}$는 $O(n)$ 시간에 찾을 수 있습니다. 링크
Problem statement
Labeling
주어진 그래프 $G$에 대해서 label $(\ell(v)) _ {v = 1}^{N}$을 생성하는 과정을 labeling 이라고 합니다. Labeling step에서 시간 복잡도보다는 output label의 길이를 최소화하는 게 목적입니다. 주로 “maximum label length” $\mathrm{LMAX} _ {G} := \max _ {v} \lvert \ell(v) \rvert$ 또는 “total label length” $\mathrm{LTOT} _ {G} := \sum _ {v} \lvert \ell(v) \rvert$ 를 최소화하는 것이 목표입니다.
Decoding
두 정점 $u, v$가 쿼리로 주어졌을 때, $\mathrm{DECODER}(\ell(u), \ell(v)) = d(u, v)$를 계산하는 과정을 decoding 이라고 합니다. Decoding time을 feasible한 수준으로 유지하는 게 두 번째 우선순위라고 볼 수 있습니다.
General case, Specific graph class
몇 가지 그래프들의 모임 (graph class) 들을 다음과 같이 써봅시다.
- $\mathrm{Graph} _ {n}$ : 정점이 $n$개인 모든 무방향 연결그래프의 모임
- $\mathrm{Tree} _ {n}$ : 정점이 $n$개인 모든 트리의 모임
- $\mathrm{Planar} _ {n}$ : 정점이 $n$개인 모든 평면그래프의 모임
- $\mathrm{bTW} _ {n}$ : 정점이 $n$개인, 모든 bounded treewidth graph의 모임
- etc…
weighted인 경우는 weight의 범위를 나타내는 superscript $W$로 표기하겠습니다.
- $\mathrm{Planar} _ {n}^{W}$ : 정점이 $n$개이고, 간선의 weight가 $[0, W]$에 속하는 평면그래프의 모임
모든 $G \in \mathrm{Graph} _ {n}$에 대해 짧은 label이 존재하는 labeling scheme이 있다면 좋겠으나, 어떤 방법을 쓰더라도 $\mathrm{LMAX} = \Omega(n)$인 그래프가 존재한다는 것이 알려져 있습니다. (Gavoille 2004) 앞서 지나가듯 $\mathrm{LMAX} = O(n)$인 방법이 있다고 (Winkler 1983) 언급했기 때문에, 결국 $\mathrm{Graph} _ {n}$의 labeling과 관련된 문제는 $\mathrm{LMAX} = cn + o(n)$에서 계수 $c$, decoding 시간 복잡도, error term $\mathrm{LMAX} - cn = o(n)$ 등을 고려하여 optimality를 따지는 subtle한 문제가 됩니다.
반면 $\mathrm{Tree} _ {n}, \mathrm{Planar} _ {n}$처럼 간선의 개수가 $O(n)$인 graph class의 경우, $\mathrm{LMAX} = o(n)$인 sub-linear labeling을 갖습니다. 가장 간단한 트리의 예를 봅시다.
Proposition. $T \in \mathrm{Tree} _ {n}$일 때, $\mathrm{LMAX} _ {T} = O(\log^{2} n)$.
Proof. $T$의 루트 $r$을 고정하고, 정점의 heavy-light decomposition을 생각합시다. 각 정점 $v$에 대해 $r$에서 $v$로 내려오면서 거치게 되는 heavy chain $S _ {1}^{v}, \cdots, S _ {k}^{v}$의 head $r _ {1}^{v} (=r), \cdots, r _ {k}^{v}$를 구할 수 있는데, $\ell(v)$에 $2k$개의 수 $r _ {1}^{v}, d(r _ {1}^{v}, r _ {2}^{v}), r _ {2}^{v}, d(r _ {2}^{v}, r _ {3}^{v}), \cdots, r _ {k}^{v}, d(r _ {k}^{v}, v)$를 기록해줍니다. 이 때 $\ell(u), \ell(v)$가 주어지면 두 정보를 바탕으로 $u, v$의 LCA (Least Common Ancestor)를 구할 수 있고, $d(u, v)$를 $O(\log n)$ 시간에 계산할 수 있습니다.
$\ell(v)$의 길이를 생각하면 $k = O(\log n)$이고, 모든 수의 범위가 (unweighted tree 기준) $O(n)$이기 때문에 $\lvert \ell(u) \rvert = O(\log^{2} n)$입니다. $\square$
많은 graph class에 대해 label length의 upper bound 및 lower bound가 개별적으로 연구되어 있고, 대부분의 작은 class에서는 Gavoille (2004)에서 제시된 lower bound와 state-of-the art upper bound가 asymptotically tight한 것으로 알려져 있습니다. 다만 “Sparse graph”와 같이 graph class가 broad한 경우에는 많은 결과가 알려져 있지 않고, 이 중에서 최근에 진전이 있었던 unweighted planar graph의 경우를 알아봅니다.
$\mathrm{Graph} _ {n}$
Winkler (1983)
발상 당시에 $\mathrm{Graph} _ {n}$의 distance labeling problem이 지금과 같은 형태는 아니었습니다. Graham-Pollak (1972) 에서 제시한 형태는 다음과 같은 “isometry problem”에 가까웠습니다.
$0, 1, \ast$로 이루어진 길이가 같은 두 ternary string $S = s _ {1}\cdots s _ {l}, T = t _ {1}\cdots t _ {l}$를 생각해봅시다. $S, T$의 hamming distance $D _ {H}(S, T)$를 $\sum _ {i=1}^{l} f(s _ {i}, t _ {i})$로 정의합니다. 이 때 comparator $f(x, y)$는
$f(x, y) = \begin{cases} 1 & (\lbrace x, y\rbrace = \lbrace 0, 1\rbrace) \ 0 & (\text{otherwise})\end{cases}$
로 정의합니다. 즉 기존의 binary string에 대한 hamming distance에 모든 점과 거리가 $0$인 문자 $\ast$를 추가한 문자열입니다. $l$ 차원 공간에 그려진 모습 때문에 이 문자열들의 공간을 “squashed cube”라고도 부릅니다. 다음은 실제 $K _ {4}$를 3차원 squashed cube에 그린 모습입니다.
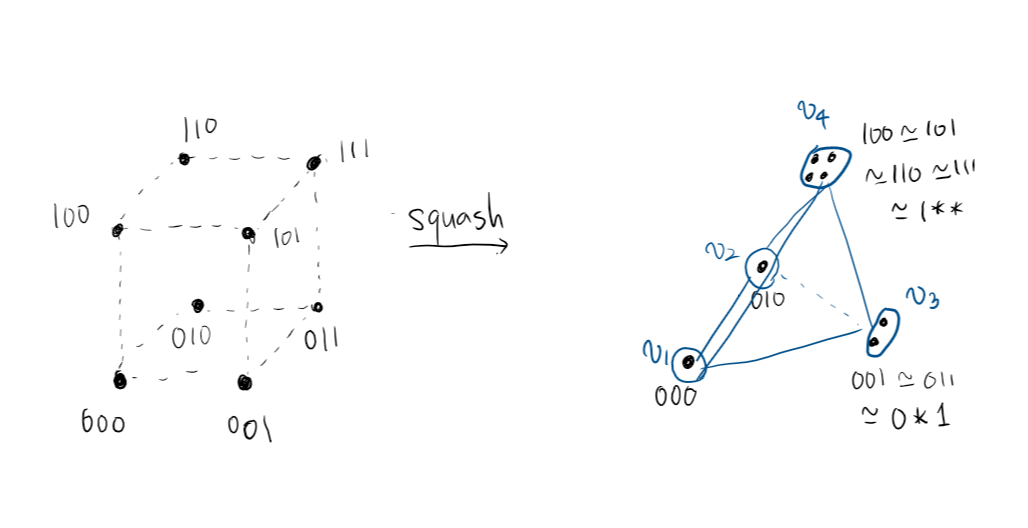
Problem (Squashed Cube Conjecture). $G \in \mathrm{Graph} _ {n}$이 주어졌을 때, $d(u, v) = D _ {H}(t(u), t(v))$인 ternary labeling $t$가 존재하는가? 존재한다면 $t$의 최소 길이는 얼마인가?
Graham-Pollak (1972, 이하 GP)에서는 $G = K _ {n}$일 때 $t$의 길이가 정확히 $n-1$이 필요하다는 결론을 얻었고, 이 과정에서 얻어진 것이 유명한 Graham-Pollak theorem입니다.
GP는 $t$의 길이가 $n-1$이면 충분하다고 생각했고, 실제로 Winkler (1983)이 이를 증명했습니다. 따라서 이 $t$를 기반으로 $\mathrm{Graph} _ {n}$의 labeling scheme을 만들 수 있고, $t$가 ternary string이니까 $\mathrm{LMAX} = \lceil (\log 3) (n-1) \rceil$을 얻습니다.
그래프의 아무 정점 $r$을 루트로 잡고, 그로부터 만들어지는 BFS tree (Shortest path tree) $T$를 생각합시다. 정점 $v \neq r$의 “부모 정점” $p(v)$를 생각하면, 아무 다른 점 $i$에 대해 $\lvert d(u, v) - d(u, p(v)) \rvert \le 1$이 성립하게 됩니다.
Exercise. 이 사실만을 이용하여 IOI Saveit을 해결할 수 있습니다. 약 $nh\log 3 + O(n \log n)$ 번의 encoding을 사용해보세요.
$c(u, v) := d _ {T}(u, v) - d(u, v) \ge 0$을 정의합시다. 위의 사실을 이용하면 아래와 같은 Lemma를 증명할 수 있습니다.
Lemma.
- $u, v$가 $T$에서 자손-조상 관계인 경우 $c(u, v) = 0$.
- 반면 $u, v$가 서로 다른 서브트리에 속하는 경우 $0 \le c(u, v) - c(u, p(v)) \le 2$.
$d(u, v) = d _ {T}(u, v) - c(u, v)$이므로, 다음과 같은 assignment $t$를 잘 분석하면 $D _ {H}(t(u), t(v)) = d(u, v)$가 되는 것을 알 수 있습니다. 증명은 지면 관계상 생략하겠습니다. 여기서 $t(i) _ {j}$ (코드의 t[i][j])는 $t(i)$의 $j$번째 문자를 의미합니다.
if j is ancestor of i:
t[i][j] = 1
elif c(i, j) - c(i, p(j)) == 2:
t[i][j] = *
elif c(i, j) - c(i, p(j)) == 1 and (i < j) == (c(i, j) % 2 == 0):
t[i][j] = *
else:
t[i][j] = 0
이 때 루트 $r$에 대해 항상 t[i][r] = 1이 되므로, 의미 없는 정보를 제거해주면 길이 $n-1$짜리 ternary label이 완성됩니다.
Alstrup (2015)
Winkler가 해결한 문제의 경우 decoding 방법이 “hamming distance on squashed cube”로 고정되어 있기 때문에 다소 작위적으로 느껴질 수 있습니다. 또한, 길이 $n \log 3$인 문자열의 hamming distance를 계산하는 데는 통상적으로 $O(n)$, bitset 등을 사용하여 $O(\log n)$ 길이의 문자열을 한 번에 처리할 수 있는 계산 모델에서는 $O(n / \log n)$ 의 시간이 필요하게 됩니다.
일반적인 distance labeling problem에 대해서는 이미 Naor (1988), Gavoille (2004) 등에 의해 $\mathrm{LMAX} \ge \frac{n}{2}$, $\mathrm{LSUM} \ge \frac{n^2}{2} + O(n \log n)$ 이 알려져 있었습니다. 따라서 leading term의 계수와 decoding time을 동시에 (혹은 둘 중 하나를) 줄이려는 시도가 있었고, 그 종착역은 Alstrup (2015) 이 선보인 $\mathrm{LMAX} = \frac{\log 3}{2} n + o(n)$과 $O(1)$ decoding time이었습니다.
Theorem. (Alstrup 2015) $G \in \mathrm{Graph} _ {n}^{W}$에 대해, $\mathrm{LMAX} \le \frac{1}{2}n \log(2W + 1) + O(\log n \cdot \log (nW))$.
$O(1)$ decoding time을 보장하기 위해서는 복잡한 parameter tuning이 필요합니다. 그 과정도 분명히 의미가 있지만, 여기서는 decoding time을 신경쓰지 않은 labeling scheme만 이야기하기로 합니다.
$G$의 shortest path tree를 $T$라 두고, $T$의 heavy-light decomposition 중 유명한 HLD를 잡아서 heavy-path 들이 dfs-ordering 상에서 연속한 구간을 차지하도록 합시다.
$\delta _ {x}(u, v) := d _ {G}(x, v) - d _ {G}(x, u)$라고 두면, 임의의 정점 $u, v$와 $z := \mathrm{LCA}(u, v)$에 대해
$d _ {G}(u, v) = d _ {T}(u, z) + \sum _ {x \in (z, v]} \delta _ {u}(p(x), x)$
가 성립하게 됩니다. 이 때 $(z, v]$는 $v$의 조상들 중 $z$보다 아래에 있는 모든 정점들을 말합니다. 이 정보들을 모두 $\ell(u)$에 담을 수 있다면 성공입니다.
LCA를 구하기 위한 자료구조로 각 정점 $v$에 대해 $v$의 부모 간선을 타고 올라가면서, 각 heavy chain과의 교집합 중 맨 윗점, 아랫점을 저장해 두고, 이 점들의 집합을 $\mathrm{hp}(v)$라고 둡시다. 또한 $\mathrm{hp}(v)$에 속한 점들과 $v$의 거리를 저장해 둡니다. 이를 $\mathrm{hpd}(v)$로 쓰겠습니다. 각각 $\lvert \mathrm{hp}(v) \rvert + \lvert \mathrm{hpd}(v) \rvert = O(\log n \cdot \log (nW))$입니다.
두 점 $u, v$가 조상-자손 관계라면 $\mathrm{hp}(u)$, $\mathrm{hp}(v)$가 포함관계를 갖습니다. 이 경우 $d _ {G}(u, v) = d _ {G}(v, r) - d _ {G}(u, r)$로 구할 수 있습니다. $d _ {G}(u, r) = d _ {T}(u, r) \in \mathrm{hpd}(u)$, $d _ {G}(v, r) \in \mathrm{hpd}(v)$임에 주목하세요.
두 점 $u, v$가 서로 다른 서브트리에 속하는 경우에는 상황이 약간 복잡해집니다. 이 경우 LCA $z$는 항상 $\mathrm{hp}(u) \cup \mathrm{hp}(v)$에 속하는 것을 알 수 있습니다.
$d _ {G}(u, v) = d _ {T}(u, z) + \sum _ {x \in (z, v]} \delta _ {u}(p(x), x)$
해당 식에서 $d _ {T}(u, z)$를 계산해봅시다.
- $z \in \mathrm{hp}(u)$인 경우 그냥 $d _ {T}(u, z) \in \mathrm{hpd}(u)$입니다.
- $z \in \mathrm{hp}(v)$인 경우, $d _ {T}(u, z) = d _ {T}(u, r) - (d _ {T}(v, r) - d _ {T}(v, z))$ 로 계산할 수 있습니다.
따라서 $x \in (z, v]$에 대해 $\delta _ {u}(p(x), x)$를 $\ell(u)$가 모두 들고 있기만 하면 충분합니다. 이 때 정점 $x$의 dfs order (on $T$)를 $\mathrm{dfs}(x) \in \lbrace 0, \cdots, n-1\rbrace$라고 두면, $\mathrm{dfs}(x) \in (\mathrm{dfs}(u), \mathrm{dfs}(u) + \frac{n}{2}]$에 대해서만 $\delta _ {u}(p(x), x)$의 값을 저장해두면 충분합니다. 이 때 $\mathrm{dfs}(u) \ge n/2$이면 circular하게 생각하여 $(\mathrm{dfs}(u), n-1] \cup [0, \mathrm{dfs}(u) - n/2]$의 범위를 저장합니다. 이 데이터를 $\Delta _ {u}$라고 하겠습니다.
일반성을 잃지 않고 $\mathrm{dfs}(u) < \mathrm{dfs}(v)$라고 하면 모든 $x \in (z, v]$에 대해 $\mathrm{dfs}(x) \in [\mathrm{dfs}(u) + 1, \mathrm{dfs}(v) - 1]$입니다. 따라서 모든 $\delta _ {u}(p(x), x)$값이 $\Delta _ {u}$에 들어가거나, $\delta _ {v}(p(x), x)$가 $\Delta _ {v}$에 들어가게 됩니다. 두 경우 모두 $d _ {G}(u, v)$를 계산하는 데 문제가 없습니다. 후자의 경우에 식을 $v$ 기준으로 다시 쓰면 되기 때문이죠.
또 $\mathrm{hp}(v)$의 정점들을 mere index 대신 dfs order로 저장하면, dfs-order 기준으로 값을 저장해둔 $\Delta _ {u}$에서 $(z, v]$의 $\delta _ {u}$값을 access할 수 있습니다.
따라서 $\lvert \Delta _ {u} \rvert \le \frac{1}{2}n \log (2W + 1)$ ($\because \delta _ {u} (\ast, \ast) \in [-W, W]$)이므로 $\Delta _ {u}, \mathrm{hp}(u), \mathrm{hpd}(u)$를 모두 합쳐서 $\ell(u)$를 desired length 범위 안에 들어오도록 할 수 있습니다.
$\mathrm{Planar} _ {n}$
Well-separated property of planar graphs
Distance labeling에서 뜬금없이 Planar graph가 나오는 게 이상할 수 있습니다. Planar graph에서 graph distance labeling이 tractible한 가장 큰 이유는 Lipton and Tarjan (1980) 의 monumental한 정리입니다.
Theorem. $G \in \mathrm{Planar} _ {n}$에 대해, 합이 $1$인 non-negative vertex weight가 주어져 있다고 하자. 이 때 $\lvert S \rvert \le 2\sqrt{2n}$인 정점 집합 $S$가 존재하여, $G - S$의 모든 connected component의 weight sum이 $2/3$ 이하가 되도록 할 수 있다.
또한, 이러한 $S$를 linear time에 찾을 수 있다.
Weight를 균등하게 $\frac{1}{n}$으로 줄 경우, $S$는 $G - S$의 연결 컴포넌트 크기가 $\frac{2n}{3}$ 이하가 되도록 하는 separator입니다. 이렇듯 $G - S$의 연결 컴포넌트 크기가 $2n/3$ 이하인 $S$가 존재한다면 $S$를 $G$의 $\lvert S \rvert$-separator라고 부릅니다.
- 트리는 $1$-separator (centroid) 를 갖습니다.
- 앞서 보았듯, 평면그래프는 $O(\sqrt{n})$-separator를 갖습니다.
- 아쉽게도, sparsity (간선 개수가 $O(n)$) 만으로는 $o(n)$-separator가 존재하는 것을 보장할 수 없습니다. (Erdos, Szemerdi)
이러한 sublinear-separator property 덕에, $O(\sqrt{n} \log n)$ labeling scheme을 바로 만들 수 있습니다.
$G$의 separator $S$를 잡고, $G _ {1}, \cdots, G _ {k}$를 $G - S$의 connected component라고 합시다. 이 때
- $v \in G _ {i}$이면, $\ell _ {G}(v) = \ell _ {G _ {i}}(v) + \lbrace d(v, u) : u \in S\rbrace$
- $v \in S$이면, $\ell _ {G}(v) = \lbrace d(v, u) : u \in S\rbrace$
와 같이 recursive하게 만들어 주면
- $u, v \in G _ {i}$ : $\ell _ {G _ i}(u)$, $\ell _ {G _ i}(v)$를 이용하여 재귀적으로 계산
- $u, v \in S$ : trivial
- $u \in G _ {i}, v \in S$ : trivial
- $u \in G _ {i}, v \in G _ {j}$ for $i \neq j$ : $\min _ {x \in S} d(u, x) + d(v, x)$를 계산
하는 방법으로 decoding이 가능합니다. 물론 separator를 이용한 decomposition tree를 추가로 저장해주어야 하지만, leading order가 아니니 무시할 수 있습니다. label의 최대 크기는 $O(\log n) \cdot (\sqrt{n} + \sqrt{2n/3} + \cdots) = O(\sqrt{n} \log n)$이 되고, weighted planar graph의 경우에도 $W = O(n^{k})$를 가정하면 $O(\sqrt{n} \log n)$ sized label을 유지할 수 있습니다. (Gavoille, 2004)
Gawrychowski (2016)
Abboud (2011)에 의해, $G \in \mathrm{Planar} _ {n}^{O(n^k)}$인 경우 $\mathrm{LMAX} = \Omega(\sqrt{n} \log n)$이 성립하는 것으로 알려졌습니다. 다만 Unweighted의 경우 알려진 최선의 lower bound는 $\mathrm{LMAX} = \Omega(n^{1/3})$ (Gavoille 2004)로, upper bound와는 거리가 있었습니다.
Gawrychowski (2016)에서는 이 bound를 $O(\sqrt{n})$으로 발전시켰습니다. Logarithmic enhancement이긴 하지만, 사용하는 배경 지식이 흥미로워 소개합니다.
Simple cycle separator
Separator $S$가 simple cycle 형태면 큰 장점이 있는데, $S = \lbrace (u _ {0} = u _ {n}), u _ {1}, \cdots, u _ {n}, (u _ {n+1} = u _ {1})\rbrace$으로 쓰면 모든 정점 $v$에 대해 $\lvert d(v, u _ {i}) - d(v, u _ {i+1}) \rvert \le 1$이 성립하기 때문입니다. 따라서 $d(v, u _ {i})$ 대신 그 변화량을 저장하면 $O(\sqrt{n})$ 길이의 label을 만들 수 있습니다.
하지만 모든 평면그래프에 simple cycle separator가 존재하지는 않습니다. 당장 outer face 하나만 있는 트리를 생각할 수 있습니다. 다행히도, $2$-connected planar graph에는 비슷한 정리가 성립하는 것이 알려져 있습니다. $2$-connected graph란 아무 정점을 하나 제거해도 connectivity가 유지되는 그래프를 말합니다. 모든 Simple cycle은 $2$-connected입니다.
Theorem (Miller, 1983) $G \in \mathrm{Planar} _ {n}$이 $2$-connected이고, $G$의 face가 모두 $f$각형 이하라고 하자. 이 때 길이가 $2 \sqrt{2 \lfloor f / 2 \rfloor n}$ 이하인 simple cycle separator $S$를 $O(n)$ 시간에 찾을 수 있다.
즉, 우리는 기존의 그래프에 정점과 간선을 더해 triangulation한 그래프 $G’$을 찾고, Miller’s theorem을 사용하여 $G’$의 simple cycle separator $S’$을 찾습니다. 이 때 $S = V(G) \cap S’$ 역시 $G$의 separator가 됩니다. 물론 $S$는 simple cycle이 아니지만, $\lvert d(v, u _ {i}) - d(v, u _ {i+1}) \rvert \le d(u _ {i}, u _ {i+1})$가 작게 유지되기만 하면 됩니다.
Theorem (Gawrychowski, 2016) $G \in \mathrm{Planar} _ {n}$에 대해, $\sum _ {i} \log d(u _ {i}, u _ {i+1}) = O(\sqrt{n}))$인 separator $S = \lbrace u _ {1}, \cdots, u _ {n}\rbrace$이 존재한다.
이 정리가 주어져 있으면 $\mathrm{Planar} _ {n}$의 distance labeling problem이 해결되는 것은 명백합니다. 위 정리를 증명하는 것으로 글을 마치겠습니다.
Proof of Gawrychowski’s theorem
크기가 $k$인 cycle을 $C _ {s}$라고 할 때, $C _ {s}$의 “subdivision” $D _ {s}$를 다음과 같이 정의합니다.
- $D _ {3} = C _ {3}$, $D _ {4} = C _ {4}$.
- $k \ge 5$에 대해, $C _ {s} = (v _ {1}, \cdots, v _ {k})$에 대해 $\lceil k / 2 \rceil$ 개의 auxiliary node $T = (u _ {1}, \cdots, u _ {\lceil k / 2 \rceil})$을 추가한다. $v _ {i}$와 $u _ {\lceil i / 2 \rceil}$을 연결하고, $T$로 다시 recursive하게 $D _ {\lceil k / 2 \rceil}$을 만든다.
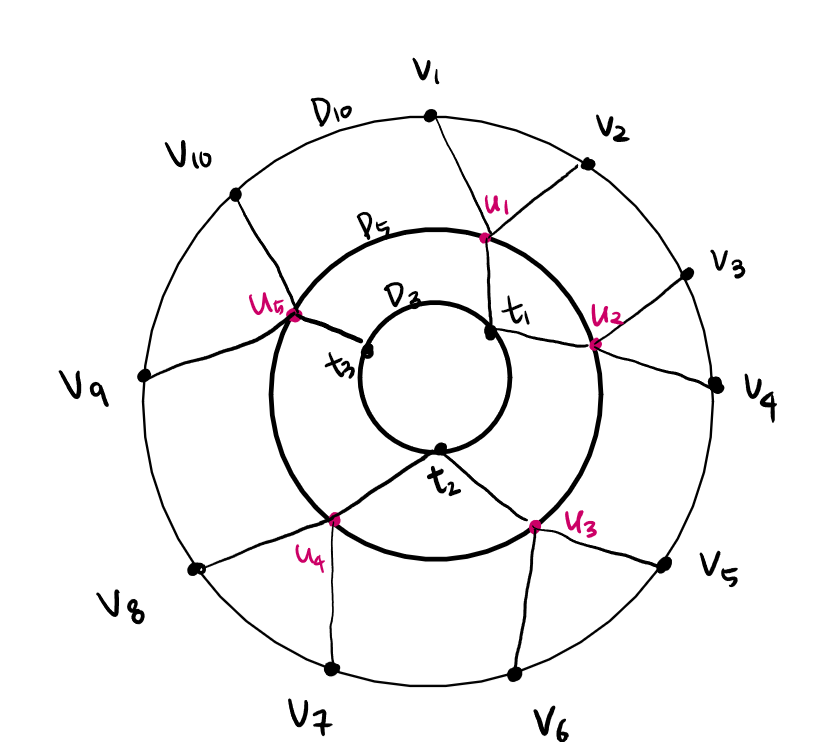
$C _ {s}$가 simple cycle일 필요는 없고, 단지 face이기만 해도 $D _ {s}$ 역시 평면그래프가 되도록 정점을 잘 추가할 수 있습니다. 또한 $D _ {s}$의 크기는 $2s$를 넘지 않습니다.
Lemma. 임의의 $u, v \in C _ {s}$에 대해, $d _ {D _ s}(u, v) \ge \log(1 + d _ {C _ s}(u, v))$.
Proof of lemma. $s \ge 5$에 대한 귀납법과, $D _ {s}$를 고정하고 $d = d _ {C _ s}(u, v)$에 대한 귀납법을 차례로 사용합니다. $d \le 2$인 경우에는 정리가 성립하므로 $d \ge 3$이라고 가정합시다.
$u, v$를 잇는 최단경로의 중간 점 ($u, v$ 자신을 제외한 점들)이 모두 $D _ {s} \backslash C _ {s}$ 위에 있다면 이 경로를 “special path”라고 합시다.
$\begin{aligned}d _ {D _ s}(u, v) &= 2 + d _ {D _ {\lceil s / 2 \rceil}}(u’, v’) \&\ge 2 + \log(1 + d _ {C _ {\lceil s / 2 \rceil}(u’, v’)})
&\ge 2 + \log(1 + \lfloor d / 2 \rfloor)
&\ge \log (1 + d)\end{aligned}$
가 되어 정리가 성립합니다. 다른 경우는 special path 여러 개의 concatenation으로 주어지므로, 사실상 $a _ {i} \ge \log(1 + b _ {i})$라면 $\sum _ {i} a _ {i} \ge \log(1 + \sum _ {i} b _ {i})$ 를 보이는 것으로 생각할 수 있습니다. $a _ {i}, b _ {i} \ge 1$에서 해당 부등식은 성립합니다. $\square$
이를 바탕으로 Gawrychowski’s theorem을 증명해봅시다.
Outer face를 포함한 $G$의 모든 face를 subdivide한 그래프 $G’$을 만듭시다. 이 때 각 간선은 $G’$의 새 정점을 만드는 데 최대 $2$번 기여할 수 있으므로, $\lvert V(G’) \rvert \le n + 2 \cdot (3n - 6) < 7n$입니다.
$G’$의 모든 face는 최대 사각형이므로, Miller’s theorem에 의해 크기가 $2\sqrt{28n} = O(\sqrt{n})$인 simple cycle separator $S’$이 존재합니다. $S = (S’ \cap V(G)) = (u _ {1}, \cdots, u _ {k})$라고 합시다. Ordering은 $S’$의 cycle order를 따릅니다.
$u _ {i}, u _ {i+1}$은 같은 $D _ {s}$ 위에 있어야 하므로, 두 점은 $G$의 같은 face에 인접합니다. 이 때 Lemma에 의해
$\begin{aligned} \sum \log d _ {G}(u _ {i}, u _ {i+1}) & \le \sum \log (1 + d _ {G}(u _ {i}, u _ {i+1}))
&\le \sum d _ {G’}(u _ {i}, u _ {i+1})
&\le \lvert S’ \rvert = O(\sqrt{n})\end{aligned}$
이 되어 원하는 바를 증명할 수 있습니다. $\square$
What’s left?
Distance labeling은 사실 굉장히 많은 정보를 담고 있습니다. Unweighted graph에서는 query만으로 adjacency relation을 모두 복구할 수 있기 때문에, label length를 polynomial bound 아래로 떨어뜨리기 아주 어렵습니다. 최근 연구인 Natan (2022)의 요약에 의하면, 다음 category가 활발하게 연구되고 있는 듯합니다.
- Approximate distance labeling: Constant factor로 근사할 수 있는 distance labeling을 구하는 문제입니다.
- Forbidden set distance labeling: source $s$, sink $t$, 그리고 “지나면 안되는 정점” $F$의 label들이 주어졌을 때 $F$-avoiding shortest path를 구하는 문제입니다.
References
General info
- Natan 2022 Aviv Bar-Natan, Panagiotis Charalampopoulos, Paweł Gawrychowski, Shay Mozes, Oren Weimann, Fault-Tolerant Distance Labeling for Planar Graphs, Theoretical Computer Science, 2022
Main papers
- Gawrychowski 2016 Paweł Gawrychowski and Przemys law Uzna´nski. A note on distance labeling in planar graphs. CoRR, abs/1611.06529, 2016.
- Alstrup 2015 Stephen Alstrup, Cyril Gavoille, Esben Bistrup Halvorsen, Holger Petersen: Simpler, faster and shorter labels for distances in graphs. SODA 2016: 338-350
- Gavoille 2004 Cyril Gavoille, David Peleg, St´ephane P´erennes, and Ran Raz. Distance labeling in graphs. Journal of Algorithms, 53(1):85–112, 2004
- Winkler 1983 Winkler, P.M. Proof of the squashed cube conjecture. Combinatorica 3, 135–139 (1983).
- Graham 1972 R. L. Graham and H. O. Pollak. On embedding graphs in squashed cubes. In Y. Alavi, D. R. Lick, and A. T. White, editors, Graph Theory and Applications, pages 99–110, Berlin, Heidelberg, 1972. Springer Berlin Heidelberg
Planar separator theorem
- Miller 1983 G. L. Miller, Finding small simple cycle separators for 2-connected planar graphs, J. Comput. Syst. Sci. 32 (3) (1986) 265 – 279
- Lipton 1980 R. J. Lipton, R. E. Tarjan, Applications of a planar separator theorem, SIAM J. Comput. 9 (3) (1980) 615–627