라틴 직사각형과 홀의 결혼 정리
라틴 방진과 스도쿠
라틴 방진 (Latin Square)은 서로 다른 $n$가지 기호로 구성되며, 각 행과 열에 $n$가지 기호가 모두 한 번씩 등장하게 만든 $n\times n$ 행렬입니다. 편의를 위해 $n$가지 기호 대신 $1$부터 $n$까지의 수 배열이라고 생각합시다.
라틴 방진을 만드는 방법은 여러 가지가 있는데, 가장 간단하게 생각할 수 있는 방법은 다음과 같습니다.
- 첫 번째 행에 $1$부터 $n$까지의 수를 순서대로 적는다.
- $k$번째 행에는 $k-1$번째 행을 왼쪽으로 한 칸 회전한 배열을 적는다. $(2 ≤ k ≤ n)$
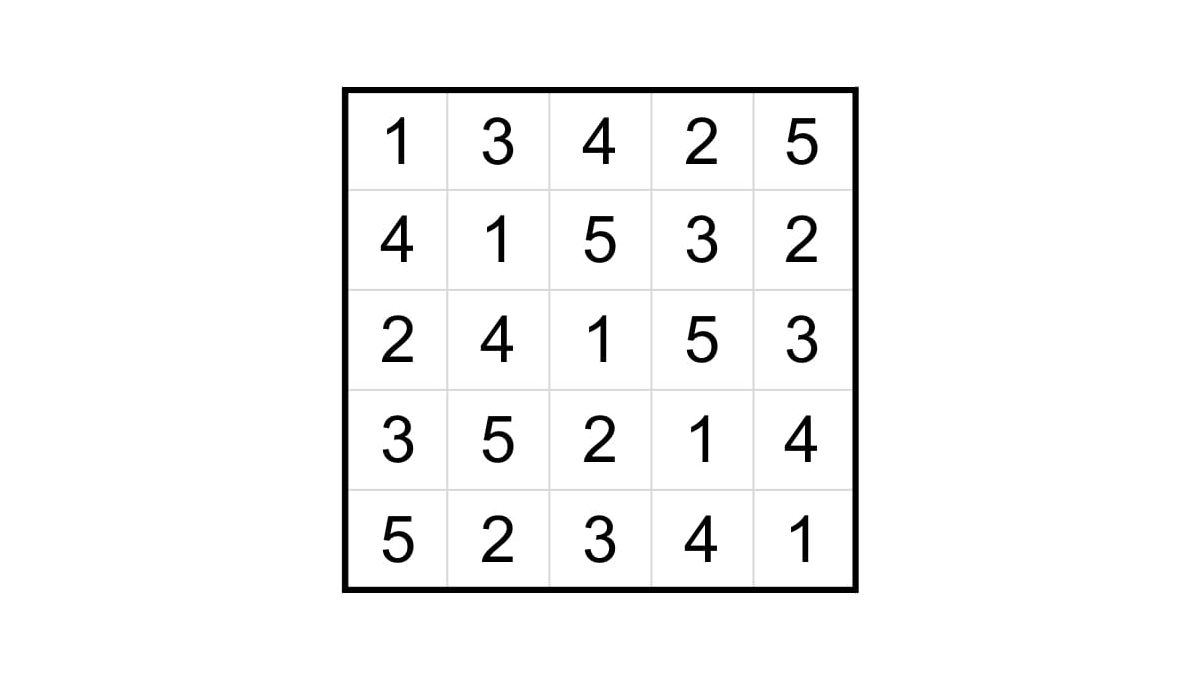
왼쪽으로 한 칸 회전한다는 것은 가장 왼쪽의 수를 가장 오른쪽으로 옮기는 것을 의미하며, 가령 첫 번째 행을 왼쪽으로 한 칸 회전하고 나면 $2, 3, \cdots, n, 1$ 이 됩니다. 회전을 반복해서 $n$개의 행을 모두 채우면 다음 그림과 같은 라틴 방진이 만들어집니다.
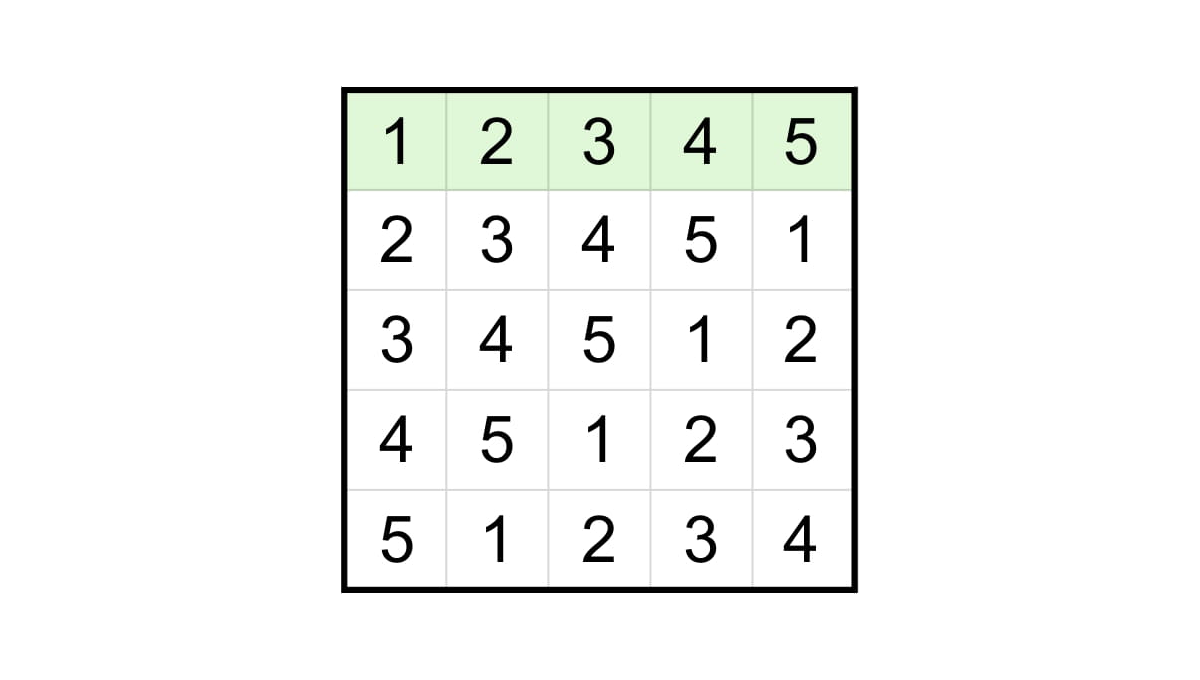
스도쿠를 풀어 본 적이 있는 독자라면 라틴 방진의 규칙이 스도쿠와 비슷하다는 것을 눈치챘을 것입니다. 스도쿠에서 $3\times 3$ 부분격자에 대한 조건을 없애면 $9\times 9$ 라틴 방진의 정의와 같아집니다.
스도쿠 문제를 풀때, 아무 숫자나 추측해서 채워 넣다 보면 더 이상 빈칸을 채워넣지 못하는 상황이 만들어지기 마련입니다. 아무렇게나 숫자를 채우는 것이 아니라 논리적 추론을 바탕으로 한칸 한칸 어떤 숫자가 들어가야 하는지 도출해야 스도쿠를 풀 수 있죠. 스도쿠가 퍼즐로서 성립하는 이유라고 할 수 있습니다.
라틴 방진도 마찬가지입니다. 아무 순서로 기호를 채워넣는다고 해서 라틴 방진을 만들 수 있는 것은 아닙니다. 각 행과 열에 중복된 기호가 없도록 행렬의 일부를 채웠다고 해도, 나머지 칸을 채워서 라틴 방진을 만들지 못하는 경우도 있습니다. 예를 들면 아래와 같은 경우입니다. 1행과 2행 모두 3열에 숫자 3을 채워 넣어야 하는데, 그러면 3열에서 중복이 생깁니다.
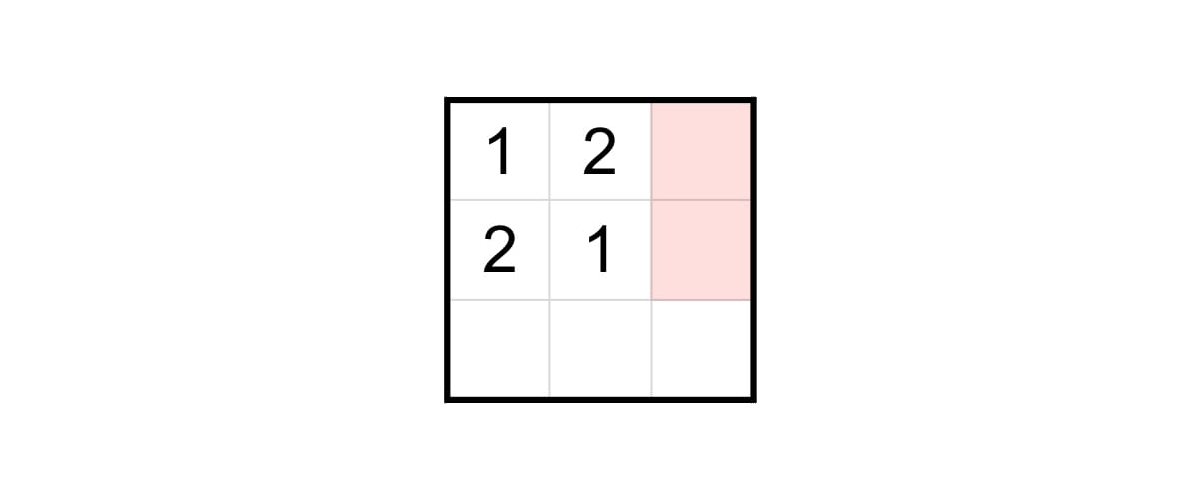
이렇게 $n\times n$ 행렬에서 각 행과 열에 중복이 없게 일부 칸을 채운 것을 부분 라틴 방진 (Partial Latin Square)이라고 부르겠습니다. 그러면 자연스럽게 다음과 같은 의문이 듭니다. 주어진 부분 라틴 방진의 빈 칸을 채워서 라틴 방진을 만들 수 있기 위해서는, 부분 라틴 방진이 어떤 조건을 만족해야 할까요? 이번 글에서는 이러한 조건의 예시 중 하나인 라틴 직사각형에 대해 알아보겠습니다.
라틴 직사각형
라틴 직사각형이란 서로 다른 $n$가지 기호로 구성되며, 각 행과 열에 중복되는 기호가 등장하지 않는 $r\times n\ (r ≤ n)$ 행렬입니다. 라틴 방진을 한 행 한 행씩 추가하며 만들다가 $r$개 행만 채우고 그만 둔 상태라고도 볼 수 있습니다.
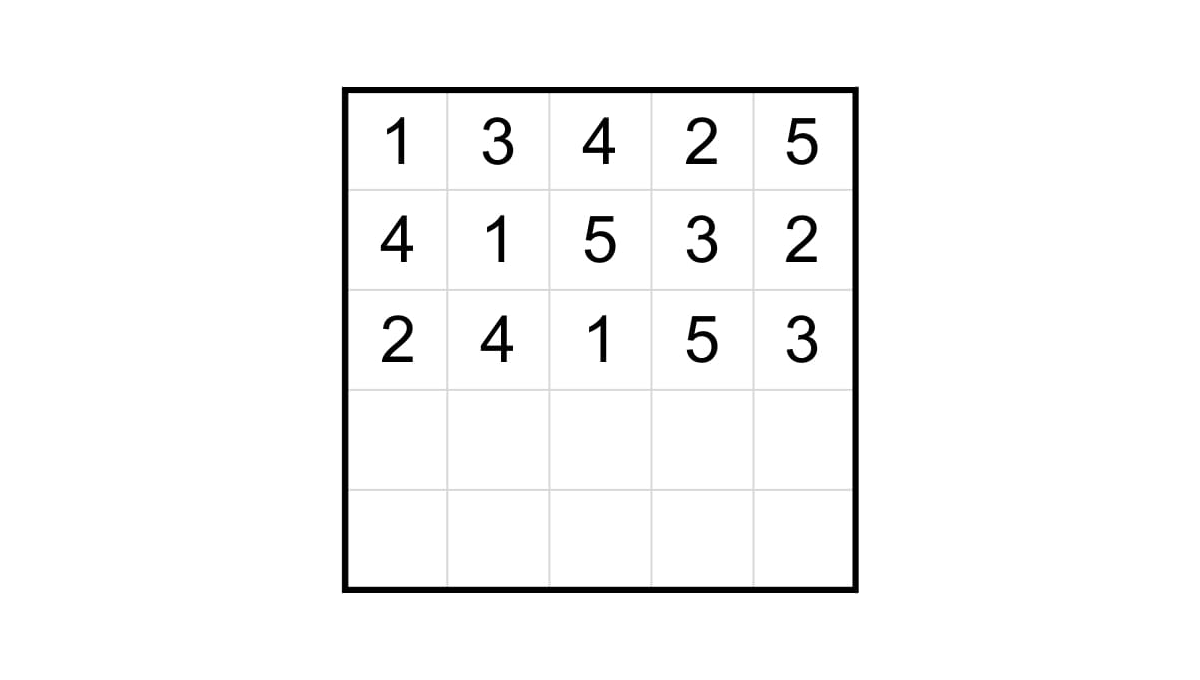
그렇다면 나머지 $n-r$개의 행을 추가해서 $n\times n$ 라틴 방진을 만들 수 있을까요? 비록 직사각형이라는 정돈된 형태를 갖추고 있긴 하지만, 결국 $r$개의 행은 아무렇게나 채운 것이기 때문에 왠지 라틴 방진을 완성하지 못하는 라틴 직사각형이 존재할 것 같습니다. 하지만 놀랍게도, 어떤 $r\times n$ 라틴 직사각형이 주어지든 항상 $n\times n$ 라틴 방진으로 확장하는 것이 가능합니다!
라틴 직사각형을 라틴 방진으로 확장 가능하다는 사실은, 임의의 $r\ (0 ≤ r < n)$에 대해 $r\times n$ 라틴 직사각형에 한 행을 추가해서 $(r+1)\times n$ 라틴 직사각형으로 확장 가능하다는 명제와 동치입니다. $r\times n$ 라틴 직사각형에 한 행을 추가하는 과정을 반복하면 $n\times n$ 라틴 방진을 만들 수 있고, 반대로 확장된 $n\times n$ 라틴 방진에서 첫 $r+1$개 행만 택하면 $(r+1)\times n$ 라틴 직사각형이 되기 때문이죠.
그럼 이제 $r\times n$ 라틴 직사각형에 행 하나를 추가하는 게 항상 가능하다는 것을 보일 차례입니다. 이를 위해서는 그래프 이론의 도움이 필요합니다.
이분 매칭 문제로의 변형
$n\times n$ 행렬 $A$의 첫 $r$개 행이 미리 채워져 있고, $r+1$번째 행을 채울 차례라고 합시다. 각 행과 열에 중복이 없어야 한다는 조건을 식으로 표현하면 다음과 같습니다.
- 행 중복 없음: $a_{(r+1)1}, \cdots, a_{(r+1)n}$은 서로 다르다.
- 열 중복 없음: $a_{(r+1)j}$에 들어갈 수 있는 수의 집합은 $\{1,\cdots, n\} \setminus \{a_{1j}, \cdots, a_{rj}\}$ 이다.
각 변수를 하나의 정점으로, 각 수를 또 다른 정점으로 만들어서 대응될 수 있는 변수와 값끼리 간선으로 이으면 이분 그래프가 만들어집니다. 변수마다 서로 다른 수를 배정해야 한다는 조건까지 더하면 이 그래프에서 완벽 이분 매칭 (Perfect Bipartite Matching)을 찾는 문제가 됩니다. 아래 그림은 라틴 직사각형과 이에 대응되는 이분 그래프, 그리고 $r+1$행에 대응되는 이분 매칭을 나타낸 예시입니다.
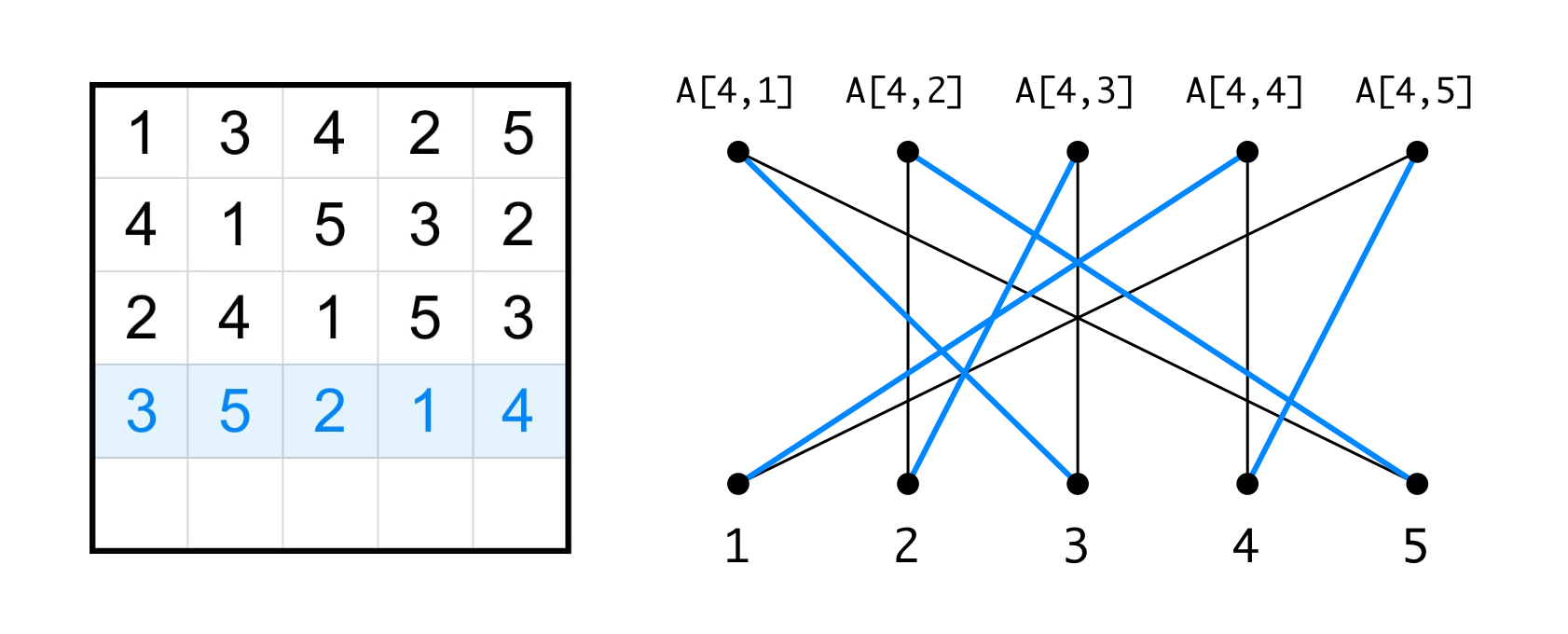
그런데 이렇게 만든 이분 그래프에는 중요한 특징이 하나 있습니다. 바로 모든 정점의 차수가 $n-r$로 같다는 점입니다. 각 변수에 들어갈 수 있는 값은 $n-r$가지이고, 각 수가 위치할 수 있는 열의 개수 또한 $n-r$개이기 때문입니다.
이렇게 모든 정점의 차수가 같은 그래프를 정규 그래프 (Regular Graph)라고 합니다. 우리가 만든 그래프가 이분 그래프라는 사실과 정점의 차수 $n-r$까지 붙이면 “$(n-r)$-정규 이분 그래프”라고 부를 수 있겠죠. 이제 다음 보조정리를 보이면 항상 $r+1$번째 행을 채울 수 있다는 사실을 증명할 수 있습니다.
Lemma 1. $k$-정규 이분 그래프는 항상 완벽 매칭을 갖는다.
이 보조정리를 증명하기 위해 먼저 홀의 결혼 정리를 알아봅시다.
홀의 결혼 정리
홀의 결혼 정리 (Hall’s Marriage Theorem)는 어떤 이분 그래프가 완벽 이분 매칭을 가질 필요충분조건을 나타낸 정리입니다.
Theorem 1. (Hall’s Marriage Theorem) $G$가 정점 집합 $X, Y$로 구성된 이분 그래프라고 하자. $X$의 부분 집합 $S$에 대해, $S$에 속한 정점에 이웃한 정점 집합을 $N_G(S)$라고 표기하자. $X$의 모든 정점을 커버하는 매칭을 $X$-완벽 매칭이라고 할 때, $X$-완벽 매칭이 존재하기 위한 필요충분조건은 다음과 같다.
모든 $S \subseteq X$에 대해,
\[\vert S\vert \leq \vert N_G(S)\vert\]이다. (홀의 조건, Hall’s Condition)
이 글의 흐름상 홀의 정리의 증명은 중요하지 않으므로 이해하지 않고 넘어가도 괜찮습니다.
홀의 정리를 증명하기 위해서는 두 가지 방향을 보여야 합니다.
$(\Rightarrow)$ 먼저, $X$-완벽 매칭이 존재할 때 홀의 조건이 성립하는 것은 자명합니다. $S$에서 매칭을 통해 연결된 정점들만 세어도 $\vert S\vert$개가 되니까요.
$(\Leftarrow)$ 반대 방향, 즉 홀의 조건이 성립하면 $X$-완벽 매칭이 존재한다는 사실을 보이는 과정은 보다 까다롭습니다. 여러 가지 증명 방법이 있지만, 여기서는 수학적 귀납법을 이용한 증명을 소개하겠습니다.
다음과 같이 $n = \vert X\vert$에 대해 강한 수학적 귀납법을 적용합니다.
기초 단계 (Basis Step): $n = 1$일 때, $\vert N_G(X)\vert \geq \vert X\vert = 1$ 이므로 $X$의 유일한 원소는 하나 이상의 $Y$의 원소와 연결되어 있습니다. 따라서 크기 1인 매칭을 찾을 수 있습니다.
귀납 가정 (Inductive Hypothesis): 모든 $1\leq k\leq n$에 대해, $\vert X\vert = k$일 때 홀의 정리가 성립한다고 가정합시다.
귀납 단계 (Inductive Step): 다음과 같이 두 가지 경우로 나누어 해결할 수 있습니다.
1) 공집합이 아닌 모든 진부분집합 $S \subset X$에 대해, $\vert S\vert < \vert N_G(S)\vert$가 성립하는 경우
아무 간선이나 하나 선택해서 매칭에 넣고, 양 끝 정점을 제거한 그래프 $G’(X’, Y’, E’)$을 생각합니다. 임의의 부분집합 $S\subseteq X’$에 대해서, $N_{G’}(S)$은 기존 $N_G(S)$에 비해 크기가 최대 1만큼 줄어들기 때문에 $\vert S\vert \leq \vert N_{G’}(S)\vert$가 성립합니다. 따라서 귀납 가정에 의해 $G’$에서 매칭을 마저 완성할 수 있습니다.
2) 공집합이 아닌 어떤 진부분집합 $S \subset X$에 대해, $\vert S\vert = \vert N_G(S)\vert$가 성립하는 경우
귀납 가정에 의해 $S$과 $N_G(S)$은 일대일 매칭이 가능하므로, 매칭 후에 두 집합의 원소들을 $X$와 $Y$에서 제거한 그래프를 $G’(X’, Y’, E’)$이라고 합시다. 이제 $G’$에서 매칭을 마저 완성하기 위해 $G’$이 홀의 조건을 만족함을 보이면 됩니다. 귀류법을 통해 증명하겠습니다.
$G’$이 홀의 조건을 만족하지 않는다고 가정합시다. 즉, $\vert T\vert > \vert N_{G’}(T)\vert$를 만족하는 집합 $T \subseteq X’$가 존재한다고 합시다. 그러면 $N_G(S\cup T)$는 서로 겹치지 않는 두 집합 $N_G(S)$와 $N_{G’}(T)$로 분할할 수 있는데, 전자의 크기는 $\vert S\vert$와 같고 후자의 크기는 $\vert T\vert$보다 작으므로 $N_G(S\cup T)$의 크기는 $\vert S\cup T\vert$보다 작습니다. 이는 $G$가 홀의 조건을 만족한다는 가정에 위배됩니다. 따라서 $G’$은 홀의 조건을 만족합니다.
따라서 두 경우 모두 $G$에서 $X$-완벽 매칭을 찾을 수 있습니다. $\square$
라틴 직사각형의 확장 가능성
이제 Lemma 1을 증명할 준비가 되었습니다.
Lemma 1. $k$-정규 이분 그래프는 항상 완벽 매칭을 갖는다.
이분 그래프 $G(X, Y, E)$가 $k$-정규 그래프라고 합시다. 임의의 부분 집합 $S\subseteq X$에 대해, $S$에 연결된 간선의 집합을 $E_S$라고 하면 $E_S$의 크기는 정점 개수 $\vert S \vert$에 정점의 차수 $k$를 곱한 것과 같습니다. 한편, $S$에 연결된 간선은 $N_G(S)$에도 연결되어 있으므로 $E_S \subseteq E_{N_G(S)}$를 만족합니다. 따라서,
\[E_S = k\vert S\vert \leq k\vert N_G(S)\vert = E_{N_G(S)}\]이므로 부등식의 양 변을 $k$로 나누면 $\vert S\vert \leq \vert N_G(S)\vert$가 성립합니다! 홀의 정리를 적용하면 모든 $k$-정규 이분 그래프는 완벽 매칭을 갖는다는 결론을 얻을 수 있습니다. $\square$
다시 라틴 직사각형 이야기로 돌아와서 이야기를 마무리해 봅시다. $r\times n$ 라틴 직사각형에 행 하나를 추가하는 문제는 $(n-r)$-정규 이분 그래프에서 완벽 매칭을 찾는 문제와 동치이므로, 어떤 $r\times n$ 라틴 직사각형이 주어지든 항상 $(r+1)\times n$ 라틴 직사각형으로, 더 나아가서 $n\times n$ 라진 방진으로 확장할 수 있게 됩니다.
행을 확장할 때에는 최대 이분 매칭 알고리즘을 이용하면 항상 완벽 이분 매칭을 찾을 수 있으므로, 포드-풀커슨 알고리즘 (Ford-Fulkerson Algorithm)이나 호프크로프트-카프 알고리즘 (Hopcroft–Karp Algorithm) 등 최대 이분 매칭을 구하는 알고리즘을 반복하면 $n\times n$ 라틴 방진을 복구하는 것이 가능합니다.
한 행씩 확장하는 것보다 빠른 방법들도 있지만, 이 글의 범위에서 벗어나므로 다루지는 않겠습니다. 관심 있는 독자들은 이분 그래프의 최소 간선 색칠 문제 (Minimum Edge Coloring)에 대해 찾아 보시기 바랍니다. (관련 글: 그래프의 간선 색칠 문제)
연습 문제
- Superdoku (ACM-ICPC North America Qualifier 2018 L번): 글에서 설명한 내용과 동일한 문제입니다.
- $n\times n$ 행렬에 $1$부터 $k$까지의 수를 각각 $n$개씩 채워 넣은 부분 라틴 방진을 생각합시다. $(1 ≤ k ≤ n)$ 이러한 부분 라틴 방진을 반-라틴 방진 (Semi-Latin Sqaure)이라고 부릅니다. 반-라틴 방진의 빈 칸을 채워서 항상 라틴 방진을 만들 수 있음을 보이세요.
- Incidium (Google Code Jam 2020 예선 5번): 라틴 방진을 주제로 한 문제입니다. Lemma 1의 증명 과정과 비슷하게 홀의 정리를 적용해야 하는 문제입니다.
- 링월드 (GCPC 2013 G번 Ringworld): 홀의 정리 응용 문제입니다. 삼성 소프트웨어 멤버십 블로그에도 풀이 글이 있습니다.