Tweakable block ciphers
1. Introduction
안녕하세요, 이번 글에서는 Moses Liskov, Ronald L. Rivest and David Wagner가 작성한 Tweakable Block Ciphers(링크) 논문을 주제로 정했습니다. 참고로 저자중 2번째에 위치한 Ronald L. Rivest는 RSA의 R입니다. 이 논문에서 최초로 Tweakable Block Ciphers라는 개념을 제안했고 이후 Tweak이라는 개념은 대칭키 분야에서 중요하게 쓰이고 있고 최근까지도 관련된 논문이 계속 제시되고 있습니다. 진정한 대가들은 학문에서 새로운 방향성을 제시한다고 하는데 이 논문이 딱 그런 상황에 걸맞는 논문이 맞지 않나 하는 생각이 듭니다.
이번 글을 통해 Tweakable block cipher가 무엇인지 알아보고 이 논문 혹은 그 이후에 제시된 여러 관련 응용들을 같이 알아봅시다.
2. Tweakable block cipher
대칭키 암호학에서는 블록 암호를 빼놓고 얘기할 수가 없습니다. 블록 암호는 고정된 길이의 키 $K$와 평문 $M$을 입력받아 암호문 $C$를 출력하는 암호로, 이를
\[E : \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\]으로 표현할 수 있습니다. 여기서 ${0,1}^k$는 키에, ${0,1}^n$은 각각 평문과 암호문에 대응됩니다.
보통 블록 암호는 키가 고정되어 있을 때 $E_k$가 random permutation일 것으로 간주하고 사용합니다(random function이 아니고 random permutation이어야 inverse, 즉 복호화가 가능합니다). 그리고 이 블록 암호는 deterministic해서 동일한 평문을 넣을 경우 동일한 암호문을 얻게 됩니다. 그렇기 때문에 이 구조는 replay attack 등에 취약하다고 할 수 있습니다. 그렇기 때문에 논문에서는 동일한 평문을 넣더라도 매번 다른 암호문을 얻을 수 있는 새로운 구조 Tweakable block cipher를 제안합니다. Tweakable block cipher는 아래와 같이 나타낼 수 있습니다.
\[\tilde{E} : \{0,1\}^k \times \{0,1\}^t \times \{0,1\}^n\rightarrow \{0,1\}^n\]블록 암호 $E$와 달리 Tweakable block cipher $\tilde{E}$는 정의역에 키와 평문 뿐만 아니라 길이 $t$의 값 $T \in {0,1}^t$를 추가로 넘겨받습니다. 이 추가적인 값 $T$가 바로 tweak입니다.
이 Tweakable block cipher를 만들어내는 디자인은 아주 다양합니다. 이 중에서 가능하면 효율적이게, 구체적으로 말해 키를 교체하는 것 보다 트윅을 교체하는게 더 효율적이게 하는 것이 목표입니다. 또한 tweak은 공개된 값이고 공격자가 임의로 선택할 수 있는 값으로 간주합니다. 그렇기 때문에 Tweakable bock cipher는 설령 공격자가 트윅을 임의로 선택할 수 있어도 안전해야 합니다.
이 논문에서는 tweakable block cipher에 대한 개념들을 정리하고 tweakable block cipher의 구조를 제안하며 그 안전성을 증명합니다.
A. 잘못된 Tweakable block cipher 예시
먼저 Tweakable block cipher의 잘못된 예시로 아래와 같은 구조를 생각해봅시다. $E$는 블록 암호, $K$는 키, $T$는 트윅, $M$은 평문을 의미합니다.
\[\tilde{E}_K(T, M) = E_{K \oplus T}(M)\]이것이 왜 안전하지 않은가를 설명하려면 먼저 Tweakable block cipher가 안전하다는게 어떤 의미인지를 알 수 있어야 합니다. 이전 글에서 특정 구조가 안전함을 보일 때 우리는 그 구조와 random permutation 혹은 random function이 구분될 수 있는지를 고려합니다. Tweakable block cipher 또한 비슷한 맥락에서 Tweakable random permutation과 굉장히 낮은 확률로 구분이 가능하다면 Tweakable block cipher를 안전하다고 말할 수 있습니다. 이 때 Tweakable random permutation은 고정된 tweak $T$와 키 $K$에 대해 random permutation을 만드는 구조입니다.
그러면 위에서 제시한 Tweakable block cipher가 왜 안전하지 않는지를 생각할 때, 우리는 고정된 키에 대해 $E_k$가 random permutation일 경우 $E$를 안전하다고 간주합니다. 하지만 이 정의에서 서로 다른 키를 사용할 때에 대한 상황은 고려가 되지 않고 있고, 극단적으로 모든 키에 대해 $E_K$가 동일하다고 해도 $E$의 안전성에 영향을 주지 않습니다. 그러나 이러한 상황이라면 공격자는 $T$와 상관없이 $M$에 대한 $\tilde{E}_K(T, M)$가 항상 동일함을 통해 tweakable block cipher와 tweakable random permutation을 구분할 수 있습니다.
B. Tweakable block cipher 예시 및 안전성 증명 1
논문에서는 $\tilde{E}_K(T, M) = E_K(T \oplus E_K(M))$을 제안하고 $E$의 안전성과 비교할 때 이 구조가 공격자에게 $\Theta(q^2/2^n)$ 만큼의 어드밴티지를 준다는 사실을 증명합니다. 식으로 표현하면 아래와 같습니다.
\[\mathrm{Sec}_{\tilde{E}}(q,t) < \mathrm{Sec}_{E}(q,t) + \Theta(q^2/2^n)\]이 어드밴티지에 대한 증명은 5단계에 걸쳐 hopping을 하는 방식으로 진행됩니다. 설명을 꼼꼼하게 하는 대신 증명의 흐름을 대략적으로 짚고 넘어가겠습니다.
먼저 공격자가 Tweakable block cipher $\tilde{E}$와 Tweakable random permutation $\tilde{\Pi}$를 구분할 수 있는 능력이 있다고 해보겠습니다.
Case 1. 공격자가 $\tilde{E}K$와 $H^1(T,M) = \Pi(T \oplus \Pi(M))$을 구분할 수 있습니다. 이 경우, 우리는 $E$와 $\Pi$를 구분할 수 있기 때문에(NP 문제에서의 reduction을 생각하면 니니다) Advantage는 $\textrm{Sec}{E}(q,t)$ 이하입니다.
Case 2. 공격자 A가 $H^1$과 $H^2(T,M) = R(T \oplus R(M))$을 구분할 수 있습니다. 이 때 $R$은 random function입니다. 이는 random function과 random permutation의 구분이니 advantage는 $\Theta(q^2/2^n)$입니다.
Case 3. 공격자 A가 $H^2$와 $H^3(T,M) = R_2(T \oplus R_1(M))$을 구분할 수 있습니다. $T \oplus R(M_i) = M_j$ 충돌이 발생하지 않는 한 둘은 구분될 수 없기 때문에 advantage는 $\Theta(q^2/2^n)$입니다.
Case 4. 공격자 A가 $H^3$과 $H^4(T, M) = R(T, M)$을 구분할 수 있습니다. $T_i \oplus R_1(M_i) = T_j \oplus R_1(M_j)$이 발생하지 않는 한 둘은 구분될 수 없기 때문에 advantage는 $\Theta(q^2/2^n)$입니다.
Case 5. 공격자 A가 $H^4$와 $\tilde{\Pi}$를 구분할 수 있습니다. $T$가 고정되어 있을 때 $H^4$와 $\tilde{\Pi}$의 차이는 random function인지 random permutation인지의 차이이기 때문에 Advantage는 $\Theta(q^2/2^n)$ 이하입니다.
Case 1-5를 종합하면 $\textrm{Sec}{\tilde{E}}(q,t) < \textrm{Sec}{E}(q,t) + \Theta(q^2/2^n)$임을 알 수 있습니다.
C. Tweakable block cipher 예시 및 안전성 증명 2
한편 위에서 살펴본 구조는 두 번의 암호화를 필요로 하는데, 논문에서는 해시 함수를 이용하는 대신 한 번의 암호화를 필요로 하고 또 트윅의 길이가 블록의 크기 $n$과 무관해도 되는 또 다른 구조 $\tilde{E}_{K, h}(T, M) = E_K(T \oplus h(T)) \oplus h(T)$를 제안했습니다. 이 구조는 해시 함수의 안전성을 $\epsilon$이라고 할 때 $3\epsilon q^2$만큼의 어드밴티지를 줍니다. 여기서 말하는 해시 함수는 역상 저항성(pre-image resistance), 충돌 저항성(collision resistance) 등이 있는 암호학적 해시 함수는 아니고 조금 다른 특성을 가진 해시함수입니다. 구체적으로 이 해시함수는 $\epsilon$-almost 2-xor-universal($\epsilon-AXU_2$) 해시 함수입니다. $\epsilon$-almost 2-xor-universal 해시 함수의 정의는 아래와 같습니다.
\[\textrm{Pr}_h[h(x) \oplus h(y) = z] \leq \epsilon \textrm{ for all } x, y ,z\]2-xor-universal 해시함수를 이용한 tweakable block cipher의 어드밴티지가 $3\epsilon q^2$임을 증명하기 위해서는 $M_i \oplus h(T_i)$ 혹은 $C_i \oplus h(T_i)$에서 충돌이 나는 경우를 Bad event로 정의한 뒤 H-coefficient Technique을 사용하면 됩니다. 디테일은 생략하겠습니다. 과정을 확인하고 싶으면 논문의 Appendix A를 확인하시면 됩니다.
3. Tweakable Modes of Operation
Tweakable block cipher에 대해 소개할 때 블록 암호는 deterministic해서 동일한 평문을 넣을 경우 동일한 암호문을 얻게 된다, 그렇기 때문에 이 구조는 replay attack 등에 취약하다는 설명을 했었습니다. 암호학에 대해 어느 정도의 지식이 있으신 분이라면 Tweakable block cipher에 대해 모르더라도 대칭키 구조에서 replay attack을 막기 위해 고안된 것을 떠올릴 수 있습니다. 바로 CBC, GCM과 같은 운용 모드(Modes of Operation)입니다. 이러한 운용 모드에서는 블럭의 크기와 동일한 IV(Initial Vector)가 추가로 주어지고 같은 메시지와 키라고 해도 IV가 달라짐에 따라 암호문의 값이 달라집니다. CBC 모드를 이 논문에서 사용하는 표현에 맞게 서술해보면 TBC(Tweak Block Chaining)을 생각할 수 있습니다.
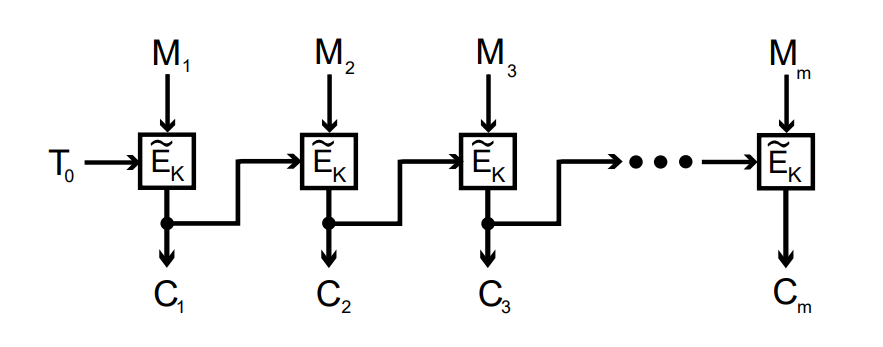
처음 평문에 대한 트윅 $T_0$는 정해져 있고, 그 다음부터는 이전 블럭에서의 암호문이 트윅으로 들어갑니다. CBC 모드에서는 블록 암호의 평문에 이전 블럭에서의 암호문 혹은 IV가 XOR되는 방식이었지만 TBC 모드에서는 XOR되는 대신 트윅으로 정해집니다.
이외에도 블록 암호를 이용해 해시함수를 만드는 구조인 Davies-Meyer hash function의 구조를 이용한 TCH(Tweak Chain Hash), 인증과 암호화를 동시에 제공하는 TAE(Tweakable Authenticated Encryption) 모드 등이 논문에서 같이 제안되어 있습니다.
4. Tweak Length Extension
마지막으로 Kazuhiko Minematsu and Tetsu Iwata가 작성한 Tweak-Length Extension for Tweakable Blockciphers(링크)에 담겨있는 내용을 간단하게 소개해드리겠습니다.
우리에게 원래 $m$비트의 트윅을 받는 어떤 tweakable permutation $\tilde{P}$가 주어져있다고 해봅시다. 그런데 우리는 여기서 트윅의 길이를 $m$비트보다 더 늘리고 싶을 수 있습니다. 이 때 논문에서는 트윅을 늘리면서 안전성을 확보할 수 있는 구조 XTX를 제안하고 있습니다. 트윅을 임의의 길이 $t$비트로 늘이고 싶다고 할 때 XTX 구조는 $O(2^{(n+m)/2})$만큼의 안전성을 제공해줍니다. XTX 구조에서는 $\epsilon$-almost 2-xor-universal($\epsilon-AXU_2$) 해시함수와 함께 $\epsilon$-almost universal($\epsilon-AU$) 해시함수가 추가로 쓰입니다. $\epsilon$-almost universal의 정의는 아래와 같습니다.
\[\textrm{Pr}_h[h(x) = h(y)] \leq \epsilon \textrm{ for all } x, y\]이 때 $\epsilon$-almost 2-xor-universal 해시함수 $H : \mathcal{K} \times \mathcal{T} \rightarrow {0,1}^n$과 $\epsilon$-almost universal 해시함수 $H’ : \mathcal{K}’ \times \mathcal{T} \rightarrow {0,1}^t$에 대해 XTX는 아래와 같이 정의됩니다. 이 때 $\mathcal{K} \times \mathcal{K’}$은 key space입니다.
\[XTX : (K, K', T, X) \rightarrow \tilde{P}(H'_{K'}(T), X \oplus H_K(T)) \oplus H_K(T)\]XTX의 안전성 또한 H-coefficients technique으로 증명이 가능합니다. Bad event는 $\tilde{P}$의 인자 2개가 전부 충돌하거나 $\tilde{P}^{-1}$의 인자 2개가 충돌하는 상황으로 정의하면 됩니다.
5. Conclusion
이번 글에서는 Tweakable Block Ciphers에 대해 설명하고 여러 notion들을 정리해보았습니다. 안전성 증명에 익숙하지 않다면 글이 많이 어려울 것으로 예상되지만 증명의 많은 부분은 건너뛰고 tweak이라는 개념이 무엇인지만 얻어 가더라도 나쁘지 않다고 생각합니다.