April 19, 2022 00:00

Introduction

$k$-nearest neighbor classification이란, $d$차원 공간 위의 point cloud들 (training set)과 그 class가 주어져 있을 때, 새로운 점의 class를 예측하는 한 가지 방법입니다. 자신과 가장 가까운 $k$개의 점의 label 중 가장 많은 것을 선택하는 방법으로, 고전적인 pattern recognition method 중 하나로 소개되었습니다. 오늘은 이 중 그나마 알고리즘의 시각에서 조명이 가능한 $k = 1$ case, 즉, nearest-neighbor classification에 대해 알아봅시다.

1-NN classification and Voronoi diagram

$d = 2$인 경우, 어떤 점 $p$의 nearest neighbor가 $q$일 필요충분조건은 다른 모든 training set의 점 $r$에 대해 $\lVert p - q \rVert < \lVert p - r \rVert$인 것이겠죠. 위 조건을 만족하는 $p$의 범위는 열린 반평면이고, 모든 $r$에 대해 교집합을 취하면 볼록한 영역 (face)이 됩니다.

face들과 그 경계를 모으면 아래 그림과 같이 전체 평면 $\mathbb{R}^{2}$을 분할하게 됩니다. 일반적으로 이를 Voronoi diagram이라고 하고, 각 face를 정점으로 하고 경계를 간선으로 하는, 즉 voronoi diagram의 dual graph를 일반적으로 delaunay triangulation이라고 합니다.

사실상 $1$-NN classification이란 일반적인 점이 voronoi diagram에서 자리하는 face를 찾는 것과 동치이기 때문에, Voronoi diagram을 유지할 수 있으면 됩니다. Voronoi diagram을 만드는 시간 복잡도는 $O(n \log n)$, 공간 복잡도는 평면그래프의 성질에 따라 $O(n)$이기 때문에 유지하는 데 무리가 없습니다.

Voronoi diagram is suboptimal

하지만 의외로 Voronoi diagram은 naive scan보다 좋은 점이 없습니다. Naive scan의 경우 $O(dn)$의 시간복잡도와 $O(1)$의 추가 메모리를 가지는 데 반해, $d$차원 Voronoi diagram의 꼭짓점 개수는 최악의 경우 $\Theta(n^{\lceil d / 2 \rceil})$개에 달하는데다, 어떤 점이 자리하는 Voronoi diagram의 face를 찾는 문제가 간단히 풀리지 않기 때문입니다.

이 상황에서 선택할 수 있는 방법은 크게 두 가지가 있습니다.

• Exact NN 대신, Approximate NN을 계산하자. $1 + \varepsilon$배 정도의 근사해를 $T(n, \varepsilon)$ 시간에 구할 수 있는 방법을 찾자.
• Exact NN을 유지하되, “class-wide Voronoi diagram을 바꾸지 않는” redundant한 점들을 제거하자.

Approximate NN의 경우, Locality-sensitive hashing (LSH)을 이용한 기법이 많이 연구되었습니다. 다음 조건을 만족하는 hash function $h$를 $(r _ {1}, r _ {2}, p _ {1}, p _ {2})$-LSH라고 부릅니다.

• $\lVert p - q \rVert \le r _ {1}$일 때, $\Pr[h(p) = h(q)] \ge p _ {1}$
• $\lVert p - q \rVert \ge r _ {2}$일 때, $\Pr[h(p) = h(q)] \le p _ {2}$

즉, 두 점이 가까울 때 hash collision이 발생할 확률이 높은 hash function을 말합니다. $\rho = \frac{-\log p _ {1}}{-\log p _ {2}}$라고 두면, $(1, c, p _ {1}, p _ {2})$-LSH가 주어졌을 때 다음 정리가 성립합니다. (Indyk 1998)

Theorem. (Indyk 1998) Hash function을 계산하는 데 걸리는 시간이 $\tau$라고 하면, $c$-approximate Nearest Neighbor query를 $O((d + \tau)n^{\rho} \log _ {1 / p _ 2} n)$ 시간복잡도와 $O(dn + n^{1 + \rho})$ 시간복잡도로 해결할 수 있다.

Theorem. (Andoni \& Indyk 2012) Euclidean space에 대해, $\rho = \frac{1}{c^2} + o(1)$인 LSH $h$가 존재한다.

하지만 차원이 높아질수록 $c$도 더 작아져야 하는 암묵적인 경향성이 있기에, approximate NN에는 기본적인 한계가 존재합니다.

점 개수의 두 번째 방법은 일반적으로 class의 수가 점의 수보다는 훨씬 작아야만 효율적일 것입니다. 물론 이런 식으로 여러 “상식적인 가정”들을 추가해서 좋은 결과를 얻어내는 것도 좋지만, 오늘의 메인 논문인 Eppstein (2022) 가 제시한 조건은 훨씬 유연합니다.

• 모든 점들은 General position일 필요도 없고, class 수도 제한이 없음.
• redundant한 점들을 제거하고 남은 “relevant”한 점들의 개수를 $k$로 둠. 여기서 $O(k)$ 짜리 naive scan으로 nn을 찾거나, 다른 알고리즘을 사용할지는 자유롭게 결정할 수 있음
• Relevant한 점을 output-sensitive complexity $O(f(n, k, d))$에 빠르게 찾을 수 있음
• “Natural”한 dataset에서, $k = O(n^{(d - 1) / d})$ 정도일 것으로 기대할 수 있음.

알고리즘은 간단하지만, 계산기하학의 주요한 성과인 euclidean MST, high-dimensional convex hull 등을 블랙박스로 사용합니다. 이는 곧 블랙박스로 사용된 알고리즘의 시간복잡도에 따라 이 알고리즘 또한 시간복잡도가 줄어들 것을 시사합니다.

Preliminaries

Voronoi complex and Delaunay graph

Training set $T \subseteq \mathbb{R}^{d}$라고 둡시다.

앞서 정의한 것과 비슷하게, $d$차원에서 training set $p \in T$에 대한 Voronoi cell $V _ {p}$를 $V _ {p} := { x : \forall q \in T \; \lVert p - x \rVert \le \lVert q - x \rVert }$로 정의하면, $V _ {p}$는 convex polyhedron을 이룹니다. $T$가 유한집합이기 때문에, 모든 $V _ {p}$는 적당한 $d$차원 구를 포함하는 $d$차원 집합입니다.

$V _ {p}$들의 interior point들은 서로 겹치지 않고, boundary는 겹칠 수 있습니다. cell들의 유한 intersection으로 나타낼 수 있는 집합을 face라고 두고, $d-1$차원짜리 face를 wall, $d-2$차원짜리 face를 junction 이라고 두겠습니다. 익숙한 2차원 그림의 경우 wall은 변(side), junction은 꼭짓점에 대응됩니다. $d > 2$일 때도 junction $j$에 수직한 평면으로 voronoi diagram을 잘라서 그 단면을 보면 $j$를 포함하는 wall은 반직선으로, 그리고 $j$를 포함하는 cell은 cone으로 표현됩니다.

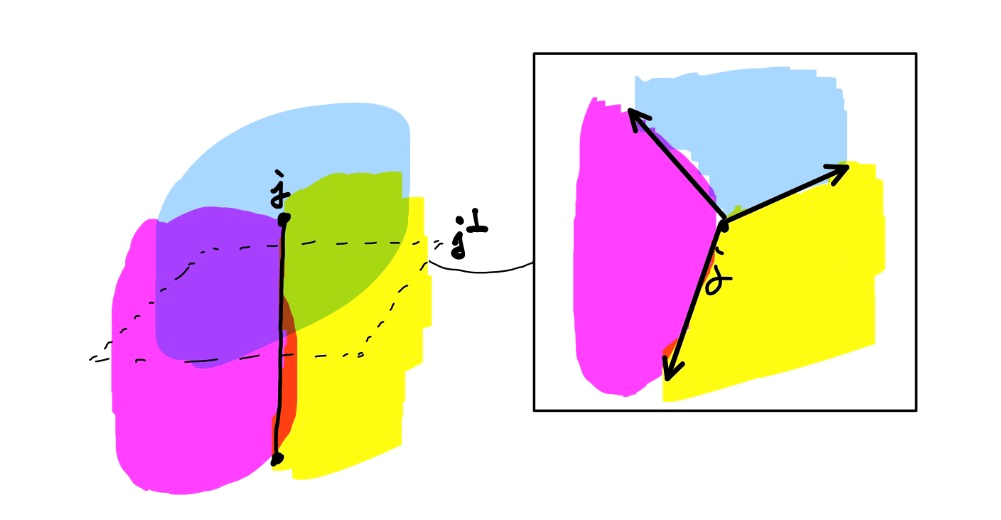
만약 모든 점이 general position에 있다면 - 임의의 $d + 2$개의 점이 같은 sphere 위에 존재하지 않다면 - 모든 단면에는 3개의 반직선과 3개의 cone이 존재합니다. 아래는 2차원에서 non general position에 있는 voronoi diagram을 나타냅니다.

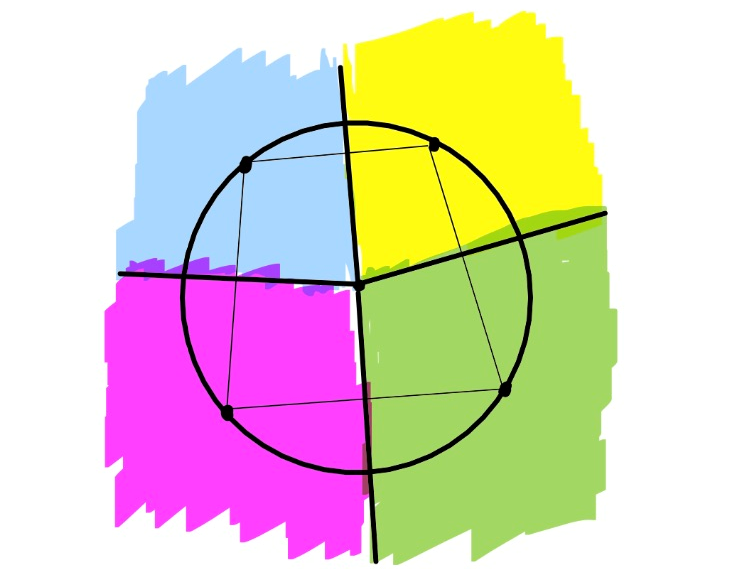
$2$차원에서 dual graph로 정의되던 delaunay graph도 비슷하게 정의할 수 있습니다. 각 cell을 정점으로 하고, 두 cell의 교집합이 wall일 때 간선을 이어준 것을 delaunay graph라고 부릅니다. 만약 모든 점이 general position에 있다면 delaunay graph는 chordal graph가 되고 이를 delaunay triangulation이라고도 부릅니다. 물론 소개할 알고리즘은 non-general position 세팅에서도 잘 작동합니다.

Black-box 1 : Euclidean MST

Eppstein의 알고리즘에 첫 번째로 들어가는 재료인 Euclidean MST입니다. Prim algorithm을 사용하면 $O(n^{2})$ 시간에 구해줄 수 있습니다. 만약 $2$차원 데이터라면 $O(n \log n)$ 시간에 delaunay trinagulation을 구한 뒤 MST를 구하는 방법이 가능했겠지만, $d > 2$에서는 불가능한 방법입니다. Agarwal (1991), Matousek (1995) 등에 의해서 밝혀진 deterministic solution이 현재로서는 최선의 방법으로 여겨집니다. 해당 방법의 시간 복잡도는 $O(n^{2 - \frac{2}{\lceil d / 2 \rceil + 1} + \varepsilon})$ for all $\varepsilon > 0$입니다. 구체적으로 $d = 3$이라면 randomized $O((n\log n)^{4/3})$에 동작합니다.

$d$가 상수가 아닐 때, 가령 $d = (\log n)^{\Omega(1)}$ 정도라고 가정합시다. 이 경우, 유명한 추측인 strong exponential time hypothesis가 참이라면 Closest pair가 $O(n^{2 - \varepsilon})$ 시간에 풀릴 수 없다는 것을 증명할 수 있습니다. Closest pair가 Euclidean MST보다는 간단하기 때문에 EMST 또한 $d$가 unbounded일 때는 subquadratic solution을 찾지 못하고 있습니다.

일반적인 dimension에서도 다음의 Lemma가 성립합니다.

Lemma. EMST는 Delaunay graph의 subgraph이다.

Proof. EMST의 간선 $pq$에 대해 그 중점을 $r$이라고 하자. 만약 $\lVert p - r \rVert > \lVert p - s \rVert$인 정점 $s$가 존재한다면 $\lVert p - s \rVert, \lVert q - s \rVert < \lVert p - q \rVert$가 성립한다. $ps, qs$ 중 하나는 EMST에 포함되어 있지 않으므로 $pq$를 빼고 둘 중 빠진 것을 추가하면 Minimum Spanning Tree 조건에 모순. 따라서 $r$은 $V _ {p}$와 $V _ {q}$의 경계에만 존재한다. 또한 $pq$와 수직하고 $r$을 중심으로 하는, 충분히 작은 $d-1$차원 ball이 존재하여 이 안에 존재하는 점들은 모두 같은 성질을 만족하게 할 수 있고, 결국 $V _ {p}, V _ {q}$의 교집합은 wall임을 증명할 수 있다. $\square$

$d = 2$인 경우에 Delaunay graph가 planar이므로, EMST를 $O(n\log n)$ 시간에 찾는 데 저 lemma가 강력하게 작용했습니다. $d > 2$에서는 delaunay graph가 완전그래프가 될 수 있기 때문에 시간복잡도 차원에서는 별 의미가 없으나, 추후 설계할 알고리즘 정당성 증명에 큰 역할을 합니다.

Black-box 2 : Convex hull on general dimension

$d > 2$ 차원에서 convex hull이 힘든 이유는 CCW 연산이 잘 정의되지 않기 때문입니다. 대신 점 $p$ convex hull에 들어갈 수 있는지는 모든 $q \neq p$에 대해 $v \cdot p > v \cdot q$ 를 만족하는 $v$가 존재하는지를 묻는 LP 문제로 환원할 수 있습니다. $d$가 고정되어 있다면 조건식이 $A$개인 LP는 $O(A)$ 시간에 해결할 수 있습니다.

단순히 모든 점 $p$에 대해 LP를 해결하는 방식으로 $O(n^2)$에 convex hull을 구할 수 있지만, 간단하게 $O(nk)$ 시간복잡도를 만들 수 있습니다. 이와 같이 output-sensitive한 결과를 만드는 것은 $k$가 “랜덤한 상황”에 대해서 충분히 작을 것이라는 기대가 있기 때문입니다. python 유사 코드는 아래와 같습니다.

import numpy as np
extreme _ points = [] # make an empty set

def is _ extreme(S, p): # determine if p is extreme in the set S 
    pass # SOLVE LP and return v (feasible sol) or None (if infeasible)

for p in input _ points:
    v = is _ extreme(extreme _ points + [p], p)
    if v is None:
        continue
    else: # enters here at most k times
        p _ opt = p
        for q in input _ points:
            if np.dot(q, v) > np.dot(p _ opt, v):
                p _ opt = q
        extreme _ points.append(p _ opt)

$O(k)$ 시간이 걸리는 LP를 최대 $n$번, $O(n)$ 시간이 걸리는 else 절을 최대 $k$번 들어가기 때문에 전체 시간복잡도가 $O(nk)$로 유지됩니다.

여기까지가 simple algorithm으로 줄일 수 있는 영역이고, dimension이 높아지기 시작하면 힘들어집니다. $d$차원에서 크기가 $n$인 점집합의 convex hull이 $\Theta(n^{\lfloor d / 2 \rfloor})$까지 커질 수 있기 때문인데요, 3차원까지는 $O(n \log n)$ 이 걸리는 간단한 알고리즘이 있지만 일반적인 차원에서는 같은 방법으로 접근해서는 $O(n \log n + n^{\lfloor d / 2 \rfloor})$가 붙게 됩니다. Timothy Chan (1996)의 결과에 따르면 output-sensitive한 결과는 아래와 같습니다.

$O(n \cdot (\log k)^{O(1)} + (nk)^{1 - \frac{1}{1 + \lfloor d / 2 \rfloor}}(\log n)^{O(1)})$

Polarity

어떤 원점 $O$를 기준으로 하는 unit sphere가 주어져 있을 때, 점 $x$의 inversion $\overline{x}$는 $\frac{x}{\lvert x \rvert^{2}}$으로 정의합니다. 이 때 Polarity operation은 점과 점이 아닌 점과 hyperplane을 대응시키는 방법입니다.

• 점 $p$가 주어져 있으면, $\overline{p}$를 지나고 $Op$에 수직한 hyperplane $H$가 $p$의 polarity transformation입니다.
• hyperplane $H$가 주어져 있을 때, $O$에서 $H$에 내린 수선의 발 $n \in H$를 구하면 $\overline{n}$이 $H$의 polarity transformation입니다.

둘은 정확히 역과정에 대응되며, 이 변환을 $H = \varphi(p)$라고 나타낼 때 $q \in \varphi(p) \iff p \cdot q = 1$입니다. 또한 $p \cdot q - 1$의 부호에 따라 $H$의 어느 쪽에 있는지 (sidedness)가 결정됩니다.

이후 제안할 알고리즘에 유용하게 사용될 lemma를 소개합니다.

Lemma. (Extremity-Adjacency duality) 원점 $O$를 포함하지 않는 집합 $P = {p _ {1}, \cdots, p _ {n}}$이 주어져 있을 때, $\overline{P} = {\overline{p _ 1}, \cdots, \overline{p _ {n}}}$를 생각하자. 이 때 $\overline{p _ {i}}$가 $\overline{P} + O$의 convex hull에 속하는 것과, $P + O$의 Voronoi diagram에서 $p _ {i}$와 $O$ 사이에 wall이 존재하는 것은 동치이다.

Proof. 일반성을 잃지 않고, $O$를 기준으로 $\overline{P}$를 잘 scaling하여 (제 계산으로는 2배로) $\varphi(\overline{p _ {i}})$가 곧 $p _ {i}, O$의 수직이등분-hyperplane $W _ {i}$ (곧, ${p _ {i}, O}$ 2개로만 만든 voronoi diagram의 유일한 wall) 이 되도록 할 수 있습니다. 이 작업은 convex hull을 바꾸지 않기 때문입니다.

$\overline{p _ i}$가 $\overline{P} + O$의 convex hull 위에 존재한다면, $\overline{p _ i}$를 포함하는 반평면 $H _ {i}$가 존재하여 모든 $\overline{p _ j} \neq \overline{p _ i}$가 $H _ {i}$를 기준으로 한 쪽에 있도록 할 수 있습니다. 이 때 $h = \varphi^{-1}(H _ {i})$로 두면, $h$는 모든 $W _ {j} \neq W _ {i}$에 대해 한 쪽에 속해 있음을 알 수 있습니다. 정확히는 $\lVert h - O \rVert = \lVert h - p _ {i} \rVert < \lVert h - p _ {j} \rVert$가 모든 $j \neq i$에 대해 성립하는 것으로, 이는 곧 Voronoi wall의 존재성을 입증합니다. 반대 방향도 위 성질을 거꾸로 써서 증명할 수 있습니다. $\square$

또 하나의 Lemma를 증명 없이 소개합니다.

Lemma. (Existence of Sides) Delaunay graph에서 같은 class로만 묶인 한 connected component를 $C$라 하고, $C$를 둘러싸는 경계의 wall들을 $\partial C$라고 하자. 이 때 $\partial C$의 wall들 중 junction으로 이어진 각 component $K$에 대해, $K$를 경계로 갖는 set of voronoi cells가 존재하며, 이러한 $K$를 “decision boundary component (DBC)”, 이러한 set을 “side”라고 한다.

엄밀히 state하기 위해선 위상수학 용어가 필요하지만, 여기서는 그리드의 voronoi diagram을 이용하는 것으로 대체합니다. Eppstein (2022)의 논문 Figure를 인용합니다.

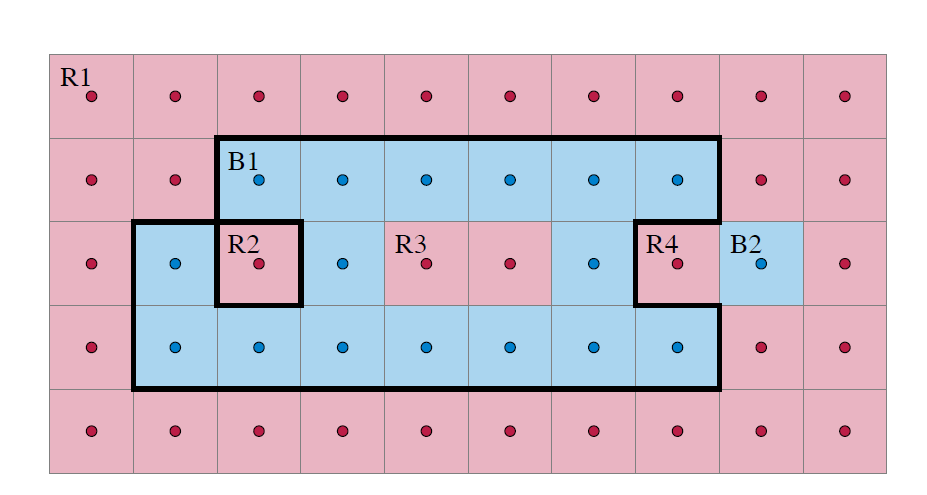
위 그림에서 $\partial(B1)$은 굵은 선으로 표기된 바깥쪽 경계 $K _ {1}$, R3와 맞닿은 안쪽 경계 $K _ {2}$를 연결 컴포넌트로 갖습니다. 이 때 $K _ {1} = \partial(B1 \cup R3)$, $K _ {2} = \partial(R3)$가 성립합니다. 단, $K$의 side가 반드시 한 class로만 이루어져 있을 필요가 없다는 것에 주의하세요.

Eppstein’s algorithm

이 두 가지 blackbox를 가지고 설계한 “relevant point”를 찾는 알고리즘은 아래와 같습니다.

1. Euclidean MST $T$를 구하고, $T$의 간선 $uv$에 대해 $u$의 class와 $v$의 class가 다르면 $u, v$를 relevant point의 집합 $R$에 추가한다.
2. 모든 $r \in R$에 대해 다음을 반복한다.
   1. $r$과 class가 다른 모든 점을 unit sphere에 대해 반전(invert) 시킨 점집합 $I _ {r}$을 만든다.
   2. $I _ {r}$의 convex hull을 구하고, hull의 정점을 다시 unit sphere에 invert한 원본 점들을 $R$에 추가한다.

Relevant point가 $n$개 중 $k$개라고 하면, 알고리즘의 시간복잡도는 $O(EMST + k \cdot (n + HULL))$인 것을 알 수 있습니다.

• Simple algorithm으로 $EMST = O(n^2)$, $HULL = O(nk)$를 선택하면 시간복잡도는 $O(n^{2} + k^{2} n)$이 됩니다. 이는 Clarkson (2015)의 $O(\min(n, k)n^{2} \log n)$을 앞서는 수치입니다.
• 복잡한 알고리즘을 쓰면 시간복잡도는 $\tilde{O}(n^{2 - \frac{2}{1 + \lceil d / 2 \rceil}} + k(nk)^{1 - \frac{1}{1 + \lfloor d / 2 \rfloor}})$으로 나타납니다. 이 때 $d$는 $n$과 무관한 상수여야 합니다.

이 알고리즘의 correctness를 증명하는 것으로 이 글을 마치겠습니다.

Correctness

1. Only “relevant points” are sampled.

Lemma. (EMST endpoints are relevant) training set의 간선 $uv$가 서로 다른 class로 이루어진 두 점을 잇는다고 하자. 이 때 $u, v$는 각각 relevant하다.

Proof. EMST는 Delaunay graph의 subgraph이므로, $u, v$ 사이에 wall이 존재합니다. wall의 relative interior에 속한 점 $w$는 $\lVert w - u \rVert = \lVert w - v \rVert < \lVert w - x \rVert$를 모든 $x \in T - {u, v}$에 대해서 만족합니다. $w$를 $u$쪽 (혹은 $v$쪽)으로 충분히 작게 (부등식의 방향이 바뀌지 않을 정도로) 움직였을 때, $u$ (혹은 $v$)가 존재할 때와 존재하지 않을 때 nearest neighbor가 달라지므로 $u, v$는 relevant합니다.

Lemma. (Eppstein’s algorithm adds only relevant points.) Training set에 대해 relevant한 점 $r$과, $r$과 다른 class의 점 $p$에 대해 $p$가 Eppstein’s algorithm의 convex-hull 조건을 만족한다고 하자. $p$는 training set에 대해 relevant하다.

Proof. Extremity-Adjacency duality에 의해, $p, r$ 사이에는 voronoi wall $W$가 존재합니다. 단, 여기서 voronoi diagram은 ${r}$ + ($r$과 다른 class의 점들) 만 가지고 그려졌다는 것에 주의합시다. $w \in W$를 $W$의 relative interior 안에서 “잘 선택”하여, 선분 $pw$가 전체 training set의 voronoi diagram 중 $d-2$차원 이하의 object와는 만나지 않게 할 수 있습니다.

이제 $r$과 같은 class의 점들만 유의해주면 되는데, 선분 $pw$의 점 $x$를 “가장 가까운 $r$-classed 점 $\rho _ {x}$와 $p$까지의 거리가 같은 점”으로 정의합니다. $\lVert \rho _ {x} - x \rVert$가 연속함수이기 때문에 중간값 정리로 $x$의 존재성을 보일 수 있고, 만약 어떤 $x$에 대해 $\rho _ {x}$가 될 수 있는 점이 둘 이상 있다면 이는 $x$가 세 점 이상의 nearest neighbor를 갖는다는 뜻입니다. 이는 $w$를 우리가 앞에서 잘 골라주었기 때문에 발생할 수 없는 사건이고, 앞서 EMST와 관한 Lemma를 증명할 때 사용한 argument를 사용해주면 됩니다.

2. All relevant points are scanned.

어떤 voronoi wall $w = V _ {p} \cap V _ {q}$에 대해, $p, q$를 $w$의 “defining site”라고 부르도록 합시다.

Step 1. 모든 DBC $K$에 대해, 이 중 적어도 한 wall의 defining site는 relevant point로 detect된다.

Proof. 편의상 $K$의 side를 $E$라고 둡시다. Euclidean MST는 모든 점을 연결하므로, 반드시 $E$ 바깥에서 $E$ 안으로 들어가는 간선 $e$를 포함하게 됩니다. 이 때 DBC의 정의상 $e$는 서로 다른 두 class를 잇는 간선이고, $e$의 두 endpoint $u, v$는 $K$의 voronoi wall을 define합니다. 따라서 Euclidean MST를 이용한 초기화 과정에서 각 DBC의 defining site가 하나 이상 들어가게 됩니다. $\square$

Step 2. (Opposite of DBC) DBC $K$가 주어져 있을 때, Eppstein algorithm이 wall $w \in K$의 한 defining site $p$를 relevant로 detect했다고 하자. 이후 다른 한쪽의 defining site $q$도 relevant가 된다.

Proof. $S _ {p}$를 $p$와 다른 class의 점들 + ${p}$로 정의하자. DBC의 정의상 $q, p$는 전체 training set $T$의 Delaunay graph에서 인접하고, 그 subgraph인 $S _ {p}$의 delaunay graph에서도 그렇다. Extremity-Adjacency duality lemma에 의해 Eppstein’s algorithm이 $q$를 detect한다.

Step 3. (Explore DBC through junctions) Wall $w, w’$이 junction $j$를 공유하고, $w, w’$가 이루는 angle 속의 점들은 전부 같은 class를 갖는다고 하자. DBC에서 인접한 두 wall을 잡는 것이 특수한 사례이다. 이 때, $w$의 defining site가 detect되면 $w’$의 defining site도 detect된다.

Proof. 편의상 $p$를 해당 angle 쪽에 있는 $w$의 defining site, $q$를 angle 바깥에 있는 $w’$의 defining site라고 정의합니다. $j$의 link (자신과 수직한 평면을 잡고 wall을 반직선, site를 wedge로 생각하기) 를 생각하면 $S _ {p}$ 상에서 $q, p$가 결국 인접하게 됨을 알 수 있습니다. 설명은 생략. 따라서 역시 Extremity-Adjacency duality lemma에 의해 증명됩니다. $\square$

Step 4. (All relevants are detected)

Proof. $r$이 relevant point라고 하고, $q$가 그 witness라고 합시다. 즉, $r$과 class가 다른 어떤 second-nearest neighbor $p$가 존재하여 $\lVert r - q \rVert < \lVert r - p \rVert <\mathrm{(etc)}$가 성립한다고 합시다. 그렇다면 $p, q$는 그 중점을 지나는 Voronoi wall $w$를 공유하게 되고, $w$는 $r$의 class를 감싸는 한 DBC $K$에 포함됩니다. Step 1-3에 의해서 $r$은 Eppstein’s algorithm에 의해 detect됩니다. $\square$

사실 우리가 그동안 “너무 당연하게 여기고” 답변을 피했던 질문이 있습니다. 과연 Relevant point만 남겨도 Voronoi diagram이 같게 유지될까요? Irrelevant (redundant) point를 하나 빼도 당장 voronoi diagram이 바뀌지는 않지만, 이로 인해 다른 irrelevant point가 relevant point로 바뀌는 일은 없을까요?

DBC를 생각하면 이에 간단하게 “그런 일은 없습니다.” 라고 답할 수 있습니다. Irrelevant point는 DBC를 만드는 데 어떤 기여도 하지 않고, 제거해도 DBC를 바꾸지 않습니다. 따라서 Relevant point만 남겨서 점집합의 개수를 줄인다는 발상은 타당합니다.

Summary

이 글에서는 Eppstein의 SOSA22 논문, “Finding Relevant Points for Nearest-Neighbor Classification”을 리뷰하면서 Nearest Neighbor framework를 꽤 복잡하게 다루어보았습니다. 일반적인 dimension에서는 convex hull, euclidean mst 등을 구하는 직관적인 방법이 먹히지 않는다는 점과, 일반화된 voronoi diagram을 다루는 과정은 통상적인 Problem-Solving 범위보다는 연구 범위에 더 가깝습니다.

추후 포스팅에서는 이 글에서 black-box로 사용한 알고리즘이나, 다소 생소한 접근처럼 보이는 main algorithm의 motivation에 대해 논해보겠습니다.

References

• Eppstein, David. (2021). Finding Relevant Points for Nearest-Neighbor Classification.

• Chan, T.M. Output-sensitive results on convex hulls, extreme points, and related problems. Discrete Comput Geom 16, 369–387 (1996). https://doi.org/10.1007/BF02712874

• Agarwal, P.K., Edelsbrunner, H., Schwarzkopf, O. et al. Euclidean minimum spanning trees and bichromatic closest pairs. Discrete Comput Geom 6, 407–422 (1991). https://doi.org/10.1007/BF02574698