Large S-box의 암호학적 성질 및 대수적 공격

1. Introduction

대칭키 암호화 시스템은 선형 연산과 비선형 연산을 반복적으로 적용해 키와 암호문 혹은 평문과 암호문의 관계를 가립니다. 이 때 S-box는 비선형 성질을 제공하는 중요한 역할을 합니다.

DES에서는 6비트의 입력을 받아 4비트를 출력하는 S-box가 사용되었고 AES에서는 8비트의 입력을 받아 8비트를 출력하는 S-box가 사용되었습니다. 암호가 안전하기 위해서는 S-box가 편향되지 않고 잘 정의되어야 합니다. 예를 들어 S-box의 차분 성질이나 선형 성질의 편향이 클 경우 이를 이용한 차분 공격 혹은 선형 공격이 가능할 수 있습니다.

직관적으로 생각했을 때 S-box가 크면 클수록 이러한 성질의 편향을 가질 확률이 줄어들 것입니다. 예를 들어 AES의 SubBytes 단계에서 바이트 단위의 작은 S-box를 16개 쓰는 대신 그냥 32비트의 입력을 받아 32비트의 출력을 하는 S-box를 4개 쓰거나 128비트의 입력을 받아 n비트의 출력을 하는 아주 큰 S-box(Large S-box)를 1개 쓴다면 AES가 더 안전할 수 있겠다는 생각을 할 수 있습니다.

만약 안전성만 생각한다면 위에서 언급한 내용이 맞습니다. 하지만 우리는 안전성과 같이 효율성 또한 고려해야 하기 때문에 Large S-box를 활용하는데에 제한이 있습니다. 예를 들어 8비트 S-box는 lookup table을 만들 수 있습니다. 쉽게 말해서 256칸 배열을 하나 정의해 입력에 대한 출력을 바로 알 수 있습니다. 하지만 S-box의 크기가 32비트 혹은 256비트라면 S-box에 대한 lookup table을 만드는게 공간의 한계로 불가능하고 S-box의 출력을 계산하기 위한 별도의 함수를 정의해야 합니다. 그리고 S-box가 좋은 성질을 가지려면 당연히 해당 함수의 연산은 아주 복잡해야 할 것이고 이는 곧 성능의 감소로 이어집니다.

이러한 성능상의 단점에도 불구하고 S-box를 크게 설계할 경우 암호의 안전성을 높일 수 있고 이를 이용해 라운드의 수를 줄일 수 있기 때문에 Large S-box를 이용한 암호가 드물게 제시되곤 합니다. Large S-box를 설계하는 방식은 굉장히 다양하지만 보편적인 방법 중 하나로, $n$비트의 입력이 들어온다고 할 때 입력을 $GF(2^n)$ 필드에 대한 역원으로 생각하는 방법이 있습니다. AES의 경우도 비록 Large S-box는 아니지만 S-box가 $GF(2^8)$에 대한 역원으로 정해져 있습니다.

S-box를 필드에 대한 역원으로 두었을 때 암호학적 공격으로부터 안전한지에 대한 분석은 여러 연구 결과로 제시가 되어 있습니다. 실제 Large S-box를 이용한 암호들을 살펴보고 또 안전성에 대해 논의를 해보겠습니다.

2. Large S-box를 기반으로 한 암호

Rasta

(논문) 맨 처음 소개드릴 암호는 CRYPTO 2018에서 제시된 Rasta 암호입니다. 해당 암호는 Multi party computation 혹은 Fully homomorphic encryption에서 사용할 수 있도록 AND 연산을 최소화한 암호입니다. 왜 MPC나 FHE에서 AND 연산을 최소화하는게 좋은건지는 예전에 작성한 글에서 간략하게 언급을 해두었습니다.

Rasta의 구조는 아래와 같습니다.

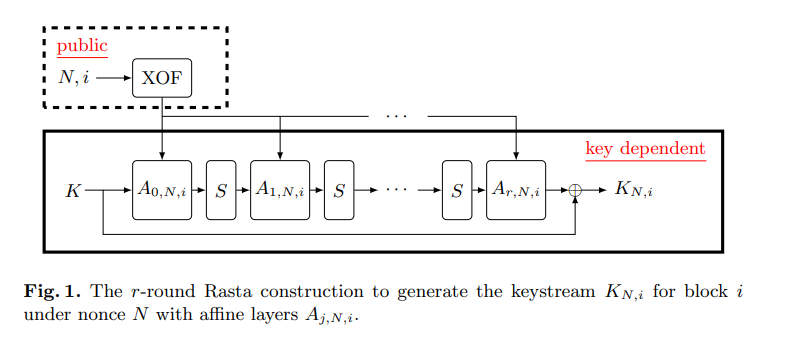
굵은 실선으로 되어있는 부분이 암호화 루틴이고 $A$로 표시된 선형층과 $S$로 표시된 비선형층을 반복해서 지나감을 확인할 수 있습니다. 선형층은 블록의 번호 $i$와 nonce $N$을 가지고 만들어지며, 입력을 $GF(2)$의 길이 $n$ 벡터로 간주하고 미리 정의된 행렬 A와 곱하는 방식입니다.

비선형층은 크기 $n$의 S-box인데 필드에 대한 역원은 아니고 χ-transformation이라는 이름의 $y_l = x_l \oplus x_{l+2} \oplus x_{l+1}x_{l+2}$ 라는 형태($x_i, y_i$는 비트) 비선형 연산을 진행합니다.

총 라운드 수는 안전성 비트에 따라 4 이상으로 정해집니다. AES가 10라운드, DES가 16라운드였던 것과 비교하면 비교적 적은 라운드를 거치더라도 암호가 안전함을 확인할 수 있습니다.

MiMC

(논문) MiMC는 Minimal Multiplicative Complexity의 약어로, 이 암호 또한 MPC 혹은 FHE에서의 쓰임을 고려해 만들었습니다.

MiMC의 구조는 아래와 같습니다.

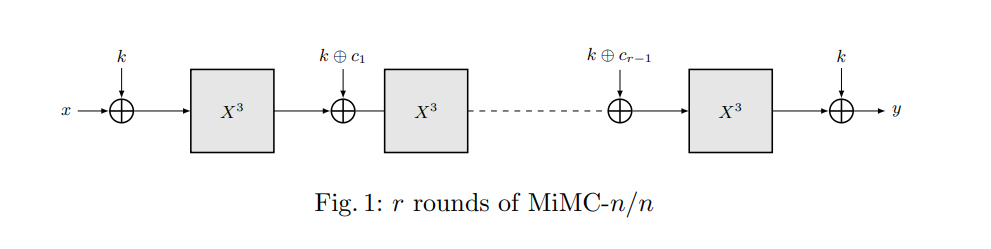
MiMC에서는 $F(X) = x^3$이라는 아주 단순한 형태의 S-box를 사용합니다. 그리고 선형 연산은 LowMC에서와 같이 단순히 키와 라운드 상수 $c_i$를 XOR하는 방식으로 이루어집니다. 이러한 구조적인 특성상 SNARK라는 이름의 영지식 증명을 할 때 효율적임을 논문의 주 contribution으로 내세우고 있습니다. 다만 interpolation attack이라는 이름의 대수적 공격으로부터 안전하기 위해 라운드의 수는 70 이상으로 굉장히 큰 편입니다.

Rain

(논문) Rain은 영지식 증명 기반 전자서명을 효율적으로 만들기 위한 일방향 함수로 제안된 블록 암호입니다. Rain의 구조 또한 굉장히 단순합니다.

S-box는 $GF(2^n)$에 대한 역원이고, 행렬 곱셈($M_i$)과 키 및 라운드 상수의 XOR을 반복 적용합니다. 라운드 수는 기본적으로 3을 추천하나 더 안전하게 하고 싶으면 4를 사용해도 됩니다.

아무리 Large S-box를 사용하는게 암호학적으로 큰 이득을 준다고 해도 3라운드만을 거친다는건 다소 놀라운 일이고 한편으로는 공격이 가능한 것은 아닌가 하는 약간의 의구심을 불러일으키기도 하는데, 일단 논문에서는 차분 및 선형 분석, 그뢰브너 기저 공격, Interpolation attack, Linearlization attack등 다양한 공격에 대한 분석을 진행해 Rain 암호가 안전함을 보이고 있습니다.

3. Large S-box의 안전성

위에서 소개한 여러 예시에서 볼 수 있듯 MiMC를 제외하면 Large S-box를 사용했을 때 대부분의 경우 라운드의 수가 줄어드는 것을 확인할 수 있습니다. 기본적으로 새로운 암호를 설계한 후 라운드 수를 정하는 방법은 비교적 단순합니다. 지금까지 알려진 다양한 공격들을 새로운 암호에 적용해보고, 공격이 불가능할 때 까지 라운드 수를 늘립니다. 이러한 분석을 진행할 때 자연스럽게 Large S-box의 성질에 대한 논의가 필요하게 됩니다.

차분 확률

우선 $GF(2^n)$ 필드의 역원을 생각해봅시다. 이 때 어떤 원소 $a \in GF(2^n)$에 대해 $a^{-1} = a^{2^n-2}$입니다.

입력 차분이 $a$, 출력 차분이 $b$인 차분 확률을 식으로 나타내면 아래와 같습니다.

\[\vert \{x \in GF(2^n) \space \vert \space x^{-1} \oplus (x \oplus a)^{-1} = a\} \vert / 2^n\]

이 차분 확률이 모든 $a, b$ 쌍에 대해 충분히 작을수록 차분 공격으로부터 안전합니다.

만약 $x \not\in {0, a}$일 경우 식을 아래와 같이 정리할 수 있습니다.

\[bx^2 + abx - a = 0\]

이 식은 2차식이니 당연히 최대 2개의 해를 가집니다. 또한 $x$가 0 혹은 $a$일 가능성까지 고려하면 차분 확률은 최대 $4 / 2^n$으로, 가장 이상적인 경우에도 차분 확률은 $2 / 2^n$임을 감안하면 $GF(2^n)$ 필드의 역원은 아주 낮은 차분 확률을 가집니다. 참고로 $n$이 홀수이면 이 수치는 $2 / 2^n$으로 줄어듭니다.

선형 확률

선형 확률은 입력에 대한 마스킹이 $a$, 출력에 대한 마스킹이 $b$라고 할때 아래와 같은 식으로 나타낼 수 있습니다.

\[(\vert \{x \in GF(2^n) \space \vert \space \langle x, a \rangle = \langle x^{-1}, b \rangle \} \vert / 2^n) - 1/2\]

만약 $x^{-1}$이 랜덤하다면 $\langle x, a \rangle = \langle x^{-1}, b \rangle$일 확률은 1/2이기 때문에 이 확률이 얼마나 1/2로부터 편향되었나를 계산하면 그 것이 선형 확률이 됩니다. 이 선형 확률이 모든 $a, b$ 쌍에 대해 충분히 작을수록 선형 공격으로부터 안전합니다.

선형 확률 또한 차분 확률을 계산한 것과 비슷한 방법을 통해 $n$이 짝수일 때 확률이 최대 $2^{n/2}$임을 보일 수 있고, 가장 이상적인 상황에서의 확률이 $2^{(n-1)/2}$이기 때문에 굉장히 낮은 수치임을 알 수 있습니다.

이와 같이 Large S-box를 사용하는 경우 차분 공격과 선형 공격은 사실상 원천봉쇄된다고 생각할 수 있고, Rain에서도 실제로 차분 공격과 선형 공격은 불가능하다고 여겨졌습니다.

4. 대수적 공격

지금까지 암호를 분석할 때에는 차분 공격, 선형 공격과 이들의 여러가지 변형인 부메랑 공격, 불능 차분 공격, 차분-선형 공격 등이 많이 활용되었고 이들은 실제로 1970-90년대에 설계된 여러 암호를 공격하는데에 아주 효과적으로 사용되었습니다. 한편 이번에는 암호를 공격하는 새로운 기법인 대수적 공격들을 소개해드리려고 합니다. 대수적 공격은 특히 이번 글에서 다루고 있는 필드의 역원과 같은 대수적 구조를 사용한 암호에 대해 굉장히 위협적으로 작용할 수 있습니다. 그뢰브너 기저 공격을 포함한 대수적 공격들은 차분 공격, 선형 공격과 달리 단 하나의 평문/암호문 쌍이 주어지더라도 공격을 수행할 수 있는 경우가 많아서 더 유용하게 쓰일 수 있습니다.

A. 그뢰브너 기저 공격

그뢰브너 기저에 대한 정보는 rbtree님의 글을 참고해주세요.

그뢰브너 기저 공격은 먼저 주어진 암호의 구조를 일종의 다변수 방정식으로 생각합니다. 그 다음 이를 그뢰브너 기저로 변환해 단일 변수 방정식을 얻어내어 풀이를 하는 공격입니다. 예를 들어 Large S-box의 입력으로 $x$가 주어지고 $x^{-1} = y$가 계산되었다고 할 때, 이는 곧 $xy = 1$이라는 식을 의미합니다. 비슷한 방법으로 암호화 과정에서 나오는 여러 중간 변수들의 값들을 미지수로 두고 식을 여러개 세워 그뢰브너 기저 공격을 진행할 수 있습니다.

그뢰브너 기저 공격에 필요한 시간복잡도는 이미 알려져있기 때문에 우리가 만들어낸 암호 체계의 안전한 라운드를 잡기 위해서는 라운드에 따른 만들어낼 수 있는 식의 수와 필요한 변수의 수를 계산하고, 이후 그뢰브너 기저 공격을 진행할 때 시간복잡도가 어떻게 되는지를 확인하면 됩니다. 참고로 Rain에서는 그뢰브너 기저 공격이 가장 위협적인 공격이었고 그 외의 나머지 공격들은 전부 2라운드만 되어도 안전했습니다.

B. Linearization attack

Linearization attack은 그뢰브너 기저 공격과 마찬가지로 주어진 암호 구조에서 얻을 수 있는 모든 식을 쓰는데 이 때 등장하는 모든 monomial들을 별개의 변수로 둬서 선형화를 시키는 공격입니다. 예를 들어 $x^3y + y^2 = 1$, $y^2 + xz^4 = 1$, $x^3y + xz^4 = 0$ 이라는 식이 있다고 해봅시다. 이 식의 해를 구하는건 굉장히 어려운 작업이겠지만 Linearization을 거치기 위해 $x^3y = a$, $y^2 = b$, $xz^4 = c$로 치환할 경우 이 연립방정식은 $a+b=1$, $b+c=1$, $a+c=0$이라는 아주 단순한 형태의 일차연립방정식이 됩니다.

Linearization attack을 성공적으로 수행하기 위해서는 식에 등장하는 monomial의 수와 같거나 더 많은 식을 얻을 수 있어야 합니다. 반대로 말해 식에 등장하는 monomial의 수가 많거나, 반대로 식의 수가 적을수록 Linearization attack은 어려워집니다. Large S-box에 대해 Linearlization attack이 잘 적용될 수 있는지에 대한 연구는 On Exact Algebraic [Non-]Immunity of S-Boxes Based on Power Functions에서 확인 가능합니다.

해당 논문에 따르면 $XY = 1$ 꼴의 식에서 각 비트를 $x_i, y_i$로 둘 때 $x_iy_j$ 꼴의 항이 나오는 선형 독립인 식(bi-affine equation)은 $3n-1$개, $x_ix_j, y_iy_j$ 꼴의 항이 나오는 선형 독립인 식(fully quadratic equation)은 $5n-1$개가 나옵니다. monomial의 수는 대략 $2n^2$개임을 감안할 때 식의 수는 충분히 작아 Linearization attack은 불가능함을 알 수 있습니다.

C. Guess-and-Determine attack

Guess-and-Determine attack은 다른 대수적 공격에서 일부의 비트를 고정해 공격의 복잡도를 낮추는 방법입니다. 이 고정하는 일부의 비트의 길이를 $b$라고 할 때 $O(2^b)$의 전수조사가 필요하게 됩니다. 당연히 키에 대한 직접적인 전수조사보다는 효율적인 공격을 찾기를 원하니 $b < n$이어야 합니다.

Guess-and-Determine attack은 주로 위에서 언급한 그뢰브너 기저 공격 혹은 Linearization attack과 결합해서 쓰일 수 있습니다. 다만 실제로 이 방법이 적용되어 일부 비트를 고정했을 때 대수적 공격의 시간복잡도가 얼마일지를 이론적으로 예측하는건 상당히 어렵습니다. 그렇기 때문에 암호를 설계하는 입장에서는 평문의 변화가 일부 라운드만 거치고 나도 전체로 확산이 되어 Guess-and-Determine이 일정 라운드 이상에서는 의미가 없다는 식의 방어 논리를 도입하는 경우를 종종 볼 수 있습니다.

5. Conclusion

이번 글에서는 Large S-box를 사용한 암호 시스템에 대해 알아보고 Large S-box에서의 차분 공격, 선형 공격, 대수적 공격에 대해 정리해보았습니다. 사실 공격자의 입장에서는 Large S-box가 사용된 암호 시스템을 보면 라운드가 조금만 늘어나도 사실상 공격이 불가능하다고 생각을 할 수 밖에 없습니다. 하지만 설계자의 입장에서는 암호가 안전한 이유를 다른 사람들에게 설득력 있게 설명할 수 있어야 하기 때문에 이 글에서 제시한 것 이상으로 다양한 공격들에 대한 안전성을 따져봐야 합니다.

특히 대수적 공격은 최근에 제시된 LowMC 혹은 MiMC에 대한 공격과 같이 암호 시스템을 공격하는 중요한 기법으로 이용되고 있기 때문에 이번 기회를 통해 익혀두는 것을 추천드립니다.