Bitslice을 활용한 암호 구현

들어가며

이번 글에서는 1997년 Eli Biham의 “A Fast New DES implementation in Software”에서 다시 환기된 Bitslice 기법에 대해서 작성해보려고 합니다. 이전 1970년대에 사용되던 Bitslice는 워드의 길이를 늘리기 위해서 더 작은 bit 너비에서 구성하는 것이었습니다. 현대에 들어서는 거의 사용되지 않았지만, Eli Biham이 평문을 병렬화하여 DES의 고속구현을 하며 소프트웨어단에서 재사용되기 시작했습니다.

현대의 Bitslice기법은 각 단어를 Bit별로 잘라, 여러 단어의 특정 bit들을 묶어 재지정한 다음 연산을 하는 과정을 의미합니다. 그렇게되면, 재지정된 한 단어는 기존 여러 단어들의 동일한 위치의 bit가 되는 것입니다. 아래의 표와 같이, 가로로 원래 단어인 p1 ~ p4 를 배치했을 때, 세로로 읽는 새로운 단어들 new_p1 ~ new_p4 를 이용하여 연산을 하는 것이 Bitslice의 방법입니다.

	new_p1	new_p2	new_p3	new_p4
p1	1	1	1	0
p2	0	1	1	0
p3	1	0	0	1
p4	0	0	1	0

DES implementation with Bitslice

DES는 평문을 치환하는 Initial Permutation 과정을 거친 후 좌측 32bit $L_i$와 우측 32bit $R_i$로 분할됩니다. 각 Round 별로 Key Schedule을 통해 생성되는 key와 $R_i$를 F함수를 통해 연산한 후, 기존의 $L_i$와 xor하여 새로운 $R_{i+1}$를 만들고, 기존의 $R_i$가 $L_{i+1}$가 되는 것의 반복을 통해 암호화됩니다. 각 단계별로 나누어서, 어떻게 Bitslice를 적용하는지 간단하게 알아보겠습니다.

Preprocessing

Bitslice를 통해 암호화를 하기 위해서는 기존의 평문을 Bitslice하여 새로운 단어들로 전처리를 진행해야합니다. n개의 평문이 있을 때, j번째 평문의 i번째 bit가 0인지 1인지에 따라, arr[i]의 j번째 bit를 표기해주면 됩니다. Bit연산자를 이용하면 어렵지 않게 작성할 수 있습니다. 평문의 개수에 따라 Bitslice를 했을 때의 변수 길이가 달라지기 때문에, n의 크기에 맞춰 단어의 크기를 결정할 수 있습니다.

DES는 페이스텔 구조를 갖기 때문에, 전처리의 결과를 L[32]와 R[32]로 나누게 되면 편리합니다.

Key또한 이후 연산에서 xor을 해주기 위해서는 Bitslice를 해주어야 합니다. 위에서 평문을 Bitslice하는 것과 동일하게, Key 또한 slice할 수 있습니다. Key가 일정한 경우에는 각 Bitslice 된 변수들이 0 또는 ~0이 됨을 쉽게 알 수 있습니다.

Key는 Key Schedule을 진행할 때, parity bit 8개를 제외한 뒤 진행하기 때문에, 전처리 단계에서 56개 bit만을 이용하여 만들 수 있습니다.

Initial Permutation and Inverse Permutation

DES에서 제일 처음과 마지막에 수행하는 치환과정입니다. 기존의 방식이라면 평문별로 새롭게 치환된 단어를 만들어야 하겠지만, Bitslice를 이용하는 방법에서는 각 bit의 위치별로 치환해주기만 하면 됩니다. 새로운 배열을 만들어 Initial Permutation, Inverse Permutation에 맞추어 치환한 뒤 옮겨주면 됩니다. 기존의 방식과 연산의 횟수를 비교하였을 때, Bitslice가 n중 병렬 작업이라는 것을 고려하면 상당히 효율적이라고 볼 수 있습니다.

F function

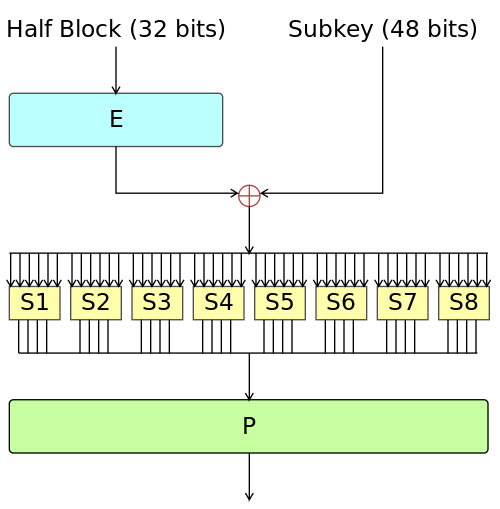
$R_i$를 확장하여 48bit로 만든 뒤, 이를 Key Schedule을 통해 생성된 Round key와 xor한 뒤 Sbox를 통해 치환하고, P permutation을 진행하는 단계입니다. 단계가 많기 때문에, Key schedule과 Sbox는 따로 작성하겠습니다.

먼저 $R_i$의 Expansion의 경우, 앞에서 했던 Permutation과 동일한 방법으로 진행하면 됩니다. $R_i$를 저장하고 있는 R[32]를 이용하여 48개짜리 E[48] 배열로 확장한 뒤, Key schedule을 통해 생성된 Round key와 xor 연산을 하면 됩니다.

기존의 방식과 다르게 데이터를 처리하고 있기 때문에, xor을 하기 위해서는 Round key 또한 bitslice된 상태로 연산할 수 있어야 합니다. i번째 bit가 한 변수에 들어있는 Bitslice의 특성상, Round key의 i번째 bit들을 모아놓은 변수와 xor을 해주어야, 정상적인 연산이 진행되는 것입니다.

전처리로 Key 또한 Bitslice를 해두었고, 다음에 올 Key Schedule에서 Round key를 Bitslice에 맞는 형식으로 제공해주면 각 i번째 변수끼리 xor을 함으로써 정상적인 암호화를 할 수 있습니다.

Key Schedule

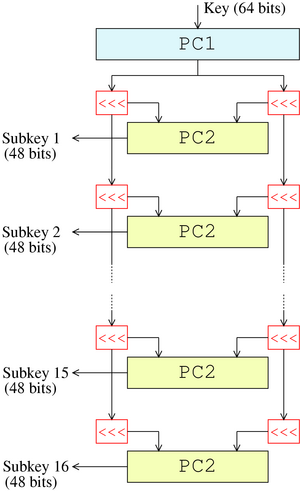
Key Schedule의 경우, 전처리 과정에서 parity bit 8개를 제외하였기 때문에, 왼쪽 28bit와 오른쪽 28bit로 나누어 shift하는 과정과, PC2 치환을 통해 48개의 bit를 정하는 과정만 진행해주면 됩니다.

전처리에서 이미 Bitslice를 해두었기 때문에, 다른 치환과 동일하게 Bit shift는 배열의 위치를 변경하는 것으로 해결할 수 있습니다. 왼쪽으로 1 또는 2 bit만큼 shift하여 Round key를 만들기 때문에, 각 라운드별로 54 또는 52번의 swap을 통해 연산을 shift를 완료할 수 있습니다.

48개의 bit를 골라내 Round key로 만들어주는 과정 또한 Bitslice된 배열에서 48개만을 골라서 새로운 배열을 만들어주면 됩니다.

Sbox

마지막으로 남은 DES의 과정인 Sbox입니다. DES의 암호화 과정 전체 중, Sbox만이 bit연산으로 만들어지지 않는 과정입니다. 그렇기 때문에, 이 부분은 위와 다른 방식을 사용해야 합니다.

Sbox는 총 8개로 이루어져 있는데, 각 Sbox별로 6bit를 이용해 4bit로 치환해내는 과정입니다. 이를 구현하기 위해서, MUX를 이용하였습니다. 출력을 bit별로 나누어서 생각하면, 6개의 bit에 따라 0, 1이 결정되는 것이 총 4개가 있는 것으로 볼 수 있습니다.

6개의 bit를 통해 하나의 bit를 결정되는 과정을 구현하기 위해, 각 입력별 결과를 MUX의 입력으로 설정하고, 6개의 bit들이 MUX의 스위치로 구성하였습니다.

예시로, 다음은 Sbox1의 결과물 중 첫 비트를 만들어내는 함수를 MUX만을 이용하여, 최적화를 거치지 않고 만들어낸 과정 중 일부입니다.

	a[0] = mux(0, ~0, Input[5]);
    a[1] = mux(~0, ~0, Input[5]);
    a[2] = mux(0, 0, Input[5]);
	
    ...

    a[29] = mux(0, 0, Input[5]);
    a[30] = mux(0, 0, Input[5]);
    a[31] = mux(~0, 0, Input[5]);

Sbox의 결과물의 첫 bit가 0인지 1인지에 따라 mux의 값으로 0 또는 ~0이 들어가고, 스위치로 Sbox에 사용되는 6bit 중 마지막 bit를 사용하였습니다. 이 뒤부터는, 기존의 결과물들을 이용하여 mux를 반복하여, 총 하나의 결과물을 만들어내는 과정입니다.

    b[0] = mux(a[0], a[1], Input[4]);
    b[1] = mux(a[2], a[3], Input[4]);
    b[2] = mux(a[4], a[5], Input[4]);
    b[3] = mux(a[6], a[7], Input[4]);
    b[4] = mux(a[8], a[9], Input[4]);
    b[5] = mux(a[10], a[11], Input[4]);
    b[6] = mux(a[12], a[13], Input[4]);
    b[7] = mux(a[14], a[15], Input[4]);
    b[8] = mux(a[16], a[17], Input[4]);
    b[9] = mux(a[18], a[19], Input[4]);
    b[10] = mux(a[20], a[21], Input[4]);
    b[11] = mux(a[22], a[23], Input[4]);
    b[12] = mux(a[24], a[25], Input[4]);
    b[13] = mux(a[26], a[27], Input[4]);
    b[14] = mux(a[28], a[29], Input[4]);
    b[15] = mux(a[30], a[31], Input[4]);

    c[0] = mux(b[0], b[1], Input[3]);
    c[1] = mux(b[2], b[3], Input[3]);
    c[2] = mux(b[4], b[5], Input[3]);
    c[3] = mux(b[6], b[7], Input[3]);
    c[4] = mux(b[8], b[9], Input[3]);
    c[5] = mux(b[10], b[11], Input[3]);
    c[6] = mux(b[12], b[13], Input[3]);
    c[7] = mux(b[14], b[15], Input[3]);

    d[0] = mux(c[0], c[1], Input[2]);
    d[1] = mux(c[2], c[3], Input[2]);
    d[2] = mux(c[4], c[5], Input[2]);
    d[3] = mux(c[6], c[7], Input[2]);

    e[0] = mux(d[0], d[1], Input[1]);
    e[1] = mux(d[2], d[3], Input[1]);

    output[0] = mux(e[0], e[1], Input[0]);

이러한 과정들을 Sbox별로 4번, 8개의 Sbox에 대해 진행해주면 됩니다. 이 코드의 경우, 최적화가 되어있지 않기 때문에 상당히 많은 양의 연산을 필요로 합니다.

mux는 3번의 bit 연산을 필요로 하고, 8개의 Sbox 연산에서 각 bit별로 63번의 mux를 호출하였습니다. 계산을 통하면, 총 1512번의 bit 연산을 통해 Sbox 과정을 마무리했다고 볼 수 있습니다.

이 코드는 최적화가 되지 않은 코드이기 때문에, mux를 줄이는 방법을 통해 최적화를 할 수 있습니다. 여러 논문들을 확인하면, 각 Sbox별로 60~100번의 연산을 통해 만들어낼 수 있다는 결과를 볼 수 있었습니다.

결론

제가 작업한 DES의 경우, unsigned long long을 이용하여 64중 병렬 연산을 할 때, Apple Silicon M1 기준 기존 DES에 비해 4~4.5배 정도의 효과를 얻을 수 있음을 확인하였습니다.

제가 작성한 두 DES 코드가 최적화가 된 것은 아니기 때문에 정량적인 비교라고 할 수는 없으나, 유의미한 속도의 차이가 남을 확인할 수 있습니다.

Bitslice를 이용한 DES 암호화 과정에서 Sbox가 상당한 연산 비중을 차지하고 있기 때문에, 연산을 최소화할 경우 더욱 효과적으로 시간을 줄일 수 있습니다.

이 방식을 통하여 AES 또한 암호화가 가능하며, 현재 후양자 암호인 RAINBOW signature scheme의 Level 1도 Bitslice를 이용하여 구현되어 있습니다.

또 다른 장점

기존의 DES, AES에서 Sbox는 look-up table 방식을 통해 계산하였기 때문에, Cache timing attack을 당할 수 있습니다. 그러나 Bitslice를 이용한 암호화의 경우, 어떤 평문과 키를 통해 암호화하더라도 동일한 연산량이 요구됨을 암호화 과정을 통해 알 수 있습니다.

단점

Bitslice의 단점은 Sbox의 최적화에 따라 속도가 급격하게 바뀐다는 점과, 병렬로 암호화를 진행하기 떄문에 암호 운용 방식에 있어서 제약이 생긴다는 점입니다. ECB 형식으로 운용하는 경우는 거의 없기 때문에, CTR 방식을 확장시켜 운용하는 방법뿐이 없다는 점입니다.

참고 자료

Eli Biham. A Fast New DES Implementation in Software
Emilia Käsper, Peter Schwabe. Faster and Timing-Attack Resistant AES-GCM