Euler Tour 테크닉
문제 상황
다음과 같은 문제를 생각해 보자.
(루트가 있는) 트리 $T$가 있다. 모든 정점은 초기에 $0$의 가중치를 가지고 있다. 이 때, 다음 두 종류의 질의를 처리해보자.
- 정점 $v$와 새로운 가중치 $x$가 입력으로 주어질 때, 정점 $v$의 가중치를 $x$로 바꾼다.
- 정점 $x$와 $x$의 모든 후손들(즉, 정점 $x$를 루트로 한 부트리의 정점들)의 가중치의 합을 구한다.
생각할 수 있는 가장 쉬운 풀이들은
- $arr[x]$를, 정점 $x$의 가중치로 정의한다. 1번 질의는 상수 시간에 처리할 수 있다. 2번 질의에서 일일히 정점 $x$의 후손들을 순회하며 가중치를 합한다.
- $arr[x]$를, 정점 $x$의 모든 후손들의 가중치의 합(2번 질의의 답)으로 정의한다. 1번 질의에서 일일히 정점 $x$의 조상들을 순회하며 $arr$ 값을 업데이트해준다. 2번 질의는 상수 시간에 처리할 수 있다.
이다. 두 풀이 모두 한 질의를 상수 시간에 처리하는 대신 다른 질의에게 계산량을 떠넘긴다. 적절한 전처리를 통해 두 질의의 계산량을 균형있게 줄이는 방법이 필요하다. 배열에서 이와 비슷한 문제를 해결하는 자료구조인 세그먼트 트리를 떠올리는 과정과 유사하게 느껴진다. 실제로 이 문제는 세그먼트 트리를 응용한 방법으로 해결할 수 있다.
Euler Tour 테크닉
트리를 적절히 펴서 배열에 저장한다고 생각해보자.
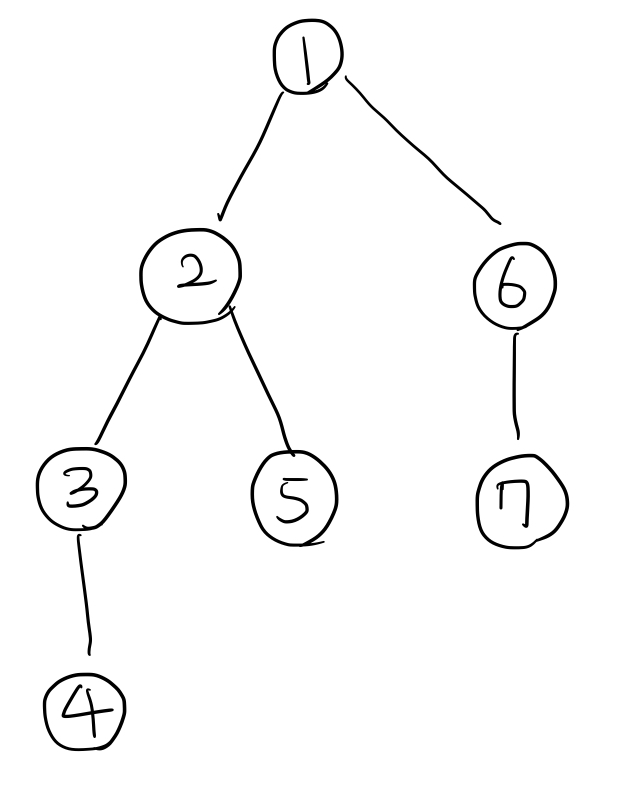
위 그림과 같은 트리에서, 루트에서부터 DFS를 수행한다고 생각해보자. 아래는 가장 단순한 DFS의 코드이다.
vector<int> childs[MAX_V];
void dfs(int x) {
for (int y : childs[x]) {
dfs(y);
}
}
루트인 1번 정점에서부터 시작해, 2, 3, 4번 정점을 순서대로 방문한 다음, 반대로 3, 2번 정점으로 돌아오고 나서, 5번 정점을 방문한 다음 다시 2, 1번 정점으로 돌아온다. 다음, 6번 정점을 방문하고, … 와 같은 순서로 정점들을 방문하게 된다.
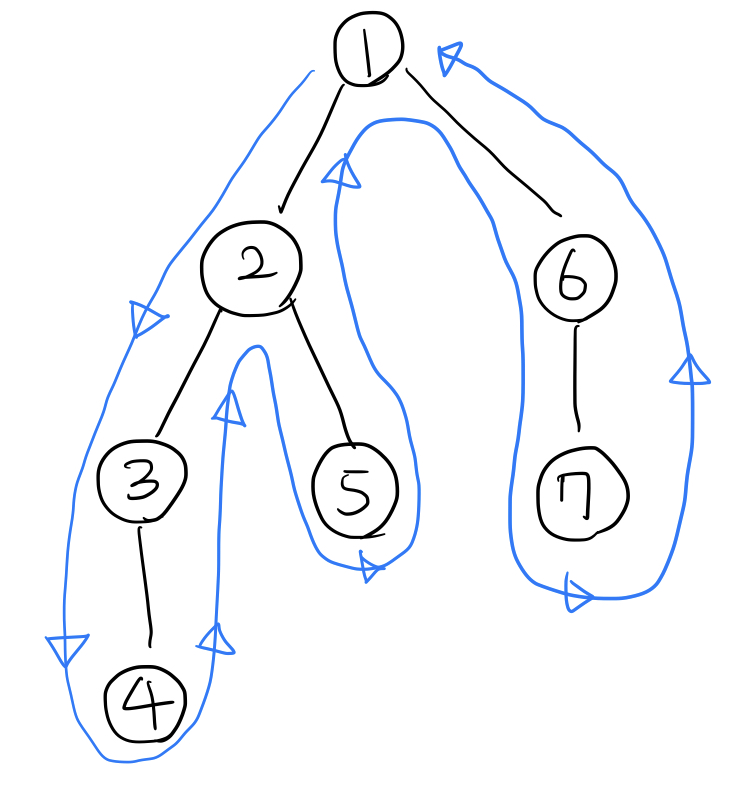
DFS에서 각 정점에 1) 들어가고, 2) 나가는 순서를 기록해보자.
1번 정점 들어감 $\rightarrow$ 2번 정점 들어감 $\rightarrow$ 3번 정점 들어감 $\rightarrow$ 4번 정점 들어감 $\rightarrow$ 4번 정점 나감 $\rightarrow$ 3번 정점 나감 $\rightarrow$ 5번 정점 들어감 $\rightarrow$ 5번 정점 나감 $\rightarrow$ 2번 정점 나감 $\rightarrow$ 6번 정점 들어감 $\rightarrow$ 7번 정점 들어감 $\rightarrow$ 7번 정점 나감 $\rightarrow$ 6번 정점 나감 $\rightarrow$ 1번 정점 나감
이를 기록하기 위해, DFS 코드에 ‘순서’를 표시하는 cnt 변수를 추가해보자. cnt 변수는 정점에 들어갈 때마다 하나씩 증가하며, DFS에서 정점 $x$에 들어가는 시점의 cnt 값은 in[x]에, 나가는 시점의 cnt 값은 out[x]에 저장된다.
vector<int> childs[MAX_V];
int in[MAX_V], out[MAX_V];
void dfs(int x) {
cnt++;
in[x] = cnt;
for (int y : childs[x]) {
dfs(y);
}
out[x] = cnt;
}
정점에서 나갈 때에는 cnt 변수를 증가시키지 않았음에 주목하라. 증가시키도록 할 수도 있지만, 그렇지 않았을 때와 완전히 동일한 구현이 된다.
‘DFS에서 정점에 들어가는 시점’에 cnt를 하나씩 증가시켰다. DFS가 끝나고 나면 cnt는 정점의 개수와 같게 된다. 위 예시 트리에서 각 정점의 in, out 값은 다음 표와 같다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
in |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
out |
7 | 5 | 4 | 4 | 5 | 7 | 7 |
이제, 각 정점은 in[x]부터 out[x]까지의 ‘구간’으로 나타나게 된다. 게다가 여기서 정점 $x$의 후손들이 나타내는 구간은, 모두 정점 $x$가 나타내는 구간에 포함된다. 이는 DFS 과정을 생각하면 자명하다. DFS에서는 정점 $x$에 들어간 다음에 $x$의 후손 정점에 들어가게 될 것이고, $x$의 후손 정점에서 나간 다음에야 정점 $x$에서 나가게 될 것이기 때문이다. 구간의 포함관계로 트리를 묘사한 것이다.
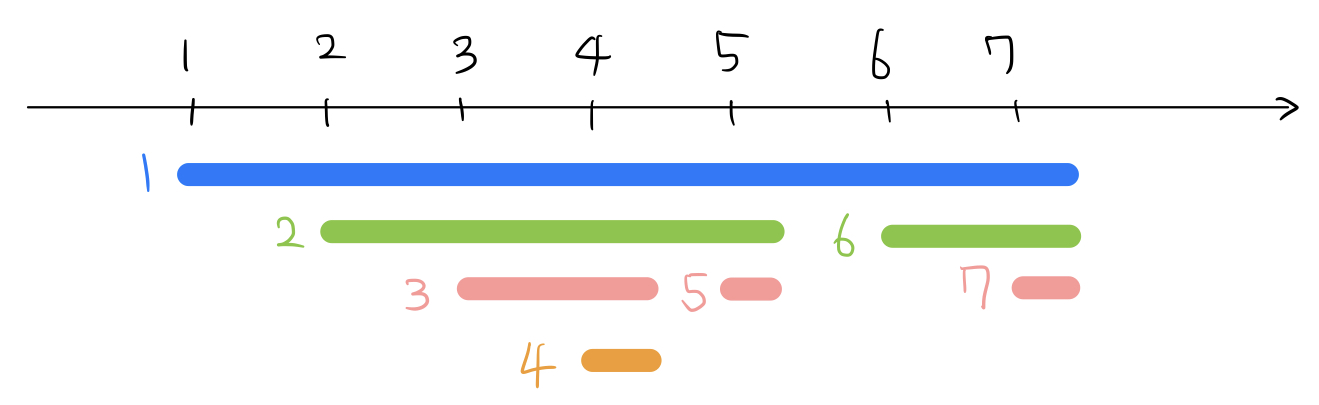
이 성질을 이용하면, 세그먼트 트리를 이용해 문제 상황을 해결하는 원리를 이해할 수 있다. 위 수직선 위에 세그먼트 트리를 올려둔다고 생각해보자.
- 가중치 변경 질의:
in[x]번 인덱스의 원소를 바꾼다. - 후손들의 가중치의 합 질의:
in[x]번 인덱스부터out[x]번 인덱스까지의 원소의 합을 구한다.
in[x]부터 out[x]까지에 정점 $x$의 후손들이 모두 포함되어있기 때문에 2번 질의의 결과 후손들의 가중치의 합을 얻을 수 있다. 질의의 시간 복잡도는 세그먼트 트리와 같은 $O(\log N)$ ($N$은 정점의 개수) 이다. 완성된 코드는 아래 응용 문단의 ‘회사 문화 3’ 문제를 참조하라.
위와 같이, 트리의 각 정점을 DFS의 방문 순서에 따라 배열의 원소 또는 구간으로 대응시켜 문제를 푸는 방법을 Euler Tour 트릭, 또는 Euler Tour 테크닉이라고 불린다. 각 간선을 한 번씩 방문하는 회로를 의미하는 Euler Circuit과 달리, 트리에서의 DFS에서는 각 정점을 (들어올 때와 나갈 때 한 번씩) 두 번 방문한다. Euler Tour가 아니기 때문에, 대신에 DFS Ordering 테크닉 등의 이름을 붙이는 것이 더 적확하게 느껴진다. 그럼에도 이 기법은 흔히 Euler Tour 테크닉이라고 불린다.
응용
회사 문화 3 (#)
‘회사 문화’ 시리즈는 이와 같은 테크닉을 연습할 수 있는 좋은 문제들로 이루어져 있다. 문제의 지문이 썩 직관적이지 않아 요약하면 다음과 같다.
- 회사는 상사 <-> 부하 관계로 이루어진 트리이다.
- 사원을 $x$만큼 칭찬하면 그 사원을 포함해 사원의 (직속) 상사, 상사의 상사, 상사의 상사의 상사, …의 ‘칭찬 수치’가 $x$ 만큼 증가한다. (모든 직원의 초기 칭찬 수치는 0이다.)
- 이 때, (1) 사원을 $x$만큼 칭찬하는 질의 (2) 사원의 ‘칭찬 수치’를 구하는 질의 를 처리하는 문제이다.
문제를 이해한 다음 약간의 사고과정을 거치면 위 예시 문제와 같은 문제가 된다는 것을 알 수 있다. 세그먼트 트리 부분을 제외한 코드는 다음과 같다. 아래 코드에서
- 초기에 모든 원소는 0으로 초기화되어 있다.
update(i, k):i번째 인덱스의 원소에k를 더한다.query(x, y):x번째 인덱스부터y번째 인덱스까지의 합을 구한다.
를 지원하는 세그먼트 트리의 코드를 추가하면 문제를 풀 수 있다.
int V, Q, p[MAXV], in[MAXV], out[MAXV];
vector<int> childs[MAXV];
int cnt = 0;
void dfs(int x) {
cnt++;
in[x] = cnt;
for (int y : childs[x]) dfs(y);
out[x] = cnt;
}
int main() {
cin >> V >> Q;
for (int i=1; i<=V; i++) {
cin >> p[i];
if (p[i] > 0) childs[p[i]].push_back(i);
}
dfs(1);
for (int i=0; i<Q; i++) {
int q, x, y;
cin >> q;
if (q == 1) {
cin >> x >> y;
t.update(in[x], y);
}
if (q == 2) {
cin >> x;
cout << t.query(in[x], out[x]) << '\n';
}
}
}
코드의 길이가 매우 짧음에 비해 아주 폭넓게 응용할 수 있다.
회사 문화 2 (#)
‘회사 문화 3’과 방향이 반대로 되어있는 문제이다. 하지만 ‘회사 문화 3’과 같은 형태로 생각하면 풀 수 있다. 정점 $x$를 칭찬하면 영향을 받는 대상은 $x$와 $x$의 모든 후손들이다. 트리의 DFS order를 계산해서 in, out 배열을 완성하면,
- 1번 질의: 배열의
in[i]번째부터out[i]번째까지의 원소를w만큼 증가시킨다. - 2번 질의: 배열의
in[i]번째 원소를 출력한다.
로 해석할 수 있다. 1번 질의가 위와 같이 해석될 수 있는 것에는, “트리의 각 정점과 배열의 각 원소가 일대일 대응”된다는 사실이 이용되었다. 우리는 트리의 $1$번부터 $N$번까지의 각 정점을 배열의 원소 하나씩에 대응하는 데에만 집중했다. 하지만 결과 만들어진 배열의 길이 또한 $N$이기 때문에, 거꾸로 배열의 각 원소도 정확히 한 개의 정점에 대응되게 된다.
회사 문화 5 (#)
같은 방식으로 각 질의를 다음과 같이 해석할 수 있다.
- 1번 질의: 배열의
in[i]번째부터out[i]번째까지의 원소를 $1$로 만든다. - 2번 질의: 배열의
in[i]번째부터out[i]번째까지의 원소를 $0$으로 만든다. - 3번 질의: 배열의
in[i]번째부터out[i]번째까지의 원소들 중 $1$의 개수를 출력한다.
이는 느리게 갱신되는 세그먼트 트리를 이용해 해결할 수 있다. 느린 갱신과 같이 세그먼트 트리에 사용되는 다양한 기법들 뿐 아니라 평방분할 등 다양한 기법과 자료구조들을 Euler Tour 테크닉과 함께 적용할 수 있다.
트리와 XOR 쿼리 (#)
문제가 아주 복잡해 보이지만, XOR 연산의 가장 중요한 성질 “같은 원소를 XOR하면 0이 된다”를 이용하면 Euler Tour 테크닉을 사용할 수 있는 꼴로 바꿀 수 있다. Euler Tour 테크닉은 모든 질의들이 다음과 같은 형태일 때 효과적으로 사용할 수 있다.
- 정점 $x$의 모든 후손에 대해 어떤 연산을 실행한다.
- 정점 $x$의 모든 조상에 대해 어떤 연산을 실행한다. (이는 보통 1.과 같은 형태로 바꿀 수 있다.)
위와 같은 형태로 문제의 2번 질의를 바꾸어 보자. $d(x, y) = d(x, 1) \oplus d(y, 1)$ 을 이용하자. 각 정점 $x$에 대해 $d(x, 1)$, 즉 이 정점에서 루트 정점까지 모든 간선의 가중치를 XOR한 값을 관리하자. 그러면 1번 질의는, 정점 $x$의 모든 후손 $z$에 대해 $d(z, 1)$을 바꾸는 연산이 된다. 새로운 $d(z, 1)$은 원래의 $d(z, 1)$에 $v$를 XOR한 값이 된다.
이는 2번 질의를 해결하기에 충분하지 않다. 정점 $x$에 대해, “$x$와 $x$의 모든 후손들 $z$에 대해, $d(z, 1)$의 목록”을 가지고 있어야 한다. 여기서 ‘각 비트가 켜져있는 $d$값이 몇 개인지’가 중요하다.
- $arr[x][i]$ : $x$와 $x$의 모든 후손들 $z$에 대해, $d(z, 1)$는 0 이상의 정수이다. 여기서 $i$번째 비트가 켜져있는 것의 개수
으로 정의하자. 이와 같이 정점마다 20 (가중치 값의 비트의 개수)개의 원소를 관리하는 세그먼트 트리 (또는 20개의 세그먼트 트리도 가능하다)를 만들면 2번 질의 또한 위 문제들과 다르지 않은 방법으로 해결할 수 있게 된다.
정리
Euler Tour 테크닉에서 사용했던 트리를 직선으로 ‘펴자’는 아이디어는, ‘트리의 정점을 수직선의 구간으로 표현한다’는 아이디어로 연결된다. 이런 사고의 전환은 ‘정점 $x$의 후손에 대해 어떤 연산을 실행’하는 쿼리 문제들 뿐 아니라, 트리와 관련된 문제들에서 자주 유용하게 사용될 수 있다. 예를 들어, ‘$x$를 나타내는 지점과 $y$를 나타내는 지점을 모두 포함하는 최소의 구간’이 두 정점의 LCA가 된다는 성질을 이용해 해결할 수 있는 문제도 있다.