antemrdm's profile image

antemrdm

August 21, 2022 00:00

Word embedding and Word2Vec Analysis

Introduction

컴퓨터가 다루는 정보의 종류는 정말 다양하지만, 대부분의 정보는 모두 수로 표현할 수 있습니다. 이미지도 픽셀값으로 표현이 되고 언어도 인코딩되어 숫자로 표현됩니다. 원래 수의 형태로 존재하는 정보들은 서로 값이 유사할수록 가까운 관계이고, 차이가 클수록 서로 먼 관계일 것입니다. 하지만 언어의 경우 인코딩된 결과값이 유사하다고 해서 서로 가까운 관계라는 보장이 없습니다. 하나의 예로 ASCII code를 살펴보겠습니다. !, A, B, a는 각각 33, 65, 66, 97의 ASCII code에 해당합니다. A와 B의 차이가 1이고, A와 a의 차이가 32입니다. 물론 관점이나 목적에 따라 다를 순 있겠으나, A와 a 간의 관계가 A와 B 간의 관계보다 32배 멀다고 볼 수는 없을 것입니다. 심지어 !와 A 간의 차이와 A와 a 간의 차이가 동일합니다. 따라서 ASCII code를 통해 문자를 숫자로 변환할 때 서로 간의 유사도를 반영하지 않습니다.

하지만 인공지능 분야에 있어서 현재의 트렌드가 Representation learning인 만큼, 데이터의 표현 방식의 중요성이 주목받고 있습니다. 어떠한 task를 수행함에 있어서 정보를 어떻게 표현하느냐가 해당 task의 난이도와 성능에 큰 영향을 줍니다. 이러한 관점에서 자연어, text 데이터를 어떻게 표현할 것인지에 관한 많은 연구가 이루어졌고, 이 글에서는 그 중에서도 단어를 어떻게 벡터로 잘 표현할 것인가에 대해 알아보겠습니다.

Word embedding

Word embedding이란 단어를 벡터의 형식으로 표현하는 것을 의미합니다. 단어를 벡터로 변환하는 방법에는 다양한 방법이 있습니다. 단순하게는 각 단어 당 하나의 자연수를 할당하는 방법이나 one-hot vector로 표현하는 방법 등이 있을 것입니다. 여기서 one-hot vector란, 단어가 W 개 있을 때 각 단어를 하나의 차원만 1의 값을 가지고 나머지는 0의 값을 가지는 W 차원의 벡터로 표현하는 것을 의미합니다. 이때 문제점은 차원의 수가 단어의 수와 동일하여 매우 크다는 점입니다. 공간의 관점에서 상당히 비효율적입니다. 따라서 word embedding을 할 때는 one-hot vector와 같은 sparse representation이 아닌 dense (distributed) representation으로 표현합니다.

dense (distributed) representation이란 ‘비슷한 문맥에서 등장하는 단어들은 비슷한 의미를 가진다’는 distributional hypothesis이라는 가정 하에 만들어진 표현 방법입니다. 결국 비슷한 의미를 가지는 유사한 단어들을 벡터화할 때 유사한 벡터값을 가지도록 하는 것이 이 방법론의 목적입니다. word embedding을 통해 나온 dense vector를 embedding vector라고 하며, 이러한 표현 방법으로 단어를 표현한다면 embedding vector 간의 유사도를 계산할 수 있다는 점에서 큰 의미를 갖습니다. word embedding에 관련해서는 LSA, Word2Vec, FastText, Glove 등의 다양한 방법론이 존재합니다. 이 글에서는 Word2Vec이라는 방법론에 대해 다루고자 합니다.

Word2Vec

Word2Vec의 목적은 앞서 언급한 것처럼 비슷한 의미를 가지는 유사한 단어들을 벡터화할 때 유사한 벡터값을 가지도록 하는 것입니다. 예를 들면 아래와 같습니다.

  • 한국 - 서울 + 도쿄 = 일본
  • 박찬호 - 야구 + 축구 = 호나우두

위 예시들은 embedding vector가 각 단어의 의미를 내포하고 있음을 의미합니다. Word2Vec의 학습 방식에는 CBOW (Continuous Bag of Words)와 Skip-Gram 두 가지 방식이 있는데 각각에 대해 자세히 알아보도록 하겠습니다.

CBOW (Continuous Bag of Words)

CBOW 방식은 주변에 있는 단어들을 입력으로, 중간에 있는 단어들을 추론하는 방식입니다. 다시 말해, context (맥락)으로부터 center (target)을 추론하는 방식이라고 볼 수 있습니다. 예를 들어, “The fat cat sat on the mat” 이라는 문장이 있을 때, [‘The’, ‘fat’, ‘cat’, ‘on’, ‘the’, ‘mat’] 으로부터 “sat”을 추론하도록 학습합니다. 여기서 추론의 대상이 되는 단어 (”sat”)를 center word라고 하며, 추론에 사용되는 다른 단어들을 context word라고 합니다. 또한 center word를 추론하기 위해 사용되는 context word의 범위를 window라고 하는데 center word의 앞, 뒤로 window 만큼의 context word가 사용되기 때문에, 총 (2 * window) 만큼의 context word가 사용됩니다.

CBOW 방식으로 학습시키기 위한 dataset


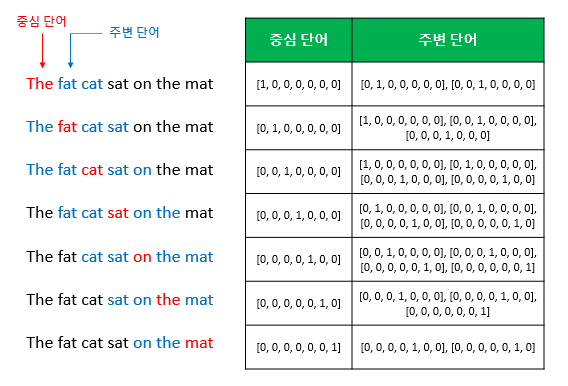
https://wikidocs.net/22660

CBOW 방식으로 학습하기 위해 필요한 dataset은 위 그림과 같이 sliding window 방식으로 만들어집니다. Word2Vec의 input이 되는 center word와 context word가 one-hot vector로 표현됩니다. Word2Vec의 목적이 one-hot vector가 아닌 dense vector로 단어를 표현하는 것이기에 Word2Vec의 input으로는 one-hot vector가 사용될 수 밖에 없습니다.

CBOW 방식에서 사용되는 신경망


https://wikidocs.net/22660

CBOW 방식에서는 hidden layer가 1개인 얕은 신경망(shallow neural network)이 사용됩니다. 일반적인 hidden layer와 달리 activation function이 존재하지 않으며 projection layer라고 부르기도 합니다. 여기서 projection layer의 크기 M이 embedding vector의 차원이 됩니다. 즉 단어들은 어떤 차원의 벡터로 embedding할 것이냐에 따라 projection layer의 차원이 결정됩니다.

Word2Vec의 학습이란 결국 W와 W’을 학습하는 과정입니다. W, W’은 transpose 관계가 아닌 서로 독립적인 행렬이지만 학습이 잘 되었다면 서로 유사한 값을 가지게 될 것입니다.

Input layer (W 행렬)


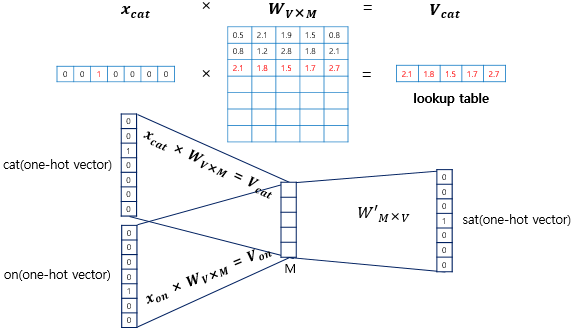
https://wikidocs.net/22660

input layer의 input으로 들어오는 vector는 one-hot vector이기에, 결국 input vector에 i번째 index가 1이라면 input layer의 output은 W의 i번째 row가 됩니다. 이는 W의 i번째 row를 그대로 lookup하는 것과 동일한 동작입니다. 따라서 W는 모든 단어들의 embedding vector이 저장된 lookup table이라고 볼 수 있습니다.

Projection layer (W’ 행렬)


https://wikidocs.net/22660

모든 context word의 one-hot vector에 W를 곱한 결과의 평균이 projection layer의 output이 됩니다. projection layer의 output은 W’와 곱해진 후, softmax 함수를 거쳐 그 결과가 center vector의 one-hot vector와 비교됩니다. 이때 loss function으로 아래 식과 같은 cross entropy가 사용됩니다.

$cost(\hat{𝑦}, y) = -\sum_{j=1}^{V}y_{j}\ log(\hat{𝑦_{j}})$

Output (embedding vector)

W의 각 row를 embedding vector로 사용하거나, W와 W’ 모두를 가지고 (둘의 평균을 내는 등) embedding vector를 계산하기도 합니다. 학습이 잘 되었다면, W와 W’는 유사한 값을 가지기 때문입니다.

Skip-Gram

Skip-Gram 방식은 CBOW 방식과는 반대로, 중간에 있는 단어들을 입력으로 주변 단어들을 추론하는 방식입니다. 따라서 CBOW 방식에서 사용되는 dataset을 사용하는 것은 동일하지만 input으로 center word의 one-hot vector가 사용된다는 점이 차이점입니다.

Skip-Gram 방식에서 사용되는 신경망


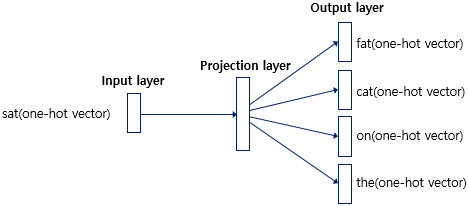
https://wikidocs.net/22660

center word의 one-hot vector를 input layer의 input으로 넣으면, output으로 M 차원의 vector가 출력됩니다. input layer의 output인 M 차원의 vector는 projection layer의 input으로 들어갑니다. projection layer에서 one-hot vector와 같은 차원 (= V)의 output이 나오고, 그 결과를 softmax한 값이 center word의 one-hot vector와 비교됩니다. 여러 논문에서 성능 비교를 진행했을 때 전반적으로 Skip-gram이 CBOW보다 성능이 좋다고 알려져 있습니다.

Negative sampling

실제로 Word2Vec이 위와 같은 방식으로 훈련되지 않고, 추가적으로 고려할 사항들이 존재합니다. word의 수 (= V)가 많아지면 W, W’의 크기인 V*M이 커지고, 역전파 시 계산양이 상당합니다. 이를 개선하는 방법 중 하나가 Negative sampling입니다.

가장 주요한 개념은 기존의 multilabel classification과 유사했던 문제를 binary classification 문제로 변환하는 것입니다. Skip-Gram 방식은 center word를 input으로 넣고 context word를 추론하는 task였습니다. 이를 아래와 같이 center word와 context word를 동시에 input으로 넣고, 두 단어가 실제로 이웃 관계일 확률을 예측하는 task로 바꿉니다. 이렇게 task를 변환함으로써 계산양을 줄일 수 있습니다.


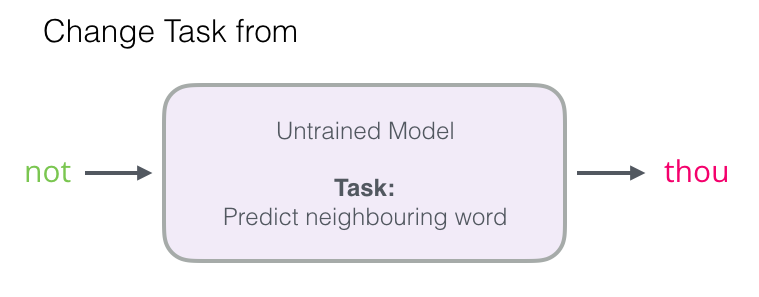
https://jalammar.github.io/illustrated-word2vec


https://jalammar.github.io/illustrated-word2vec

Model

model은 이전과 마찬가지로 2개의 행렬이 됩니다. 하지만 두 행렬 모두 V * M의 형태를 가지고 있습니다. center word를 input으로 하는 행렬을 embedding matrix, context word를 input으로 하는 행렬을 context matrix라고 합니다.


https://jalammar.github.io/illustrated-word2vec

Dataset

task가 바뀌었으므로 dataset도 수정되어야 합니다. 아래와 같이 원래 center word → context word로 mapping된 dataset을 (center word, context word) → 1로 변경합니다.


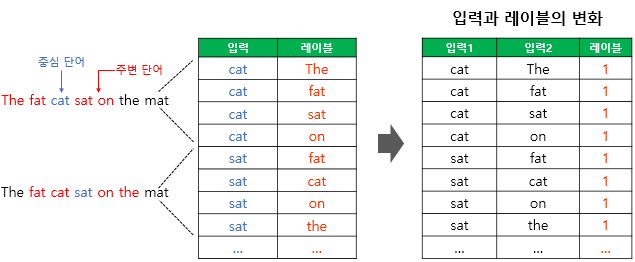
https://wikidocs.net/69141

위와 같이 dataset을 변경하면 model은 항상 1을 출력할 것입니다. 따라서 아래와 같이 negative sample을 추가해야 합니다.


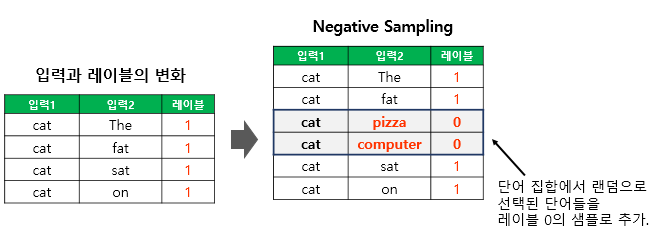
https://wikidocs.net/69141

이때 negative sample로 사용될 word는 기존의 context word가 아닌 다른 모든 word들에서 random하게 선택됩니다. (일종의 noise) 여기서 각 center word 당 사용할 negative sample의 양은 hyperparameter가 되는 것입니다.

학습

하나의 (center word, context word) 쌍이 model의 input으로 들어오면, embedding matrix에서 center word에 해당하는 row, context matrix에서 context word에 해당하는 row를 look up 합니다.


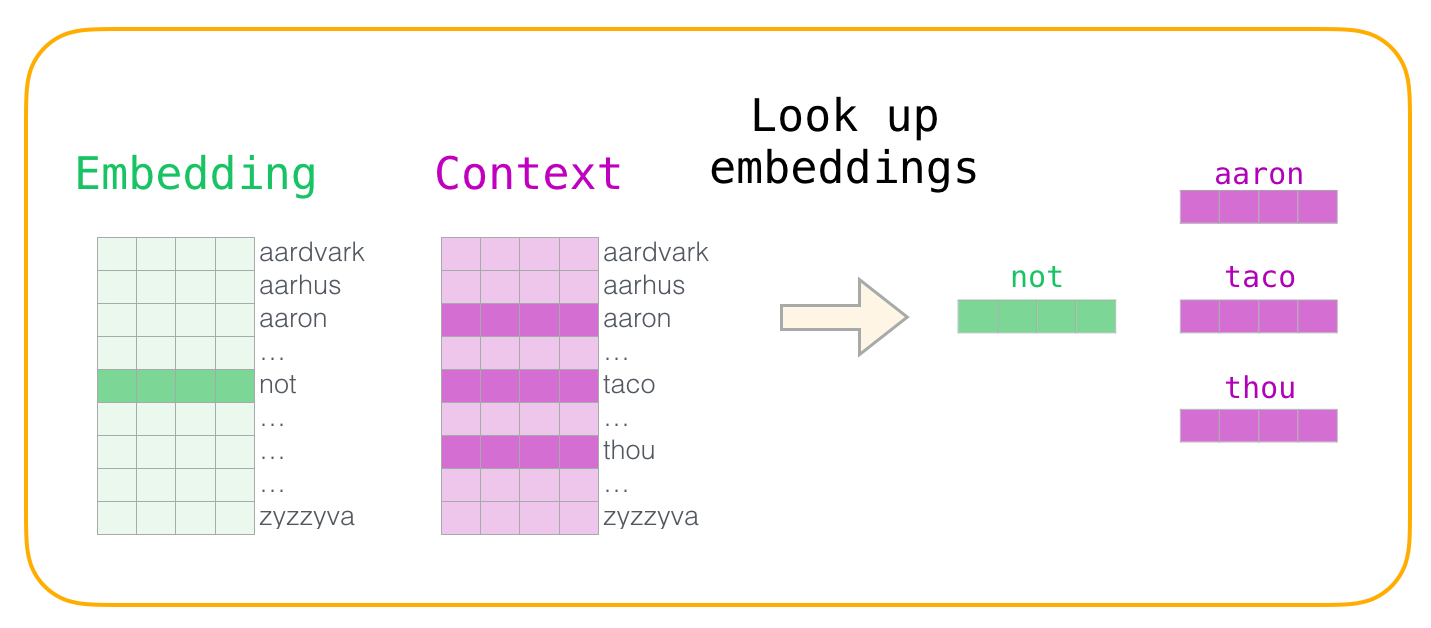
https://jalammar.github.io/illustrated-word2vec

look up된 row들 간의 내적을 구하고, 값의 범위를 (0~1)로 바꾸기 위해서 sigmoid를 취합니다.


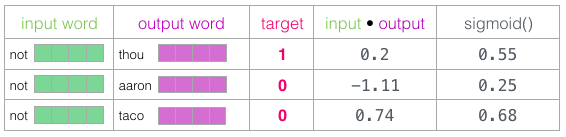
https://jalammar.github.io/illustrated-word2vec

(target label - sigmoid 값)을 error로 보고, 해당되는 row들을 update합니다.


https://jalammar.github.io/illustrated-word2vec

기존의 model처럼 matrix 2개 전체에 역전파하는 것이 아닌, 각 center word에 대해서 context word와 negative sample에 해당하는 row만 update하기 때문에 계산량이 상당히 줄어듭니다.

embedding matrix의 각 row를 embedding vector로 사용할 수도 있고, embedding matrix와 context matrix를 concatenate한 후, 해당 matrix의 각 row를 embedding vector로 사용할 수도 있습니다.

Hyperparameters: window size and number of negative samples

hyperparameter로는 window size와 negative sample의 수, 2가지가 있습니다.

  • window size (여기서는 center word를 중심으로 양쪽의 window를 모두 더한 크기를 의미)


    https://jalammar.github.io/illustrated-word2vec

    • 2 ~ 15 정도의 작은 window size
      • 유사한 embedding vector를 가지는 두 단어가 서로 교환 가능 (interchangeable)한 방향으로 학습합니다.
      • 이때 반의어 또한 interchangeable하다는 사실에 유의해야 합니다.
      • 예를 들어, good이나 bad는 유사한 위치에 등장합니다.
    • 15 ~ 50 정도의 큰 window size
      • 유사한 embedding vector를 가지는 두 단어가 서로 관련성 (relatedness )이 높아지는 방향으로 학습합니다.

Gensim에서는 default window size가 5입니다. (1개의 center word를 사이에 두고 앞뒤로 2개씩의 context word가 존재) 링크를 참고하시면 자세한 사항을 확인하실 수 있습니다.

  • number of negative samples
    • 논문에서는 작은 dataset에 대해서는 5 ~ 20가 유용하게 사용되며, 큰 dataset에서는 2 ~ 5 정도로도 충분하다고 언급합니다.

Gensim에서의 default 값은 5입니다.

GENSIM을 활용한 Word2Vec 구현 및 분석

구현

GENSIM을 활용하여 Word2Vec를 구현해보았습니다. Dataset은 한국어 wiki 문서들을 사용하였습니다.

코드는 https://github.com/junhyeog/gensim-word2vec-kowiki에서 확인하실 수 있습니다.

분석

학습 알고리즘, window size, negative sample의 수에 따른 성능 분석을 위한 실험을 진행하였습니다. 유사도 분석의 기준으로 사용한 단어는 “깜짝”입니다.

총 10개의 실험을 진행했으며 그 결과는 아래와 같습니다. sg가 0이면 CBOW로 학습한 것이고 1이면 Skip-Gram으로 학습한 것입니다. window는 window size를 의미하고 negative는 negative sample의 수를 의미합니다.

[0] sg: 0, window: 5, negative: 10
놀란다       : 0.557
무심코       : 0.551
뭔가        : 0.55
어쩐지       : 0.546
매번        : 0.545

[1] sg: 0, window: 15, negative: 10
놀란다       : 0.642
장난        : 0.626
뭔가        : 0.621
해한다       : 0.611
정말        : 0.605

[2] sg: 0, window: 30, negative: 10
해한다       : 0.623
정말        : 0.61
멋진        : 0.608
놀랐        : 0.608
뭔가        : 0.608

[3] sg: 1, window: 5, negative: 10
놀랬        : 0.796
터뜨린다      : 0.732
어리둥절      : 0.731
열받        : 0.731
어김없이      : 0.718

[4] sg: 1, window: 15, negative: 10
놀랬        : 0.794
긴가민가      : 0.779
울컥        : 0.773
놀랐        : 0.771
오랜만       : 0.76

[5] sg: 1, window: 30, negative: 10
오랜만       : 0.819
울컥        : 0.794
그리웠       : 0.787
정말        : 0.783
은데요       : 0.777

[6] sg: 1, window: 15, negative: 0
문무        : 0.421
소완규       : 0.411
배닝        : 0.405
포강        : 0.403
김석휘       : 0.399

[7] sg: 1, window: 15, negative: 2
글썽이       : 0.766
울먹이       : 0.762
시큰둥       : 0.754
오래간만      : 0.751
오랜만       : 0.745

[8] sg: 1, window: 15, negative: 5
긴가민가      : 0.777
놀랐        : 0.767
기뻤        : 0.763
어땠을까      : 0.762
놀라        : 0.758

[9] sg: 1, window: 15, negative: 20
놀라        : 0.787
놀랬        : 0.778
놀랐        : 0.775
오랜만       : 0.77
어리둥절      : 0.768

CBOW ↔ Skip-Gram, window size 비교

결과 0, 1, 2와 결과 3, 4, 5를 비교하자면 아래와 같습니다.

[0] sg: 0, window: 5, negative: 10
놀란다       : 0.557
무심코       : 0.551
뭔가        : 0.55
어쩐지       : 0.546
매번        : 0.545

[1] sg: 0, window: 15, negative: 10
놀란다       : 0.642
장난        : 0.626
뭔가        : 0.621
해한다       : 0.611
정말        : 0.605

[2] sg: 0, window: 30, negative: 10
해한다       : 0.623
정말        : 0.61
멋진        : 0.608
놀랐        : 0.608
뭔가        : 0.608

[3] sg: 1, window: 5, negative: 10
놀랬        : 0.796
터뜨린다      : 0.732
어리둥절      : 0.731
열받        : 0.731
어김없이      : 0.718

[4] sg: 1, window: 15, negative: 10
놀랬        : 0.794
긴가민가      : 0.779
울컥        : 0.773
놀랐        : 0.771
오랜만       : 0.76

[5] sg: 1, window: 30, negative: 10
오랜만       : 0.819
울컥        : 0.794
그리웠       : 0.787
정말        : 0.783
은데요       : 0.777

negative 값은 10으로 통일하고, 학습 알고리즘과 window size을 변경해 실험을 진행하였습니다. CBOW로 학습한 실험 0, 1, 2이 Skip-Gram으로 학습한 실험 3, 4, 5 보다 전반적인 유사도가 비교적 낮게 나온 것을 확인할 수 있었습니다. window size에 따른 분석은 아래와 같습니다.

  • window size: 5
    • 반의어가 포함된 것을 확인할 수 있음
  • window size: 15
    • 가장 성능이 좋음
  • window size: 30
    • 관련이 없어보이는 단어들이 포함됨

number of negative samples 비교

결과 4, 6, 7, 8, 9를 비교하자면 아래와 같습니다.

[6] sg: 1, window: 15, negative: 0
문무        : 0.421
소완규       : 0.411
배닝        : 0.405
포강        : 0.403
김석휘       : 0.399

[7] sg: 1, window: 15, negative: 2
글썽이       : 0.766
울먹이       : 0.762
시큰둥       : 0.754
오래간만      : 0.751
오랜만       : 0.745

[8] sg: 1, window: 15, negative: 5
긴가민가      : 0.777
놀랐        : 0.767
기뻤        : 0.763
어땠을까      : 0.762
놀라        : 0.758

[4] sg: 1, window: 15, negative: 10
놀랬        : 0.794
긴가민가      : 0.779
울컥        : 0.773
놀랐        : 0.771
오랜만       : 0.76

[9] sg: 1, window: 15, negative: 20
놀라        : 0.787
놀랬        : 0.778
놀랐        : 0.775
오랜만       : 0.77
어리둥절      : 0.768

negative sample의 수에 따른 분석은 아래와 같습니다.

  • 0: 학습이 전혀 안됨 (절대적인 유사도 값도 낮으며, 단어들의 연관성도 없음)
  • 2: 절대적인 유사도가 눈에 띄게 높아졌으며, 유사한 단어들을 일부 포함
  • 5: 2에 비해 성능이 향상됨
  • 10: 5에 비해 성능이 향상됨
  • 20: 10에 비해 성능이 향상됨

negative sample의 수가 많을수록 아래와 같이 학습에 필요한 시간이 증가하지만, 위와 같이 성능이 점진적으로 높아짐을 확인할 수 있었습니다.

  • 0: 10min 31s
  • 2: 19min 25s
  • 5: 32min 24s
  • 10: 1h 4min 50s
  • 20: 1h 42min 2s

Reference