간단한 딥러닝 기반 장기 시계열 예측 모델 리뷰 (FiLM, NLinear)

소개

시계열 예측은 과거 시퀀스로부터 미래 시퀀스를 예측 하는 테스크로서 교통, 에너지 사용량 분석, 금융 등 다양한 분야 및 비즈니스 모델에서 활용도가 높기 때문에 큰 주목을 받아왔습니다. 시계열 예측을 정확하게 하기 위해서는 시계열 데이터에 있는 복잡한 주기성이나 경향을 포착할 수 있어야 합니다. ARIMA나 Kalman filter 같이 고전 타임시리즈 예측에 쓰이는 방법론은 주로 시계열 모델링에 대해 선형성 같은 강한 가정을 하고 있고 적절한 파라미터를 선택하는데 어려움이 있습니다. 이에 따라 데이터 내의 복잡한 모델링 능력을 배우기 위해 RNN 이나 Transformer 구조를 활용하는 딥러닝 기반의 시계열 예측 모델을 제안하는 연구가 많이 등장했습니다. 특히, 장기 시계열 예측(Long-term time series forecasting)을 효율적으로 수행하기 위해서 Informer, Autoformer, Pyraformer, FEDformer 같은 Transformer 구조의 모델이 많이 등장했습니다. 하지만, 최근 연구에서는 간단한 projection으로 장기 예측에서 이런 모델보다 높은 성능을 달성할 수 있음을 보여주고 있습니다. 이번 글에서는 간단하면서도 효과적인 딥러닝 기반 예측 모델을 소개하겠습니다.

시계열 예측 문제

출처: https://arxiv.org/pdf/2106.13008.pdf

시계열 예측은 과거 시퀀스 $(x_1, x_2, …, x_t)$가 주어졌을 때 미래 시퀀스 $(x_{t+1}, x_{t+2}, …, x_T)$를 예측하는 문제입니다. 부가적으로 과거와 미래 모든 시점에서의 정보를 가지고 있는 변수인 covariates $(c_1, c_2, …, c_T)$를 활용하는 경우도 있습니다. 예를 들어, 각 시점이 무슨 요일, 달인지 알려주는 time embedding이 covariates에 속합니다. 시계열 예측 문제는 예측하고자 하는 시리즈의 개수가 하나인 경우 univariate forecasting, 하나보다 많은 경우에는 multivarite foreacasting으로 불립니다. 또한, 출력형태가 분포인 경우 probabilistic forecasting, 각 시점마다 고정된 하나의 값을 예측하는 경우 deterministic forecasting으로 불립니다. 현재 대부분의 장기 예측 모델은 예측 값과 실제 값 사이 Mean squared error (MSE)를 줄이는 방향으로 학습하는 deterministic forecasting 모델에 해당하며 본 글에서 소개할 모델들도 모두 MSE를 기본 학습 로스로 사용합니다.

RNN, Transformer 기반 장기 예측 모델의 문제점

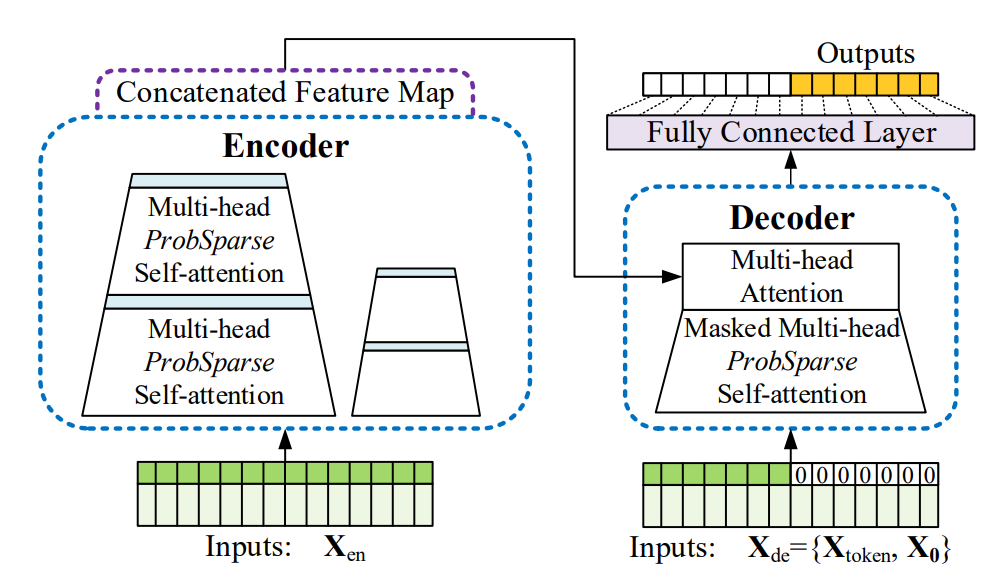
Informer 모델 구조

초기의 딥러닝 기반 예측 모델의 경우 RNN을 활용하여 autoregressive하게 예측하는 모델을 사용했습니다. AAAI’21 Best 페이퍼인 Informer는 RNN 기반 모델의 느린 추론 문제를 해결하기 위해 그림과 같은 encoder-decoder 구조에 수정된 효율적인 어텐션을 사용할 것을 제안했고 이후 transformer 기반 예측 모델이 대거 등장했습니다. 예를 들어, Autoformer는 Transformer에서 self-attention과 cross-attention 부분을 autocorrelation을 포착하는 모듈로 변경했고 FEDformer는 이 부분을 이산 푸리에 변환을 활용한 모듈로 수정해서 성능을 향상시킬 수 있었습니다. Transformer 기반 예측 모델은 점점 효율적인 attention 메커니즘을 사용하는 방향으로 발전했지만 근본적으로 이런 구조가 시계열 예측 문제에 필수적인지에 대해서는 깊게 분석하지 못 하였습니다.

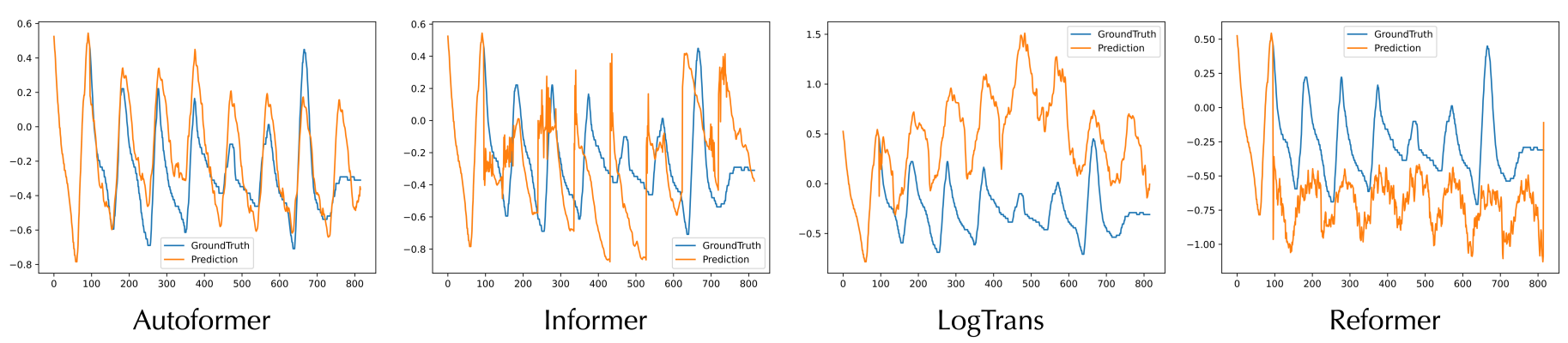
LSTM, transformer 시계열 예측 모델의 과적합 문제 (출처: https://arxiv.org/pdf/2106.13008.pdf)

최근 연구에서는 transformer 기반 예측 모델이 시계열 데이터의 노이즈에 과적합되기 쉽다는 것이 관찰되었습니다. 결과적으로 그림과 같이 LSTM, Transformer 기반 예측 모델은 새로운 입력이 들어왔을 때 실제 시리즈와 완전히 다른 형태로 시리즈를 예측하게 됩니다. 이렇게 노이즈가 심한 데이터 상에서 정확한 예측을 하기 위해서 노이즈를 제거하여 학습하는 방식을 사용하거나 강한 regularization 효과가 있는 모델을 사용할 수 있을 것입니다. 다음으로 이러한 과적합 문제를 완화하여 예측하는 모델을 제안한 두 페이퍼를 소개하겠습니다.

FiLM: Frequency improved Legendre Memory Model for Long-term Time Series Forecasting

FiLM은 이번 Neurips 2022에 어셉된 페이퍼로 시계열 예측의 과적합 문제를 완화하면서 긴 길이의 시퀀스 입력을 활용하기 위해서 다음과 같은 모델 구조를 제안합니다.

Mixture of experts 구조를 활용해서 다양한 길이의 시리즈 입력으로부터 피쳐를 추출합니다.
Legendre Memory unit을 응용해서 시계열 데이터를 표현하고 긴 과거 정보를 보존하도록 합니다.
Fourier analysis와 low-rank matrix approximation을 조합하여 시계열의 노이즈 영향을 줄입니다.

아래 그림과 같이 FiLM은 대칭적인 구조로 여러 모듈을 사용하고 있습니다. 먼저 입력을 RevIN을 통해 normalization을 하고 사용한 통계량을 써서 최종 출력을 얻을 때 다시 denormalization을 수행합니다. 서로 다른 길이의 입력에 대해 각각 LPU, FEL 모듈을 통과시켜 나온 값들을 종합하여 최종 예측을 하게 되는데 이때 사용하는 LPU 모듈 또한 입력을 분해하는 연산과 다시 합치는 연산으로 이루어져 있습니다.

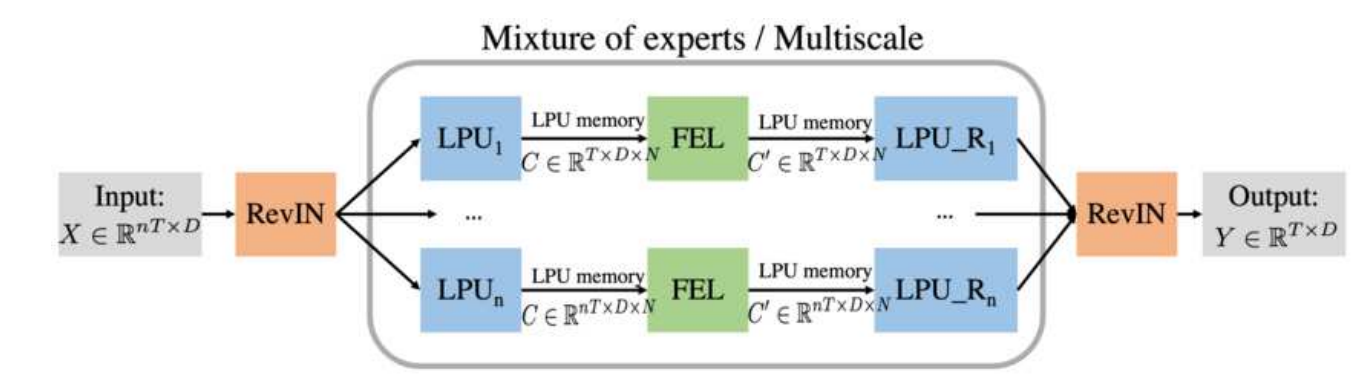
FiLM 모델 구조

Legendre Projection Unit

LPU 모듈은 과거 시퀀스를 압축하고 시간 영역의 함수의 주파수 정보를 포착하는 용도로 쓰입니다. 이런 역할을 할 수 있는 대표적은 메소드로는 FFT가 있는데 FFT는 basis로 sin, cos 같은 주기함수를 이용하는 반면 LPU는 Legendre Polynomial을 사용합니다. 좀더 구체적으로 주어진 시퀀스가 continuous하게 주어졌다고 생각하고 이를 smooth function $f(t)$로 나타내진다고 합시다. LPU는 윈도우 사이즈 $\theta$가 주어졌을 때, 각 t에 대해 $f(x)$의 윈도우 $\left[t-\theta, t\right]$ 부분 $f_{\left[t-\theta, t\right]}(x)$을 $N$개의 Legendre Polynoimial로 분해합니다. $f_{\left[t-\theta, t\right]}(x)$를 $N$개의 Legendre Polynoimial의 가중합으로 근사한 값 $g^{(t)}(x)$이 measure $µ^{(t)} =\frac{1}{\theta} \mathbb{I}\left[ t−\theta, t \right] (x)$에 대해 정의된다고 합시다.

\[g^{(t)}(x) = \sum_{n=1}^N c_n(t) P_n(\frac{2(x-t)}{\theta}+1)\]

여기서 $P_n(\cdot)$은 $n$ 번째 Legendre Polynomial을 나타냅니다. 높은 차수의 $c_n(t)$는 주어진 윈도우 시퀀스의 높은 주파수 영역 피쳐를 나타내고 낮은 차수의 $c_n(t)$은 낮은 주파수 영역 피쳐를 나타내게 됩니다. 따라서 주어진 시퀀스를 계수 $c_n$으로 나태내면 각 윈도우의 주파수 영역에서 연산을 수행할 수 있고 다시 Legendre Polynomial의 가중합을 구해서 시간 영역으로 변환할 수 있을 것입니다. 아래 그림은 랜덤 시퀀스에 LPU에 적용한 예시를 보여줍니다.

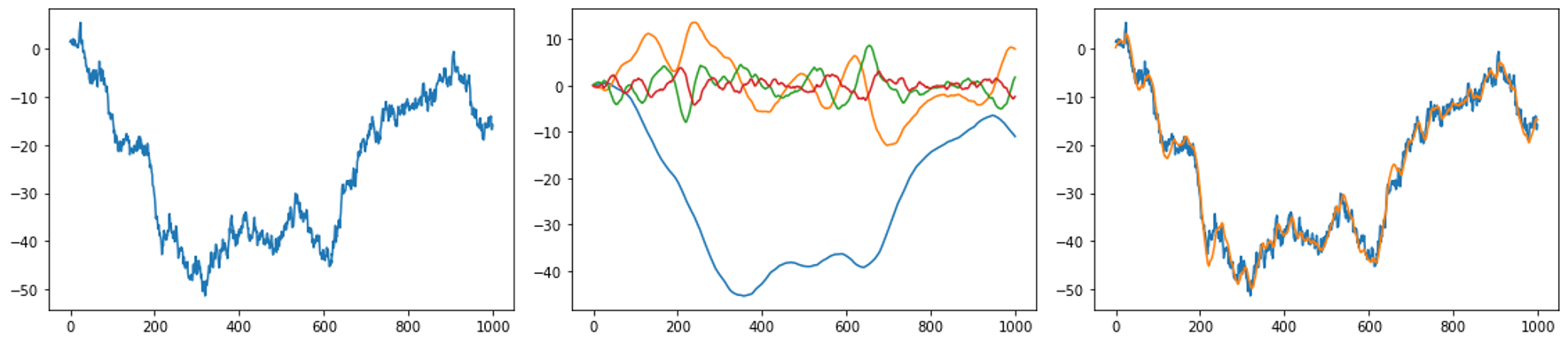
(왼쪽) Wiener process로 생성한 랜덤 시퀀스, (가운데) LPU로 분해한 결과, (오른쪽) 분해한 LPU을 다시 합친 것과 원래 시퀀스의 차이

Legendre Polynoimial로 분해를 하면 몇 가지 유용한 성질이 있습니다. 먼저, FFT로 분해를 하면 다시 원상 복구하기 위해서 대체로 많은 basis가 필요합니다. 하지만 Legendre Polynomial을 사용하면 다음과 같은 Theorem에 의해 적은 수의 basis로 압축할 수 있다는 장점이 있습니다.

If $f(x)$ is L-Lipschitz, then $\lVert f_{\left[t−θ,t\right]}(x)−g^{(t)}(x) \rVert_{\mu^{(t)}} \leq \mathcal{O}(\theta L/\sqrt N)$. Moreover, if $f(x)$ has $k$-th order bounded derivatives, we have $\lVert f_{\left[t−θ,t\right]}(x) − g^{(t)}(x)\rVert_{\mu^{(t)}} \leq \mathcal{O}(\theta^k N^{−k+1/2})$.

또한 각 $t$마다 계수 $c_n(t)$는 다음과 같은 미분 방적식을 풀어서 빠르게 구할 수 있습니다.

\[\frac{d c(t)}{dt} = -\frac{1}{\theta} A c(t) + \frac{1}{\theta} B f(t).\]

여기서 $A, B$는 고정된 메트릭스인데 자세한 내용은 위키피디아에 잘 정리가 되어 있습니다. 실제 구현에서는 이 state-space representation을 이산화하는 메서드를 이용해 계산할 수 있습니다. 아래 그림은 LPU의 계산 과정을 보여줍니다.

LPU 계산 과정

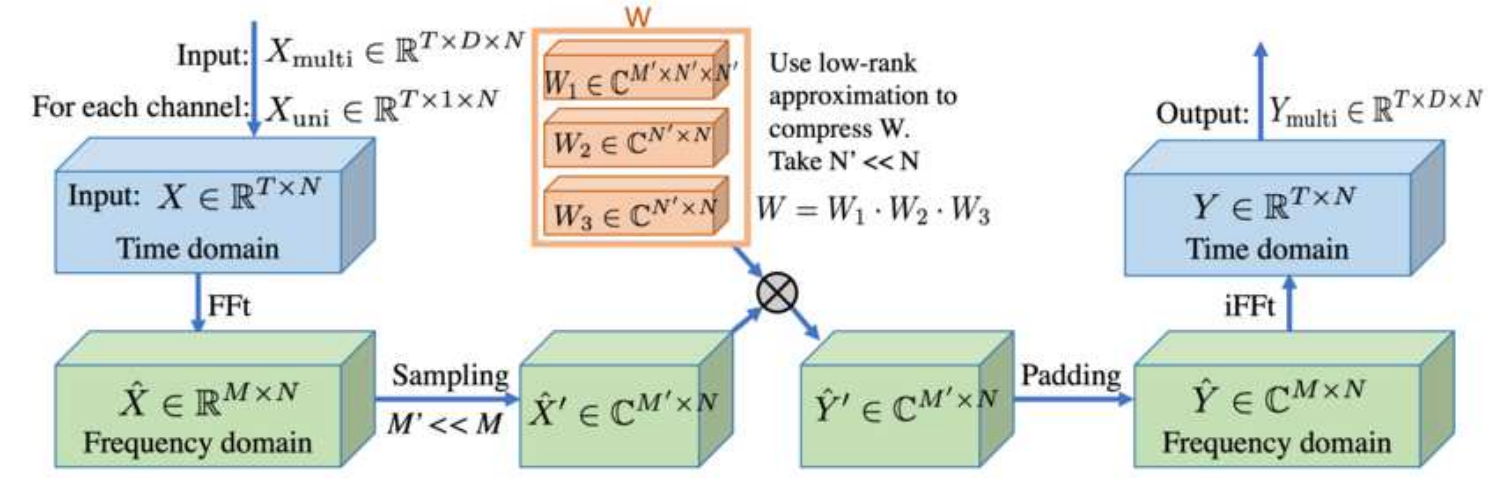
Frequency Enhanced Layer

LPU를 적용하고 나면 각 polynomial의 계수가 시퀀스 형태로 나오게 됩니다. FEL 이런 시퀀스를 다시 FFT를 이용해 일부 주파수 영역만 샘플하고 low-rank approximation을 적용해 노이즈를 제거합니다. low-rank approximation을 통해 모델 weight을 줄이고 노이즈를 제거하는 역할은 이해가 가지만 FEL에서 주파수 피쳐를 뽑기 위해 FFT를 추가로 사용하는 이유는 잘 이해가 되지 않습니다. 아마 서로 다른 basis 분해 알고리즘을 조합해서 성능이 올랐기 때문에 사용하지 않았을까 추측하고 있습니다.

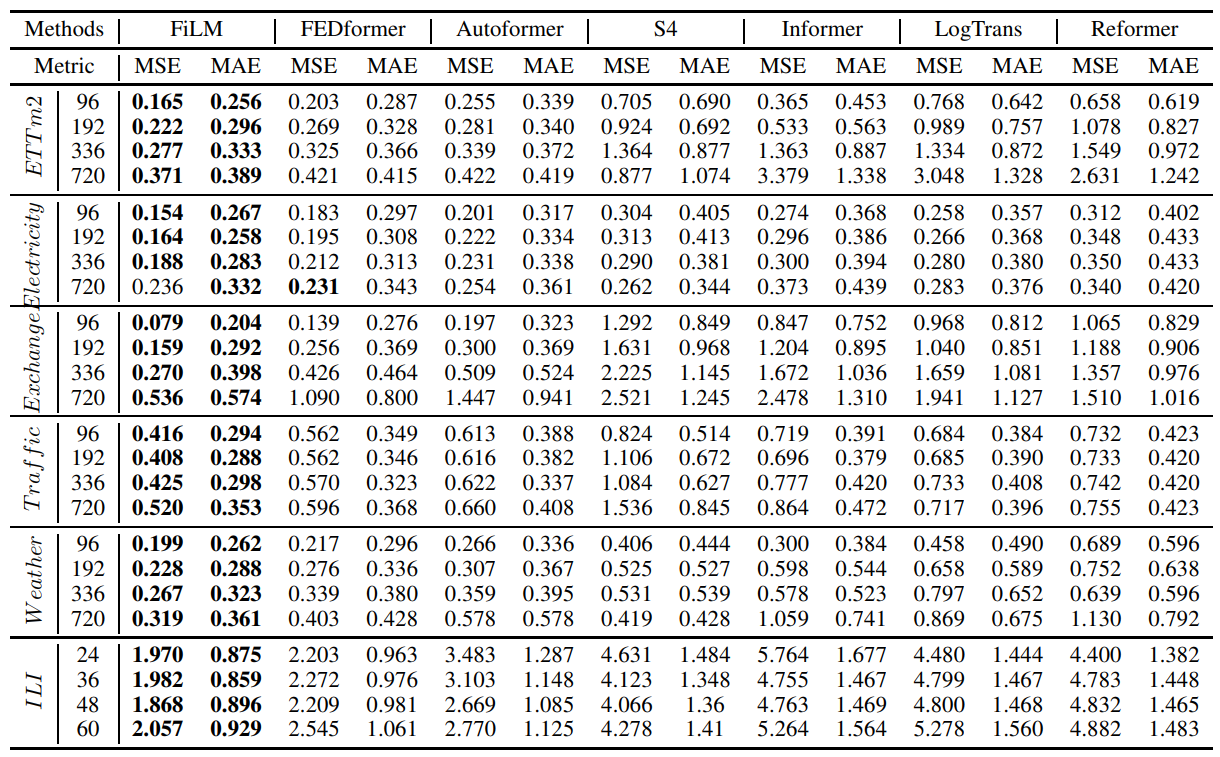
아래 성능 표와 같이 FiLM은 기존 시계열 예측 모델의 성능을 큰 폭으로 압도하는 것을 볼 수 있습니다. 기존 예측 모델에 자주 사용하고 있던 Transformer 구조가 꼭 최선이 아닐 수 있다는 점을 보여주었습니다.

Are Transformers Effective for Time Series Forecasting?

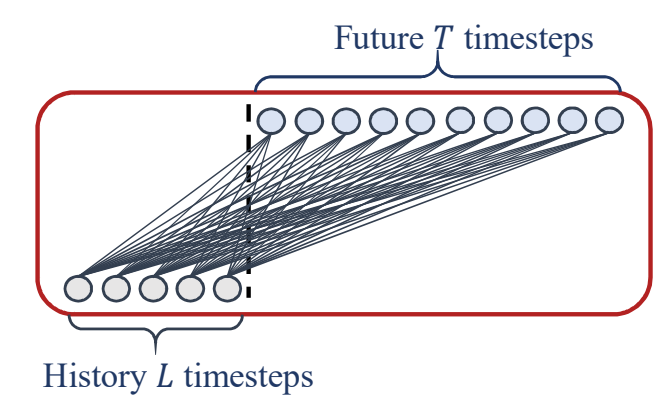
“Are Transformers Effective for Time Series Forecasting?”는 비슷한 시기에 시계열 예측에 Transformer 모델이 효과적이지 않다는 점을 보여준 페이퍼입니다. 페이퍼에서는 굉장히 간단하지만 쉽게 다른 모델을 이길 수 있는 시계열 예측 모델을 몇 가지 소개했습니다. 대표적으로 NLinear라고 불리는 모델은 아래 그림과 같은 리니어 모델을 사용하는데 여기서 입력 시퀀스에서 마지막 입력 $x_t$를 뺀 벡터를 입력으로 넣어주고 출력 시퀀스에서 다시 이 값을 더해서 예측을 합니다. 또한 Multivariate forecasting에서는 모든 시리즈에 이 리니어 모듈의 가중치를 공유해서 사용합니다.

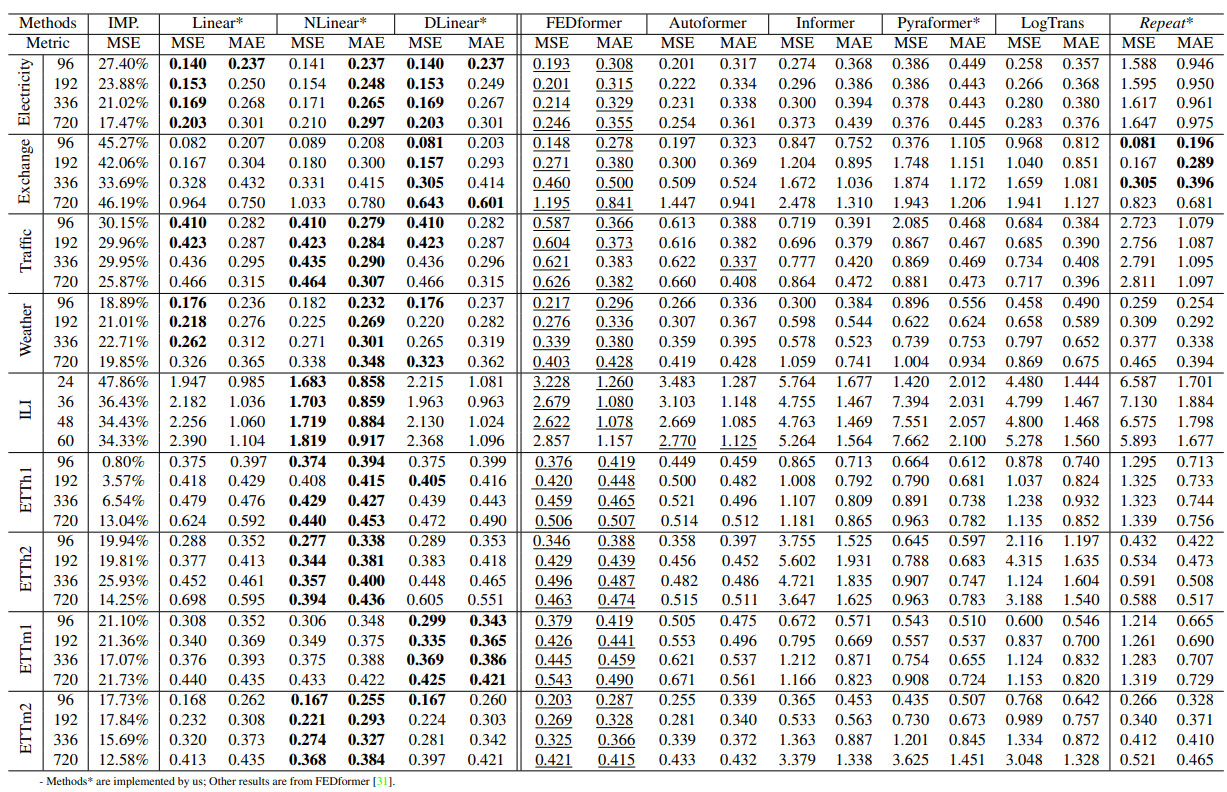
놀랍게도 이런 모델은 기존 Transformer 기반 모델의 성능을 쉽게 압도할 수 있었습니다. 이외에도 입력 시퀀스의 마지막 값을 단순 복사해서 예측하는 모델(Repeat)이 Exchange 같은 노이즈가 많은 데이터 셋에서 성능이 꽤 높다는 점을 보여주기도 했습니다.

마치며

이번 글에서는 시계열 데이터에서 잘 작동하고 있는 Projection 기반 예측 모델 몇 가지에 대해서 소개해보았습니다. 다른 딥러닝 테스크와 다르게 시계열 데이터에서는 단순한 모델이 쉽게 복잡한 모델의 성능을 뛰어 넘는 것을 보아 단순히 복잡도를 키우는 방식이 효과적일지 고민해보아야 할 것 같습니다. 시계열 데이터는 대체로 노이즈가 심하고 시간의 흐름에 따라 경향이 바뀌는 경우가 흔합니다(Non-stationary data). 과적합의 위험에서 벗어나 이러한 데이터로 딥러닝 모델을 학습하는 것은 여전히 어려운 일입니다. 시계열 예측 연구에서는 시계열 데이터의 특성을 고려해서 과적합이 덜 일어나게 학습하는 방법론을 찾는 것이 중요해질 것으로 보입니다.