Kirchhoff's Theorem (Matrix-Tree Theorem)
이번 글에서는 그래프의 스패닝 트리의 개수를 세는 두 가지 정리, Cayley’s formula와 Kirchhoff’s theorem에 대해 소개합니다.
Cayley’s Formula
일반 그래프의 스패닝 트리의 개수를 세어보기에 앞서, 특수한 경우부터 먼저 살펴봅시다.
Theorem 1 (Cayley’s Formula). $n$개의 정점으로 이루어진 완전그래프 $K_n$의 스패닝 트리의 개수는 $n^{n-2}$이다.
이 정리를 증명하는 방법으로는 여러 가지가 알려져 있으며, 대표적으로 Prüfer sequence와의 일대일 대응 관계를 찾는 증명이 있습니다. 개인적으로 가장 마음에 드는 증명은 다음과 같은 더블 카운팅을 이용한 증명입니다. 책 “하늘책의 증명” (Proofs from THE BOOK)에도 실린 증명이라고 합니다.
Proof. $n$개의 정점으로 이루어진 완전그래프의 스패닝 트리의 개수를 $T_n$이라고 합시다.
이제 두 가지 방법으로, “방향 있는 간선을 하나씩 추가해서 루트가 있는 스패닝 트리를 만드는 방법”의 수를 세어 보겠습니다. 이때 간선의 방향은 루트에서 멀어지는 방향이어야 합니다.
첫 번째 방법은 스패닝 트리에서 아무 정점 하나를 루트로 잡고, 각 간선에 순서를 부여하는 방법입니다. 루트로 잡을 수 있는 정점은 $n$개, 간선의 순서로 가능한 순열은 $(n-1)!$가지이므로 총 $T_n n!$가지 방법이 존재합니다.
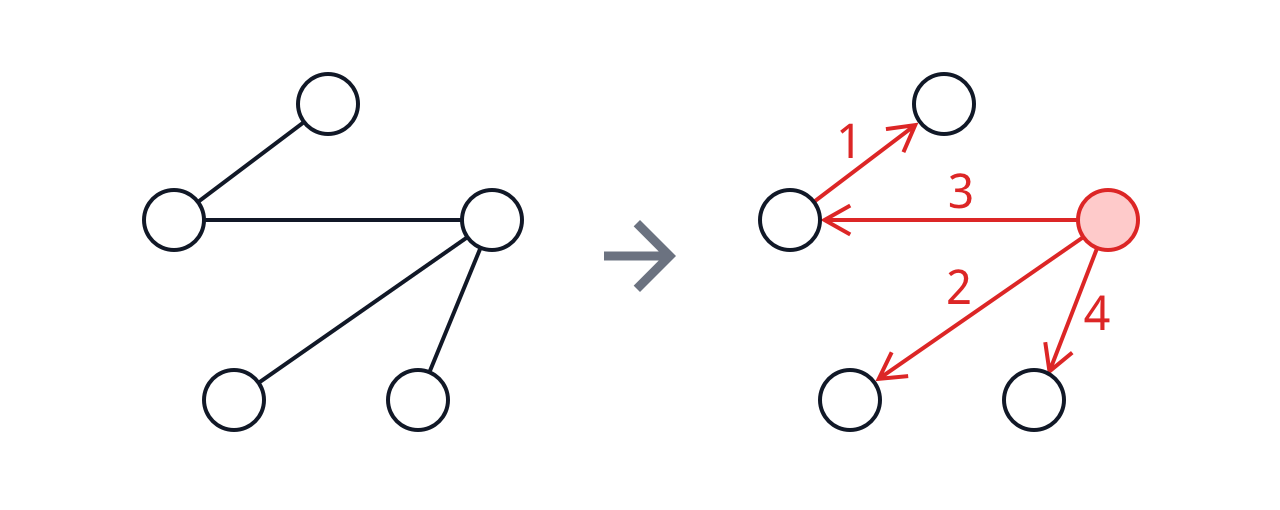
두 번째 방법은 직접 간선을 하나씩 추가해 나가는 방법입니다. 지금까지 $n-k$개의 간선을 추가했다면 $k$개의 트리로 구성된 forest가 만들어집니다. 다음에 추가할 간선의 시작점은 아무 정점이나 가능하고, 끝점은 시작점이 속하지 않은 어떤 트리의 루트여야 합니다. 따라서, 시작점으로 고를 수 있는 정점의 수는 $n$개, 끝점으로 고를 수 있는 정점의 수는 $k-1$개입니다. 모든 $2\le k\le n$에 대해서 $n(k-1)$을 곱하면 $n^{n-1}(n-1)! = n^{n-2}n!$가지 방법이 나옵니다.
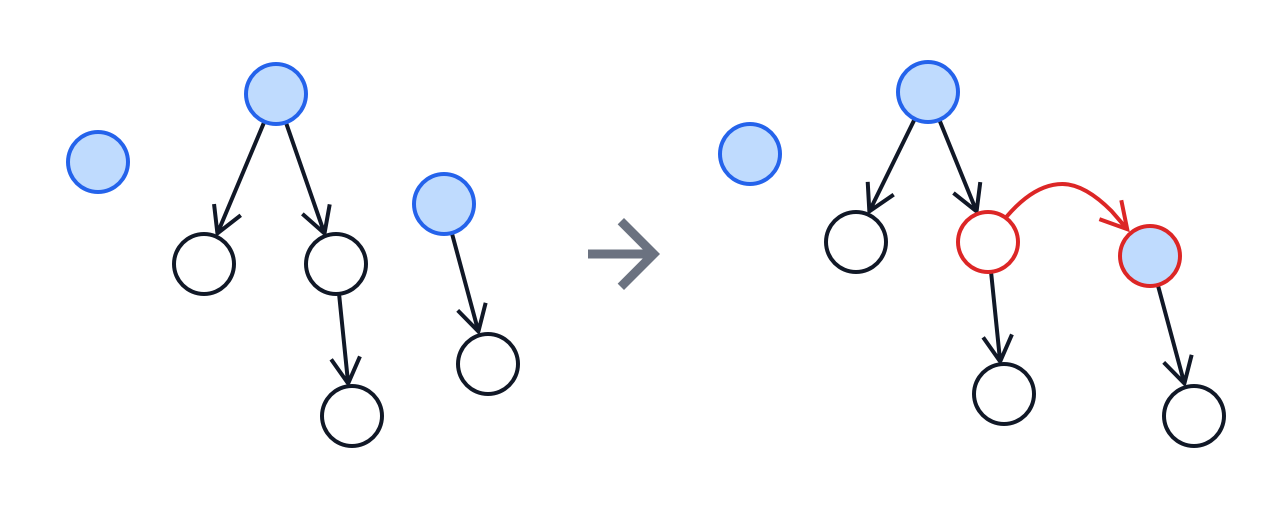
따라서, $T_n n! = n^{n-2}n!$에서 $T_n = n^{n-2}$를 얻을 수 있습니다. $\square$
Laplacian Matrix
완전그래프의 스패닝 트리의 개수를 세어봤으니, 이제 임의의 그래프로 확장할 차례입니다. Kirchhoff’s theorem은 임의의 그래프에서 스패닝 트리의 개수를 세는 정리입니다. 정리를 소개하기에 앞서, 먼저 Laplacian matrix라는 개념을 알아야 합니다.
Definition (Laplacian Matrix). $n$개의 정점 $v_1, \cdots, v_n$을 가지는 그래프 $G$가 있을 때, 이 그래프의 Laplacian Matrix $L_G$는 다음과 같이 정의되는 $n \times n$ 행렬이다.
\[(L_G)_{i,j} = D - A\]여기서 $D$는 그래프의 차수 행렬 (degree matrix), $A$는 그래프의 인접 행렬 (adjacency matrix)이며, 각각 다음과 같이 정의된다.
\[(D)_{i,j} = \begin{cases}\deg(v_i) & \text{if $i=j$} \\ 0 & \text{otherwise} \end{cases}\] \[(A)_{i,j} = \begin{cases} 1 & \text{if $v_i$ and $v_j$ are adjacent} \\ 0 & \text{otherwise} \end{cases}\]예를 들어, 다음과 같은 그래프가 있다고 합시다.
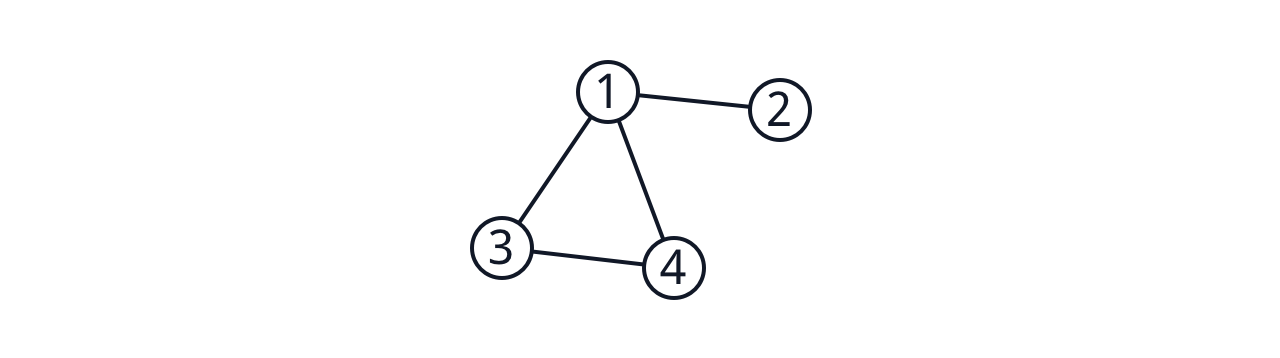
이 그래프의 Laplacian matrix는 다음과 같습니다.
\[L_G = \begin{bmatrix}3&0&0&0 \\ 0&1&0&0 \\ 0&0&2&0 \\ 0&0&0&2\end{bmatrix} - \begin{bmatrix}0&1&1&1 \\ 1&0&0&0 \\ 1&0&0&1 \\ 1&0&1&0\end{bmatrix} = \begin{bmatrix}3&-1&-1&-1 \\ -1&1&0&0 \\ -1&0&2&-1 \\ -1&0&-1&2\end{bmatrix}\]Laplacian matrix는 근접 행렬 (incidence matrix)를 이용해서 계산할 수도 있습니다. 그래프 $G$의 정점의 개수가 $n$, 간선의 개수가 $m$일 때, incidence matrix는 다음과 같은 $n\times m$ 행렬로 정의됩니다.
\[(B)_{v,e} = \begin{cases} -1 & \text{if $v=v_i$} \\ 1 & \text{if $v=v_j$} \\ 0 & \text{otherwise} \end{cases} \quad\text{where $e=(v_i, v_j)$ and $i<j$}\]이때, Laplacian matrix는 $L_G = BB^T$를 만족합니다.
마지막으로, Laplacian matrix의 행렬식은 항상 0입니다. Laplacian matrix의 모든 열의 합이 0이므로, 열끼리 선형 독립이 아니기 때문입니다.
Kirchhoff’s Theorem
이제 본격적으로 Kirchhoff’s theorem에 대해 알아봅시다.
Theorem (Kirchhoff’s Theorem). 행렬 $A$에서 $i$행과 $i$열을 제거한 것을 $A[i]$로 나타내자. 그래프 $G$의 스패닝 트리의 개수를 $\tau(G)$라고 할 때, 임의의 $i$에 대해 다음이 성립한다.
\[\tau(G) = \det(L_G[i])\]이 정리는 행렬을 통해 스패닝 트리의 개수를 센다는 점에서 비롯해 matrix-tree theorem이라고 부르기도 합니다. Kirchhoff’s theorem의 증명은 크게 두 가지가 알려져 있는데, 하나는 선형대수학의 정리인 Cauchy-Binet formula를 사용하는 방법이고, 다른 하나는 수학적 귀납법을 이용한 기초적인 증명 (elementary proof)입니다. 이 글에서는 후자만을 소개합니다.
증명에 앞서 간단한 사실 하나를 짚고 넘어가겠습니다. $E_{ii}$를 $(i, i)$ 위치의 원소만 1이고 나머지 원소는 0인 행렬로 정의합시다. 임의의 행렬 $A$에 대해 다음이 성립합니다.
\[\det(A+E_{ii}) = \det(A) + \det(A[i])\]이 사실은 순열을 통해 행렬식을 계산하는 식을 떠올리면 쉽게 확인할 수 있습니다. $A_{i,i}$를 1 증가시킬 때 더해지는 값은 $(i,i)$를 지나는 순열에 대한 alternating sum과 같고, 이는 곧 $\det(A[i])$입니다.
이제 Kirchhoff’s theorem을 증명해 봅시다.
Proof. 그래프의 정점 및 간선의 개수에 대한 수학적 귀납법을 사용합니다.
Base case: 그래프가 정점 두 개와 간선 0개로 이루어져 있다면,
\[L_G = \begin{bmatrix}0&0\\0&0 \end{bmatrix}\]입니다. $\det(L_G[1]) = \det(L_G[2]) = \tau(G) = 0$이므로 정리를 만족합니다.
Inductive step: 먼저 정점 $i$에 인접한 간선이 없는 경우부터 처리합시다. 이 경우에는 $\det(L_G[i]) = \det(L_{G-i}) = 0$입니다. 스패닝 트리가 존재하지 않는 경우이므로 정리를 만족합니다.
이제 정점 $i$에 대해서, 이 정점에 인접한 간선 $e = (i, j)$를 생각해 봅시다. 스패닝 트리를 구성할 때 이 간선을 포함하거나 제외할 수 있습니다. 두 가지 경우의 수를 합치면 전체 스패닝 트리의 개수가 나옵니다.
각 경우를 표현하기 위해, 그래프에서 간선의 deletion과 contraction이라는 개념을 정의합시다.
- Deletion: 그래프에서 간선 $e$를 제거한 그래프를 나타내며, $G - e$와 같이 표기합니다.
- Contraction: 그래프에서 간선 $e$의 양 끝 정점을 하나로 합친 그래프를 나타내며, $G / e$와 같이 표기합니다.
그러면 간선 $e$를 제외하고 스패닝 트리를 구성하는 경우의 수는 $\tau(G-e)$, 간선 $e$를 포함하여 스패닝 트리를 구성하는 경우의 수는 $\tau(G/e)$와 같습니다. 즉,
\[\tau(G) = \tau(G-e) + \tau(G/e)\]가 성립합니다.
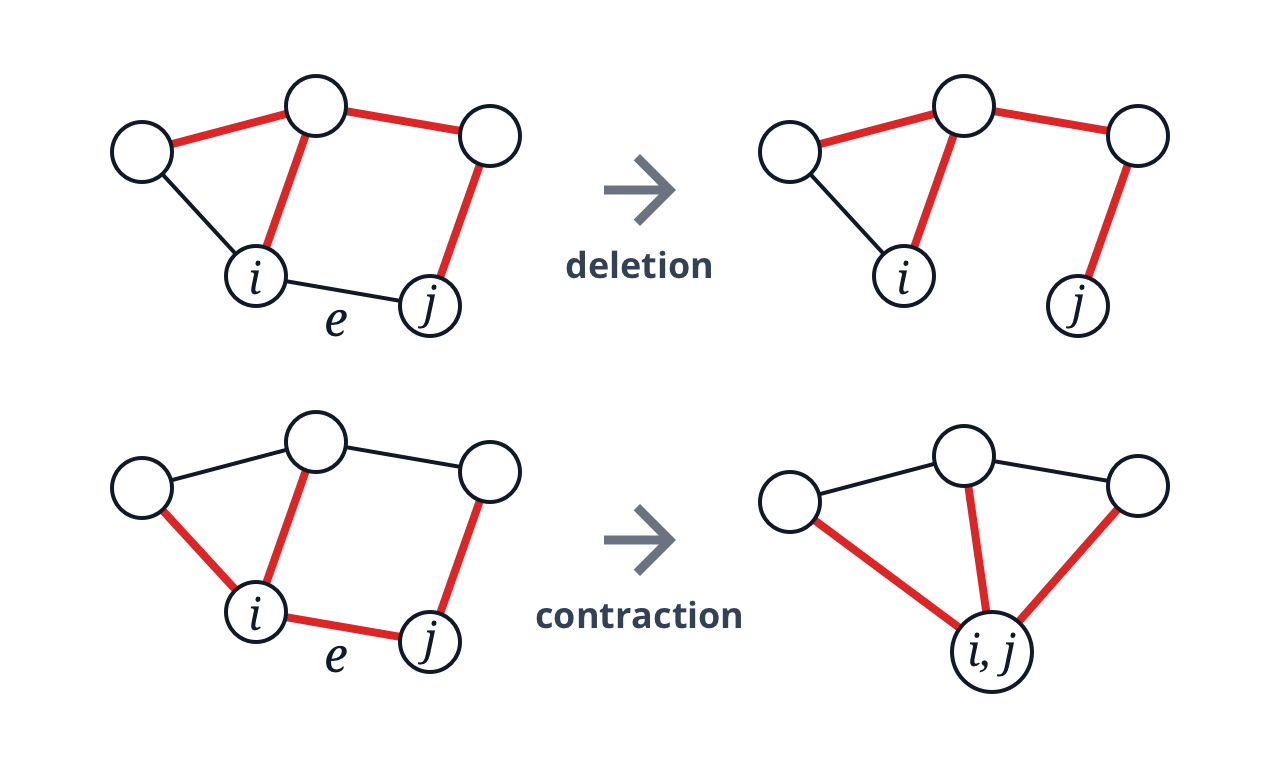
귀납 가설에 따라, 간선 또는 정점의 수가 더 적은 그래프인 $G-e$와 $G/e$에서는 정리가 성립합니다. 따라서 우리는 다음과 같은 사실을 증명하면 됩니다.
\[\det(L_G[i]) = \det(L_{G-e}[i]) + \det(L_{G/e}[i])\]먼저 deletion을 한 경우부터 살펴봅시다. 어차피 Laplacian matrix의 $i$행과 $i$열은 무시하므로, 행렬에 영향을 미치는 것은 $j$의 차수가 1 감소한다는 사실 뿐입니다. 즉, $L_G[i] = L_{G-e}[i] + E_{jj}$입니다. 따라서
\[\begin{align*} \det(L_G[i]) &= \det(L_{G-e}[i] + E_{jj}) \\ &= \det(L_{G-e}[i]) + \det(L_{G-e}[i,j]) \\ &= \det(L_{G-e}[i]) + \det(L_G[i,j]) \end{align*}\]가 성립합니다. 여기서 $L_G[i,j]$는 행렬의 $i$행과 열, $j$행과 열을 모두 제거한 행렬을 나타냅니다. $L_G$와 $L_{G-e}$의 차이는 $i$, $j$번째 행과 열 뿐이므로, $L_{G-e}[i,j] = L_G[i,j]$이고 마지막 등호가 성립합니다.
이번에는 contraction을 한 경우를 살펴봅시다. 정점 $i$를 정점 $j$쪽으로 합쳤다고 생각하면, $L_G$에서 $i$행과 열을 제거하고 $i$행/열의 정보를 $j$행/열에 업데이트한 것으로 생각할 수 있습니다. $L_G[i]$와 $L_{G/e}$의 차이는 $j$번째 행과 열 뿐이므로, $L_{G/e}[j] = L_G[i,j]$가 성립합니다.
이 사실을 위의 등식에 대입하면 다음이 성립합니다.
\[\begin{align*} \det(L_G[i]) &= \det(L_{G-e}[i]) + \det(L_{G/e}[j]) \\ &= \tau(G-e) + \tau(G/e) = \tau(G) \end{align*}\]수학적 귀납법에 의해, Kirchhoff’s theorem은 모든 그래프에서 성립합니다. $\square$
기타 사실들
글에서 언급하지 않은 사실들을 몇 가지 더 나열하자면 다음과 같습니다.
-
다변수 미적분학을 배운 적 있는 독자라면 Laplacian matrix라는 이름이 어딘가 익숙할 겁니다. 실제로 이 행렬이 Laplacian matrix라고 불리는 이유는 다변수 미적분학에서 등장하는 Laplacian 연산자($\Delta$)와 비슷한 기능을 하기 때문입니다. $n\times n$ Laplacian matrix는 $n$차원 벡터에 대한 변환으로 생각할 수 있는데, 이 $n$차원 벡터를 “각 정점을 어떤 수에 대응시키는 함수”라고 생각하면 Laplace 연산자와 비교가 가능해집니다.
- 다변수 함수 $f$에 대해, $\Delta f(p)$는 어떤 점 $p$에서의 함숫값 $f(p)$가 $p$ 주변의 함숫값의 평균보다 얼마나 작은지를 나타냅니다.
- $n$차원 벡터 $f$에 대해 $(L_G f)_i$는 정점 $i$에서의 벡터값 $f_i$가 정점 $i$에 인접한 정점들의 벡터값보다 얼마나 큰지를 나타냅니다.
구하는 값의 부호가 서로 다르긴 하지만, 두 개념이 대강 비슷한 역할을 한다는 사실을 알 수 있습니다. Laplacian이 gradient의 divergent로 정의된다는 사실 ($\Delta f = \nabla \cdot \nabla f$) 역시 위에서 소개한 식 $L_G = BB^T$에 대응되므로 직접 비교해 보시기 바랍니다.
- 증명에서 등장한 $\tau(G) = \tau(G-e) + \tau(G/e)$와 같은 형태의 식을 deletion-contraction formula라고 하며, 그래프 이론에서 종종 등장하는 형태의 재귀식입니다. 이를 만족하는 다른 예시로는 채색다항식 (chromatic polynomial)이 있습니다.
- 사실, 스패닝 트리의 개수는 $L_G$의 임의의 cofactor와 동일합니다. 즉, $i$행 $i$열을 지운 행렬 뿐만 아니라 $i$행 $j$열을 지운 행렬의 determinant를 구하고 $(-1)^{i+j}$를 곱해서 스패닝 트리의 개수를 구할 수도 있습니다.
참고 자료
- Cayley’s formula
- Laplacian matrix
- Kirchhoff’s theorem
- Deletion-contraction formula