Mining Multi-Label Samples from Single Positive Labels (NeurIPS'22) 눈문 소개

machine-learning

올해 11월 말에 열릴 머신러닝 학회인 NeurIPS 2022에 제가 제출했던 논문 “Mining Multi-Label Samples from Single Positive Labels”이 어셉되어서 리뷰하고자 합니다.

소개

자연에 존재하는 많은 이미지 데이터셋은 여러 가지의 속성을 가지고 있습니다. 예를 들어, 얼굴 이미지 데이터셋은 검은 머리, 웃는 표정, 남성과 같은 속성을 가질 수 있습니다. 일반적으로 이런 다중 속성을 모두 조작하여 이미지를 생성하기 위해서는 모든 속성의 존재 여부가 레이블링된(다중 레이블) 데이터셋을 사용해야 하는데 이는 대채로 매우 비쌉니다. “Mining Multi-Label Samples from Single Positive Labels”은 하나의 속성만 존재함을 알 수 있는 이미지로 이루어진 데이터셋을 이용해서 여러가지 속성이 존재 및 부재한 이미지를 샘플링 알고리즘으로 생성하는 방법을 제시합니다.

아래 그림처럼 두 클래스가 주어졌을 때 논문이 제안한 샘플링 프레임워크(S2M sampling)를 사용하면 두 클래스 모두에 속하는 데이터와 한 클래스에는 포함하지만 나머지 클래스에서는 포함되지 않는 데이터를 생성할 수 있습니다.

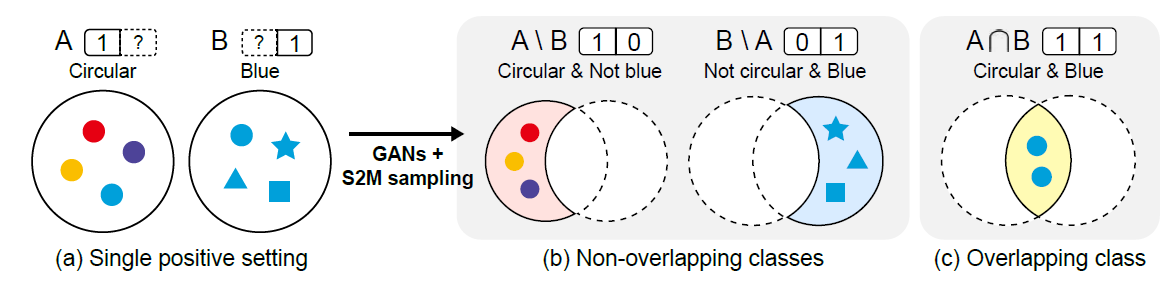
제안된 S2M sampling을 사용했을 때 나올 수 있는 결과물

단일 양성 레이블과 다중 레이블 데이터

하나의 속성만 존재함을 나타내는 레이블을 단일 양성 레이블(single positive label)이라고 부릅니다. 앞에서 얘기한 얼굴 이미지 데이터 셋을 예로 들면, 검은 머리 이미지 데이터 셋, 웃는 표정의 이미지 데이터 셋, 남성 이미지 데이터 셋 각각은 하나의 속성이 존재함만을 알 수 있습니다. 이 세 데이터 셋을 이용해 검은 머리의 웃는 남성 이미지, 검은 머리의 웃지 않는 여성 이미지 등을 생성하는 것이 목표입니다. 이러한 방식은 단일 양성 레이블이 다중 레이블 데이터 비해서 쉽게 모을 수 있기 때문에 적은 비용으로 다중 속성 이미지를 생성할 수 있다는 장점이 있습니다.

구체적으로 이미지 $X$가 $i$번째 속성이 존재하는 경우 $y_i=1$ 부재한 경우 $y_i=0$이라고 나타냅시다. $j$번 속성의 존재를 아는 단일 양성 레이블 데이터는 클래스 조건부 분포 $p(x\vert y_j=1)$에서 샘플되었다고 생각할 수 있습니다. $I$와 $J$를 각각 존재하는 속성의 인덱스 집합과 부재하는 인덱스 집합이라고 나타내면 다중 레이블 데이터는 $p_{(I,J)}(x):= p(x\vert \forall i\in I, \forall j\in J, y_i=1,y_j=0)$에서 샘플되었다고 볼 수 있습니다. 만약 임의의 두 다른 인덱스 $i$, $j$에 대해 supp $p(x\vert y_i=1, y_j=0)$와 supp $p(x\vert y_j=1, y_i=0)$이 겹치지 않는다고 가정하면 다음과 같은 식이 성립합니다.

\[p_{(I,J)}(x) = \pi_{(I,J)}^{-1}\left(\min\{\pi_i p(x|y_i=1): i\in I\} - \max\{\pi_j p(x|y_j=1): j\in J\} \cup \{0\}\right)^+\]

여기서 $\pi_{(I,J)}:=p(\forall i\in I, \forall j\in J, y_i=1,y_j=0), \pi_i:=p(y_i=1)$ 입니다. 자세한 증명은 논문의 부록에 있습니다. 간략하게 아이디어를 설명하면 먼저 $J=\emptyset$ 인 경우에 위 식이 성립함을 보이고 포함과 배제의 원리에 따라 일반적인 경우까지 보일 수 있습니다. 아래 그림은 문제 세팅을 요약합니다.

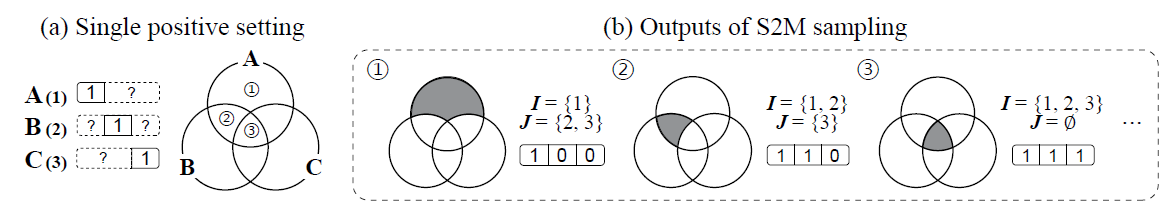
단일 양성 레이블이 주어졌을 때 다중 레이블을 생성하는 문제

다중 레이블 데이터 생성

앞 절에서 다중 레이블 데이터 분포와 단일 양성 레이블 분포간 관계를 이끌어 냈습니다. 하지만, 이 관계 식은 많은 변수와 $p(x\vert y_i=1)$와 같이 암시적으로 정의된 밀도 식으로 이루어져 있기 때문에 해당 분포의 생성 모델을 바로 학습하기는 쉽지 않아 보입니다. 기존 연구에서 GANs를 활용하여 복잡한 생성 분포를 학습하고 샘플링 알고리즘을 적용하여 원하는 타겟 분포에 가깝게 샘플을 얻을 수 있는 방법이 제시된바가 있습니다(DRS 소개글 참고). 우리는 이러한 방법을 응용하여 $p_{(I,J)}$의 서포트를 포함하는 분포의 생성 네트워크를 학습하고 여러가지 분류기를 학습하여 샘플링 알고리즘을 적용하는 트릭을 사용할 것입니다.

여기에 적용할 수 있는 샘플링 알고리즘은 여러가지가 있는데 논문에서는 주로 independent metropolis-hastings (IMH) 알고리즘을 적용하는 방법에 대해서 소개합니다. IMH 알고리즘은 현재 상태와 독립적인 proposal 분포 $q$가 있을 때 타겟 분포 $p_{tg}$에서 근사적으로 샘플을 얻게 하는 간단한 알고리즘으로, 현재 상태 $x_t$에서 accept-reject step을 통해 다음 스탭의 상태 $x_{t+1}$를 결정하는 Markov process를 사용합니다. accept-reject step을 수행하기 위해서 매 스탭 $t$마다 $q$로부터 샘플 $x’$을 얻고 다음과 같이 정의되는 acceptance probability $\alpha(x’, x_t)$를 계산합니다.

\[\alpha (x', x_t)=\min\left(1, \frac{p_{tg}(x')q(x_t)}{p_{tg}(x_t)q(x')}\right)\]

그리고 나서 다음 스탭의 상태 $x_{t+1}$의 값을 $\alpha(x’, x_t)$의 확률로 $x_{t+1}=x’$로 놓고 $1-\alpha(x’, x_t)$의 확률로 $x_{t+1}=x_t$로 놓게 됩니다. Ergodicity와 관련된 몇가지 가벼운 조건(예를 들어, $p_{tg}/q$이 uniformly bounded 하다거나)을 만족하는 경우 이 accept-reject step을 반복하면 스탭 $t$가 증가할수록 $x_t$의 분포가 $p_{tg}$로 수렴함이 증명되어 있습니다.

생성 네트워크 $G$가 주어져 있고 생성 분포 $p_G$의 서포트가 $p_{(I,J)}$의 서포트를 포함하고 있다고 가정합시다. 단순하게는 주어진 모든 데이터를 가지고 GANs, VAE 같은 생성 네트워크를 학습하는 방식으로 이러한 $G$를 얻을 수 있을 것입니다. IMH 샘플링 알고리즘을 적용하기 위해 $p_{tg}=p_{(I,J)}$, $q=p_G$로 둡니다. 그러면

\[\alpha(x', x_t)=\min\left(1, \frac{p_{tg}(x')q(x_t)}{p_{tg}(x_t)q(x')}\right) =\min\left(1, \frac{p_{(I, J)}(x')p_G(x_t)}{p_{(I,J)}(x_t)p_G(x')}\right)\]

가 됩니다. 자세히 보면 이 식은 $p_G$와 $p_{(I,J)}$ 사이 비율인 $p_{(I,J)}/p_G$를 알고 있으면 계산할 수 있습니다. 결과적으로는 모든 $x$에 대해 이 확률 밀도 비율을 계산할 수 있으면 근사적으로 $p_{(I,J)}$에서 샘플을 얻을 수 있습니다.

확률 밀도 비율 계산하기

보통 주어진 데이터의 분포와 이를 가지고 학습한 생성 모델의 샘플 분포에는 차이가 있고 생성하고자 하는 샘플의 class prior가 데이터 셋 상의 class prior와 다를 수 있기 때문에 $p_{data}$라는 데이터의 확률 밀도 함수를 새로 도입하겠습니다. 즉, $p_{data}(x\vert y_i=1) = p(x\vert y_i=1)$을 만족하지만 $p_{data}(y_i=1)$ 과 $p(y_i=1)$, $p_{data}(x)$ 과 $p_G(x)$는 각각 다를 수 있습니다.

확률 밀도 비율을 구하기 위해서 여러가지 분류기 ($D_v, D_r, D_f$)를 아래와 같은 로스를 가지고 학습할 것입니다. 분류기 $D_v$는 실제 데이터와 생성된 샘플 사이를 분류하고 $D_r$과 $D_f$는 각각 실제 데이터와 생성된 샘플의 클래스를 분류합니다.

\[\mathcal{L}_v = -\mathbb{E}_{(x,c)\sim p_{data}(x,c)}[\log D_v(x)] - \mathbb{E}_{x\sim p_G(x)}[\log (1- D_v(x))]\] \[\mathcal{L}_r = -\mathbb{E}_{(x,c)\sim p_{data}(x,c)}[\log D_r(c|x)]\] \[\mathcal{L}_f = -\mathbb{E}_{(x,c)\sim p_G(x,c)}[\log D_f(c|x)]\]

이 로스를 줄여서 얻은 최적의 분류기 $D_v^\ast, D_r^\ast, D_f^\ast$는 다음을 만족합니다.

\[D_v^\ast(x) = \frac{p_{data}(x)}{p_{data}(x) + p_G(x)}, D_r^\ast(c\vert x) = \frac{p(x\vert y_c=1) p_{data}(c)}{p_{data}(x)}, D_f^\ast(c\vert x) = \frac{p_G(x\vert c) p_G(c)}{p_G(x)}\]

그러면 $D_v^\ast, D_r^\ast, D_f^\ast$로부터 각각 $\frac{p_{data}(x)}{p_G(x)}$, $\frac{p(x\vert y_c=1)}{p_{data}(x)}$, $\frac{p_G(x\vert c)}{p_G(x)}$을 계산할 수 있습니다. 분류기 $D_v^\ast, D_r^\ast$의 출력값과 처음에 구했던 $p_{(I,J)}$의 다른 표현을 사용하면 아래와 같이 샘플링 알고리즘에 필요한 acceptance probability를 계산할 수 있습니다.

\[r_{(I, J)}(x) := \left(\min\left\{\frac{\pi_i}{p_{data}(i)}D_r^\ast(i\vert x): i\in I\right\} \right.\left.- \max\left\{\frac{\pi_j}{p_{data}(j)}D_r^\ast(j\vert x):j\in J\right\}\cup\left\{0\right\} \right)^+,\\ \alpha(x', x) = \min\left(1, \frac{p_{(I,J)}(x')/p_G(x')}{p_{(I,J)}(x)/p_G(x)}\right) = \min\left(1,\frac{r_{(I,J)}(x')({D_v^\ast(x)}^{-1}-1)}{r_{(I,J)}(x)({D_v^\ast(x')}^{-1}-1)}\right)\]

샘플링 알고리즘에서 클래스 조건부 생성모델 $p_G(x\vert c)$을 proposal로 사용하는 경우에 $p_{(I,J)}$에 더 가깝기 때문에 샘플링 효율이 더 좋아집니다. 이때는 $D_f^\ast$를 추가로 사용하여 다음과 같이 적절한 acceptance probability를 계산할 수 있습니다.

\[\alpha_c(x', x) = \min\left(1, \frac{p_{(I,J)}(x')/p_G(x'\vert c)}{p_{(I,J)}(x)/p_G(x\vert c)}\right) = \min\left(1,\frac{r_{(I,J)}(x')D_f^\ast(c\vert x)({D_v^\ast(x)}^{-1}-1)}{r_{(I,J)}(x)D_f^\ast(c\vert x')({D_v^\ast(x')}^{-1}-1)}\right)\]

잠재 변수 피팅을 통해 샘플링 효율 높이기

만약 proposal 분포와 타겟 분포가 크게 다르면 샘플링 알고리즘의 수렴속도가 매우 느려집니다. 특히, IMH 알고리즘이 수렴하는데 걸리는 시간은 생성 샘플 중 타겟 클래스에 속하는 샘플 비율에 반비례하기 때문에 속성 수가 증가할수록 샘플링 속도가 기하급수적으로 느려집니다. 이러한 문제를 해결하기 위해서 타겟 클래스의 샘플을 찾았을 때 이를 이용하여 지속적으로 proposal을 타겟 분포에 가깝게 업데이트해주는 트릭을 사용합니다.

논문에서는 주로 가우시안같은 간단한 잠재 변수 $z$로부터 이미지 $x$의 맵핑 $G$를 배우는 GANs를 생성 모델로 사용하는 경우를 다뤘습니다. 초기 샘플링을 통해 얻은 타겟 클래스의 샘플 $x_{1: m}$을 얻은 뒤 이에 대응하는($G(z_i) =x_i$를 만족하는) 잠재 샘플 $z_{1: m}$을 구합니다. 이 잠재 샘플들을 가지고 새로운 잠재 분포 $\tilde{p}_z$를 구하고 $G$에 의해 유도되는 분포 $\tilde{p}_G$를 다시 구합니다. 그러면 $\tilde{p}_G$는 $p _{(I, J)}$에 가깝게 되기 때문에 이후 샘플링 알고리즘의 수렴 속도가 빨라집니다. 추가적인 분류기의 학습없이 IMH 알고리즘을 동작시키기 위해서 $p_G(G(z)) / \tilde{p}_G(G(z)) \approx C \cdot p_z(z) / \tilde{p}_z(z)$로 근사하고 $\tilde{p}_z$를 가우시안 믹스쳐같은 확률 모델로 두면 적절한 acceptance probability를 다음 식을 통해서 계산할 수 있습니다.

\[\tilde{\alpha}(x', x) = \min\left(1, \frac{p_{(I,J)}(x')/\tilde{p}_G(x')}{p_{(I,J)}(x)/\tilde{p}_G(x)}\right) \approx \min\left(1,\frac{r_{(I,J)}(x')({D_v^\ast(x)}^{-1}-1)p_z(z')/\tilde{p}_z(z')}{r_{(I,J)}(x)({D_v^\ast(x')}^{-1}-1)p_z(z)/\tilde{p}_z(z)}\right)\]

이 트릭을 응용해서 속성을 한 개씩 증가시키면서 잠재 변수 피팅을 반복할 수도 있습니다. 예를 들어, 검은 머리 남성 이미지를 생성하기 위해서 먼저 검은 머리 샘플에 대한 잠재 변수 피팅을 하고 다시 검은 머리 샘플 안에서 검은 머리 남성 이미지에 대한 잠재 변수를 피팅을 하는 방식입니다. 이런 방법은 큰 속성 수에 대해서 샘플링 알고리즘의 적용하는데 걸리는 시간을 크게 줄여줍니다. 아래 그림은 B, M, S, A, N, W 속성이 주어졌을 때 잠재 변수 피팅을 여러번해서 B+M+S-A-N-W 클래스를 찾는 과정을 묘사합니다.

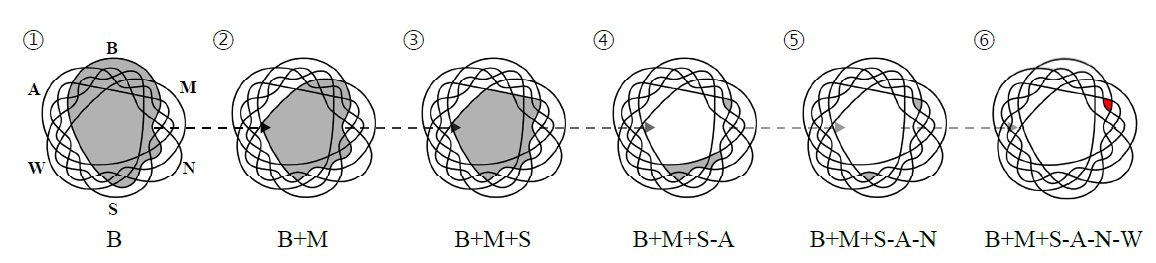
잠재 변수 피팅을 반복해서 B+M+S-A-N-W 클래스 샘플을 찾는 과정

결과

아래 결과는 검은 머리(B), 남성(M), 웃음(S) 속성이 주어졌을 때 여러 멀티 레이블 생성 결과를 보여줍니다.

머리(B), 남성(M), 웃음(S) 속성이 주어졌을 때 S2M sampling 결과

단점 및 향후 방향

논문은 단일 양성 레이블을 이용한 생성 문제를 이해시키고 풀 수 있음을 보이는데 초점을 맞추고 있습니다. 제시한 방법론은 모델이 생성하지 못 하는 샘플을 얻을 수 없습니다. 속성의 수가 증가할수록 학습 데이터 셋에서 해당 클래스의 이미지 수가 급격하게 적어지기 때문에 샘플 효율이 안 좋아지거나 이미지 퀄리티가 크게 감소합니다. 이러한 문제 때문에 실험 세팅에서는 최대 6개의 속성을 사용하였습니다. 논문에서 제시한 문제를 푸는데 더 적절한 생성 모델이나 샘플링 알고리즘이 있을 것이라고 생각합니다. 예를 들어, Langevin Dynamic 같이 타겟 분포 쪽으로 gradient update를 하는 샘플링 방식을 사용한다거나 diffusion 모델, clustering-based GANs 등을 응용해볼 수 있을 것 같습니다.

참고문헌

Mining Multi-Label Samples from Single Positive Labels