Denoising Diffusion Probabilistic Models 수학적 분석
이번 글에서는 요즘 CV에서 가장 핫한 토픽인 diffusion model 중에서 가장 기본이 되는 DDPM (https://arxiv.org/pdf/2006.11239.pdf)에 대해서 자세히 알아보려고 합니다.
※ inline으로 표현이 안되는 수식이 많아서 쓸데없이 글이 늘어지는 점 양해 부탁드립니다.
Overview

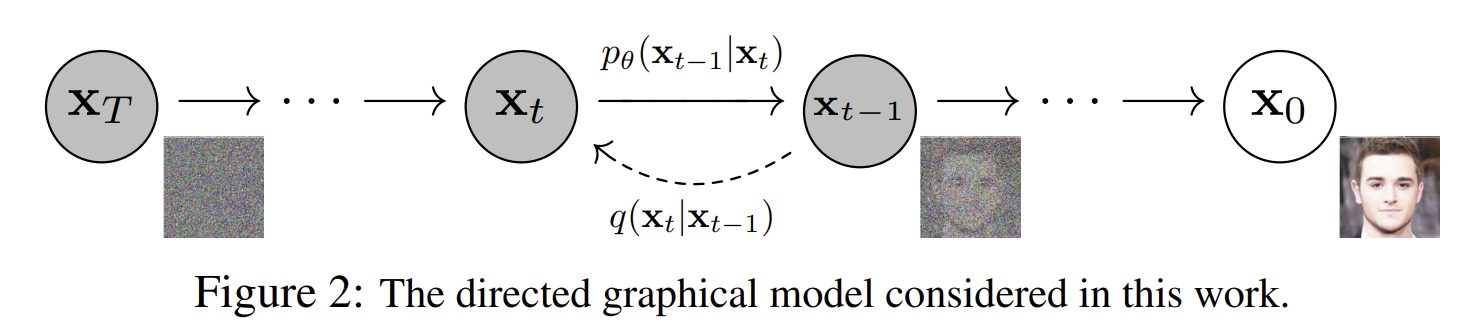
DDPM은 간단하게 말해서 data인 $x_0$에 gaussian noise를 순차적으로 추가하는 forward process를 거쳐 gaussian noise인 $x_T$를 만들어내고, 다시 random gaussian noise $x_T$로부터 gaussian noise를 순차적으로 제거하는 reverse process를 거쳐 생성하고자 하는 이미지 $x_0$를 생성해내는 모델입니다.
더 자세한 내용은 DDPM을 소개한 다른 글들이 많으니 그를 참고하시면 좋을 것 같습니다. 이 글에서는 forward process, reverse process, loss function을 수학적으로 깊게 유도해보는 것에 중점을 두겠습니다.
Forward process
먼저 forward process에 대해 알아보겠습니다. forward process는 $x_{t-1}$에서 $x_t$를 생성하는 과정의 연속이라고 이해하면 됩니다. 이를 아래와 같은 확률 분포로 모델링할 수 있습니다.
\[(1) \qquad q(x_t|t_{t-1}):=N(x_t; \sqrt{(1-\beta_t)} \cdot x_{t-1}, \beta_t \cdot I)\] \[(2)\qquad q(x_{1:T}|x_0) := \Pi^{T}_{t=1}q(x_t|x_{t-1})\]forward process를 위와 같이 가우시안 분포로 정의되는 이유는 단순히 그렇게 정의했기 때문입니다. 우리가 forward process를 원본 그림인 $x_0$에서 가우시안 noise를 계속 가하면서 $x_T$를 생성하는 과정이라고 정의했기 때문에 위와 같이 가우시안 분포 $q$로 모델링할 수 있습니다.
추가로 $\alpha_t := 1-\beta_t$, $\bar{\alpha_{t}} := \Pi^t_{s=1} \alpha_{s}$ 라고 정의하겠습니다.
(1) 에 의해 $x_t=\sqrt{1-\beta_t} \cdot x_{t-1} + \sqrt{\beta_t} \cdot z_{t-1}$ 라고 표현할 수 있습니다. ($z \sim N(0, 1)$)
위 식을 $\alpha$ 를 이용해 표현해보겠습니다.
\[x_t=\sqrt{\alpha_t} \cdot x_{t-1} + \sqrt{1-\alpha_t} \cdot z_{t-1}\] \[x_t=\sqrt{\alpha_t} \cdot (\sqrt{\alpha_{t-1}} \cdot x_{t-2} + \sqrt{1-\alpha_{t-1}} \cdot z_{t-2}) + \sqrt{1-\alpha_t} \cdot z_{t-1}\] \[x_t=\sqrt{\alpha_t \cdot \alpha_{t-1}} \cdot x_{t-2} + \sqrt{\alpha_{t-1}} \cdot \sqrt{1-\alpha_{t-1}} \cdot z_{t-2}+ \sqrt{1-\alpha_t} \cdot z_{t-1}\]이때, $X \sim N(\mu_X, \sigma_X^2)$, $Y \sim N(\mu_Y, \sigma_Y^2)$ 이면 $Z=X+Y \sim N(\mu_X+\mu_Y, \sigma_X^2 + \sigma_Y^2)$ 임을 이용하면,
\[\sqrt{\alpha_{t-1}} \cdot \sqrt{1-\alpha_{t-1}} \cdot z_{t-2}+ \sqrt{1-\alpha_t} \cdot z_{t-1} = \sqrt{\alpha_t(1-\alpha_{t-1}) + 1 - \alpha_t} \cdot \hat{z}_{t-2} = \sqrt{1 - \alpha_t \cdot \alpha_{t-1}} \cdot \hat{z}_{t-2}\]입니다.
이를 이용해서 $x_t$ 에 관한 식을 다시 풀어보겠습니다.
\[x_t=\sqrt{\alpha_t \cdot \alpha_{t-1}} \cdot x_{t-2} + \sqrt{1 - \alpha_t \cdot \alpha_{t-1}} \cdot \hat{z}_{t-2}\] \[x_t=\sqrt{\alpha_t \cdot \alpha_{t-1} \cdot \alpha_{t-2}} \cdot x_{t-3} + \sqrt{1 - \alpha_t \cdot \alpha_{t-1} \cdot \alpha_{t-2}} \cdot \hat{z}_{t-3}\]귀납적으로 풀어보면 아래와 같습니다.
\[(3) \qquad x_t=\sqrt{\bar{\alpha}_t} \cdot x_0 + \sqrt{1 - \bar{\alpha}_t} \cdot \hat{z}_0\]따라서 $\hat{z} \sim N(0, I)$ 이므로
\[(4) \qquad q(x_t|x_0)=N(x_t;\sqrt{\bar{\alpha}_t} \cdot x_0 , (1 - \bar{\alpha}_t) \cdot I)\]가 성립합니다.
Reverse process
reverse process는 forward process와 유사하지만 방향이 반대입니다. 즉 $x_t$에서 $x_{t-1}$를 생성하는 과정의 연속입니다. 논문에서는 아래와 같이 정의하고 있습니다.
Markov chain with learned Gaussian transitions starting at $p(x_T)=N(x_T;0, I)$
forward process를 확률 분포 $q$로 모델링했던 것과 같이 reverse process도 아래와 같이 확률 분포로 모델링할 수 있습니다.
\[(5) \qquad p_\theta(x_{0:T}):=p(x_T) \cdot \Pi^T_{t=1}p_\theta(x_{t-1}|x_t)\] \[(6) \qquad p_\theta(x_{t-1}|x_t):= N(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))\]이때 $p_\theta$는 왜 가우시안 분포로 정의되는 걸까요? 이는 앞서 forward process에서 $\beta_t$가 매우 작을 경우에 $p_\theta$가 $q$와 같은 형태의 분포를 가지기 때문이라고 합니다.
Loss function
DDPM의 학습 과정은 VAE에서와 유사하게 negative log likelihood의 variational bound를 최적화하는 과정입니다. 식으로 나타내보면 아래와 같습니다.
\[E[-\log p_\theta(x_0)]\leq E_q[-\log { {p_\theta(x_{0:T})}\over{q(x_{1:T}|x_0)}}]\]위 식은 (2)와 (5)에 의해서 아래와 같이 표현됩니다.
\[E[-\log p_\theta(x_0)]\leq E_q[-\log { {p_\theta(x_{0:T})}\over{q(x_{1:T}|x_0)}}] = E_q[{ {p(x_T) \cdot \Pi^T_{t=1}p_\theta(x_{t-1}|x_t)}\over{\Pi^{T}_{t=1}q(x_t|x_{t-1}) }}]\]이 식을 정리해서 아래와 같이 loss function L을 정의할 수 있습니다.
\[(7) \qquad L:= E_q[-\log p(x_T) \cdot-\Sigma^T_{t=1}\log{ {p_\theta(x_{t-1}|x_t)}\over{q(x_t|x_{t-1})}}]\](7)은
\[q(x_t|x_{t-1})\]에 관한 식입니다. 이를
\[q(x_{t-1}|x_{t}, x_0)=q(x_t|x_{t-1}) \cdot { {q(x_{t-1}|x_0)}\over{q(x_t|x_0)}}\]를 이용해서
\[q(x_{t-1}|x_{t}, x_0)\]에 관한 식으로 변환해보겠습니다.
\[L = E_q[-\log p(x_T) -\Sigma_{t>1}\log{ {p_\theta(x_{t-1}|x_t)}\over{q(x_t|x_{t-1})}}-\log{ {p_\theta(x_0|x_1)}\over{q(x_1|x_0)}}]\] \[L = E_q[-\log p(x_T) -\Sigma_{t>1}\log{ {p_\theta(x_{t-1}|x_t) \cdot q(x_{t-1}|x_0)}\over{q(x_{t-1}|x_{t}, x_0) \cdot q(x_t|x_0)}}-\log{ {p_\theta(x_0|x_1)}\over{q(x_1|x_0)}}]\] \[L = E_q[-\log p(x_T) -\Sigma_{t>1}\log{ {p_\theta(x_{t-1}|x_t)}\over{q(x_{t-1}|x_{t}, x_0)}} -\Sigma_{t>1}\log{ {q(x_{t-1}|x_0)}\over{q(x_t|x_0)}} -\log{ {p_\theta(x_0|x_1)}\over{q(x_1|x_0)}}]\] \[L = E_q[-\log p(x_T) -\Sigma_{t>1}\log{ {p_\theta(x_{t-1}|x_t)}\over{q(x_{t-1}|x_{t}, x_0)}} -\log{ {q(x_1|x_0)}\over{q(x_T|x_0)}} -\log{ {p_\theta(x_0|x_1)}\over{q(x_1|x_0)}}]\] \[L = E_q[-\log{ {p(x_T)}\over{q(x_T|x_0)}} -\Sigma_{t>1}\log{ {p_\theta(x_{t-1}|x_t)}\over{q(x_{t-1}|x_{t}, x_0)}} -\log{p_\theta(x_0|x_1)}]\]위와 같이
\[q(x_{t-1}|x_{t}, x_0)\]에 관한 식으로 변환된 Loss function L을 KL divergence (Kullback-Leibler divergence)로 나타내면 (8)이 됩니다.
\[(8) \qquad L = E_q[D_{KL}(q(x_T|x_0)||p(x_T)) + \Sigma_{t>1}D_{KL}(q(x_{t-1}|x_t, x_0)||p_\theta(x_{t-1}|x_t)) -\log{p_\theta(x_0|x_1)}]\](8)은 우리가 알고 싶은
\[p_\theta(x_{t-1}|x_t)\]를 tractable한
\[q(x_{t-1}|x_t, x_0) \quad (forward \quad process \quad posteriors)\]와 직접적으로 비교하고 있습니다.
$q(x_{t-1}|x_t, x_0)$
\[q(x_{t-1}|x_t, x_0)\]는
\[q(x_t|x_{t-1}), \quad q(x_{t-1}|x_0), \quad q(x_t | x_0)\]가 모두 gaussian (by (1), (4)) 임을 이용해서 아래와 같이 표현할 수 있습니다.
\[(9) \qquad q(x_{t-1}|x_t, x_0):= N(x_{t-1}; \tilde{\mu}_t(x_t, x_0), \tilde{\beta}_t \cdot I)\] \[(10) \qquad where \quad \tilde{\mu}_t(x_t, x_0):={\sqrt{\bar{\alpha}_{t-1}} \cdot \beta_t \over 1-\bar{\alpha}_t}\cdot x_0 + {\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})\over 1-\bar{\alpha}_t} \cdot x_t \quad and \quad \tilde{\beta}_t:={1-\bar{\alpha}_{t-1}\over 1-\bar{\alpha}_t} \cdot \beta_t\](9)와 (10)으로 표현할 수 있는 이유는 아래와 같습니다.
$proof)$
(1)과 (4)에 의해
\[q(x_t|x_{t-1}), \quad q(x_{t-1}|x_0), \quad q(x_t | x_0)\]가 모두 gaussian 이며,
\[q(x_{t-1}|x_{t}, x_0)=q(x_t|x_{t-1}) \cdot { {q(x_{t-1}|x_0)}\over{q(x_t|x_0)}}\]가 성립하기 때문에
\[q(x_{t-1}|x_{t}, x_0)\]또한 gaussian 임
\[1) \qquad q(x_t|t_{t-1}):=N(x_t; \sqrt{(1-\beta_t)} \cdot x_{t-1}, \beta_t \cdot I) \qquad by \quad (1)\] \[2) \qquad q(x_{t-1}|x_0)=N(x_{t-1};\sqrt{\bar{\alpha}_{t-1}} \cdot x_0 , (1 - \bar{\alpha}_{t-1}) \cdot I) \qquad by \quad (4)\] \[3) \qquad q(x_t|x_0)=N(x_t;\sqrt{\bar{\alpha}_t} \cdot x_0 , (1 - \bar{\alpha}_t) \cdot I) \qquad by \quad (4)\]1), 2), 3)에 의해
\[q(x_{t-1}|x_t, x_0)={1 \over \sqrt{2\pi \beta_t{1-\bar{\alpha}_{t-1} \over 1-\bar{\alpha}_t }}} \exp (-{(x_t - \sqrt{1-\beta_t} \cdot x_{t-1})^2\over 2 \beta_t} -{(x_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \cdot x_0)^2\over 2(1-\bar{\alpha}_{t-1})} -{(x_t - \sqrt{\bar{\alpha}_t} \cdot x_0)^2\over 2(1-\bar{\alpha}_t)})\]가 성립합니다.
위 정규분포식을 풀면 (10) 식이 도출됩니다.
Loss function 간소화
\[(8) \qquad L = E_q[D_{KL}(q(x_T|x_0)||p(x_T)) + \Sigma_{t>1}D_{KL}(q(x_{t-1}|x_t, x_0)||p_\theta(x_{t-1}|x_t)) -\log{p_\theta(x_0|x_1)}]\]식 (8)은 ddpm에서 사용하는 loss function입니다. 위 함수를 앞으로 아래와 같이 3가지 부분으로 나누어 간소화해보도록 하겠습니다.
\[L_T=D_{KL}(q(x_T|x_0)||p(x_T))\] \[L_{t-1}=D_{KL}(q(x_{t-1}|x_t, x_0)||p_\theta(x_{t-1}|x_t))\] \[L_0=-\log{p_\theta(x_0|x_1)}\]$L_T : \beta_t$ 고정
논문에서는 forward process에서 $\beta_t$ 를 reparametreization을 학습할 수 있지만, $\beta_t$ 를 constant로 고정했습니다. 예를 들어 $\beta_1=1e-4$, $\beta_T=2e-2$, linear하게 증가하도록 설정하는 형식입니다.
그럼 $\beta_t$ 뿐만 아니라 그로 표현되는 $\alpha_t$ , $\bar{\alpha_t}$ 모두 constant가 됩니다.
이로 인해
\[(4) \qquad q(x_t|x_0)=N(x_t;\sqrt{\bar{\alpha}_t} \cdot x_0 , (1 - \bar{\alpha}_t) \cdot I)\]가 결정됩니다.
따라서 $q$ 에는 learnable parameter가 전혀 없어지게 됩니다. 그러므로
\[L_T=D_{KL}(q(x_T|x_0)||p(x_T))\]와 같이 정의된 $L_T$ 도 학습 중에 constant이기에 loss function에서 없애버릴 수 있습니다.
$L_{t-1}$ 간소화
논문에서는
\[(6) \qquad p_\theta(x_{t-1}|x_t):= N(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))\]에서 $\Sigma_\theta(x_t, t)$ 를 untrained time dependent constant들인 $\sigma_t^2 \cdot I$로 정의하였습니다.
이러한 정의가 가능한 근거를 제시하기 위해 저자는 2가지 실험을 수행했습니다.
- $\sigma_t^2=\beta_t$ 로 정의하기
- 이렇게 정의하면 $x_0 \sim N(0, I)$ 인 상황에서 optimal하다고 합니다.
- 아래와 같이 정의하기
- ㅤ
- 이렇게 정의하면 $x_0$ 가 한 점으로 고정된 상황에서 optimal하다고 합니다.
위 두 가지 상황은 각각 reverse process entropy의 upper bound, lower bound에 해당합니다. 이 2가지 상황에서 유사한 결과가 나왔기 때문에 저자는 $\Sigma_\theta(x_t, t) = \sigma_t^2 \cdot I$ 로 정의하는 것이 가능하다고 설명하고 있습니다.
따라서 식 (6)은 아래와 같이 변환됩니다.
\[(11) \qquad p_\theta(x_{t-1}|x_t)= N(x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2 \cdot I))\]식 (9)와 식 (11)을 이용해서
\[L_{t-1}=D_{KL}(q(x_{t-1}|x_t, x_0)||p_\theta(x_{t-1}|x_t))\]를 아래와 같이 변환할 수 있습니다.
\[(12) \qquad L_{t-1}=E_q[{1 \over 2\sigma_t^2} ||\tilde{\mu}_t(x_t, x_0) - \mu_\theta(x_t, t)||^2] +C\]이때 $C$ 는 $\theta$ 와 무관하여 constant인 값들을 의미합니다.
식 (12)를 보면 우리가 구하고자 하는 $\mu_\theta$ 를 parameterization 하는 가장 단순한 방법은 $\tilde{\mu}_t$ 를 예측하도록 모델링하는 것일 겁니다.
\[(4) \qquad q(x_t|x_0)=N(x_t;\sqrt{\bar{\alpha}_t} \cdot x_0 , (1 - \bar{\alpha}_t) \cdot I)\]를 reparameterizing하면,
\[(13) \qquad x_t(x_0, \epsilon)=\sqrt{\bar{\alpha_t}} \cdot x_0 + \sqrt{1-\bar{\alpha}_t} \cdot \epsilon \quad for \quad \epsilon \sim N(0, I)\]이 됩니다.
식 (13)을
\[(10) \qquad \tilde{\mu}_t(x_t, x_0)={\sqrt{\bar{\alpha}_{t-1}} \cdot \beta_t \over 1-\bar{\alpha}_t}\cdot x_0 + {\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})\over 1-\bar{\alpha}_t} \cdot x_t\]에 대입하면,
\[(14) \qquad \tilde{\mu}_t(x_t(x_0, \epsilon), {1 \over \sqrt{\bar{\alpha}_t}}(x_t(x_0, \epsilon)-\sqrt{1-\bar{\alpha}_t} \cdot \epsilon))\] \[={\sqrt{\bar{\alpha}_{t-1}} \cdot \beta_t\over 1-\bar{\alpha}_t} \cdot {1 \over \sqrt{\bar{\alpha}_t}}(x_t(x_0, \epsilon)-\sqrt{1-\bar{\alpha}_t} \cdot \epsilon) + {\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1}) \over 1-\bar{\alpha}_t} \cdot x_t(x_0, \epsilon)\] \[={1 \over \sqrt{\alpha_t}}({ \beta_t \over 1-\bar{\alpha}_t}+{\alpha_t(1-\bar{\alpha}_{t-1}) \over 1-\bar{\alpha}_t} )\cdot x_t(x_0, \epsilon) - {\beta_t \sqrt{1-\bar{\alpha}_t} \over 1-\bar{\alpha}_t \sqrt{\alpha_t}}\epsilon\] \[={1\over \sqrt{\alpha_t}}(x_t(x_0, \epsilon) - {\beta_t \over \sqrt{1- \bar{\alpha}_t}} \epsilon)\]식 (13)과 식 (14)를 식(12)에 대입하면,
\[(15) \qquad L_{t-1}-C=E_{x_0, \epsilon}[{1 \over 2 \sigma_t^2}|| {1 \over \sqrt{\alpha_t}}(x_t(x_0, \epsilon) - {\beta_t \over \sqrt{1-\bar{\alpha}_t}}\epsilon)-\mu_\theta(x_t(x_0, \epsilon), t) ||^2]\]가 성립합니다.
따라서 $\mu_\theta$ 는 $x_t$ 가 주어졌을 때 ${1 \over \sqrt{\alpha_t}}(x_t(x_0, \epsilon) - {\beta_t \over \sqrt{1-\bar{\alpha}_t}}\epsilon)$ 을 예측하도록 학습되게 됩니다.
이를 더욱 간소화하기 위해서 논문에서는 $\mu_\theta$ 를 아래와 같이 $x_t$ 가 주어졌을 때 $\epsilon$ 을 추론하는 $\epsilon_\theta$ 로 변환했습니다.
\[(16) \qquad \mu_\theta(x_t, t) = {1 \over \sqrt{\alpha_t}}(x_t -{\beta_t \over \sqrt{1- \bar{\alpha}_t}} \cdot \epsilon_\theta(x_t, t))\]식 (14)와 식 (16)을 식 (12)에 대입하면,
\[L_{t-1}-C=E_{x_0, \epsilon_t}[{1 \over 2 \sigma_t^2}|| {1 \over \sqrt{\alpha_t}}(x_t - {\beta_t \over \sqrt{1-\bar{\alpha}_t}}\epsilon_t)- {1 \over \sqrt{\alpha_t}}(x_t -{\beta_t \over \sqrt{1- \bar{\alpha}_t}} \cdot \epsilon_\theta(x_t, t)) ||^2]\] \[=E_{x_0, \epsilon_t}[{\beta_t^2\over 2\sigma_t^2(1-\bar\alpha_t)}|| \epsilon_t-\epsilon_\theta(x_t, t) ||^2]\] \[=E_{x_0, \epsilon_t}[{\beta_t^2\over 2\sigma_t^2(1-\bar\alpha_t)}|| \epsilon_t-\epsilon_\theta(\sqrt{\bar\alpha_t} \cdot x_0 + \sqrt{1-\bar\alpha_t} \cdot \epsilon_t, t) ||^2] \quad by \quad (3)\] \[=E_{x_0, \epsilon}[{\beta_t^2\over 2\sigma_t^2(1-\bar\alpha_t)}|| \epsilon-\epsilon_\theta(\sqrt{\bar\alpha_t} \cdot x_0 + \sqrt{1-\bar\alpha_t} \cdot \epsilon, t) ||^2]\]최종 loss function
논문에서는 최종적인 loss function으로 위 결과에서 계수를 무시한 아래와 같은 식을 사용합니다.
\[L=E_{x_0, \epsilon}[|| \epsilon-\epsilon_\theta(\sqrt{\bar\alpha_t} \cdot x_0 + \sqrt{1-\bar\alpha_t} \cdot \epsilon, t) ||^2]\]위 식처럼 계수를 제외하는 것이 더욱 학습이 잘되는데 그 이유는 전체 timestep에서 가해지는 noise의 크기가 일정하게 반영되기 때문인 것 같습니다.
이미지 생성 과정
식 (16)을 이용하면 식 (11)과 같은
\[p_\theta(x_{t-1}|x_t)\]에서 $x_{t-1}$ 을 sampling하는 것을
\[x_{t-1} = {1 \over \sqrt{\alpha_t}}(x_t -{\beta_t \over \sqrt{1- \bar{\alpha}_t}} \cdot \epsilon_\theta(x_t, t)) + \sigma_t \cdot z \quad where \quad z \in N(0, I)\]로 계산할 수 있습니다.
따라서 random gaussian noise인 $x_T$ 부터 순차적으로 $x_0$ 를 생성해낼 수 있습니다.
Summary

지금까지의 내용을 잘 따라오셨다면 논문에 소개된 Training algorithm과 Sampling algorithm이 어떤 의미인지를 충분히 이해하실 수 있을 것이라 생각합니다. 워낙 유명하고 핫한 주제라 구현된 라이브러리나 코드가 많으니 그를 참고해보시는 것도 추천드립니다.