WaveBound: Dynamic Error Bounds for Stable Time Series Forecasting (NeurIPS'22) 눈문 소개

machine-learning

올해 11월 말에 열릴 머신러닝 학회인 NeurIPS 2022에 제가 제출했던 논문 “WaveBound: Dynamic Error Bounds for Stable Time Series Forecasting”이 어셉되어서 리뷰하고자 합니다.

소개

시간의 흐름에 따라 순차적으로 기록된 데이터를 시계열 데이터라고 부릅니다. 시계열 예측은 과거 시계열 데이터로부터 미래를 예측하는 테스크로 교통 속도 예측, 에너지 사용량 예측 등 다양한 분야에서 주목을 받아왔습니다. 최근에는 Informer, Autoformer와 같은 딥러닝 기반 시계열 예측 모델이 주목받았지만 본 연구에서 이러한 모델은 여전히 과적합에 취약함을 보여주었습니다.

기존 딥러닝 모델의 과적합 문제를 완화하기 위해서 학습 로스를 일정 값 이하로 낮추지 않는 Flooding 이라는 regularization 기법이 소개된 바가 있습니다. 본 논문에서는 Flooding을 시계열 예측 모델에 적합하도록 개선한 regularization 기법인 WaveBound를 소개합니다. WaveBound는 Flooding과 다르게 각 출력 변수 마다 적절한 학습 로스 하한을 설정할 수 있습니다. 이러한 방법을 통해 다양한 시게열 데이터 셋에서 딥러닝 기반 시계열 예측 모델의 과적합 문제를 완화할 수 있음을 보여줍니다.

Flooding과 WaveBound를 사용했을 때 학습 로스를 제한하는 방법을 비교함. Flooding은 평균 로스를 제한하고 WaveBound는 각 출력 변수마다 적절한 학습 로스의 하한을 설정한다.

문제 설정

논문 이해를 돕기 위해서 시계열 예측 테스크에 대한 정의와 일반화와 관련된 몇가지 용어에 대해 먼저 정리해보겠습니다. 논문에서 주로 다룰 시계열 예측 문제는 deterministic forecasting으로 과거 시퀀스 $x^t=(z_{t-L+1}, z_{t-L+2}, …, z_t), z_i \in \mathbb{R}^K$로부터 미래 시퀀스 $y^t=(z_{t+1}, z_{t+2}, …, z_{t+M}), z_i \in \mathbb{R}^K$를 예측하는 모델 $g:\mathbb{R}^{L\times K}\rightarrow \mathbb{R}^{M\times K}$를 배우는 것입니다. 여기서 $M$, $L$은 각각 출력, 입력 시퀀스 길이고 $K$는 변수 개수(시퀀스 개수)입니다.

로스 함수 $\ell$이 주어졌다고 합시다. 데이터 분포 $p(x,y)$ 가 있을 때, 우리가 최종적으로 줄이고자 하는 목표인 risk는 $R(g) := \mathbb{E}_{(x, y) \sim p(x, y)} \left[\ell(g(x), y) \right]$ 로 정의됩니다. 하지만 우리는 $p$ 에 대해서 정확히 알 수 없기 때문에 학습 데이터셋 $ \mathcal{X} := {(x_i, y_i)} _{i=1} ^N $ 에서 로스의 샘플 평균을 계산하여 사용하게 됩니다. 이를 empirical risk라고 부르고 $\hat{R}(g) := \frac{1}{N}\sum _{i=1} ^N \ell(g(x_i), y_i)$ 로 정의됩니다.

본 논문에서는 error가 independent identically distributed 되어있다고 가정하고 MSE 로스를 사용하는 경우를 주로 다룹니다. risk와 empirical risk는 다음과 같이 각 스탭, 피쳐(시퀀스 종류)에서 발생하는 risk, empirical risk의 항들로 분해를 할 수 있습니다.

\[R(g) = \mathbb{E}_{(u,v)\sim p(u, v)} \left[ \frac{1}{MK} \lVert g(u)-v \rVert^2 \right ] = \frac{1}{MK}\sum_{j,k}R_{jk}(g), \\ \hat{R}(g) = \frac{1}{NMK}\sum_{i=1}^N \lVert g(x_i)-y_i \rVert^2= \frac{1}{MK}\sum_{j,k}\hat{R}_{jk}(g),\]

여기서 $R _{jk} (g) := \mathbb{E} _{ (u,v) \sim p(u, v) } \left[ \lVert g _{jk}( u ) - v _{jk} \rVert^2 \right]$이고 $\hat{R} _{jk}(g) := \frac{1}{N} \sum _{i=1}^N \lVert g _{jk}(x_i) -(y_i) _{jk} \rVert^2$입니다.

Flooding

Flooding은 학습 로스를 일정 값 이하로 낮추지 않게 해서 일반화 성능을 올리는 기법입니다. 구체적으로 empirical risk를 최소화 하는대신 아래와 같이 상수 $b$를 사용하여 정의한 flooded empirical risk를 최소화합니다.

\[\hat{R}^{fl}(g) = | \hat{R}(g) - b | + b.\]

여기서 $b$는 하이퍼파라미터로써 validation 데이터셋을 이용하여 적절한 값을 찾아주어야 합니다. 절댓값 뒤에 더하는 $b$는 gradient update를 할 때 아무런 영향을 주지 않지만 MSE 분석에서 유용하게 쓰입니다.

Risk를 최소화 하도록 모델 파라미터의 그레디언트 업데이트를 할 때, $\hat{R}(g)>b$ 인 경우에 $\hat{R}^{fl}(g)$와 $\hat{R}(g)$가 같은 그레디언트 방향으로 최소화하게 되고 그렇지 않은 경우에는 반대 그레디언트 방향으로 업데이트를 하게 됩니다. $b$를 $R(g)>b$하도록 잡은 경우 flooded empirical risk가 empirical risk보다 (estimator의) MSE가 작다는 것이 증명되어 있습니다.

딥러닝 모델을 학습할 때 메모리가 무한정하지 않으므로 미니 배치 최적화를 하게 됩니다. 전체 학습 데이터가 T개의 미니 배치로 이루어져 있고 $\hat{R}_t(g)$를 t번째 미니 배치에 대한 empirical risk라고 두면 Jensen 부등식에 의해서 다음이 성립합니다.

\[\hat{R}^{fl}(g) \leq \frac{1}{T} \sum _{t=1}^{T} (| \hat{R}_t(g) - b | + b).\]

즉, 미니 배치 최적화는 flooded empirical risk의 상한을 감소시키게 됩니다.

시계열 예측 문제에서 Flooding의 단점

Flooding을 시계열 예측 문제에 바로 적용하기에는 몇 가지 문제가 있습니다.

첫 번째로 미래 예측 스탭에서 대체로 큰 에러가 발생하기 때문에 flooding은 해당 부분에 집중하여 에러의 하한을 설정해야 하는 점이 있습니다. 아래 식처럼 각 출력 컴포넌트에 대한 risk 항들로 flooded empirical risk를 표현해보면 $\hat{R}_{jk}(g)$들의 평균을 $b$로 바운드하게 됨을 알 수 있습니다.

\[\hat{R}^{fl}(g) = \left| \hat{R}(g) - b \right| + b = \left|\left(\frac{1}{MK}\sum _{j,k}\hat{R}_{jk}(g)\right)-b\right|+b.\]

데이터가 충분히 많지 않은 경우 학습 과정에서 큰 에러가 발생하는 출력 변수에 민감하게 되어 다른 변수는 regularization 효과를 잘 받지 못 할 수 있습니다.

두 번째로는 시계열 데이터는 노이즈가 심한 경우가 많기 때문에 각 배치마다 에러의 정도가 다르기 쉽다는 점이 있습니다. $\hat{R}_t(g)-b$, $t \in {1,2,…,T}$이 크게 다를 경우 위의 Jensen 부등식이 tight하지 않게 되기 때문에 제대로 학습이 되지 않을 수 있습니다.

WaveBound

위 문제를 해결하기 위해서 WaveBound는 EMA 모델을 활용해서 (1) 각 출력 변수마다 적절한 하한을 설정하고, (2) 배치마다도 적절한 하한를 설정하는 방법을 제안합니다.

구체적으로 소스 네트워크 $g_\theta$와 타겟 네트워크 $g_\tau$를 사용하는데 두 네트워크는 같은 아키텍쳐이고 파라미터만 $\theta$, $\tau$로 다릅니다. 그러면 타겟 네트워크는 소스 네트워크에서 발생하는 에러의 하한을 예측하게 되고 파리미터 $\tau$는 아래같이 $\theta$의 exponential moving average를 취해서 업데이트하게 됩니다.

\[\tau \leftarrow \alpha\tau + (1-\alpha)\theta\]

여기서 $\alpha$는 decay 정도를 나타내는 하이퍼파라미터로 일반적으로 0.99, 0.999, … 같은 값을 사용합니다. 실험에서는 업데이트 속도가 너무 느려지지 않게 0.99를 사용했습니다.

소스 네트워크는 다음과 같이 정의되는 wave empirical risk $\hat{R}^{wb}(g _\theta)$를 최소화하도록 업데이트됩니다.

\[\hat{R}^{wb}(g _\theta) = \frac{1}{MK} \sum _{j,k} \hat{R}^{wb} _{jk}(g _\theta), \\ \hat{R}^{wb} _{jk}(g _\theta) = \left|\hat{R} _{jk}(g _\theta) - (\hat{R} _{jk}(g _\tau) - \epsilon) \right| + (\hat{R} _{jk}(g _\tau) - \epsilon),\]

여기서 $\epsilon$은 하이퍼파라미터로 소스 네트워크의 에러가 타겟 네트워크의 에러로부터 얼마나 멀어질 수 있는지 허용폭을 나타냅니다. 이 값을 음의 방향으로 큰 값을 설정하면 학습 진행이 안될 수 있기 때문에 실험에서는 0.01 혹은 0.001 정도로 작은 양수 값을 사용했습니다.

타겟 네트워크는 학습 중간에 얻어지는 소스 네트워크를 앙상블하는 효과가 있다고 알려져 있습니다. (SWA 논문, Mean teacher 논문 참고) 이 때문에 소스 네트워크에 비해 노이즈에 견고한 학습을 할 수 있고 irreducible error 밑으로 학습 에러를 쉽게 낮추지 않을 것이라 예상할 수 있습니다. 따라서 타겟 네트워크를 소스 네트워크의 각 출력 변수의 학습 에러 하한을 지정해주는 용도로 사용할 수 있을 것입니다.

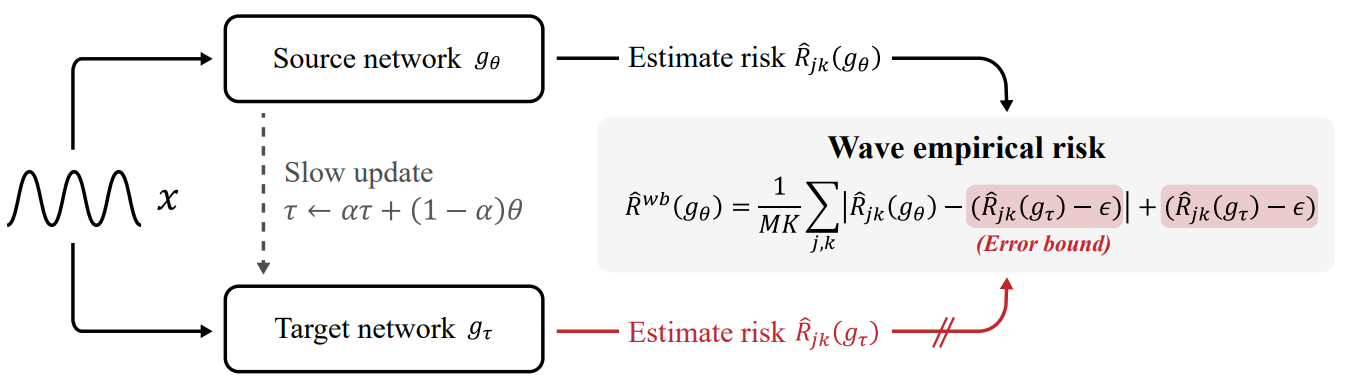
WaveBound 학습 방식 요약

WaveBound는 다음과 같은 유용한 성질을 가지고 있습니다.

Wave empirical risk의 미니 배치 최적화

$(\hat{R}^{wb} _t) _{jk}(g)$와 $(\hat{R} _t) _{jk}(g)$가 각각 $t$번째 미니 배치에 대한 $j$번째 예측 스탭, $k$번째 피쳐의 wave empirical risk와 empirical risk라고 합시다. 타겟 네트워크 $g^\ast$가 주어졌을 때 Jensen 부등식에 의해 다음이 성립합니다.

\[\hat{R}^{wb} _{jk}(g) \leq \frac{1}{T} \sum _{t=1}^{T} \left(\left|(\hat{R} _t) _{jk}(g) - (\hat{R} _t) _{jk}(g^\ast) + \epsilon \right| + (\hat{R} _t) _{jk}(g^\ast) - \epsilon\right) = \frac{1}{T} \sum _{t=1}^{T}(\hat{R}^{wb} _t) _{jk}(g).\]

따라서 미니 배치 최적화는 wave empirical risk의 상한을 줄여줍니다. flooded empirical risk와 다르게 $(\hat{R} _t) _{jk}(g) - (\hat{R} _t) _{jk}(g^\ast) + \epsilon$가 배치간에 비슷하기 때문에 부등식의 tight한 바운드를 기대할 수 있습니다.

Risk estimator의 정확도

다음 정리는 어떤 경우에 empirical risk에 비해 wave empirical risk가 정확한지 나타냅니다.

풀어서 설명하면 empirical risk의 MSE는 다음과 같은 조건에서 감소될 수 있습니다.

타겟 네트워크가 충분한 복잡도를 가지고 있어서 $\hat{R} _{ij}(g) - \hat{R} _{ij}(g^\ast)$, $\hat{R} _{kl}(g)$ 각 페어가 모두 독립이 되도록 하는 경우. (참고로 각 출력 변수의 error가 pairwise independent함이 충분 조건임.)
$\hat{R} _{ij}(g^\ast)-\epsilon$이 $\hat{R} _{ij}(g)$과 $R _{ij}(g)$ 사이에 있을 가능성이 높은 경우.

앞에서 이야기 했듯이 타겟 네트워크 $g^\ast$는 $g$에 비해 노이즈에 견고하고 일반화가 잘 되기 때문에 작은 $\epsilon$을 설정해서 $\hat{R} _{ij}(g^\ast)-\epsilon$이 $R _{ij}(g)$에 가깝게 설정될 수 있을 것입니다. 그러면 소스 네트워크의 각 출력 변수에서의 학습 로스는 각 변수의 테스트 로스 이하로 잘 안 떨어지게 되어 일반화가 잘 될 수 있습니다.

실험 결과

학습 로스와 테스트 로스 차이

아래 그래프는 WaveBound를 사용했을 때 전체적으로 학습 로스와 테스트 로스 사이 차이가 작아짐을 알 수 있습니다. 즉, 새로운 데이터에 대해 일반화가 잘 되도록 바뀌었다는 것을 나타냅니다.

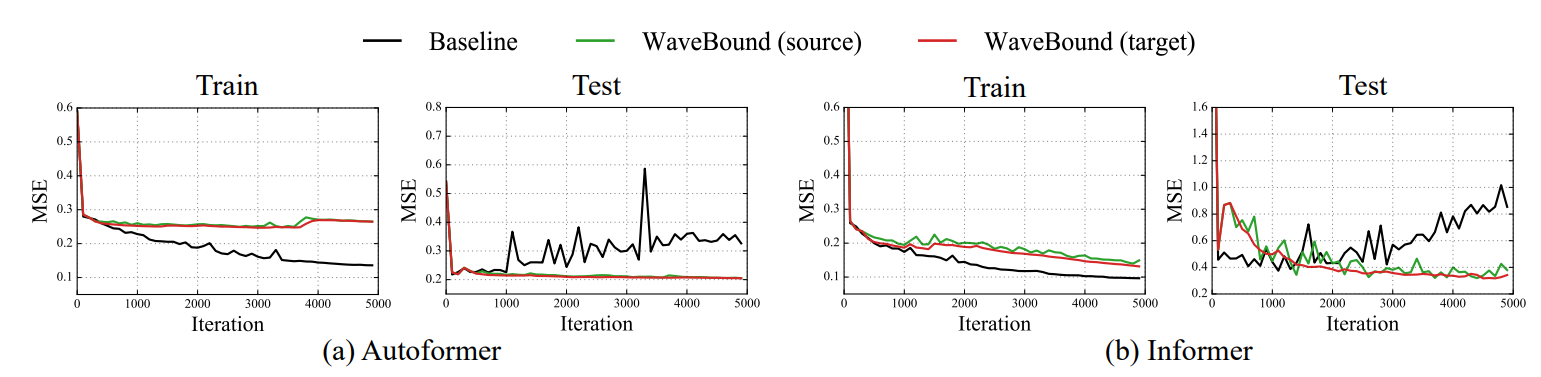
WaveBound를 사용했을 때 학습과 테스트 로스 차이가 작아짐.

Multivariate forecasting 테스크 정량 평가

아래 표는 다양한 데이터 셋에서 WaveBound를 사용했을 때 multivariate forecasting 모델의 예측 성능이 좋아짐을 보여줍니다.

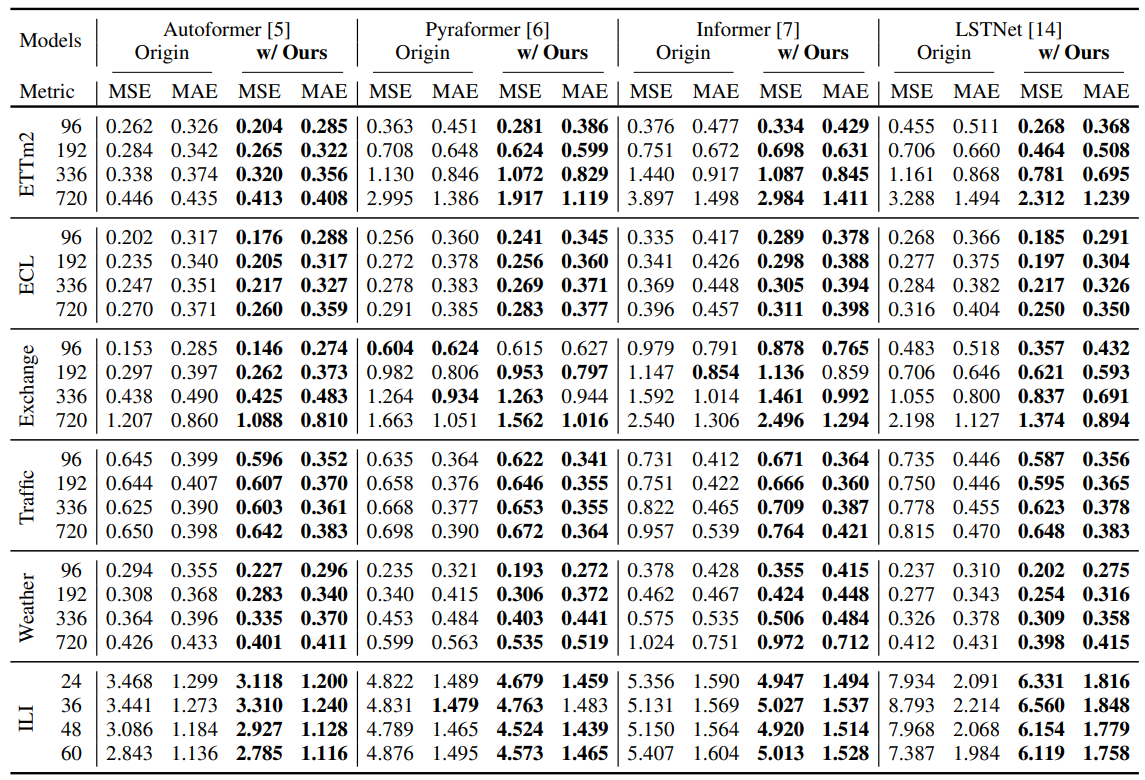
WaveBound를 사용했을 때 Multivariate forecasting 성능.

각 예측 스탭에서의 테스트 로스

아래 그림은 WaveBound가 모든 예측 스탭에서 성능을 올려주었음을 보여줍니다.

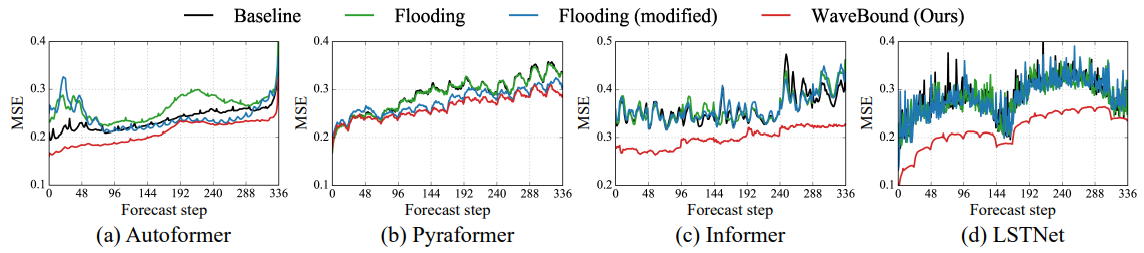
ECL 데이터셋에서 각 예측 스탭에서의 테스트 로스 평균.

Ablation study

아래 표는 다양한 형태의 empirical risk를 사용하였을 때 성능이 어떻게 달라지는지를 보여줍니다. EMA 메소드의 경우 전통을 따라 타겟 네트워크의 성능을 측정했습니다. 표에서 볼 수 있듯이 EMA 메소드를 사용했을 때 성능이 올라가고 각 변수마다 적절한 바운드를 사용하는 방식을 썼을 때 가장 성능이 좋았습니다.

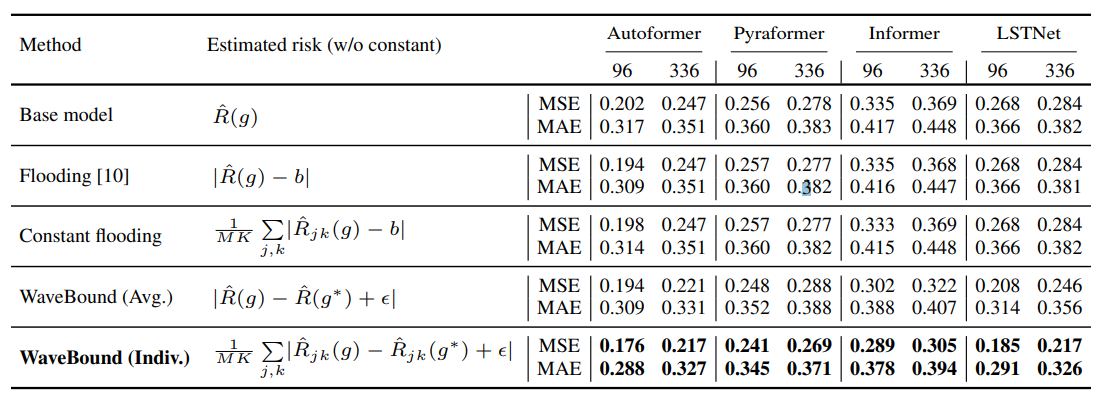
Empirical risk와 변형 식을 써서 학습했을 때 ECL 데이터 셋에서 성능 비교.

로스 모형

학습 로스가 평평한 형태일수록 일반화가 잘 되는 경향이 있다고 알려진 바가 있습니다. (이 방법론의 정확성에 대해 논쟁이 있긴 합니다.) 아래 그림은 filter normalization을 사용해서 로스의 랜드스케이프를 나타내보았습니다. WaveBound를 사용했을 경우 학습 로스가 더 평평해짐을 알 수 있습니다.

ETTh1 데이터 셋에서 학습한 예측 모델의 로스 랜드스케이프

단점 및 향후 방향

소개한 방법은 over-parametrized된 네트워크에 사용하기 적합한 방법론입니다. 안타깝게도 최근 연구(NLinear, FiLM)에 의하면 간단한 모델이 시계열 예측에 굉장히 좋은 성능을 보이고 있습니다. 따라서 본 논문이 제시한 방법이 효과적으로 사용되기 위해서는 큰 모델이 시계열 예측에 효과적임을 입증해야 할 것 같습니다.