Isogeny-based cryptography

Introduction

현재 사용되고있는 공개키 암호 시스템은 많은 수가 기본적인 RSA의 변형으로 discrete logarithm problem(이산로그) 또는 integer factorization problem 문제의 어려움을 기반으로 하고 있으며, 타원곡선 상에서의 연산에 기반한 시스템 역시 elliptic-curve discrete logarithm problem(ECDLP)을 기반으로 합니다. 이 3가지 문제들은 모두 양자컴퓨터상에서 Shor’s algorithm으로 빠른 시간에 풀 수 있음이 알려져있기 때문에, 양자컴퓨터가 등장하더라도 그 안전성을 보장할 수 있는 post-quantum cryptography algorithm이 필요하게 되었습니다.

NIST(미국 국립표준기술연구소) 에서는 양자컴퓨터의 출현에도 안전한 Post-Quantum Cryptography의 표준화를 위해 여러 알고리즘들을 제출받아서 보안성과 성능을 평가했고, 2017년부터 시작된 심사는 4개의 라운드를 거쳐 2022년에 1개의 PKE(Public-key Encryption) 및 키 생성 알고리즘과 3개의 Digital Signature 알고리즘이 선택되었습니다(링크).

Primary algorithm으로 선정된 CRYSTALS-KYBER (PKE)/CRYSTALS-DILITHIUM (Digital Signature) 은 lattice-based cryptography system이며, Learning with errors(LWE) 문제를 기반으로 합니다. 다른 알고리즘인 FALCON도 역시 격자기반 암호 시스템이라는 사실은 결국 post-quantum 시대의 표준 암호의 승자는 결국 lattice-based cryptography가 될 가능성이 현재로서는 매우 높다는 점을 시사합니다.

그러나 제가 오늘 소개할 것은 격자 기반 암호가 아닌 Elliptic Curve 상의 Isogeny라는 개념을 이용한 암호 시스템입니다. NIST의 표준화 알고리즘에 4라운드까지 뽑힌 Supersingular isogeny key exchange(SIKE)가 여기에 포함되는데요, 이 암호 시스템의 놀라운 사실은 post-quantum 시대의 표준화 알고리즘 후보까지 오른 알고리즘이 올해 여름에 일반 데스크톱 컴퓨터로도 빠른 시간 내에 공격이 가능해졌다는 것입니다.

Elliptic Curves and Cryptography

SIKE로부터 출발해서 차차 점점 쉬운 개념으로 접근하여 이해하고 다시 올라오는 방법을 사용할 것입니다. NIST에 제출된 SIKE는 기본적으로 Supersingular Isogeny Diffie-Hellman (SIDH) protocol에서 디테일만 달라진 것입니다. 여기서 Diffie-Hellman은 유명한 개념이므로 한번 짚고 넘어갑시다.

Diffie-Hellman Key Exchange란 간단하게, 두 사람 Alice와 Bob이 공개된 정수 $g$ 및 modulo $p$와 서로의 비밀키 $a, b$를 가지고 있을 때 $g^a \mod p, g^b \mod p$를 계산하여 서로에게 전달함으로써 $g^{ab} \mod p$ 라는 공통의 키를 공유하는 방법을 말합니다. 이는 discrete logarithm 문제에 의존하고 있음을 쉽게 관찰할 수 있습니다.

Elliptic Curve Diffie-Hellman 역시 비슷합니다. Elliptic Curve와 그 generator $G$가 공유되어 있을때, Alice는 비밀키 $a$에 대해 $aG$를 계산하고 Bob은 $bG$를 계산하여 서로에게 전달하면 $a(bG) = b(aG) = abG$가 성립하기 때문에 키 $abG$를 공유할 수 있습니다. Elliptic Curve Diffie-Hellman 역시 $G$와 점 $A$가 주어졌을 때 $A = aG$가 성립하는 $a$를 찾는 ECDLP 문제의 어려움을 기반으로 하고 있습니다.

이제 SIDH에서 DH부분을 알아보았고, Supersingular와 Isogeny가 무슨뜻인지 알아볼 차례입니다. 먼저 Isogeny는 두 elliptic curve $E, E’$ 사이의 map 중 특정 조건을 만족하는 map을 말합니다. 그러면 그 전에 Elliptic curve에 대해 먼저 살펴보아야 할 것입니다.

Elliptic Curve $E: y^2 = x^3 + ax + b$에서 $a, b$가 field $K$의 원소일 때 $E$ is defined over $K$ 라 하고, $E/K$로 나타냅니다. 예를 들어, $E/\mathbb{Q}: y^2 = x^3-2$는 elliptic curve이고 $(1,1), (1,-1), (3,5)$ 등을 원소로 갖습니다. 여기서 $x, y \notin \mathbb{Q}$인 원소도 elliptic curve에는 포함됩니다. Elliptic Curve 상에서의 연산으로는 덧셈($+$)이 정의되어 $(E, +)$는 abelian group을 이룹니다. 두 원소의 덧셈은 다음 그림을 따릅니다.

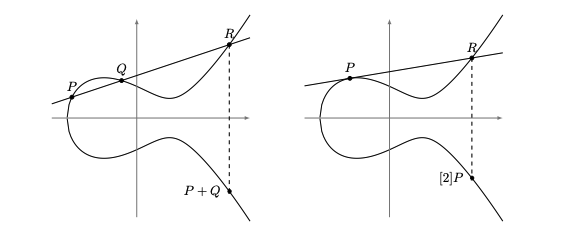
addition on elliptic curve: De Feo, 2017

실제 cryptography에 사용되는 Eliptic Curve는 보통 유한체 $\mathbb{F}{p}$ 위에서 정의되어 있습니다. $E/\mathbb{F}{13}: y^2 = x^3 + 5$는 $(2, 0), (4, 2), (4, 11)$등을 원소로 가집니다. $\mathbb{F}_{13}$ 위의 elliptic curve는 좌표평면상에서 위 그림처럼 나오지 않는데 어떻게 덧셈이 정의되는지에 대해 의문을 가질 수 있습니다. 그러나 위 그림에서 직선 $P, Q$가 $E$와 만나는 점 $R$을 계산할 때 기울기를 이용하여 교점을 구하듯 동일한 연산을 $F_p$ 위에서 적용하면 유한체 위에서도 덧셈이 잘 정의됩니다.

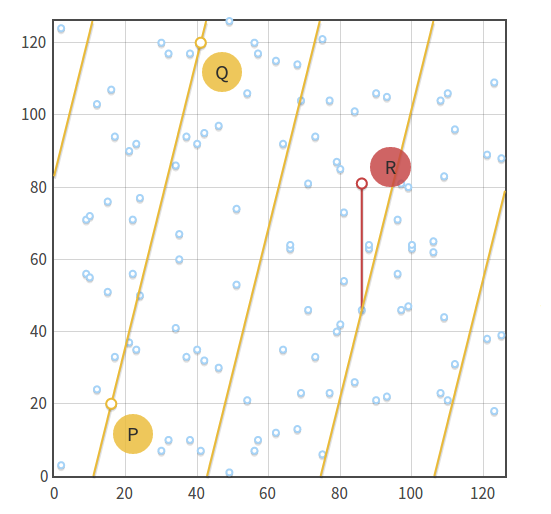
$addition on $y^2=x^3-x+3$ on $\mathbb{F}_{127}$: Andrea Corbellini, 2015$

다시 정리하자면, Elliptic Curve는 Cubic Curve이며, 덧셈연산을 위와같이 정의했을 때 Abelian group이 됩니다.

j-invariant, isomorphism, isogeny

$E: y^2 = x^3 + ax + b$의 j-invariant는 $j(E)=1728\frac{4a^3}{4a^3+27b^2}$으로 정의됩니다. 두 elliptic curve $E_1, E_2$ 사이에 (algebraically closure 위에서의) isomorphism이 존재하는 것과 둘의 j-invariant 값이 동일함은 동치임이 알려져 있습니다. 여기서 isomorphism이란 두 curve를 abelian group으로 보았을 때 group isomorphism으로, isomorphic하다는 것은 곧 덧셈연산에 대해 두 curve가 사실상 동일하다는 의미입니다. 즉, j-invariant라는 값은 curve를 결정지으므로 elliptic curve는 j-invariant 값으로 표현할 수 있습니다.

한편, isogeny는 isomorphism처럼 두 elliptic curve를 완전히 동일화시키는 강력한 map은 아니고, surjective group morphism입니다. 이것에 대해 깊이 이해하지 않고도 isogeny-based cryptography에 대해서는 다행히 공부할 수 있습니다. Isogeny-based cryptography에 사용되는 isogeny는 Separable isogeny입니다. separable isogeny는 elliptic curve의 subgroup에 대응된다는 특성을 지니고 있습니다. 즉, 주어진 subgroup에 대해 해당 subgroup을 kernel로 하는 isogeny가 유일하게 존재합니다. 그리고 Velu’s Formula를 이용해 Elliptic curve $E$, subgroup $G$를 input으로 받아 kernel이 $G$인 isogeny $\phi: E \rightarrow E’$와 codomain $E’$를 만들 수 있습니다.

원래의 Diffie-Hellman에서, $\mod p$의 multiplicative group $p^{\times}$와 generator $g$에 대해 $<g^a>$와 $<g^b>$는 subgroup이었고, 이를 이용해 $<g^{ab}>$라는 공유 키를 얻었습니다. Elliptic Curve Diffie Hellman에서는 $$와 $$를 주고받아 $$를 공유했습니다. 그러면 이와 유사하게 작동하는 어떤 것을 isogeny를 이용하여 만들 수 있을까요?

SIDH

Abelian group $E$에 대해, $P_A, Q_A, P_B, Q_B \in E$가 알려져 있다고 합시다. Alice는 $a \in \mathbb{Z}$를 골라 subgroup $A = <P_A + aQ_A>$, Bob은 $b \in \mathbb{Z}$를 골라 subgroup $B = <P_B + bQ_B>$을 계산합니다. 그리고 Velu’s formula를 이용하면 $A$를 kernel로 하는 isogeny $\varphi_A: E \rightarrow E_A$와 $B$를 kernel로 하는 $\varphi_B: E \rightarrow E_B$를 생성할 수 있습니다. 여기서 kernel에 의해 $E_A = E/A, E_B = E/B$입니다(quotient group).

Alice가 $E_A, \varphi_A(P_B), \varphi_A(Q_B)$를, Bob이 $E_B, \varphi_B(P_A), \varphi_B(Q_A)$를 서로 계산후 전달한다고 하면 Alice는 $\varphi_B(A) = \varphi_B(<P_A +aQ_A>) = <\varphi_B(P_A) + a\varphi_B(Q_A)>$를, Bob은 $\varphi_A(B) = \varphi_A(<P_B +bQ_B>) = <\varphi_A(P_B) + b\varphi_A(Q_B)>$를 계산할 수 있습니다. (isogeny는 group homomorphism이므로)

한편, $\varphi_B(A) \subset E_B$는 $E_B$의 subgroup이므로 $\varphi_B(A)$를 kernel로 하는 isogeny $\phi_B: E_B \rightarrow E_{AB}$를 생각할 수 있습니다. 마찬가지로, $\phi_A: E_A \rightarrow E_{BA}$도 만들면 $E_{AB} = E_B / \varphi_B(A), E_{BA} = E_A / \varphi_A(B)$가 됩니다. 여기서 $E_{AB}$와 $E_{BA}$의 j-invariant는 동일하다는 사실이 알려져 있습니다. 따라서, Alice와 Bob은 $j(E_{AB}) = j(E_{BA})$를 공유할 수 있게 됩니다.

Isogeny graph

앞선 설명은 사실 많은 점프가 있고 자세히 이해하기는 어려울 것입니다. 다시 큰 그림부터 천천히 좀더 알아보는 편이 좋을 것 같습니다. 일단 Isogeny라는 개념이 왜 암호시스템을 만드는데 매력적으로 다가왔던 것일까요?

Graph-walking Diffie-Hellman

Finite graph $G = (V,E)$가 주어진 상태에서 Diffie-Hellman key exchange를 한다고 생각해봅시다. starting vertex $S$가 주어져 있고, Alice와 Bob은 secret path(vertex가 정해져 있는 것은 아니므로 direction의 sequence로 볼 수 있습니다)를 가지고 있습니다. 해당 path $S$로부터 Alice path로 이동했을때 도착점 $A$와 Bob path로 이동한 도착점 $B$를 서로 공유하고, $A$에서 출발하여 Bob path로 이동한 도착점 $AB$와 $B$에서 출발하여 Alice path로 이동한 도착점 $BA$가 동일하게 된다면 둘은 $AB=BA$를 공유할 수 있을 것입니다.

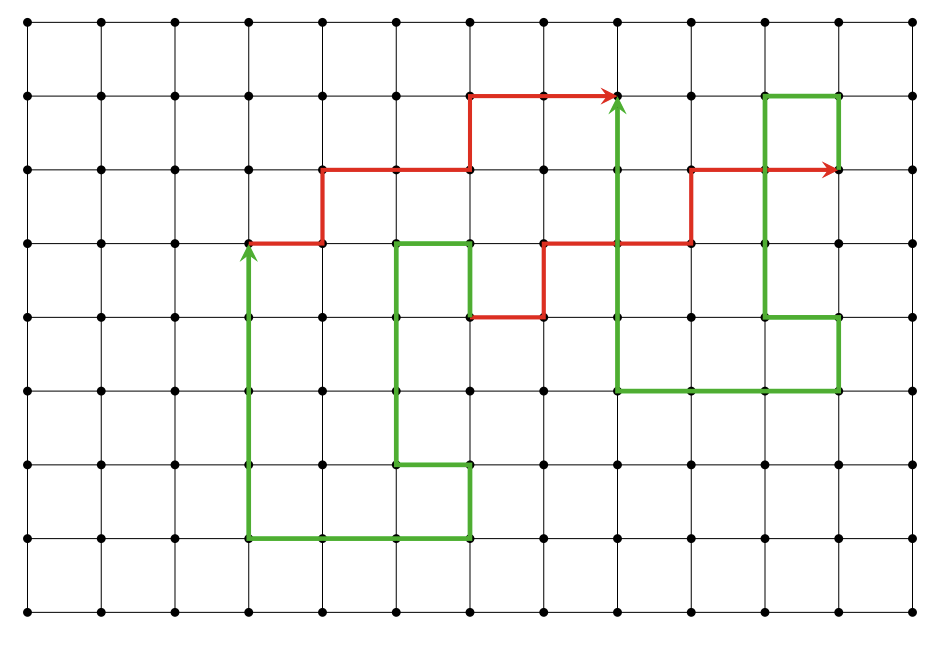
Diffie-Hellman on grid graph: Lorenz Panny, 2017

위 그림은 grid graph에서 Diffie-Hellman key exchange를 표현한 예시로, Alice의 path를 빨간색, Bob의 path를 초록색으로 나타내었습니다.

이러한 Diffie Hellman이 가능하고 안전하기 위해서는 해당 그래프가 다음과 같은 조건을 만족해야 합니다.

exponential한 크기 (vertex의 개수)
시작점과 끝점으로 path를 유추할 수 없음
Alice path, Bob path의 순서에 관계없이 동일한 vertex에 도착해야함 (AB=BA, commutativity)

그리고 Isogeny graph는 이 조건들에 부합하는 그래프였기 때문에 isogeny는 key exchange protocol을 만드는 데 눈에 띄게 됩니다. 그런데 잠시, isogeny는 eliptic curve 사이의 map이라고 배웠는데, isogeny graph는 과연 무엇일까요?

$\ell$-Isogeny graph over a field $K$ 는 다음으로 이루어진 그래프입니다.

Vertices: isomorphism classes of elliptic curves over $K$.
Edges: equivalence classes of degree-$\ell$ isogenies.

동일한 Isomorphism class에 속하는 elliptic curve는 동일하다고 볼 수 있으므로 vertex set은 $K$ 위의 elliptic curve들의 집합입니다. edge set은 $K$ 위의 elliptic curve 사이의 isogeny 중 kernel size가 $\ell$인 것들의 집합이 됩니다. 엄밀히 따지면 degree는 kernel size와 다른 개념이지만 여기서 다루는 separable isogeny들에서는 동일합니다. 예를 통해 좀더 자세히 알아봅시다.

Example(Isogeny). $m \neq 0$에 대해 multiplication-by-$m$-map $[m]: E \rightarrow E$ 는 degree-$m^2$ isogeny입니다. 이 isogeny의 kernel은 $m$-tosion 이라고 부르며 $[m]P = O$가 되는 $P$들의 집합입니다. $E$에서 m-torsion은 $E[m]$으로도 표기합니다. 일반적인 경우 $E[m]$은 $\mathbb{Z}_m \times \mathbb{Z}_m$과 isomorphic함이 알려져 있으므로 이 isogeny의 degree는 $m^2$이 됩니다.

Supersingular isogeny graph

SIDH가 실제로 동작하는 elliptic curve는 실제로 큰 소수 $p$에 대해 $\mathbb{F}_{p^2} := \mathbb{F}_p(i)$ 위에서 정의됩니다. 이러한 curve의 $E$의 j-invariant $j(E)$는 $u + vi$꼴입니다 ($u,v \in \mathbb{F}_p$). 각각의 j-invariant가 equivalence class (up to isomorphism) 를 나타내므로 isogney graph의 각 vertex에 대응됩니다. 한편, 이들 중 Supersingular elliptic curve는 $p$-torsion이 Trivial한 경우입니다. $p$-torsion $E[p]$는 $\mathbb{Z}/p\mathbb{Z}$와 isomorphic하거나 trivial함이 알려져 있습니다. 전자의 경우를 ordinary elliptic curve, 후자를 supersingular elliptic curve라 합니다.

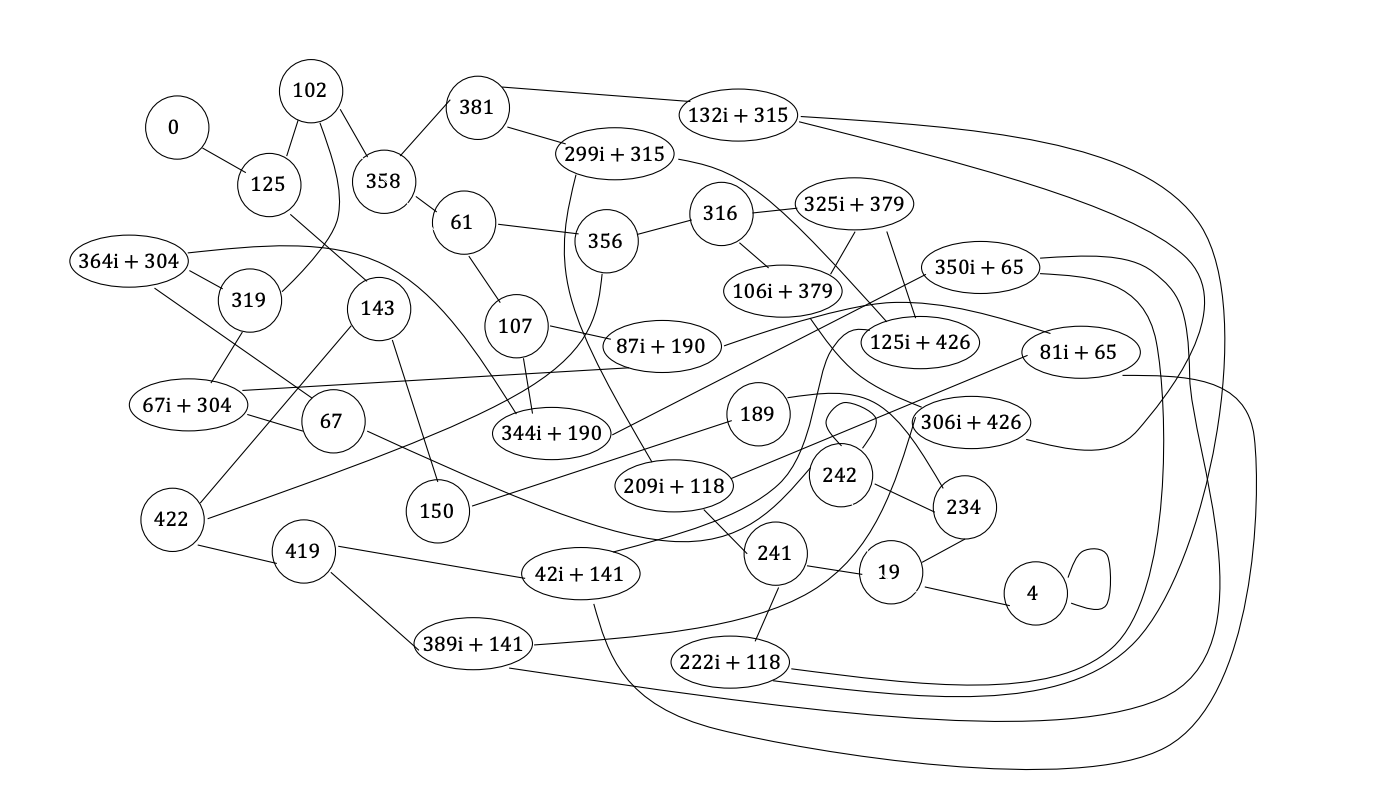
$Supersingular 2-Isogeny graph over $\mathbb{F}_{431^2}$: Craig Costello, 2019$

$\mathbb{F}{p^2}$의 $\ell$-isogeny graph에서, Supersingular elliptic curve에 해당하는 vertex는 하나의 component를 이루게 됩니다. 이를 supersingular $\ell$-isogeny graph라 합니다. 위 그림은 $\mathbb{F}{431^2}$의 supersingular 2-isogeny graph의 각 vertex에 j-invariant를 적어놓은 형태입니다.

그림에서 볼 수 있듯이 supersingular isogeny graph는 거의 모든 vertex가 degree $\ell + 1$을 가지며 랜덤한 성질을 지닙니다. $p=431$인 경우 vertex가 37개인데, $p$가 커져도 vertex의 개수는 $p/12$개 정도를 유지하기 때문에 $p$에 비례하는 크기를 갖게 됩니다. 즉 supersingular isogeny graph는 크기가 exponential하며(p에 비례하면 exponential한 것입니다) 모든 정점에서 비슷한 차수를 가지며 랜덤성을 가지는 그래프로, 위에서 말한 조건을 만족함을 알 수 있습니다.

이제 그래프는 조건을 만족한다는 것을 확인했으니, 이제 Alice와 Bob이 서로 Commutative한 secret path를 efficient하게 계산할 수 있다면 Diffie-Hellman protocol을 만들 수 있습니다. 만약 path의 길이가 짧다면 brute-force attack으로 secret path를 알아내는 공격이 통할 것이고, path가 긴데 한 step씩 계산을 해야 한다면 이는 계산량이 많아 현실적이지 않을 것입니다. $\ell$-isogeny graph에서 여러 edge로 이루어진 Path에 해당하는 composite isogeny를 효율적으로 계산하려면 어떻게 해야 할까요?

SIDH, Revisited

다행히 우리는 임의의 subgroup에 대해 이를 kernel로 하는 isogeny를 생성하는 방법인 Velu’s formula의 존재를 이미 배웠습니다. 그러면 다음과 같이 세팅된 상태를 생각해봅시다.

$p = 2^e3^f-1$, $E:y^2 = x^3+x$ is a supersingular curve over $\mathbb{F}_{p^2}$
$2^e$-torsion $E[2^e] = <P_A, Q_A>$, $3^f$-torsion $E[3^f] = <P_B, Q_B>$

이제 앞서 간단히 살펴본 SIDH의 틀을 적용할 차례입니다. Alice는 $a \in \mathbb{Z}$를 골라 $A = <P_A + aQ_A>$를, Bob은 $b \in \mathbb{Z}$를 골라 $B = <P_B + bQ_B>$를 계산합니다. 이 때 $A \subset E[2^e]$, $B \subset E[3^f]$가 성립하고, $A$를 kernel로 하는 isogeny $\varphi_A: E \rightarrow E/A$는 2-isogeny들의 composition이 됩니다. 즉, supersingular 2-isogeny graph의 walk이 됩니다. 마찬가지로, $\varphi_B$는 3-isogeny graph의 walk이 됩니다. 따라서, $\varphi_A$와 $\varphi_B$에 해당하는 walk은 각각 $a$와 $b$에 따라 달라지는 한편 위 SIDH에서 언급한 것처럼 $E_{AB}$와 $E_{BA}$의 j-invariant는 같아지게 되어 결국 graph에서의 Diffie-Hellman key exchange가 성공적으로 이뤄질 수 있게 됩니다.

Why SIKE(SIDH) were broken?

이때까지 설명한 Supersingular Isogeny Key Exchange(Diffie-Hellman)은 올 7월에 발표된 Castryck-Decru의 방법으로 앞서 본 $p = 2^e3^f-1$꼴과 같은 세팅에서 attack이 가능함이 알려졌고, 8월에는 Damien Robert가 모든 케이스의 SIDH에 attack이 가능한 방법까지 발표하여 결국 완전히 깨지고 말았습니다. 이 공격에 대한 자세한 내용은 필자도 아직 제대로 이해하지 못했기 때문에 몇 가지 자료를 소개하고 마치도록 하겠습니다.