Dilworth's Theorem
Introduction
딜워스의 정리(Dilworth’s Theorem)는 부분 순서 집합(partially ordered set)에서 최대 반사슬(antichain)의 크기는 사슬 분할의 최소 개수와 같다는 정리입니다. 먼저 용어들을 설명하겠습니다.
부분 순서 집합이란 말 그대로 순서가 부분적으로 정의된 집합입니다. 예를 들어 자연수 집합 $S$에서 $x$가 $y$로 나누어 떨어질 때 $x\geq y$로 정의하는 경우 $S$를 부분 순서 집합이라고 생각할 수 있습니다. 여기서 6과 3은 비교 가능하지만 6과 5는 비교 불가능합니다. 다른 예시는 2차원 좌표를 원소로 하는 집합에서 $x_1\leq x_2,y_1\leq y_2$이면 $(x_1,y_1)\leq(x_2,y_2)$로 정의하는 것입니다. 여기서는 (1,5)와 (2,6)은 비교 가능하지만 (1,5)와 (2,3)은 비교 불가능합니다. 일반적으로는 순서관계를 방향이 있는 간선으로 나타낸 방향그래프 DAG를 생각하면 편합니다. DAG에서 $x$에서 $y$로 가는 경로가 존재한다면 $x$와 $y$는 비교 가능한 것입니다. 부분 순서는 추이성( $x\leq y\leq z$라면 $x\leq z$)를 만족해야하므로 그래프에 사이클이 있어서는 안 됩니다.
$<$연산자와 $\leq$연산자 둘 중 하나만 정의되어도 나머지 하나를 유도할 수 있기 때문에 둘 중 하나만 잘 정의되면 부분 순서 집합이라고 할 수 있습니다. 엄밀하게는 다음과 같습니다.
부분 순서 집합 $S$에서 이항관계 $\leq$는 다음 성질들을 만족해야 합니다.
- 임의의 $x \in S$에 대하여 $x\leq x$
- 임의의 $x,y,z \in S$ 에 대하여 $x\leq y\leq z$ 라면 $x \leq z$
- 임의의 $x,y \in S$에 대하여 $x\leq y\leq x$라면 $x=y$
부분 순서 집합 $S$에서 이항관계 $<$는 다음 성질들을 만족해야 합니다.
- 임의의 $x \in S$에 대하여 $x\not\lt x$
- 임의의 $x,y,z \in S$ 에 대하여 $x< y< z$ 라면 $x \lt z$
- 임의의 $x,y \in S$에 대하여 $x\lt y $라면 $x\not\gt y$
부분 순서 집합 $S$의 부분집합 $S’$에서 모든 원소끼리 순서가 정의된다면 $S’$을 사슬(chain)이라고 합니다. 즉 $S’$의 임의의 두 원소 $x,y$에 대하여 $x\lt y$이거나 $x>y$여야 합니다. 반대로, $S’$의 어떠한 두 원소끼리도 순서가 정의되지 않는다면 $S’$을 반사슬(antichain)이라고 합니다. 사슬이 아니라고 해서 반사슬인 것은 아닙니다. 사슬 분할이란 부분 순서 집합 $S$을 모든 원소가 각각 하나의 사슬에 포함되도록 여러 개의 사슬로 분할하는 것입니다. 이 때 사슬 개수의 최솟값이 반사슬의 최대 크기와 같다는 것이 딜워스의 정리입니다.
예를 들어 집합 $S= \lbrace (1,1),(2,3),(3,2),(4,4)\rbrace $를 생각하고 $x_1\leq x_2,y_1\leq y_2$이면 $(x_1,y_1)\leq(x_2,y_2)$로 정의합시다. 여기서 사슬 분할을 $\lbrace(1,1),(2,3)\rbrace,\lbrace(3,2),(4,4)\rbrace$와 같이 할 수 있고 이것보다 적은 개수로 분할할 수는 없습니다. 그리고 반사슬은 $\lbrace(1,1)\rbrace,\lbrace(2,3),(3,2)\rbrace$등이 있고 반사슬의 최대 크기는 2로 사슬분할의 최솟값과 같다는 것을 알 수 있습니다.
Proof
쾨닉의 정리(Kőnig’s Theorem)를 이용한 증명과 수학적 귀납법을 이용한 증명이 있습니다. 쾨닉의 정리를 이용한 증명은 문제풀이에 직접적으로 이용되는 경우가 있기 때문에 잘 알아두는 것이 좋습니다. 귀납법을 이용한 증명은 다소 비직관적이고 어렵기 때문에 여기서 서술하지는 않겠습니다.
쾨닉의 정리를 이용한 증명
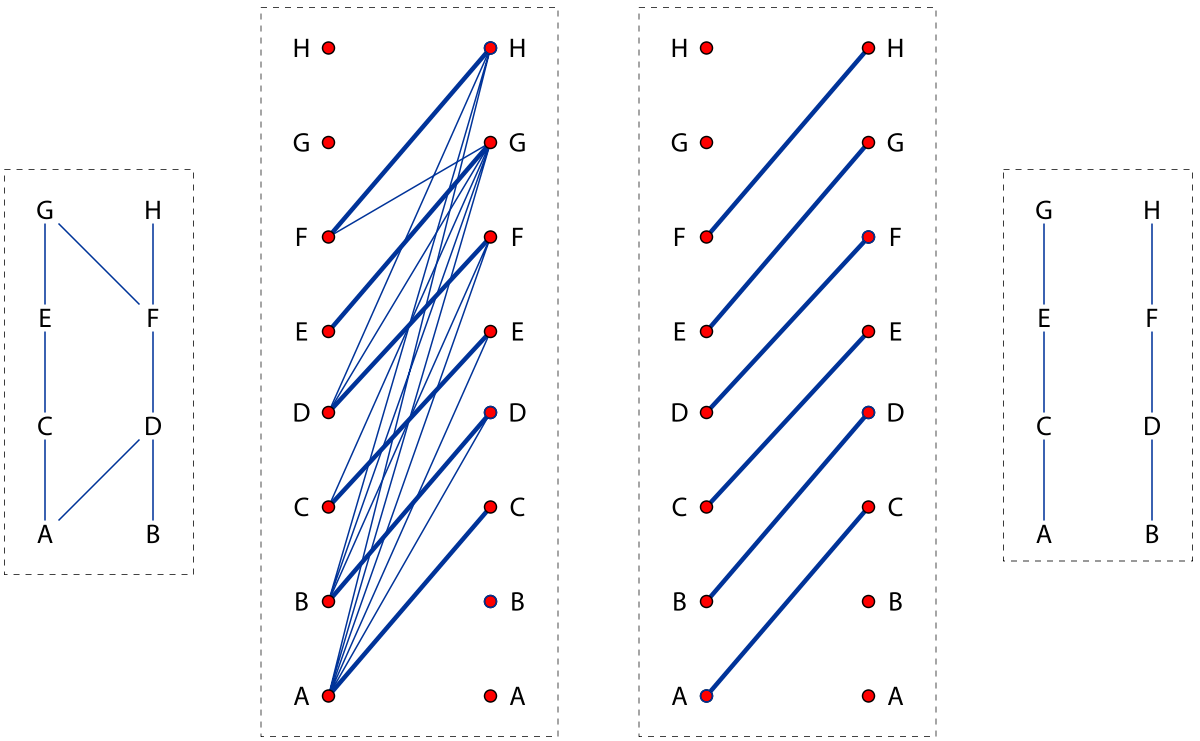
부분 순서 집합을 이용하여 이분그래프를 만듭니다. 부분 순서 집합 $S$에서 $x\lt y$라면 이분그래프의 왼쪽 정점 집합 $L$의 $x$에서 오른쪽 정점 집합 $R$의 $y$로 간선을 만들어 줍니다. $L$은 outdegree, $R$은 indegree를 나타낸다고 생각하면 됩니다. 여기서 매칭을 찾고 그 크기를 $m$이라고 합시다. 이 때 매칭을 재귀적으로 따라가면 사슬이 만들어지며 이 사슬들을 이용해 사슬분할을 할 수 있습니다. 그리고 놀랍게도 사슬들의 개수는 $n-m$이 됩니다. 사슬의 개수는 $L$또는 $R$에서 차수가 0인 정점의 개수(indegree 또는 outdegree가 0인 정점의 개수)와 같기 때문입니다. 그리고 최대매칭일 경우 최소 사슬분할을 얻을 수 있습니다.
이번엔 이분그래프의 버텍스 커버를 생각해봅시다. 버텍스 커버의 여집합의 정점들 사이에는 간선이 존재하지 않기 때문에 버텍스 커버의 여집합은 반사슬을 이룹니다. 쾨닉의 정리에 의해 이분그래프의 최소 버텍스 커버의 크기는 최대 매칭의 크기와 같기 때문에 반사슬의 크기 역시 $n-m$이 됩니다.
Applications
Nested Dolls(NCPC 2007 G번)
$N$개의 인형이 있으며 각 인형은 $w_i$의 너비와 $h_i$의 높이를 가집니다. $w_i< w_j,h_i< h_j$이면 $i$번 인형을 $j$번 인형 안에 넣을 수 있습니다. 이 때 인형들을 다른 인형 안에 넣어 최소 개수의 인형만 남게 하는 것이 문제입니다.
$(w_i,h_i)$가 $(w_j,h_j)$보다 순서가 작다면 $i$번 인형을 $j$번 인형 안에 넣을 수 있습니다. 인형을 다른 인형 안에 넣는 것을 사슬을 연결하는 것으로 볼 수 있습니다. 따라서 문제에서 요구하는 것은 사슬분할의 최소개수입니다. 딜워스의 정리에 의해 이것은 반사슬의 최대 크기와 같습니다. 반사슬의 최대 크기는 $O(N\times \log N)$으로 LIS를 구하는 알고리즘을 이용하면 얻을 수 있습니다.
사실 여기서 이상한 부분이 있습니다. 문제에서 입력되는 인형들의 정보가 서로 다르다는 조건이 없습니다. 집합이 아닌데도 딜워스의 정리를 적용할 수 있을까요? 그렇습니다. 위의 쾨닉의 정리를 이용한 증명을 살펴보면 같은 원소가 여러 개 있더라도 결론에 차이가 없습니다. 따라서 안심하고 딜워스의 정리를 사용하면 됩니다.
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n;
cin>>n;
vector<pair<int,int>> a(n);
for(auto &k: a)cin>>k.first>>k.second;
sort(a.begin(),a.end(),[&](pair<int,int> x,pair<int,int> y){
if(x.first==y.first)return x.second>y.second;
return x.first<y.first;
});
vector<int> v;
for(auto k: a){
int x=upper_bound(v.begin(),v.end(),-k.second)-v.begin();
if(x==v.size())
v.push_back(-k.second);
else
v[x]=-k.second;
}
cout<<v.size()<<"\n";
}
int main(){
cin.tie(0);
ios_base::sync_with_stdio(0);
int T;
cin>>T;
while(T--)solve();
return 0;
}
COW JOG(USACO December 2014 Gold 3번)
앞의 문제와 거의 동일한 문제입니다.
Treasure Hunter(Seoul Nationalwide Internet Competition 2021 K번)
앞의 문제와 거의 동일한 문제입니다.
Algorithm Teaching(Latin America Regional 2019 A번)
$N$명이 선생님이 있습니다. 선생님들은 $A$개의 알고리즘을 가르칠 수 있습니다. 예를 들어 1번 선생님은 BFS,DFS,LCA,RMQ를 가르칠 수 있고 2번 선생님은 BFS,DFS,DIJKSTRA를 가르칠 수 있습니다. 한 학생은 한 명의 선생님에게서만 알고리즘을 배울 수 있습니다. 각 학생들은 배운 알고리즘들이 서로 포함관계가 되어서는 안 됩니다. 예를 들어 어떤 학생이 DFS와 BFS를 배우고 다른 학생이 DFS,BFS와 LCA를 배워서는 안 됩니다. 이 때 알고리즘을 배울 수 있는 학생 수의 최댓값을 구하는 것이 문제입니다.
포함관계는 추이성을 만족하기 때문에 순서관계입니다. 학생들이 배울 수 있는 알고리즘 집합의 개수는 $O(N\times2^A)$입니다. 포함관계를 간선으로 나타낸다면 간선의 개수는 최대 $O(N\times 3^A)$가 됩니다. 이제 이 DAG에서 반사슬의 최대 크기를 구하면 됩니다. 이것은 DAG를 이분그래프로 펼치고 최대 매칭을 구하여 정점의 개수에서 빼주는 것으로 가능합니다. 최대 매칭을 호프크로프트 카프 알고리즘을 이용해 구하면 $O(N^{\frac{3}{2}}\times 3^A\times2^{\frac{A}{2}})$정도의 시간복잡도로 풀 수 있습니다.
사실 이렇게 DAG를 이분그래프로 바꿔서 최대매칭을 통해 사슬분할의 개수를 구하는 기법은 부분 순서 집합뿐만 아니라 일반적인 그래프에서도 최소 경로분할을 구하는 데 이용할 수 있습니다. 예시 문항으로는 BOJ 3295 등이 있습니다.
#include <bits/stdc++.h>
using namespace std;
//호프크로프트 카프 코드 출처: https://blog.naver.com/kks227/220816033373
const int MAXN = 110005, MAXM = 6e6 + 5;
vector<int> gph[MAXN];
int dis[MAXN], l[MAXN], r[MAXM], vis[MAXN];
void clear()
{
for (int i = 0; i < MAXN; i++)
gph[i].clear();
}
void add_edge(int l, int r) { gph[l].push_back(r); }
bool bfs(int n)
{
queue<int> que;
bool ok = 0;
memset(dis, 0, sizeof(dis));
for (int i = 0; i < n; i++)
{
sort(gph[i].begin(), gph[i].end());
gph[i].erase(unique(gph[i].begin(), gph[i].end()), gph[i].end());
if (l[i] == -1 && !dis[i])
{
que.push(i);
dis[i] = 1;
}
}
while (!que.empty())
{
int x = que.front();
que.pop();
for (auto &i : gph[x])
{
if (r[i] == -1)
ok = 1;
else if (!dis[r[i]])
{
dis[r[i]] = dis[x] + 1;
que.push(r[i]);
}
}
}
return ok;
}
bool dfs(int x)
{
if (vis[x])
return 0;
vis[x] = 1;
for (auto &i : gph[x])
{
if (r[i] == -1 || (!vis[r[i]] && dis[r[i]] == dis[x] + 1 && dfs(r[i])))
{
l[x] = i;
r[i] = x;
return 1;
}
}
return 0;
}
int match(int n)
{
memset(l, -1, sizeof(l));
memset(r, -1, sizeof(r));
int ret = 0;
while (bfs(n))
{
memset(vis, 0, sizeof(vis));
for (int i = 0; i < n; i++)
if (l[i] == -1 && dfs(i))
ret++;
}
return ret;
}
bool chk[MAXN + MAXM];
void rdfs(int x, int n)
{
if (chk[x])
return;
chk[x] = 1;
for (auto &i : gph[x])
{
chk[i + n] = 1;
rdfs(r[i], n);
}
}
vector<int> getcover(int n, int m)
{ // solve min. vertex cover
match(n);
memset(chk, 0, sizeof(chk));
for (int i = 0; i < n; i++)
if (l[i] == -1)
rdfs(i, n);
vector<int> v;
for (int i = 0; i < n; i++)
if (!chk[i])
v.push_back(i);
for (int i = n; i < n + m; i++)
if (chk[i])
v.push_back(i);
return v;
}
int main()
{
cin.tie(0);
ios_base::sync_with_stdio(0);
int n;
cin >> n;
vector<vector<int>> a(n);
vector<vector<int>> b;
vector<vector<vector<int>>> v(n);
map<string,int> mp;
int cnt=0;
for (int i = 0; i < n; i++)
{
int m;
cin >> m;
a[i].resize(m);
for (int j = 0; j < m; j++){
string k;
cin>>k;
if(mp[k]){
a[i][j]=mp[k];
}
else{
a[i][j]=mp[k]=++cnt;
}
}
for (int j = 0; j < (1 << m); j++)
{
vector<int> vv;
for (int k = 0; k < m; k++)
{
if ((j >> k) & 1)
vv.push_back(a[i][k]);
}
sort(vv.begin(), vv.end());
v[i].push_back(vv);
b.push_back(vv);
}
}
sort(b.begin(), b.end());
b.erase(unique(b.begin(), b.end()), b.end());
for (int i = 0; i < n; i++)
{
int m = a[i].size();
for (int j = 1; j < (1 << m); j++)
{
int x = lower_bound(b.begin(), b.end(), v[i][j]) - b.begin();
for (int k = (j - 1) & j; k > 0; k = (k - 1) & j)
{
int y = lower_bound(b.begin(), b.end(), v[i][k]) - b.begin();
add_edge(x, y);
}
}
}
int nn = b.size();
cout << nn - match(nn) - 1;
return 0;
}
참고한 글
https://en.wikipedia.org/wiki/Dilworth%27s_theorem https://ko.wikipedia.org/wiki/%EB%B6%80%EB%B6%84%EC%88%9C%EC%84%9C%EC%A7%91%ED%95%A9