A Bayesian Perspective on Federated Learning (1)

Introduction

Federated Learning은 최근에 머신러닝과 인공지능 연구에서 매우 중요한 분야로 떠오르고 있습니다. 이 기술은 분산된 디바이스들의 데이터를 이용하여 중앙 집중식으로 데이터를 수집하지 않고 모델을 학습시키는 것으로, 개인정보 보호와 같은 문제를 해결하는 데 도움이 됩니다.

따라서, Federated Learning은 데이터 프라이버시와 보안 문제가 중요한 분야에서 매우 유용합니다. 이 기술은 인공지능 모델을 개발하는 데 있어서 중요한 문제 중 하나인 데이터 분산 문제를 해결할 수 있습니다. 이러한 이유로, Federated Learning은 최근 많은 관심을 받고 있으며, 새로운 연구와 개발이 계속해서 이루어지고 있습니다.

Federated Learning에서는 local device에 overfitting되는 문제를 해결하기 위해 다양한 방법론이 제시되어왔습니다. 최근에는 Bayesian 방법론이 많은 연구에서 활용되고 있습니다. Bayesian 방법론은 모델의 불확실성을 표현할 수 있어, overfitting을 방지하고 일반화 성능을 향상시킬 수 있습니다.

이러한 Bayesian 방법론을 활용한 Federated Learning 알고리즘 중에서 FedPA라는 알고리즘에 대해 살펴보도록 하겠습니다.

FL as optimization prolem

기존에는 FL이 주로 distributed optimization problem으로 표현되었습니다. client는 local objective를 최소화하고, server에서는 그를 토대로 global objective를 최소화합니다.

global objective function $F(\theta)$는 $N$ 개의 local objective $f_i(\theta)$들의 weighted average입니다. $f(\theta; z) := -\log P(z\|\theta)$ 와 같이 local objective function이 negative log likelihood라면, 이 optimization problem의 solution은 MLE (maximum likelihood estimator)가 됩니다.

global objective
\[\min_{\theta} \{ F(\theta) := \Sigma_{i=1}^N q_i f_i(\theta)\} \tag 1\]
local objective
\[f_i(\theta) := {1 \over n_i} \Sigma_{j=1}^{n_i} f(\theta; z_{ij})\tag 2\]

FedAvg

이러한 문제를 푸는 대표적인 알고리즘에는 FedAvg가 있습니다. FedAvg에 대한 자세한 설명은 kni020님의 글을 참고하시면 도움이 될 것 같습니다.

FedAvg에서는 일반적으로 각 round 마다 수행되는 communication이 bottleneck입니다. communication bottleneck을 해결하기 위해서, 각 round에 client에서 더 많은 local computation (more local SGD steps)을 수행해서 round 수를 줄이고 학습 속도를 높힐 수 있습니다. 하지만 local computation을 많이 수행할수록, client data heterogeneity (non-IID)에 의해 global model이 inferior model로 수렴하는 문제가 발생하게 됩니다. FedPA는 이러한 문제점을 posterior inference를 수행함으로써 해결하고자 합니다.

FL as MAP

위와 같은 MLE 방식의 alternative로, 파라미터들의 posterior distribution을 추론하는 방식이 있습니다.

\[P(\theta\|D \equiv D_1 \cup \cdots \cup D_N) \propto P(D\|\theta) \cdot P(\theta) \tag 3\]

이때 prior $P(\theta)$가 uniform prior이면 (uninformative), modes of the global posterior은 MLE soulutions, 식 (1)의 optima와 일치하게 됩니다.

Posterior Distribution Decomposition

Proposition 1 (Global Posterior Decomposition)

Under the uniform prior, any global posterior distribution that exists decomposes into a product of local posteriors: $P(\theta|D) \propto \Pi_{i=1}^N P(\theta|D_i)$

본 논문에서는 위와 같은 Proposition을 활용하여 global posterior을 local posterior들의 곱으로 decompose 합니다.

간략한 증명은 아래와 같습니다. 다만 uniform prior를 가정한다는 점에서 한계가 있을 것 같습니다.
- Under uniform (uninformative) prior,
- $P(\theta|D) \propto P(D|\theta)$ by Bayesian
- $P(D|\theta) = \Pi_{z \in D} P(z|\theta) = \Pi_{i=1}^N \Pi_{z \in D_i} P(z|\theta)$
- $\Pi_{z \in D_i} P(z|\theta)$ = local likelihood이므로,
- $P(D|\theta) = \Pi_{i=1}^N P(D_i|\theta) \propto \Pi_{i=1}^N P(\theta|D_i)$ by Bayesian
- ⇒ $P(\theta|D) \propto \Pi_{i=1}^N P(\theta|D_i)$

Proposition 1에 따라, local posterior distribution을 각 client에서 추론한 후, server에서 multiplicative averaging을 하면 global posterior를 추론할 수 있게 됩니다.

예를 들어, 차원 d인 linear model로 least squares regression을 하는 상황을 가정하겠습니다.

loss function은 식 (4)와 같습니다.

\[f(\theta; X, y) := {1 \over 2}{||X^T \theta - y_i ||}^2 \tag 4\]

이 경우 client objective는 식 (5)와 같게 됩니다.

\[f_i(\theta; X_i, y_i) := {1 \over 2}{||X_i \theta - y_i ||}^2 \tag 5\]

아래와 같이 $\Sigma^{-1}$과 $\mu_i$를 정의하면,

\[\Sigma_i^{-1} := X_i^T X_i \tag 6\] \[\mu_i := (X_i^T X_i)^{-1} X_i^T y_i \tag 7\]

$f_i(\theta)$는 식 (8)과 같이 쓸 수 있습니다. 식 (8)에 식 (6)과 (7)을 넣어보면 식이 성립함을 쉽게 알 수 있습니다.

\[f_i(\theta) = {1 \over 2} (\theta - \mu_i)^T \Sigma_i^{-1} (\theta - \mu_i) + const \tag 8\]

$f_i(\theta)$를 식 (8)과 같이 쓰면 위 식이 가우시안 분포의 negative log likelihood임을 알 수 있습니다.

$X \sim N(\mu, \Sigma)$인 multivariate gaussian distribution의 pdf는 식 (9)와 같습니다.

\[p(x \| \mu, \Sigma) = {1 \over \sqrt{(2\pi)^d \|\Sigma\|}} exp(-{1 \over 2}(x-\mu)^T \Sigma^{-1} (x-\mu)) \\ where \ \mu \in R^d,\ \Sigma \in R^{d \times d} \tag 9\]

식 (9)에 negative log를 취하면 식 (10)과 같아집니다.

\[-\log(p(x\|\mu, \Sigma)) = {1 \over 2} (x-\mu)^T \Sigma^{-1} (x-\mu) + const \tag{10}\]

따라서 $f_i(\theta)$는 $\theta \sim N(\mu_i, \Sigma_i)$의 negative log likelihood가 되고, $P(\theta|D_i)$는 가우시안 분포가 됩니다.

여기서 앞서 알아본 Global Posterior Decomposition에 따라 uniform prior에서 $P(\theta|D) \propto \Pi_{i=1}^N P(\theta|D_i)$ 가 성립함을 이용할 것입니다.

$P(\theta|D)$ 가 $\theta \sim N(\mu_i, \Sigma_i)$ 들의 곱이라고 할 수 있으므로, $P(\theta|D)$ 또한

\[\Sigma = {1 \over \Sigma_{i=1}^N {1 \over \Sigma_i} \cdot q_i},\ \mu = \Sigma_{i=1}^N {\Sigma \over \Sigma_i} \cdot \mu_i \cdot q_i \tag {11}\] \[\Sigma = {1 \over \Sigma_{i=1}^N {1 \over \Sigma_i} \cdot q_i} = (\Sigma_{i=1}^N \Sigma_i^{-1} q_i)^{-1} \tag {12}\] \[\mu = \Sigma_{i=1}^N {\Sigma \over \Sigma_i} \cdot \mu_i \cdot q_i = \Sigma \cdot (\Sigma_{i=1}^N \Sigma_i^{-1} \mu_i q_i) \tag {13}\]

인 가우시안 분포가 됩니다. ⇒ $P(\theta|D) \sim N(\mu, \Sigma)$

이를 통해 우리가 구하고자 하는 global posterior의 mode (mean) $\mu$는 식 (14)와 같다는 것을 알 수 있습니다.

\[\mu = (\Sigma_{i=1}^N \Sigma_i^{-1} q_i)^{-1} \cdot (\Sigma_{i=1}^N \Sigma_i^{-1} \mu_i q_i) \tag {14}\]

결국 우리는 각 client에서 $\Sigma_i^{-1}$ 와 $\mu_i$ 를 구한 뒤, server에서 식 (14)를 계산하면 global optimum을 구할 수 있게 됩니다.

다만 바로 이 방법을 적용하기에는 문제점이 많습니다.

local posterior distribution을 어떻게 효율적으로 추론할 것인가?
local posterior distribution들을 어떻게 효율적으로 서버에서 aggregation 할 것인가?
local posterior distribution들을 어떻게 효율적으로 서버에 전송할 것인가?

본 논문에서 위 3가지 문제를 어떤 방식으로 해결했는지 알아보겠습니다.

Challenges and Solutions

estimating local means and local covariances

일단 client에서 $\mu_i$와 $\Sigma_i$를 구하기 위해서는 local posterior들을 여러 개 sampling해서 그들의 mean과 covariance를 구하면 됩니다. 그럼 어떻게 local posterior들을 sampling하는지가 중요해집니다.

본 논문에서는 SG-MCMC 방식으로 local posterior들을 sampling 합니다. 저자들은 꼭 이 방식이 아니라 다른 방식으로 sampling해도 된다며, 이 sampling 방식들에 대한 분석은 future work를 남겨준다고 언급하고 있습니다. 사실상 본 논문에서는 local posterior를 sampling하는 방식보다는 global posterior decomposition에 따라 global posterior를 local posterior를 곱으로 구한다는 접근과, 그를 어떻게 구현했는지가 중요한 부분이기 때문에 이에 관한 설명은 간략히만 하고 넘어가겠습니다.

Algorithm 4를 보면 먼저 server에서 전달받은 $\theta$를 client에서 $B$ step 만큼 update 합니다. (Burn-in) 그 후에 $l$ 개의 sample을 sampling할 것인데, $K$ step 동안 update한 $\theta$의 평균이 하나의 sample이 됩니다. 이러한 방식으로 총 $l$ 개의 sample을 뽑아 local posterior를 계산합니다.

using SGD instead of matrix inversion

식 (12)는 $d \times d$ 행렬의 역행렬입니다. 따라서 이를 계산하는데 $O(d^3)$이 필요합니다. 또한 그 계산에 필요한 $\Sigma_i^{-1}$ 들을 각 client가 server에게 전송해야하기 때문에 $O(d^2)$ 의 communication이 필요합니다. 차원 $d$ 가 커진다면 이는 FedAvg에서 사용하는 방식과 같은 SGD에 비해서는 매우 큰 계산량입니다.

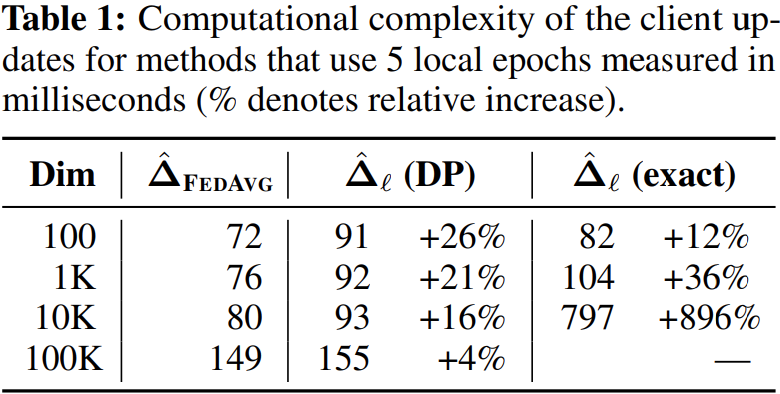
Table 1에서 첫 번째 col이 FedAvg에서의 계산량이며, 세 번째 col이 앞서 설명한 방식의 계산량입니다. 차원이 100으로 작을 때는 12% 정도의 차이가 나지만, 차원이 1만 정도만 되더라고 896% 정도로 매우 큰 차이가 납니다. 따라서 이 방식을 실제로 사용하기는 어려우며, 계산량을 SGD와 유사할 정도로 줄여야 합니다.

본 논문에서는 계산량을 줄이기 위해서 SGD와 유사하게 optimization problem의 optimum으로 $\mu$ 를 구하는 방식을 사용했습니다.

\[Q(\theta) := {1 \over 2} \theta^T A \theta - b^T \theta \\where \ A:= \Sigma_{i=1}^N q_i \Sigma_i^{-1},\ b:=\Sigma_{i=1}^N q_i \Sigma_i^{-1} \mu_i \tag {15}\]

식 (15)와 같이 quadratic objective를 설정해봅시다. 이를 미분하면,

\[\triangledown Q(\theta) = A \theta - b \tag {16}\]

이 됩니다. 그럼 $\triangledown Q(\theta^) = 0$ 인 $\theta^$ 에 대해서 식 (18)을 만족합니다.

\[A \theta^* - b =0 \Rightarrow \theta^* = A^{-1} b \tag {17}\] \[\theta^* = (\Sigma_{i=1}^N q_i \Sigma_i^{-1})^{-1} \cdot (\Sigma_{i=1}^N q_i \Sigma_i^{-1} \mu_i) = \mu\tag {18}\]

따라서 $Q(\theta)$ 의 minimizer가 global posterior의 mean인 $\mu$ 가 됩니다.

이 방식을 이용해서 우리는 $O(d^3)$의 상당한 계산량이 드는 matrix inversion 대신, $Q(\theta)$ 의 minimizer를 구하여 계산량을 줄일 수 있습니다.

식 (16)을 풀어보면 아래와 같습니다.

\[\triangledown Q(\theta) = A\theta - b \\ = (\Sigma_{i=1}^N q_i \Sigma_i^{-1})\theta - (\Sigma_{i=1}^N q_i \Sigma_i^{-1} \mu_i) \\ = \Sigma_{i=1}^N q_i \Sigma_i^{-1}(\theta - \mu_i) \tag {19}\]

여기서 $\Sigma_i^{-1}(\theta - \mu_i)$ 를 $\Delta_i$로 정의하면 ($\Delta_i := \Sigma_i^{-1}(\theta - \mu_i)$),

server에서 아래와 같이 server update를 수행하여 $\theta^*$ 를 찾을 수 있습니다.

\[\theta_{t+1} = \theta_{t} - \alpha[\triangledown Q(\theta_t)] \\ = \theta_{t} - \alpha[A\theta_t - b] \\ = \theta_{t} - \alpha[\Sigma_{i=1}^N q_i \Delta_{i, t}] \tag {20}\]

그럼 client에서 $\Delta_{i, t}$ 를 계산한 후 server로 보내고, server는 client들로 부터 받은 $\Delta_{i, t}$ 를 이용해서 $\triangledown Q(\theta_t)$를 계산하고, 다시 $\theta_{t+1}$ 을 update하기만 하면 될까요?

그렇지 않습니다. $\Delta_{i, t}$ 를 server로 보내는 것은 $O(d)$로 충분히 작습니다. 하지만 $\Delta_{i, t}$ 를 계산하기 위해서 결국 $\Sigma_i^{-1}$를 계산해야 하는데, $\Sigma_i$ 가 $d \times d$ 행렬이므로 역행렬 계산에 $O(d^3)$의 계산량이 필요합니다.

결국 communication 시간을 $O(d^2)$에서 $O(d)$로 단축시켰지만, 계산량은 여전히 $O(d^3)$으로 상당히 큽니다.

using shinkage estimator

본 논문에서는 $\Delta_{i, t}$ 를 빠르게 계산하기 위해 shrinkage estimator를 사용합니다.

Theorem 3

Given approximate posterior samples ${\hatθ_1, \cdots, \hatθ_l}$, let $\hat\mu_l$ be the sample mean, $\hat S_l$ be the sample covariance, and $\hat \Sigma_l := \rho_l I + (1 - \rho_l) \hat S_l$ be a shrinkage estimator of the covariance with $\rho_l := 1/(1+(l-1)\rho)$ for some $\rho \in [0, +\infty)$. Then, for any $\theta$, we can compute $\hat \Delta_l = \hat \Sigma_l^{-1} (\theta - \hat \mu_l)$ in $O(l^2d)$ time and using $O(ld)$ memory.

Theorem 3에 의해서 shringage estimator를 사용하면 DP 알고리즘을 이용하여 $\hat \Delta_l$ 을 $O(l^2d)$만에 구할 수 있습니다. 논문의 본문과 Appendix C에 증명이 있으니 증명이 궁금하신 분들은 논문을 참고해주시길 바랍니다. 본 글에서는 증명은 생략하도록 하겠습니다.

Table 1을 다시 보시면 두 번째 col이 이 방식을 사용했을 때의 계산량을 나타낸 것입니다. FedAvg와 비교할 때 계산량이 크게 차이가 나지 않는 것을 볼 수 있습니다. 또한 차원이 커질수록 더욱 그 차이가 줄어들어 계산량이 거의 유사합니다.

여기까지의 내용을 정리하자면 아래와 같습니다.

client에서 $\hat \Delta_{i,t} = \hat \Sigma_{i,t}^{-1} (\theta_t - \hat \mu_{i,t})$ 를 $O(l^2d)$만에 계산
client에서 $O(d)$만에 $\hat \Delta_{i,t}$ 를 server로 전송
server에서 $\theta_{t+1} = \theta_{t} - \alpha[\Sigma_{i=1}^N q_i \hat \Delta_{i, t}]$ 의 server update를 수행
위 과정을 반복하여 $\theta^* (= \mu)$ 를 구함

FedAvg vs FedPA

FedPA을 간단히 요약하면 approximately하게 global posterior의 mean을 여러 communication rounds에 걸쳐 update하면서 계산하는 알고리즘입니다.

FedPA가 상당히 복잡하게 유도되었지만, 사실상 FedPA는 Algorithm 1에서 Client update 함수만 변경된 FedAvg의 variant입니다. FedPA의 관점에서 보면, FedAvg는 $\hat \Sigma$를 $I$로 estimate한 FedPA라고 볼 수도 있습니다 ($\hat \Delta_{FedAvg} := I(\theta - \hat \mu)$). 본 논문에서와 같이 $\Sigma$를 구하지 않아도 되기 때문에 FedPA와 같이 복잡한 과정이 필요없었던 것입니다. 반대로 FedPA에서는 $\Sigma$를 고려하기 위해 앞서 우리가 살펴본 복잡한 과정을 거쳤던 것입니다. FedAvg에서는 이처럼 client들 간의 covariance를 무시했기 때문에 bias-variance trade-off에 따라 FedPA보다는 더 biased, 즉 overfitting되는 경향이 있습니다.

Figure 1을 보시면, FedAvg에서는 client가 biased (overfitting)되기 때문에 suboptimal point에 수렴합니다. 그에 반해 FedPA는 FedAvg 보다 빠르게, 더 좋은 optimum에 수렴합니다. 또한 FedPA가 수렴할수록, bias-variance trade-off에 따라 bias를 얻으면서 variance가 발생하는 것도 확인하실 수 있습니다.

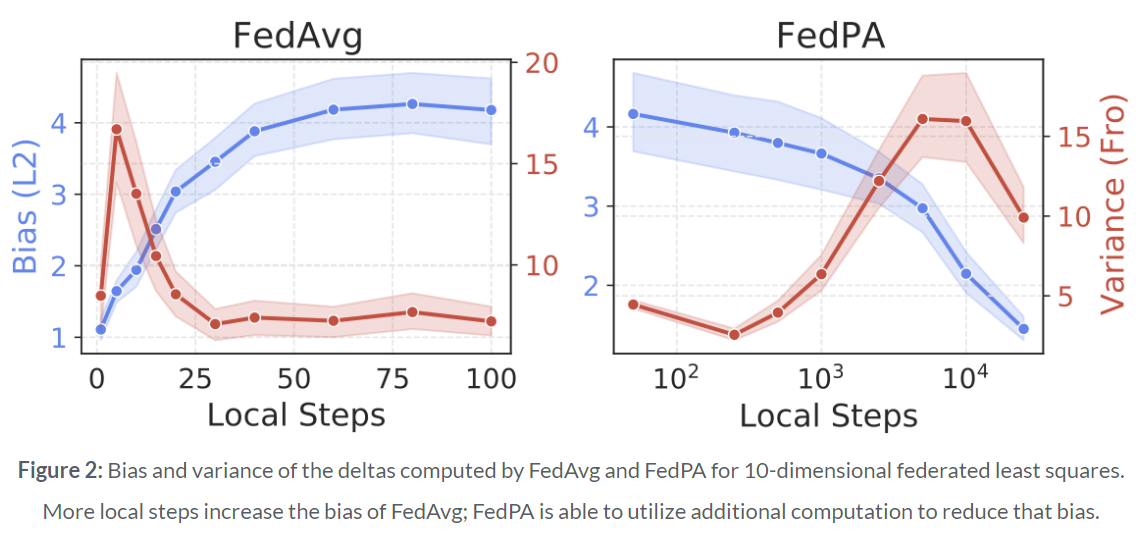
Figure 2는 각 round에 SGD step을 얼마나 수행하는가에 따른 bias와 variance를 비교하고 있습니다. 한 round에 더 많은 local SGD step을 수행하는 경우 FedAvg의 bias가 증가합니다. 이는 model이 overfitting되어서 optimum으로부터 멀리 떨어진 지점에 수렴하도록 합니다. 따라서 FedAvg에서는 global round 수를 줄여 학습 속도를 향상시키기 위해 local SGD step을 늘리는 데 한계가 있습니다. 그에 반해 FedPA에서는 더 많은 local SGD step을 수행할수록 더 많은 posterior sample들을 sampling하게 되고, 이는 local mean과 covariance를 더 잘 예측하도록 합니다. 따라서 model의 bias가 감소하게 되고 FedAvg에 비해서 더 많은 local SGD step을 진행함으로써 더 좋은 optimum으로 수렴할 수 있습니다.

Experiments

본 논문에서는 EMNIST-62, CIFAR-100 dataset에 대한 multi-class image classification task, StackOverflow dataset에 대한 next-word prediction과 tag prediction (multi-label classification task)에서의 FedAvg와 FedPA의 성능을 비교하였습니다. 실험 환경은 Table 2와 같습니다.

이 글에서는 multi-class image classification task에 대한 성능 비교를 중점으로 두고 분석해보겠습니다. StackOverflow dataset에 대한 양상도 유사합니다.

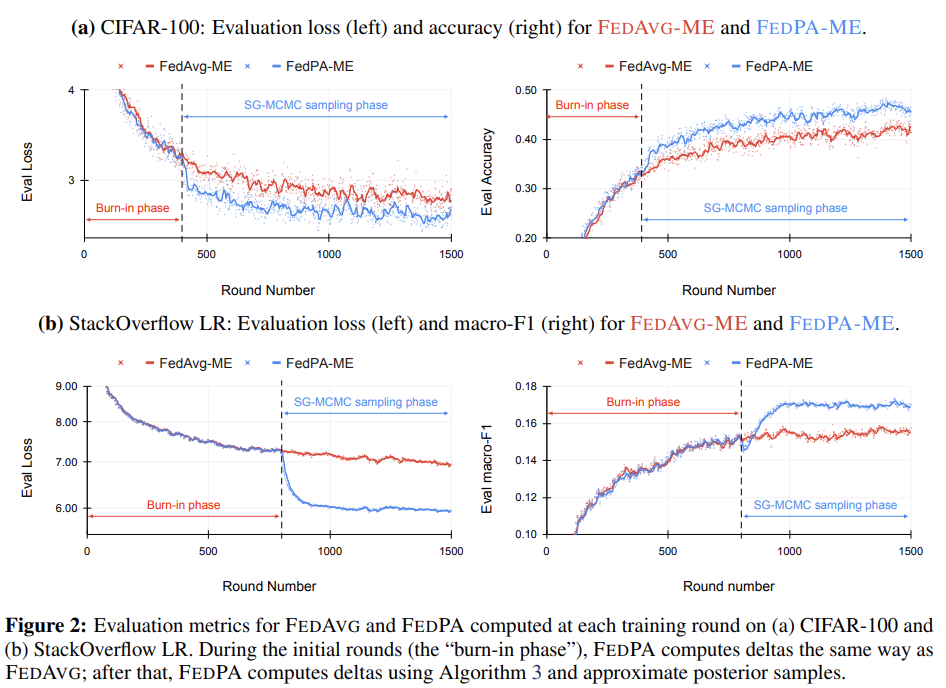
Burn-in phase에서는 FedAvg와 FedPA가 동일 합니다. SG-MCMC sampling을 사용하여 covariance를 고려하는 직후 FedPA가 더 좋은 optimum으로 수렴하는 것을 확인할 수 있습니다.

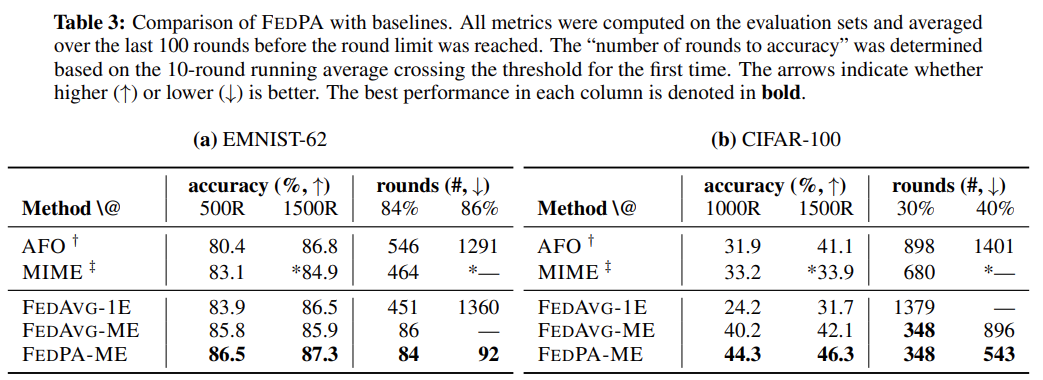
본 논문에서는 2가지의 metric으로 성능을 평가합니다.

첫 번째로는 주어진 rounds 하에서 달성한 최대 accuracy입니다. EMNIST-62 dataset에 대해서는 500 rounds, 1000 rounds를 기준으로 했고, CIFAR-100 dataset에 대해서는 1000 rounds, 1500 rounds를 기준으로 했습니다. Table 3을 보시면 모든 경우에서 FedPA가 FedAvg보다 높은 accuracy를 달성했음을 확인할 수 있습니다.

두 번째로는 주어진 accuracy를 얼마나 빨리 달성하는지를 metric으로 사용합니다. EMNIST-62 dataset에 대해서는 84%, 87%를 기준으로 했고, CIFAR-100 dataset에 대해서는 30%, 40%를 기준으로 했습니다. Table 3을 보시면 모든 경우에서 FedAvg가 더 빠르게 기준 accuracy를 달성했음을 확인할 수 있습니다.

Conclusion

본 논문에서는 FL을 probabilistic inference problem으로 볼 수 있다는 관점을 제시했으며, FedAvg 또한 이러한 접근 방식의 하나로 해석될 수 있음을 보여주었습니다. 본 논문에서는 local posterior들을 sampling하는 방식이나 더 효율적으로 covariance를 계산하는 방법, differential privacy와의 연관성 등 아직 개선하거나 연구할 분야가 많다는 것을 언급합니다. posterior를 decomposition하여 계산하는 접근은 FL에서는 물론, 다른 분야에서도 활용될 수 있는 가능성이 많은 것 같습니다.