Diversified Late Acceptance Search
서론
지역 검색(Local Search) 알고리즘은, 여러 종류의 최적화 문제를 광범위하게 해결하는 데에 사용하고, 다양한 알고리즘의 기준선(baseline)이 될 수 있습니다. 우리는 이 알고리즘 중 기초적인 언덕 오르기(Hill Climbing) 알고리즘과, 그 변형인 늦게 수용하는 언덕오르기(Late Acceptance Hill Climbing, LAHC) 알고리즘 중 하나인 다양성을 갖춘 늦게 수용하는 탐색(Diversified Late Acceptance Search, DLAS)에 대해 알아봅니다.
언덕 오르기 알고리즘과 변형
언덕 오르기 알고리즘은 최적화 문제를 해결하기 위한 간단하고 직관적인 알고리즘 중 하나입니다. 이 알고리즘은 현재 상태에서 지역 최적해를 찾는 데 집중합니다. 즉, 현재 상태에서 근처의 상태들 중 가장 좋은 상태로 이동하면서 최적해를 찾는 방식입니다.
언덕 오르기 알고리즘은 다음과 같은 단계로 구성됩니다.
- 초기 해를 선택합니다.
- 현재 해의 이웃해를 생성합니다.
- 이웃해 중에서 가장 좋은 해를 선택합니다.
- 이웃해가 현재 해보다 더 좋으면 그 이웃해로 이동합니다. 그렇지 않으면 알고리즘을 종료합니다.
이 알고리즘은 간단하고 직관적이지만, 지역 최적해(Local Optimum)에 매우 쉽게 빠진다는 단점이 있습니다. 알고리즘이 여러 번 실행되거나 다른 최적화 알고리즘과 결합하여 사용할 수 있습니다. 이렇기에, 언덕 오르기 알고리즘의 성능을 향상시키기 위해 여러 변형이 제안되었습니다. 이웃해를 선택하고, 좋은 해를 선택하는 것은 맞지만, 좋지 않은 해도 부분적으로 수용하는 방법을 사용하게 됩니다.
아래서 좋은 해란, 어떤 해 S를 평가한 값 F가 낮으면 낮을 수록 좋은 해라고 하겠습니다.
담금질 기법 (SA)
이 변형 중 하나는 담금질 기법(Simulated Annealing, SA)입니다. VennTum님의 Exploring Simulated Annealing for Derivative-free Optimization (1) (2) 게시글에 잘 작성이 되어있습니다. 기본적으로 금속학의 담금질에서 아이디어를 가져온 SA는 물질을 천천히 냉각하여 저에너지 결정상태에 도달하는 과정을 모방합니다. 담금질 기법은 높은 온도에서 시작하여 광범위한 해공간을 탐색할 수 있도록 하고, 그 이후에 점차적으로 온도를 낮추어 전역 최적해(Global Optimum)로 수렴하게 만듭니다.
늦게 수용하는 언덕 오르기 (LAHC)
다른 방법은 늦게 수용하는 언덕오르기(Late Acceptance Hill Climbing, LAHC)입니다. 이는 최근에 본 해를 추가적으로 수용하는 늦은 수용 기준(late acceptance criterion)을 사용합니다. LAHC는 최근 과거에서 본 최고의 해를 유지하고, 새로운 해를 현재 최적해보다 얼마나 더 나쁜지, 혹은 언제 봤는지에 따라 일정한 확률로 수용합니다.
유사코드는 다음과 같습니다. 이 코드는 해의 크기로 초인자(hyperparameter) L을 받습니다. 종료 조건은 정해진 몇 단계, 혹은 몇 반복동안 새로운 지역해를 못 찾았을 경우 등으로 사용할 수 있습니다.
function LAHC:
랜덤으로 해 S와 평가치 F를 만든다.
P <- 길이 L의 [F, F, ..., F] 배열
k, S_min, F_min <- 0, S, F
while 종료 조건:
S', F', l <- S의 랜덤한 이웃, S'의 평가치, k mod L
if F' <= F or F' < P[l]:
S, F <- S', F' # 해를 선택합니다.
if F < F_min:
S_min, F_min <- S, F # 최적해를 갱신합니다.
P[l] <- min(F, P[l])
k <- k + 1
return S_min
이 알고리즘의 경우에는, 여러개의 해를 동시에 탐색한다고 볼 수도 있습니다. L번 단위로 언덕 오르기 알고리즘을 사용한다고 볼 수 있습니다.
이제, LAHC의 변형이라고도 볼 수 있는, 간단하면서 동시에 매우 성능이 좋은 다양성을 갖춘 늦게 수용하는 탐색(Diversified Late Acceptance Search, DLAS)에 대해서도 알아봅시다.
다양성을 갖춘 늦게 수용하는 탐색 (DLAS)
우선, DLAS의 유사코드 먼저 살펴봅시다.
function DLAS
랜덤으로 해 S와 평가치 F를 만든다.
P <- 길이 L의 [F, F, ..., F] 배열
k, S_min, F_min <- 0, S, F
while 종료 조건:
F_prev <- F
S', F', l <- S의 랜덤한 이웃, S'의 평가치, k mod L
if F' = F or F' < max(P):
S, F <- S', F' # 해를 선택합니다.
if F < F_min:
S_min, F_min <- S, F # 최적해를 갱신합니다.
if (F > P[l]) or (F < P[l] and F < F_prev):
P[l] <- F
k <- k + 1
return S_min
DLAS는 다음과 같은 수용 전략(해를 선택)과 대체 전략(해를 갱신)을 가집니다:
- 수용 전략
- 이전 L개의 최댓값보다 더 작을 때, 혹은 이전과 평가치가 같을 때 해를 수용합니다.
- 해를 탐색할 수 있는 공간을 매우 넓힙니다.
- 대체 전략
- 이전 해인 P[l]이 현재 값인 F보다 작을 경우, 항상 P[l]을 증가시킵니다.
- 이 전략은 더 나쁜 이웃해로 가는 것을 항상 수용하기 때문에, 지역 최적해를 찾는데에 좋은 전략이 아닙니다. 하지만 이렇게 다양성이 늘어남으로써, 전역 최적해를 찾기 더 쉬워집니다.
- F가 P[l]보다 작을 경우, 이전 해보다 더 좋은 해인 경우에만 P[l]을 감소시킵니다.
- 이 방법을 사용하면 지역 최적해나 평원(plateau, 어떤 알고리즘에서 최적해에 도달했지만 그 근처에서 계속해서 같은 해를 반환하는 지역 최적해)에 있을 경우 P[l]을 갱신하는 것을 막습니다.
- 이전 해인 P[l]이 현재 값인 F보다 작을 경우, 항상 P[l]을 증가시킵니다.
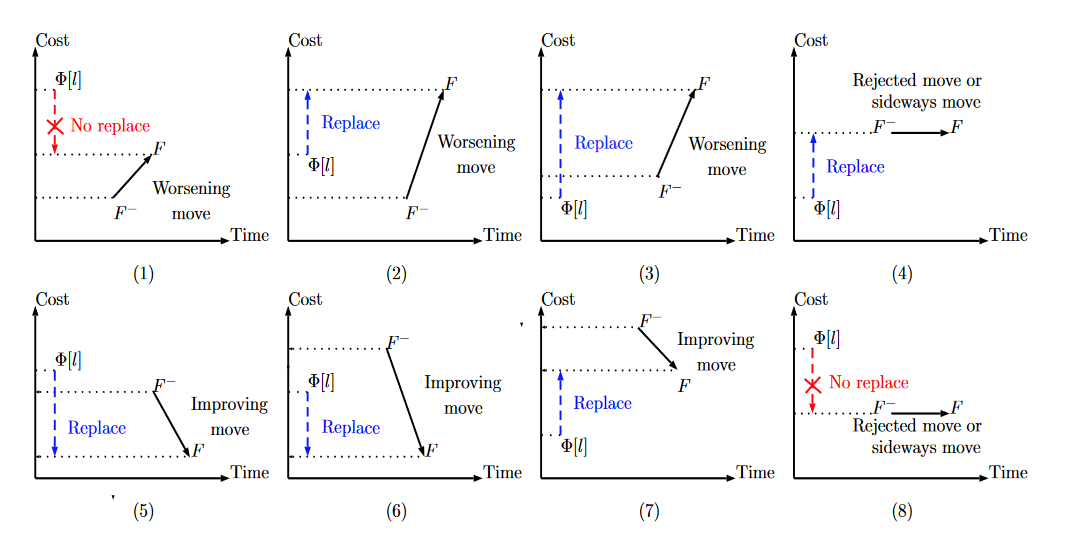
이 방법을 사용할 경우, 기존 SA나 LAHC보다 많은 경우에 더 좋은 최적해를 찾는다는 것이 실험으로 보여졌습니다.
구현
cgiosy님이 구현한 dlas.hpp를 참고하시면, 간단한 f 와 mutate만 작성하는 것으로 우수한 최적해를 찾을 수 있습니다.