SOAP: Schedule Ordered by Age-based Priority
Introduction
Scheduling Policies
우리는 흔히 일상 생활에서 효율적인 일처리를 위해 todo list를 만들거나 시간 단위로 스케줄을 나누어 계획을 세우곤 합니다. 또한, 컴퓨터의 CPU는 여러 개의 처리해야 할 task이 있을 때 어떤 일부터 처리해야 할지 정하고 task를 수행합니다. 이 때 어떤 일부터 처리할지를 잘못 결정한다면 특정 일은 처리하는 시간이 너무 늦어지는 현상이 발생합니다. 이에 대한 결과로 과제를 늦게 제출하거나, 컴퓨터 화면이 멈춰버리는 등의 불상사가 발생하곤 합니다.
처리하는 주체를 server, 처리되어야 하는 일을 job, job들의 대기열을 queue이라고 부르며, server가 어떤 순서로 job을 처리할 지 정하는 방식을 scheduling policy라 합니다.
scheduling policy는 크게 preemptive와 non-preemptive scheduling으로 나눌 수 있습니다. 만약 어떤 job을 처리하던 도중 다른 job을 처리해야 하는 경우가 발생하는 scheduling policy의 경우 preemptive scheduling, 그렇지 않은 경우 non-preemptive scheduling이라 합니다.
대표적인 scheduling policy로는 다음과 같은 방법들이 있습니다.
- first-come, first-served(FCFS): 일찍 들어온 작업부터 먼저 처리하는 방식입니다. 대표적인 non-preemptive scheduling입니다.
- class-based priority: 각 job마다 속하는 class가 있으며, 가장 높은 priority의 class부터 처리합니다. preemptive scheduling으로 구현할 수도 있고, non-preemptive하게 구현할 수도 있습니다.
- shortest job first(SJF): job을 처리하는 데 걸리는 전체 시간이 가장 작은 job부터 처리합니다(non-preemptive: SJF, preemptive: PSJF).
- shortest remaining processing time(SRPT): job을 처리하는 데 앞으로 걸리는 remaining time이 가장 작은 job부터 처리합니다(preemptive).
여러 scheduling policy 중 어떤 policy를 선택하는지에 따라 job들이 queue에 들어갈 때부터 완료될 때 까지 걸리는 시간(response time)은 크게 달라질 수 있습니다. 이에 job들이 최대한 빠르게 처리될 수 있는 policy를 고르는 것은 굉장히 중요합니다. 어떤 policy를 골라야 하는지는 다음과 같은 변수에 따라 크게 달라질 수 있습니다.
- server의 개수: 여러 core가 있는 CPU는 여러 작업을 동시에 수행할 수 있으므로 server 1개인 경우에 비해 scheduling이 상당히 복잡해질 수 있습니다.
- job의 distribution: 각 job을 수행하는 데 걸리는 시간의 distribution, 그리고 job들이 들어오는 rate가 영향을 미칩니다.
- 최적화하고자 하는 대상: job들의 평균적인 response time을 minimize하는 것이 목표일 수도 있고, 안정적인 처리를 위해 maximum response time을 최소로 하고자 할 수도 있습니다.
- 각 job의 처리 시간을 알 수 있는지 여부: 예를 들어, 만약 job이 들어올 때 처리하는 데 걸리는 시간을 알 수 없다면 SRPT policy를 구현할 수 없습니다.
- preemptiveness: practical use case에서는 처리하던 job을 바꿀 수 있는 시간이 정해져 있는 paritally preemptive scheduling인 경우가 많습니다. 실제 cpu의 경우 context switching overhead가 존재하는 것을 예로 들 수 있습니다.
M/G/1 Queue
앞으로 우리가 고려할 문제는 M/G/1 Queue라는 모델로 한정합니다. M/G/1 Queue는 다음과 같은 특성을 가집니다:
- job arrival이 Markovian입니다. 즉, job의 arrival은 Poisson process입니다.
- job의 size(처리하는데 걸리는 시간)은 General한 확률 분포를 따릅니다. 즉, random variable $X$로 생각할 수 있습니다.
- server는 1개입니다.
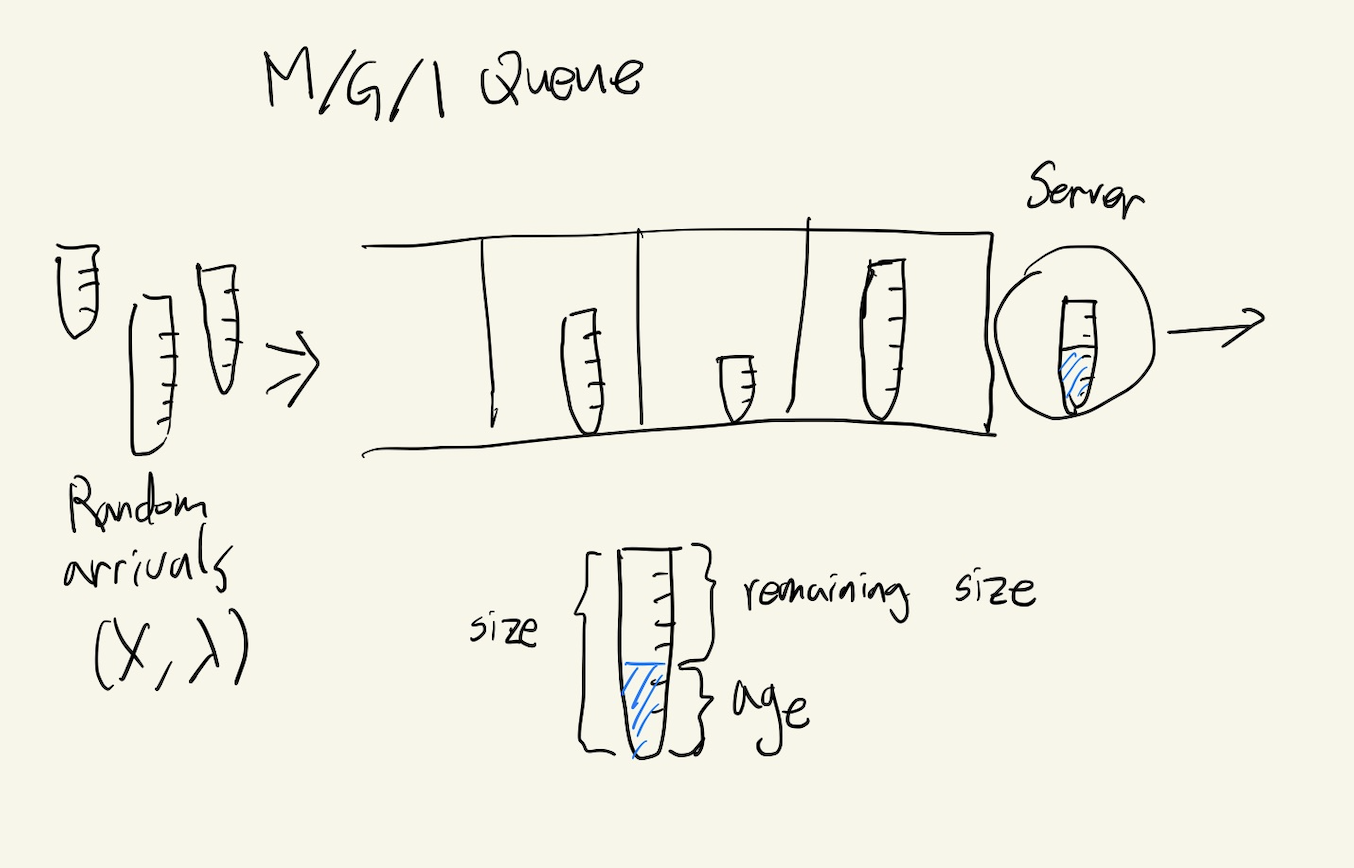
Figure 1. M/G/1 Queue Model
위는 M/G/1 Queue Model을 나타낸 그림입니다.
Poisson process이므로, Arrival rate라 부르는 상수 $\lambda$가 존재하여 $t$만큼의 시간동안 들어오는 job의 개수는 $Poisson(\lambda t)$의 분포를 따릅니다. 그리고 앞서 말한 것처럼, job의 size $X$는 일반적인 random variable로 생각할 수 있습니다. 이 system은 stable하다고 가정합니다. 즉 job이 언젠가 종료됨을 보장하기 위해서 $\lambda E[X] < 1$임을 가정합니다.
각 job들은 완료하는데 size만큼의 시간을 필요로 하고, 해당 job을 이미 처리한 시간을 age, 처리하는데 남은 시간을 remaining size라 합니다.
또한 우리의 일차적 목표는 다음과 같습니다:
- 주어진 Policy의 mean response time $E[T]$에 대한 analysis
Descriptors
Scheduling algorithm에서 사용하는 정보는 static information과 dynamic information으로 나눌 수 있습니다.
Static information이란 job이 들어올 때 주어지는 정보이며 변하지 않는 특성을 가집니다. 여러 class를 갖는 시스템의 경우 job의 class가 static information이 될 수 있습니다. job이 들어올 때 size를 알 수 있는 경우 size가 static information이 될 것입니다. 앞으로 job의 static information을 descriptor라고 부를 것이며, job의 descriptor $d$가 주어졌을 때 size distribtuion을 $X_d$라 부르기로 합니다.
Dynamic information은 job이 queue에 들어오고 server에서 수행됨에 따라 변할 수 있는 정보를 말합니다. 오늘 다룰 scheduling algorithm에서는 age만이 유일하게 사용될 것입니다.
앞서 말한 목표에 해당하는 mean response time은 descriptor마다 기댓값이 다를 것이므로, 우리의 목표는 다음과 같이 다시 쓸 수 있습니다: descriptor $d$에 대한 mean response time $E[T_d]$ 구하기
SOAP scheduling Policy
SOAP scheduling policy는 다음과 같습니다.
- SOAP scheduling policy is a preemptive priority policy where a job’s descriptor and age determine its priority.
즉, SOAP scheduling policy에서 어느 시점에 어떤 job이 처리될지는 남아있는 job들의 descriptor와 age의 함수인 priority에 의해 결정됩니다. 이 때 tie-breaking rule은 FCFS입니다.
이를 다음과 같이 rank function으로 정의하면 보다 다루기 편리합니다:
- a set $\mathcal{R}$ of ranks
- strict total order < on $\mathcal{R}$
- rank function $r(d,a) \rightarrow \mathcal{R}$ ($d$: descriptor, $a$: age)
- 어느 시점이든지, minimum rank의 job을 serve (tie-breaking rule: FCFS)
앞으로 다룰 SOAP policy들에서 rank들의 set $\mathcal{R}$은 주로 $\mathbb{R}$이거나 $\mathbb{R} \times \mathbb{R}$입니다. 이를 각각 실수 $r$이나 순서쌍 $<r1, r2>$로 표현할 것입니다.
Examples of SOAP policies
-
FCFS policy는 SOAP policy입니다. 기본적인 tie-breaking policy가 FCFS이기 때문에, rank function $r = c$ ($c$는 상수)로 정의되는 policy는 FCFS policy 입니다. $r(a) = -a$ 와 같이 정의하면 age가 커짐에 따라 rank가 계속 감소하므로 수행하는 도중 job이 바뀌는 일이 없어 이 역시 FCFS policy가 됩니다. 이와 같이 여러 rank function이 FCFS policy에 대응될 수 있습니다.
-
non-preemptive SJF는 job의 size $x$를 static information으로 갖습니다. $r(x,a)= <-a, x>$로 정의하면 SJF scheduling이 됨을 확인할 수 있습니다. 이처럼 non-preemptive policy는 $<-a, r_2(x,a)>$ 꼴의 rank function으로 표현할 수 있습니다.
-
preemptive SJF (PSJF)는 $r(x,a) = x$의 rank function을 갖습니다.
-
SPRT는 job의 size $x$를 static information으로 갖습니다. remaining time은 $x-a$이므로, rank function $r(x,a)=x-a$로 정의하면 SPRT policy가 됨을 확인할 수 있습니다.
만약 size $x$가 static information으로 주어질 수 없는 경우는 어떤 Policy들이 있을 수 있을까요? SJF, PSJF, SPRT에서 size와 remaining time을 각각 기댓값으로 치환한 policy를 각각 shortest expected processing time(SEPT), preemptive shortest expected processing time(PSEPT), shortest expected remaining processing time(SERPT)라고 합니다. size 대신 expected size를 사용한다는 점만 다르고 모두 동일합니다.
- SEPT는 rank function $r(d,a) = <-a, E[X_d]>$를 갖습니다.
- PSEPT는 rank function $r(d,a) = E[X_d]$를 갖습니다.
- SERPT는 rank function $r(d,a) = E[X_d-a \mid X_d > a]$를 갖습니다.
rank function에 대한 감을 잡기 위해 예를 들어 보겠습니다. $X$가 $\frac{1}{2}$의 확률로 $2$ 또는 $14$의 값을 가지는 random variable이고, descriptor는 모든 job에 대해 $\phi$로 동일한 경우를 생각해 봅시다. 그러면 age에 따른 SERPT의 rank function은 다음과 같은 그래프로 표현됩니다:
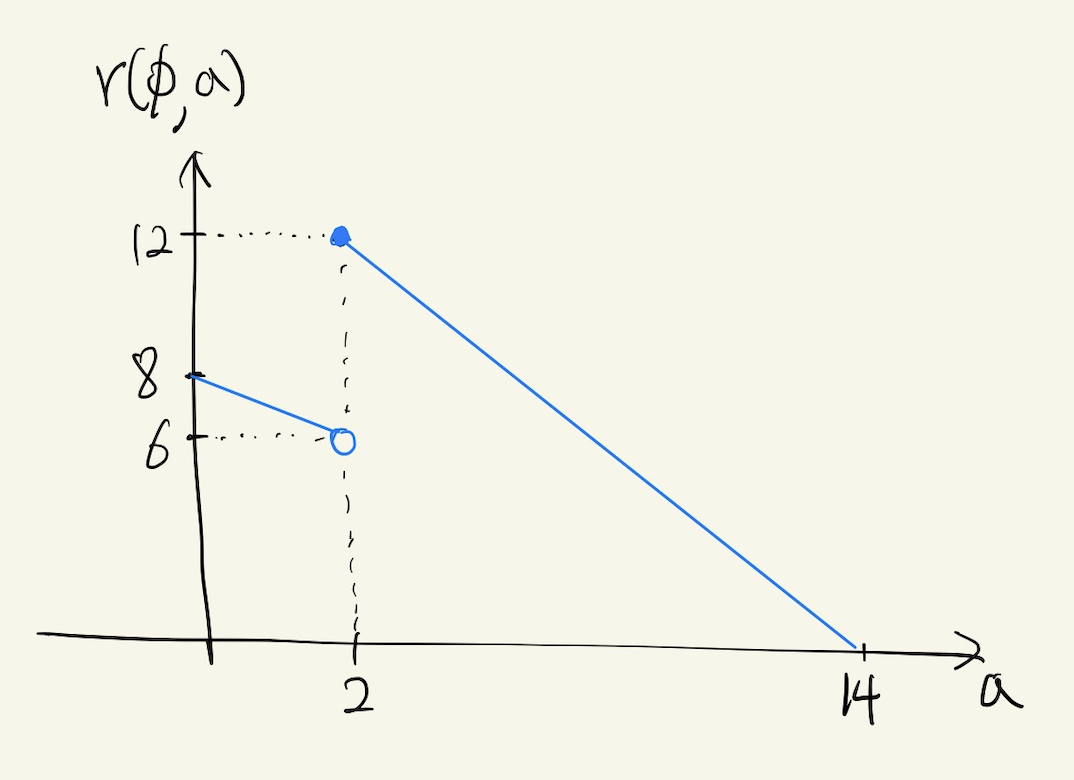
Figure 2. Rank Function for SERPT
$a = 0$일 때는 $E[X_d] = 2 \times \frac{1}{2} + 14 \times \frac{1}{2} = 8$이고, $a$가 증가함에 따라 $r(d,a) = E[X_d-a \mid X_d > a]$가 기울기 1로 감소하다가 $a$가 2 이상이 되면 $X_d > 2$가 보장되므로 $X_d = 14$로 결정이 되어 $r(d,a) = 14 - a$가 됩니다.
일정 주기로만 job을 바꿀 수 있는 Discrete SPRT policy도 SOAP policy입니다. 이에 대한 rank function은 아래와 같습니다.
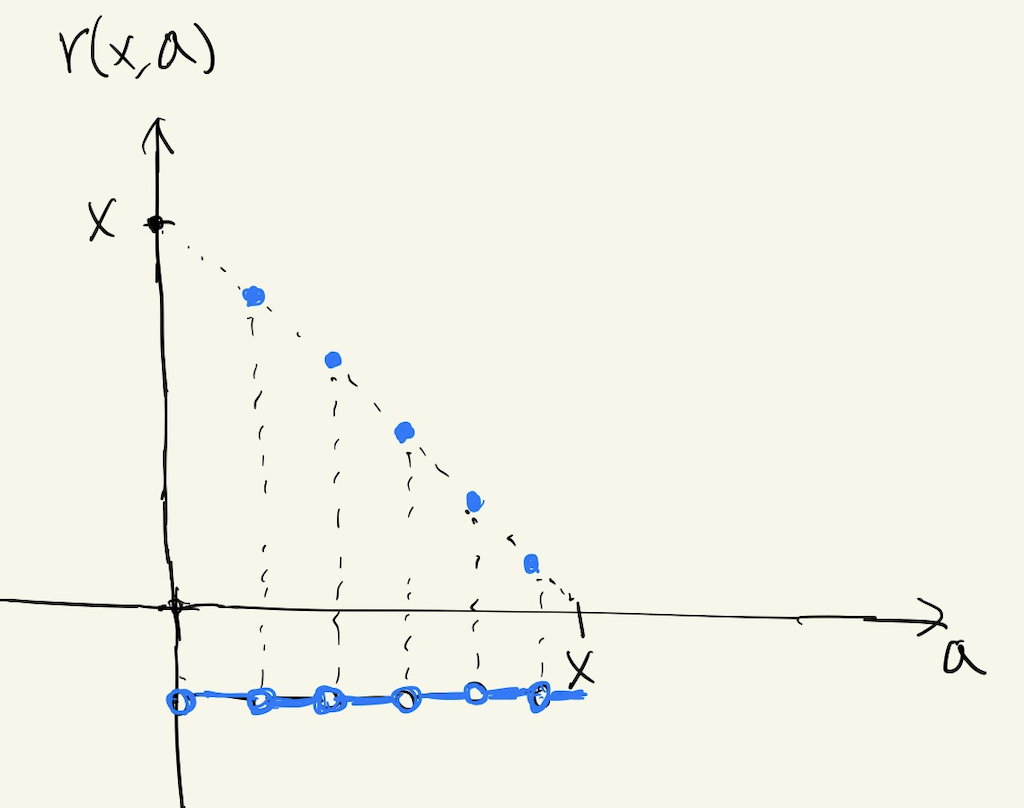
Figure 3. Rank Function for job with size x (Discrete SPRT policy)
What makes $E[T]$ hard to analyze?
SOAP를 통한 분석 이전에도 $E[T]$를 closed form으로 구할 수 있었던 policy로는 SPRT, FCFS 등이 있습니다. 반면, 앞서 살펴본 SEPRT나 Discrete SPRT 등은 $E[T]$에 대한 분석이 까다로웠습니다. 두 그룹에는 다음과 같은 차이가 있습니다.
- SPRT, FCFS 등은 하나의 job에 대해 $a$에 값에 따라 rank function이 monotonely non-increasing한 반면, SEPRT, Discrete SPRT 등은 monotone하지 않습니다.
monotone하지 않은 rank function을 가지는 policy의 $E[T]$를 분석하는 것은 왜 어려울까요? SPRT나 FCFS는 job $i, j$에 대해 server가 $i, j, i, j$ 순으로 처리하는 경우가 없습니다. 즉, $i$를 처리하다가 $j$가 처리되는 경우는 $i$가 종료되었거나 $j$가 새로 추가된 job인 경우밖에 없으며, 후자의 경우는 $j$가 끝나기 전에 $i$를 다시 처리하는 일이 발생하지 않습니다. rank function이 $a$에 대해 non-increasing인 경우 이 성질을 만족함을 쉽게 알 수 있습니다.
non-increasing rank function을 가지는 policy의 경우, arrival부터 처음으로 age가 증가하기 시작할때까지의 waiting time과 그 뒤부터 완료되기까지의 residence time으로 나누어 분석하면 residence time에 delay되는 경우는 rank가 더 낮은 새로운 job이 들어와 끝까지 수행되는 경우만 존재하기 때문에 이를 이용하면 $E[T]$에 대한 analysis가 어렵지 않게 가능함이 알려져 있습니다.
Pessimism Principle
지금부터는 하나의 job에 대해 집중하여 보겠습니다. job의 rank를 worst future rank로 replace한다면 해당 job의 response time에는 어떤 영향을 미칠까요?
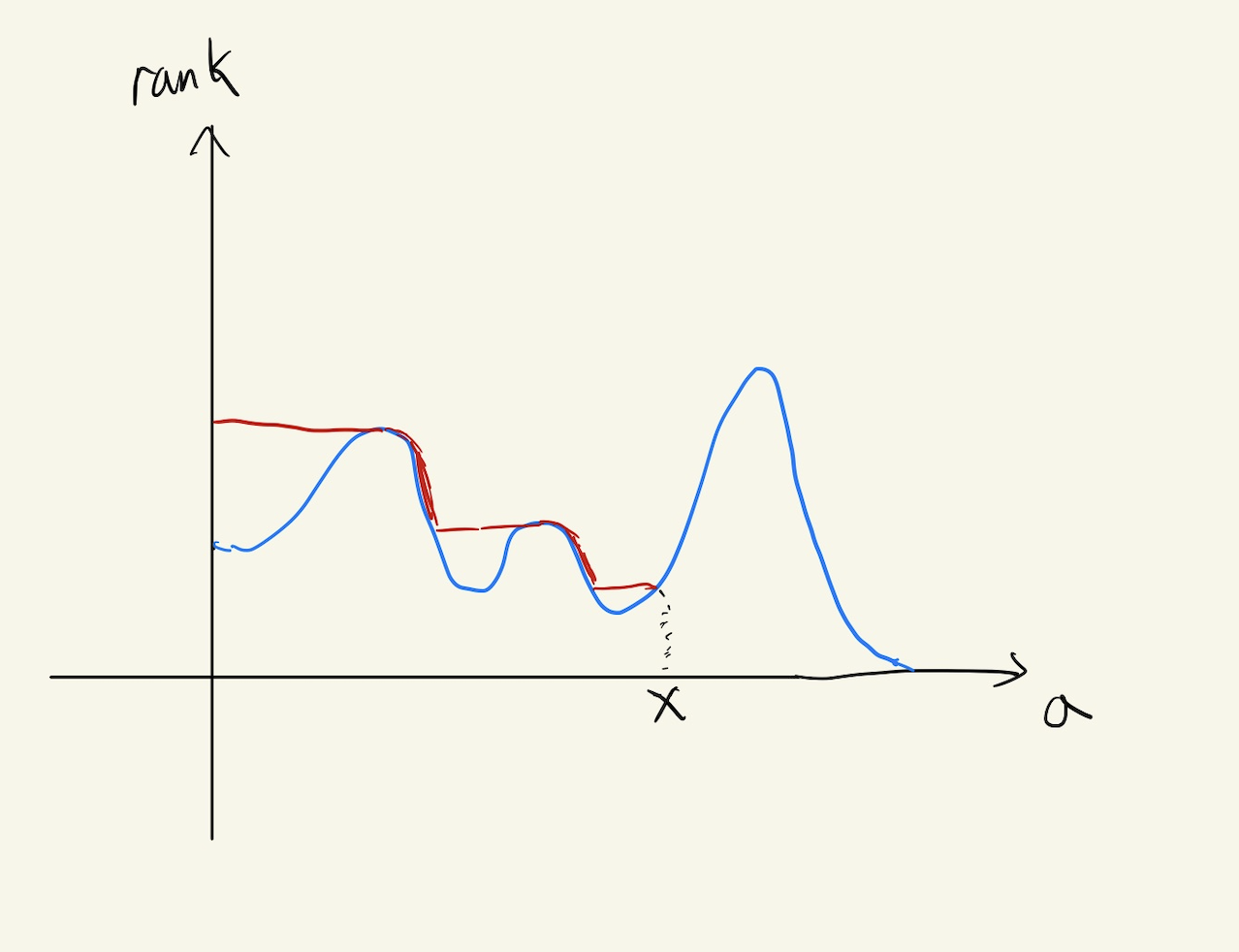
Figure 4. Rank function(blue line) and replaced rank function via pessimism principle(red line)
즉, 위 그림처럼 descriptor가 $d$인 job $J$의 size가 $x$일 때 (이것이 주어지는 information일 필요는 없습니다) $J$의 rank function $r_J(a)$를 $r_{d,x}^{worst}(a) := sup_{t \in [a,x]} r(d,t)$로 replace했다고 가정해봅시다.
Theorem 1. job $J$의 response time은 rank function을 replace하기 전과 후가 동일합니다.
Proof. 다른 job $I$에 대해 delay되는 시간인 delay time $D_{JI}$를 생각해봅시다. $I$가 $J$의 처리가 시작되기 전에 arrive한 경우, $J$가 들어왔을 때 $I$의 rank를 $r_I$라 하면 $r_I$가 $r_J(0)$보다 커지거나 $I$가 종료될 때까지의 시간이 $D_{JI}$가 됩니다. 그리고 이는 $J$의 rank function이 바뀌어도 동일합니다.
$I$가 $J$의 처리가 시작되고 나서 arrive한 경우, arrive한 시점의 $J$의 age $a_J$에 대해 $r_I$가 $r_J(a_J)$보다 커지거나 $I$가 종료될 때까지의 시간이 $D_{JI}$가 됩니다. 이 부분은 $J$의 rank function이 바뀌어도 동일하지만 사실은 rank function이 커짐에 따라 arrive한 시점의 $a_J$가 달라질 수 있습니다.
그러나 rank가 $r_J(a)$와 일치하는 $a$들을 생각해보면 해당 $a$에서 처리되기까지 각 $I$에 대해 delay되는 정도는 동일할 수 밖에 없음을 알 수 있고, 따라서 $D_{JI}$는 rank function을 $sup_{t \in [a,x]} r(d,t)$로 대체하여도 변하지 않습니다. 그러므로 response time 역시 변하지 않습니다. $\blacksquare$
하나의 job에 대해 rank function을 위와 같이 증가시켰을 때 해당 job의 response time은 일정하고 다른 job의 response time은 적어도 증가하지 않음이 보장됩니다.
A Formula for Mean Response Time
앞서 SEPRT, Discrete SPRT, Gittins 등의 policy에 대해 mean response time $E[T]$의 analysis가 이루어지지 못했다는 말씀을 드렸습니다. 하지만 Ziv Scully는 이 논문에서 general하게 모든 SOAP policies에 대해서 적용할 수 있는 $E[T]$에 대한 식을 제시했습니다. 해당 식의 유도는 앞서 말씀드린 Pessimism Principle을 이용하여 각 Job의 delay time을 계산할 수 있도록 만드는 아이디어를 사용합니다. 그러나 식의 계산 도중 확률론적 지식 및 Laplace-Stieltjes transform을 이용하므로 자세한 과정은 생략하고, 식에 사용되는 정의와 결과 자체만을 소개하도록 하겠습니다.
Definitions
$c_d[r] := \inf( a \ge 0 \mid r(d,a) \ge r)$
$X_d^{new}[r] := \min( X_d, c_d[r])$
$(b_{i,d}[r], c_{i,d}[r]) := i\text{-th range of } a \text{ which satisfies } r(a,d) \le r$
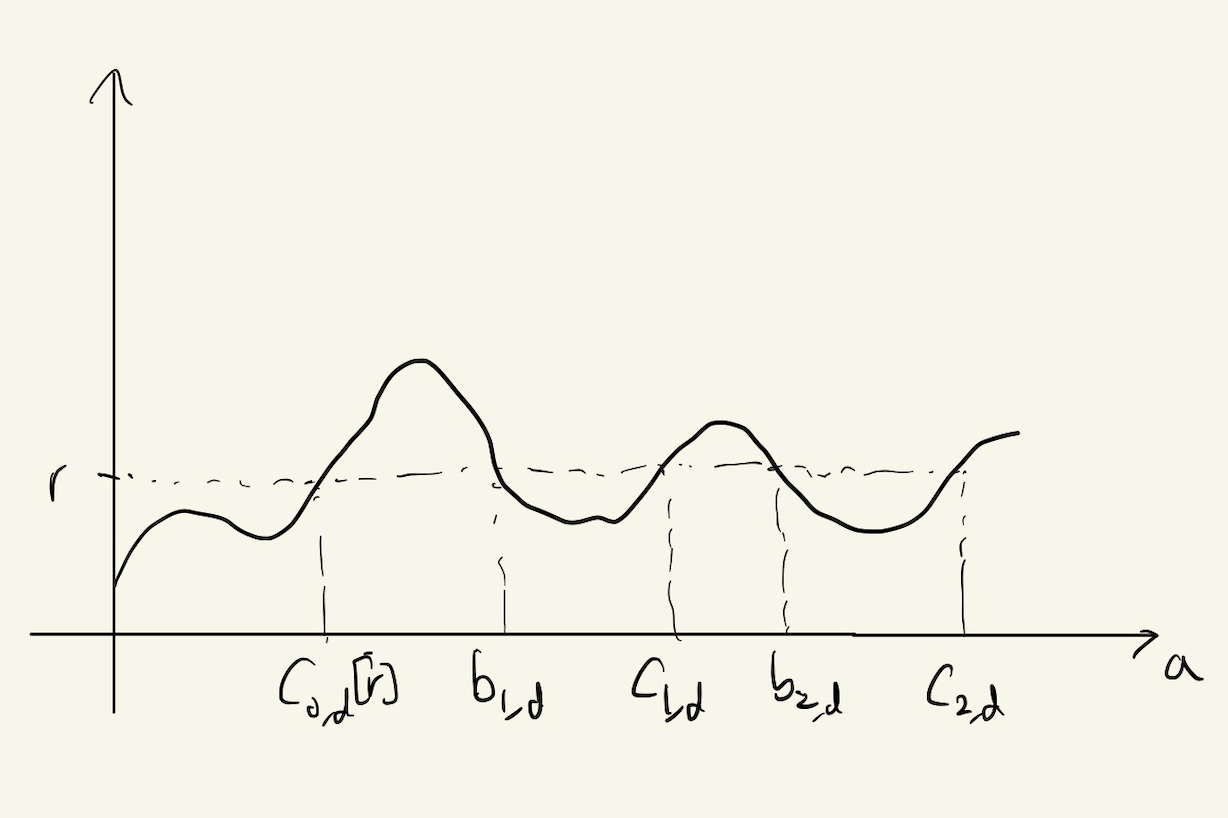
Figure 5. A figure for understanding definitions
$X_{i,d}^{old}[r] =
\begin{cases}
0, & \text{if}\ X_d < b_{i,d}[r]
X_d - b_{i,d}[r] & \text{if}\ b_{i,d}[r] \le X_d < c_{i,d}[r]
c_{i,d}[r] - b_{i,d}[r] & \text{if}\ c_{i,d}[r] \le X_d
\end{cases}$
$\rho^{new}[r] = \lambda E[X^{new}[r]]$
$\rho_{i}^{old}[r] = \lambda E[X_i^{old}[r]]$
이 때, 다음이 성립합니다.
Theorem. descriptor $d$, size $x$인 job의 mean response time은 아래 식과 동일합니다. (단, $r(a) = r_{d,x}^{worst}(a)$ and $r = r_{d,x}^{worst}(0)$)
\[E[T_{d,x}] = \frac{\lambda \sum_{i=0}^{\infty} E[(X_{i,d}^{old}[r])^2] }{2(1-\rho_0^{old}[r])(1-\rho^{new}[r])} + \int_{0}^{x} \frac{da}{1 - \rho^{new}[r(a)]}\]위 식이 어떤 의미인지 알기는 쉽지 않습니다. 예시를 통해 이 analysis로 어떤 model을 해석할 수 있는지 알아봅시다.
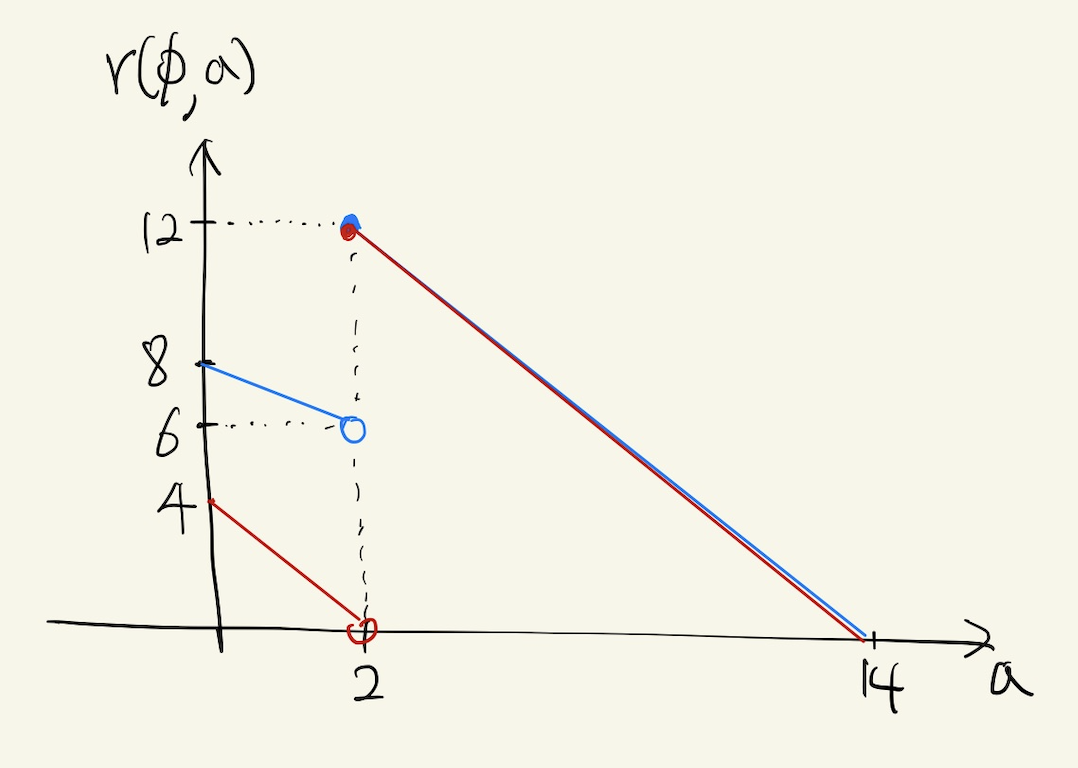
Figure 6. rank function for SEPRT(blue) and Gittins(red)
위 그림은 앞서 살펴본 $X$가 $\frac{1}{2}$ 확률 로 2 또는 14일 떄 SEPRT와 Gittins라는 policy의 rank function 그래프입니다.
SEPRT에서 $c[r] := \inf( a \ge 0 \mid r(a) \ge r)$
이므로 $r \le 8$ 이면 $c[r] = 0$, $8 < r \le 12$ 이면 $c[r] = 2$가 성립합니다.
$X^{new}[r] := \min( X, c[r])$은 $r$은 12 이하이므로 $X^{new}[r] = c[r]$이 됩니다.
또한 다음이 성립합니다.
- $X = 2$인 경우, $r = r_{d,x}^{worst}(0) = 8$
- $X = 14$인 경우, $r = r_{d,x}^{worst}(0) = 12$
그러면 $X_{i}^{old}[r]$의 계산을 위해서는 $r = 8$ 또는 $r = 12$인 경우에 대해서만 계산해주면 됩니다.
$r = 8$인 경우, 위 그래프에서 8 이하인 부분을 생각해보면 $b_0[r] = 0, c_0[r] = 2, b_1[r] = 6, c_1[r] = \infty$임을 알 수 있습니다. 따라서,
- $X_{0}^{old}[8] = 2$
- $X_{1}^{old}[8] = \text{CoinFlip}(0,8)$ ($X=2$일 때 0, $X=14$일 때 8)
- $X_{i}^{old}[8] = 0 (i \ge 2)$
$r=12$일 때는 rank function이 항상 $r$ 이하이므로 $b_0[r] = 0, c_0[r] = \infty$입니다. 따라서, $X_{i}^{old}$는 다음과 같습니다.
- $X_{0}^{old}[12] = \text{CoinFlip}(2,14)$
- $X_{i}^{old}[12] = 0 (i \ge 1)$
위 값들로 $\rho$를 구하면,
- $\rho^{new}[8] = \lambda E[X^{new}[8]] = 0$
-
$\rho_{0}^{old}[8] = \lambda E[X_0^{old}[8]] = 2\lambda$
- $\rho^{new}[12] = \lambda E[X^{new}[12]] = 2\lambda$,
- $\rho_{0}^{old}[12] = \lambda E[X_0^{old}[12]] = \frac{2+14}{2}\lambda = 8\lambda$
계산한 값들을 앞서 소개한 $E[T]$의 계산 식에 대입해봅시다. 먼저 $X=2$인 경우,
\[E[T_{2}^{SERPT}] = \frac{(2^2 + (0^2 + 8^2)/2))\lambda}{2(1-2\lambda)} + \int_{0}^{2} \frac{da}{1 - 0} = \frac{18\lambda}{1-2\lambda} + 2\]이고, $X=14$인 경우
\[E[T_{14}^{SERPT}] = \frac{((2^2 + 14^2)/2)\lambda}{2(1-2\lambda)(1-8\lambda)} + \int_{8}^{14} \frac{da}{1 - 2\lambda} + \int_{0}^{8} da = \frac{50\lambda}{(1-8\lambda)(1-2\lambda)} + \frac{6}{1-2\lambda} + 8\]임을 알 수 있습니다.
현재 예시와 같이 size를 미리 알 수 없지만 $X$의 분포를 알고 있는 상황에서, Gittins는 $E[T]$를 minimize하는 policy로 알려져 있습니다.
Gittins는 Gittins index라고 불리는 식이 큰 job부터 처리하는 policy로, rank function을 Gittins index의 역수로 정의하게 되면 이 역시 SOAP policy임을 알 수 있습니다.
Gittins policy에 대해 좀더 살펴보도록 하겠습니다.
Gittins index는 $G(d,a) := \sup_{\delta > 0}\frac{P[X_d-a \le \delta \mid X_d > a]}{E[\min(X_d-a, \delta) \mid X_d > a]}$로 정의됩니다.
현재 세팅에서 Gittins index를 계산해보면 $G(a)$는 $a < 2$일 때는 $\delta$가 2일 때 $\frac{P[X_d-a \le \delta \mid X_d > a]}{E[\min(X_d-a, \delta) \mid X_d > a]}$가 $\frac{0.5}{E[min(X_d-a,2)]}$로 최대가 되고, $2 \le a < 14$이면 $\delta$가 14일 때 $\frac{1}{E[X_d-a]}$로 최대가 됩니다. 역수를 취해서 rank function을 그려 보면 Figure 6의 그래프와 일치함을 확인할 수 있습니다.
Gittins에서도 SEPRT와 마찬가지로 계산해보면,
$r \le 4$ 이면 $c[r] = 0$, $4 < r \le 12$ 이면 $c[r] = 2$가 성립하고, $X^{new}[r] = c[r]$입니다.
$r$의 값은 아래와 같습니다.
- $X = 2$인 경우, $r = r_{d,x}^{worst}(0) = 4$
- $X = 14$인 경우, $r = r_{d,x}^{worst}(0) = 12$
$r = 4$인 경우, 위 그래프에서 4 이하인 부분을 생각해보면 $b_0[r] = 0, c_0[r] = 2, b_1[r] = 10, c_1[r] = \infty$임을 알 수 있습니다. 따라서,
- $X_{0}^{old}[4] = 2$
- $X_{1}^{old}[4] = \text{CoinFlip}(0,4)$ ($X=2$일 때 0, $X=14$일 때 4)
- $X_{i}^{old}[4] = 0 (i \ge 2)$
$r=12$일 때는 rank function이 항상 $r$ 이하이므로 $b_0[r] = 0, c_0[r] = \infty$입니다. 따라서, $X_{i}^{old}$는 다음과 같습니다.
- $X_{0}^{old}[12] = \text{CoinFlip}(2,14)$
- $X_{i}^{old}[12] = 0 (i \ge 1)$
위 값들로 $\rho$를 구하면,
- $\rho^{new}[4] = \lambda E[X^{new}[4]] = 0$
-
$\rho_{0}^{old}[4] = \lambda E[X_0^{old}[4]] = 2\lambda$
- $\rho^{new}[12] = \lambda E[X^{new}[12]] = 2\lambda$,
- $\rho_{0}^{old}[12] = \lambda E[X_0^{old}[12]] = \frac{2+14}{2}\lambda = 8\lambda$
이를 통해 $E[T]$를 계산하면
\[E[T_{2}^{Gittins}] = \frac{(2^2 + (0^2 + 4^2)/2))\lambda}{2(1-2\lambda)} + \int_{0}^{2} \frac{da}{1 - 0} = \frac{6\lambda}{1-2\lambda} + 2\] \[E[T_{14}^{Gittins}] = \frac{((2^2 + 14^2)/2)\lambda}{2(1-2\lambda)(1-8\lambda)} + \int_{4}^{14} \frac{da}{1 - 2\lambda} + \int_{0}^{4} da = \frac{50\lambda}{(1-8\lambda)(1-2\lambda)} + \frac{10}{1-2\lambda} + 4\]임을 알 수 있습니다.
SEPRT와 Gittins의 $E[T]$를 비교해보면,
$E[T_{2}^{SEPRT}] - E[T_{2}^{Gittins}] = \frac{12\lambda}{1-2\lambda}$
$E[T_{14}^{SEPRT}] - E[T_{14}^{Gittins}] = \frac{-8\lambda}{1-2\lambda}$
로, $X=2$일 확률과 $X=14$일 확률이 반반임을 생각하면 전체 $E[T]$는 Gittins에서 더 작다는 것을 확인할 수 있습니다. 이는 Gittins가 $E[T]$에 대해 Optimal하다는 사실에 반하지 않는 결과입니다.
질문: Pessimism Principle?
Pessimism Principle에 따르면, Gittins 대신 Gittins를 nonincreasing하게 만든 아래와 같은 rank function을 이용해도 $E[T]$가 최소한 더 나빠지지는 않아야 하는 것으로 보입니다. 사실 Pessimism Principle은 기댓값에 대한 것이 아니라 절대적으로 동일하거나 더 나아진다는 Principle이므로, $E[T]$에 국한되지 않더라도 최적의 SOAP policy는 non-increasing rank function를 가져야 할 것 같습니다. 과연 그럴까요?
Figure 6의 Gittins rank function 대신, $a$가 $[0,2]$ 구간에서 $12$로 유지되고 $2 \le a \le 14$이면 Gittins와 동일하게 $14-a$가 되는 rank function을 생각해봅시다. 이 rank function은 Gittins 그래프에서 자신보다 오른쪽의 supremum을 취한 값에 해당하므로, Pessimism principle을 통해 바뀐 rank function으로 보입니다.
그러나, 실제로 $E[T]$를 계산해보면
모든 $0 \le r \le 12$에 대해 $c[r] = X^{new}[r] = 0$이고, $X$의 값 $x$에 관계없이 $r = r_{d,x}^{worst}(0) = 12$,
- $X_{0}^{old}[12] = \text{CoinFlip}(2,14)$
- $X_{i}^{old}[12] = 0 (i \ge 1)$
따라서,
\[E[T_{2}] = \frac{((2^2 + 14^2)/2)\lambda}{2(1-8\lambda)} + \int_{0}^{2} \frac{da}{1 - 0} = \frac{50\lambda}{1-8\lambda} + 2\] \[E[T_{14}] = \frac{((2^2 + 14^2)/2)\lambda}{2(1-8\lambda)} + \int_{0}^{14} \frac{da}{1 - 0} = \frac{50\lambda}{1-8\lambda} + 14\]로, $E[T]$를 계산해보면 Gittins에 비해 큰 값임을 알 수 있습니다. 무엇이 잘못되었을까요?
바로 Pessimism principle을 적용할 때 오류가 있었습니다.
$r_{d,x}^{worst}(a) := sup_{t \in [a,x]} r(d,t)$을 대신 대입할 때 $[a, \infty]$ 구간이 아니라 $[a, x]$ 구간의 supremum을 취해야 하기 때문에,
$X = 2$인 경우에는 $[0,2]$ 구간에서 rank function이 12가 아닌 4가 되었어야 하는 것입니다.
물론 이 경우에도 job의 rank function은 $a$에 대해 non-increasing이므로 non-increasing한 rank function만 보면 된다는 생각은 틀리지 않을 수 있어 보입니다.
그러나, 현재 예시에서와 같이 size $x$의 정보는 descriptor $d$에서 알 수 없을 수 있고, 그 경우 Pessimism Principle을 적용했을 때처럼 size에 따라 rank function이 달라지도록 policy를 설정할 수가 없게 됩니다.
즉, Pessimism Principle을 적용한 Policy는 $r(d,a)$ rank function으로 정의 자체가 불가능해질 수 있습니다. 이에 SOAP Policy 중 최적의 policy를 찾을 때는 non-increasing한 rank function이외에도 Gittins, SEPRT처럼 monotone하지 않은 rank function을 가지는 Policy도 고려해야 합니다.
Conclusion
이상으로, sceduling policy들과 analysis하고자 하는 일반적인 세팅인 M/G/1 Queue와 같은 개념을 먼저 알아보고, rank로 정의되는 SOAP policy가 무엇인지 그리고 rank function을 어떻게 주느냐에 따라 어떤 policy가 나올수 있는지에 대해 알아보았습니다. 나아가 analysis에 이용되는 Pessimism Principle, 그리고 SOAP policy의 mean response time을 구하는 일반적인 식에 대해서까지 알아보고, 실제로 예시를 통해 SEPRT와 Gittins에서의 mean response time을 비교해보기도 했습니다.
앞서 살펴보았듯이 현재 우리가 사용하는 컴퓨터와 같은 경우 여러개의 코어를 가지고 있으므로 M/G/1 Queue 모델이 아니라 M/G/k 모델에 가깝다고 할 수 있습니다. 여러 server가 존재하는 M/G/k 모델에 대해 analysis할 수 있는 도구로는 WINE이라는 개념이 있습니다. 이 역시 SOAP를 도입한 Ziv Scully의 thesis 에서 찾아볼 수 있으므로 혹시 scheduling, queueing theory에 관심이 있거나 이 글보다 더 자세한 내용에 대해 알고싶으신 분들은 해당 글에서 좀더 심화된 내용을 이해해 볼 수 있을 것입니다.