ainta's profile image

ainta

March 19, 2023 00:00

Preliminaries

Multilinear Extension

$f(x_1, \cdots ,x_v) = \lbrace 0,1 \rbrace^v \rightarrow \mathbb{F}$ 에 대해,

$f$의 domain $\lbrace 0,1 \rbrace^v$ 내에서 $f(x_1, \cdots ,x_v) = g(x_1, \cdots ,x_v)$가 성립하는 multivariable polynomial $\overline{f}$가 각각의 variable $x_1, \cdots, x_v$에 대해 linear일 때 $\overline{f}$를 $f$의 multilinear extension이라 합니다.

How to build Multilinear Extension

\[\overline{f}(x_1, \cdots, x_v) = \sum_{(a_1, \cdots, a_v) \in \{0,1\}^v} f(a_1, \cdots, a_v) \prod_{i=1}^v (a_ix_i + (1-a_i)(1-x_i))\]

위 식에서 $x_1, \cdots, x_v \in {0,1}^v$ 인 경우 모든 $i$에 대해 $x_i = a_i$가 성립할 때만 오른쪽 값이 1이 되고 그 외에는 0이므로 $\overline{f}(x_1, \cdots, x_n) = f(x_1, \cdots, x_n)$임을 쉽게 확인할 수 있습니다.

Multilinear Extension의 유일성

$f$의 Multilinear extension $g, h$에 대해, $g-h$는 $\lbrace0,1 \rbrace^v$에서 함수값이 0인 multivariable polynomial이며 각각의 $x_1, \cdots, x_v$에 대해서는 linear입니다. $g-h$가 $0$이 아니라고 가정해봅시다. $g-h$에서 total degree가 가장 작은 항 중 하나를 뽑아 $c ( x_{i_1}x_{i_2}\cdots x_{i_k})$라 할 때 (상수 $c \neq 0$), $x_{i_j}$들은 1, 그 외의 variable은 0으로 설정하면 이에 대한 함수값은 $c \neq 0$일 수 밖에 없으므로 이는 $g-h$가 $\lbrace0,1 \rbrace^v$에서 함수값이 $0$이어야 한다는 사실에 모순입니다. 따라서, 함수 $f$의 multilinear extension은 유일합니다.

Sum-check Protocol

rkm0959님의 소프트웨어 멤버십 블로그 글에서 자세히 설명되어 있습니다. 간단하게 다시 설명하자면,

유한체 $\mathbb{F}$ 위에 정의된 polynomial $f$에 대해, Prover는

\[H = \sum_{x_1, \cdots, x_v \in \lbrace 0,1 \rbrace} f(x_1, \cdots ,x_v)\]

가 성립함을 보이고자 합니다. 가장 간단하게는 verifier가 직접 $2^v$번 $f$를 evaluate하면 되지만, verifier의 cost는 되도록 줄이는 것이 목표입니다.

처음에 Prover는 $H$ 값을 Verifier에게 보냅니다. 그 이후로 $v$번의 라운드에 걸쳐 프로토콜이 진행됩니다.

첫 번째 라운드에서 Prover는 univariable polynomial $f_1(X) = \sum_{x_2, \cdots, x_v \in \lbrace 0,1 \rbrace} f(X, x_2, \cdots ,x_v)$ 을 verifier에게 전달합니다. verifier는 $f_1(0) + f_1(1) = H$가 성립하는지 확인합니다. 그리고 $\mathbb{F}$에서 랜덤한 $r_1$을 골라 Prover에게 전달합니다.

$i$번째 라운드에서 Prover는 univariable polynomial

$f_i(X) = \sum_{x_{i+1}, \cdots, x_v \in \lbrace 0,1 \rbrace} f(r_1, \cdots, r_{i-1}, X, x_{i+1}, \cdots ,x_v)$ 을 verifier에게 전달하고,

verifier는 $f_i(0) + f_i(1) = f_{i-1}(r_i)$가 성립하는지 확인한 후 $\mathbb{F}$에서 랜덤한 $r_{i}$를 골라 Prover에게 전달합니다. $v$번의 라운드가 종료된 후에 verifier는 마지막으로 $f_v(r_v) = f(r_1,r_2, \cdots, r_v)$가 성립하는지 $f$를 직접 evaluate하여 확인한 후 Accept 여부를 결정합니다. 이 때 verifier의 계산량은 $f$를 한 번 evaluate할 때 걸리는 시간을 $T$라 할 때 $v + T$로, 일일이 더했을 때 걸리는 시간인 $2^vT$에 비해 현저히 적음을 알 수 있습니다.

Prover가 올바르지 않은 $H$로 Verifier를 통과할 확률, 즉 Soundness error는 Schwartz-Zippel Lemma에 따르면 최대 $dv/\mathbb{F}$가 됩니다. ($d$: $f$의 total degree)

Arithmetic Circuit

Arithmetic Circuit 이란 두 input $y,z$에 대해 $y+z$를 output으로 가지는 $\text{Add}(y,z)$ 게이트와 $y \times z$를 output으로 가지는 $\text{Mul}(y,z)$ 게이트로 이루어진 Circuit을 뜻합니다. 다음은 간단한 Arithmetic Circuit을 나타낸 그림입니다.

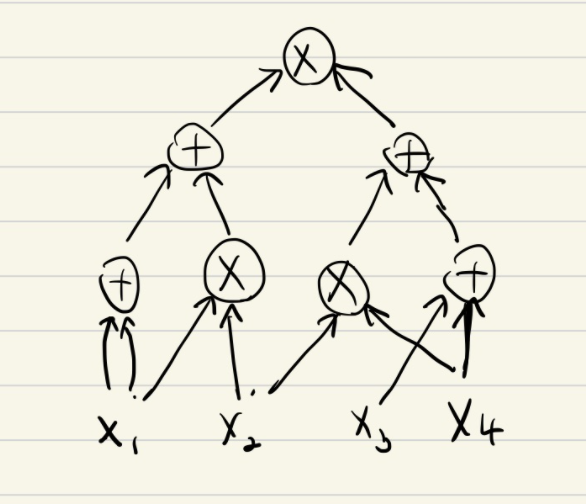
Figure 1. Arithmetic circuit for $(2x_1 + x_1x_2)(x_2x_4 + x_3 + x_4)$

GKR protocol

GKR protocol은 public한 Arithmetic Circuit $C$가 주어져 있을 때, $C(X) = Y$를 만족하는 input $X$를 알고 있음을 증명할 수 있는 방법입니다(ARgument of Knowledge). 이는 Groth16 Protocol, PLONK 등이 달성하고자 하는 목적과 동일합니다. 단, naive GKR protocol은 Groth16처럼 zero-knowledge proof를 주지는 않습니다.

GKR protocol의 세팅에서, Prover는 $C(X) = Y$를 만족하는 input $X$를 본인이 알고 있음을 증명하려고 합니다. Verifier는 Prover가 $C(X) = Y$를 만족하는 $X$를 진짜 알고 있는지 검증하려 합니다.

가장 간단한 증명은 $X$ 자체를 보내는 것입니다. 그러나, $X$가 큰 경우 proof size가 커진다는 문제점이 발생합니ㅏ다.

Arithmetic Circuit의 depth는 가장 많은 gate를 통과하는 input이 통과하는 gate 수로 정의됩니다. depth $d$인 circuit의 output layer를 layer $0$, input layer를 layer $d$라 합니다.

편의성을 위해 layer $i$에는 $2^{k_i}$개의 gate가 존재하고, 각각의 gate에는 $0, 1, \cdots, 2^{k_i}-1$의 label이 붙어 있다고 하겠습니다.

$C(X) = Y$를 만족하는 input $X$를 알고 있는 Honest Prover를 생각합시다. 이 Prover는 input $X$를 대입했을 때 각 gate에 무슨 값이 들어있는지 알 수 있을 것입니다.

$W_i(x):=$ layer $i$의 label $x$인 게이트의 값 ($x \in \lbrace 0,1 \rbrace^{k_i}$로 생각할 수 있음) 이라 하면

다음과 같은 식이 성립합니다.

\[W_i(z) = \sum_{x,y \in \lbrace 0,1 \rbrace^{k_{i+1}}} [add_i(z,x,y)(W_{i+1}(x)+W_{i+1}(y)) + mul_i(z,x,y)(W_{i+1}(x)W_{i+1}(y))]\]

여기서, $add_i(z,x,y)$ 는 layer $i$의 label $z$ 게이트가 Add 게이트이며 layer $i+1$의 label $x, y$인 두 게이트를 input으로 가질 때만 1이고, 그 외에는 0인 함수입니다. $mul_i(z,x,y)$도 Mul 게이트에 대해 같은 방식으로 정의합니다.

위 식을 Multilinear extension에 적용하면

\[\overline{W_i}(z) = \sum_{x,y \in \lbrace 0,1 \rbrace^{k_{i+1}}} [\overline{add_i}(z,x,y)(\overline{W_{i+1}}(x)+\overline{W_{i+1}}(y)) + \overline{mul_i}(z,x,y)(\overline{W_{i+1}}(x)\overline{W_{i+1}}(y))]\]

이 됩니다. 여기서 각각의 함수들은 polynomial이므로, 위의 sum-check protocol을 적용할 수 있습니다!

위 식에서 더해지는 대괄호 내의 값을 $tp(x,y)$라 하면, 처음에는 마지막 output인 $\overline{W_0}(0)$에 대한 sum-check protocol을 실행할 것이고, 해당 sum-check protocol에서 마지막에는 $tp(x_r,y_r)$의 값을 verifier가 계산해야 합니다.

그 중 $\overline{add_i}$와 $\overline{mul_i}$의 값은 크지 않은 시간에 계산할 수 있다고 가정하는 데에 무리가 없습니다. 그러나 $\overline{W_{i+1}}(x), \overline{W_{i+1}}(y)$의 계산을 위해서는 arithmetic circuit을 계산해야 한다는 문제가 있습니다.

아이디어는 이를 Prover가 $\overline{W_{i+1}}(x), \overline{W_{i+1}}(y)$를 알고 있다를 증명하는 문제로 다시 치환하는 것입니다. 그러면 layer를 하나씩 내려가다가 마지막 input이 되는 layer $d$에서는 circuit을 계산할 필요가 없기 때문에 이 부분이 해결됩니다.

하지만 처음에 $\overline{W_0}(0)$에 대한 claim이 $\overline{W_1}(x_1), \overline{W_1}(y_1)$에 대한 claim으로 치환되는 현재와 같은 구조에서는 layer가 하나씩 늘어날 때마다 보여야 하는 문제가 2배씩 늘어나는 문제가 발생합니다.

다행히도, 아래와 같은 식을 대신 이용하면 layer $i$의 두 claim을 layer $i+1$의 두 claim으로 치환할 수 있습니다.

\[a\overline{W_i}(u) + b\overline{W_i}(v) = \sum_{x,y \in \lbrace 0,1 \rbrace^{k_{i+1}}} [(a \times \overline{add_i}(u,x,y) + b \times \overline{add_i}(v,x,y))(\overline{W_{i+1}}(x)+\overline{W_{i+1}}(y)) + (a \times \overline{mul_i}(u,x,y) + b \times \overline{mul_i}(v,x,y))(\overline{W_{i+1}}(x)\overline{W_{i+1}}(y))]\]

그러면 layer가 내려갈 떄 마다 claim의 개수가 증가하는 것을 막을 수 있습니다.

Linear Proving Time

Linear-time sumcheck for a multilinear function

sum-check protocol의 $i$번째 라운드에서, prover는 $x_i$에 대한 univariate polynomial

\[f_i(x_i) = \sum_{b_{i+1}, \cdots , b_{l} \in \lbrace 0,1 \rbrace} f(r_1, \cdots, r_{i-1}, x_i, b_{i+1}, \cdots, b_l)\]

을 verifier에게 전달합니다.

$f$가 multilinear function일 때, $f_i(x_i) = f_i(0) + x_i(f_i(1)-f_i(0))$이 성립하므로, $f_i(0)$ 및 $f_i(1)$을 알고 있다면 $f_i(x_i)$을 결정할 수 있습니다. $r_1, \cdots, r_{i-1}$은 $\lbrace 0,1 \rbrace$에 포함되는 값들이 아닌데, prover가 verifier에게 전달해야하는 값을 total linear time(optimal time)에 어떻게 하면 계산할 수 있을까요? (여기서 linear-time = $O(2^l)$)

problem solving에서의 하나의 문제로 생각하면 이를 보다 간단하게 해결할 수 있습니다.

$A[0], \cdots A[2^l-1]$가 주어져 있을 때, $D[i][t]$를 $f(r_1, \cdots, r_{i-1}, r_i, t_1, \cdots, t_{l-i})$ (단, $0 \le i \le l$, $t \in \lbrace 0,1 \rbrace^{l-i}$) 의 형태로 정의해봅시다.

verifier로부터 $r_{i-1}$가 올 때마다 $D[i-1]$의 값들을 모두 빠르게 계산해낼 수 있다면

$\sum_{b_{i+1}, \cdots , b_{l} \in \lbrace 0,1 \rbrace} f(r_1, \cdots, r_{i-1}, 0, b_{i+1}, \cdots, b_l)$과 $\sum_{b_{i+1}, \cdots , b_{l} \in \lbrace 0,1 \rbrace} f(r_1, \cdots, r_{i-1}, 1, b_{i+1}, \cdots, b_l)$ 을 구할 수 있으므로 $f_i(x_i)$를 verifier에게 전달할 수 있게 됩니다.

그리고 이는 $D[i][t]$ = $r_i \cdot D[i-1][1 \mid\mid t] + (1 - r_i) \cdot D[i-1][0 \mid\mid t]$ (단, $a \mid\mid b$는 $a$ 뒤에 $b$가 붙은 bitstring)이라는 간단한 점화식으로 구할 수 있습니다.

Linear-time sumcheck for multilinear functions

multilinear function $f, g$에 대해, $\sum_{x \in \lbrace 0,1 \rbrace^{k}} f(x)g(x)$ 에 대해서도 sum-check protocol을 적용할 수 있습니다.

$fg$는 multilinear function은 아니지만, 각 variable에 대해 모든 항이 2차 이하인 함수입니다.

먼저, $f$, $g$에 대해 동일한 방법으로 $D_f[i-1], D_g[i-1]$를 계산할 수 있습니다. 이를 이용해 $t = 0, 1, 2$에 대해 $\sum_{b_{i+1}, \cdots , b_{l} \in \lbrace 0,1 \rbrace} (f \cdot g)(r_1, \cdots, r_{i-1}, t, b_{i+1}, \cdots, b_l)$를 계산하면 lagrange interpolation을 이용해 constant time에 $f_i(x_i)$를 구성할 수 있습니다.

Linear-time sumcheck for functions used in GKR

GKR protocol에서 사용하는 식은 아래와 같습니다.

\[a\overline{W_i}(u) + b\overline{W_i}(v) = \sum_{x,y \in \lbrace 0,1 \rbrace^{k_{i+1}}} [(a \times \overline{add_i}(u,x,y) + b \times \overline{add_i}(v,x,y))(\overline{W_{i+1}}(x)+\overline{W_{i+1}}(y)) + (a \times \overline{mul_i}(u,x,y) + b \times \overline{mul_i}(v,x,y))(\overline{W_{i+1}}(x)\overline{W_{i+1}}(y))]\]

이제 위 식에서 sum-check protocol을 적용하려고 합니다. 만약,

\[\sum_{x,y \in \lbrace 0,1 \rbrace^{k}} U(z,x,y)\overline{W}(x)\overline{W}(y)\]

와 같은 형태의 식에서 sum-check protocol을 적용할 수 있다면 GKR protocol에서도 쓸 수 있음을 쉽게 생각할 수 있습니다.

이 때 $add, mul$에 대항하는 $U(z,x,y)$의 경우 $x,y \in \lbrace 0,1 \rbrace^{k}$ 중 최대 하나의 $(x,y)$ 쌍에서만 0이 아닌 값을 가진다는 조건을 줄 수 있습니다. 함수

\[\overline{H_z}(x) = \sum_{y \in \lbrace 0,1 \rbrace^{k}} U(z,x,y) \overline{W}(y)\]

에 대해, 모든 $x \in \lbrace 0,1 \rbrace^{k}$에 대한 $H_z$값을 어렵지 않게 계산할 수 있습니다. 그러면 처음의 식을

\[\sum_{x \in \lbrace 0,1 \rbrace^{k}} \overline{H_z}(x)\overline{W}(x)\]

와 같이 쓸 수 있고, $\overline{H_z}(x)\overline{W}(x)$ 각각은 $x$에 대한 multilinear polyinomial이므로 이에 대해 sum-check protocol을 적용할 수 있습니다.

More about GKR Protocol

이때까지 살펴본 GKR protocol은 Interactive proof이지만, Fiat-Shamir transform을 통해 non-interactive한 버전으로 쉽게 변환 가능합니다. GKR protocol이 처음 제시되었을 때는 proving time이 linear가 아니었고, 위에 소개한 방법은 Libra 에서 사용한 개선된 방법입니다. Libra에서는 이외에도 zero-knowledge sumcheck을 이용하여 zero-knowledge proof를 제공할 수 있도록 개선하였습니다.

Modern zk-SNARK

Modern zk-SNARK는 보통 Polynoimal interactive oracle proof(PIOP)와 Polynomial commitment scheme라는 두가지 구성 요소로 이루어지며, 오늘 살펴본 내용은 PIOP에 관련된 내용입니다. PIOP에는 최근 가장 흔하게 사용되는 PLONK 이외에 앞서 말씀드린 Libra, Marlin, Sonic, 그리고 오늘 소개드린 multilinear extenstion과 sum-check protocol을 이용하는 HyperPLONK 등이 있습니다. HyperPLONK는 PLONK와 달리 fft가 필요하지 않다는 장점이 있습니다. Polynomial Commitment Scheme은 KZG, Fri, DARK 등이 존재합니다. 다음에 기회가 된다면 이에 관련하여 보다 깊은 포스트를 작성하도록 하겠습니다.

References

• Justin Thaler. “Proofs, Arguments, and Zero-Knowledge”

• Tiancheng Xie, Jiaheng Zhang, Yupeng Zhang. “Libra: Succinct Zero-Knowledge Proofs with Optimal Prover Computation”