ainta's profile image

ainta

April 24, 2023 00:00

Error-correcting code

$[n, k, d]$ code: 길이 $k$인 message $m$을 길이 $n$인 codeword $Enc(m)$으로 인코딩하는 $Enc$에 대해, 서로 다른 두 message의 codeword의 hamming distance (서로 다른 entry의 개수)가 항상 $d$ 이상일 때 이를 $[n, k,d]$ code라 합니다. 이 때 가장 가까운 두 codeword가 서로 다른 비율을 나타내는 $\Delta = \frac{d}{n}$을 code의 relative distance라고 부릅니다.

Example: Repitition code

예를 들어, “0101”을 “000111000111”로 encoding하는, 원래의 비트를 세 번씩 반복하는 repitition code의 경우 이는 $[3k, k, 3]$ 코드이고, 최대 하나의 오류가 발생할 경우 이를 올바르게 correct할 수 있습니다.

Linear error-correcting code

codeword의 linear combination 또한 codeword가 될 때 이를 Linear code라 합니다. $[n, k, d]$ linear code는 $[n, k, d]$ code의 성질을 만족하는 linear code를 뜻합니다. Linear code의 encoding 과정은 $\mathbb{F}_p^k$ 에서 $\mathbb{F}_p^n$으로 가는 linear operator이므로 $n \times k$ 행렬로 나타낼 수 있습니다.

Example: Reed-Solomon code

Encoding: $\mathbb{F}_p^k \rightarrow \mathbb{F}_p^n$

길이 $k$의 message를 degree $k-1$인 polynomial로 생각할 수 있습니다. $\mathbb{F}_p$의 $n$-th root of unity $\omega$에 대해, $\omega^1, …, \omega^n$에서의 evaluation을 codeword로 하는 encoding을 Reed-Solomon code라 합니다.

degree $k-1$ 이하의 0이 아닌 polynomial은 최대 $k-1$개의 solution을 가지므로, 이는 $d = n-(k-1) = n-k+1$인 code입니다. 또한, $j = 0, \cdots, k-1$에 대해 $\omega^{1j}, …, \omega^{nj}$ 를 column으로 가지는 matrix가 이 code의 operator라고 볼 수 있고, 따라서 이는 $[n, k, n-k+1]$ Linear code가 됩니다. $n=2k$인 경우, $\frac{1}{2}$ 이상의 relative distance를 가짐을 확인할 수 있습니다.

Reed-Solomon code의 encoding은 $\omega^1, …, \omega^n$에서의 evaluation이 필요하고, FFT($\mathbb{F}_p$에서 이므로 NTT로 구현)를 이용하면 $O(n \log n)$시간에 작동하는 알고리즘이 있습니다.

Generalized Spielman code

Reed-Solomon code는 $O(n \log n)$ 시간이 소요됩니다. Repitition code는 relative distance가 $O(1/n)$ 수준입니다. 앞으로 알아볼 code는 Generalized Spielman code라고 불리며, constant scale의 relative distance를 가지면서 linear time에 인코딩을 할 수 있는 linear code입니다.

Generalized Spielman code가 흥미로운 점은 전혀 관련이 없어보이는 개념인 graph의 lossless expander를 사용한다는 점입니다.

Lossless Expander

왼쪽 정점들의 집합 $L$의 모든 정점 $v$의 차수가 $g$로 동일한 bipartite graph $G = (L,R,E)$가 있습니다. $\lvert L \rvert = k, \lvert R \rvert = k’ = \alpha k$라 합시다. 이 때, 상수 $0 < \epsilon < 1, 0 < \delta$에 대해 다음 조건을 만족하는 경우 $G$를 $(k, k’;g)$-lossless expander 라 합니다.

• Expansion: $\lvert S \rvert \le \delta k /g$를 만족하는 모든 $S \subset L$ 에 대해, $N(S) \ge (1-\epsilon) g \lvert S \rvert$가 성립한다.

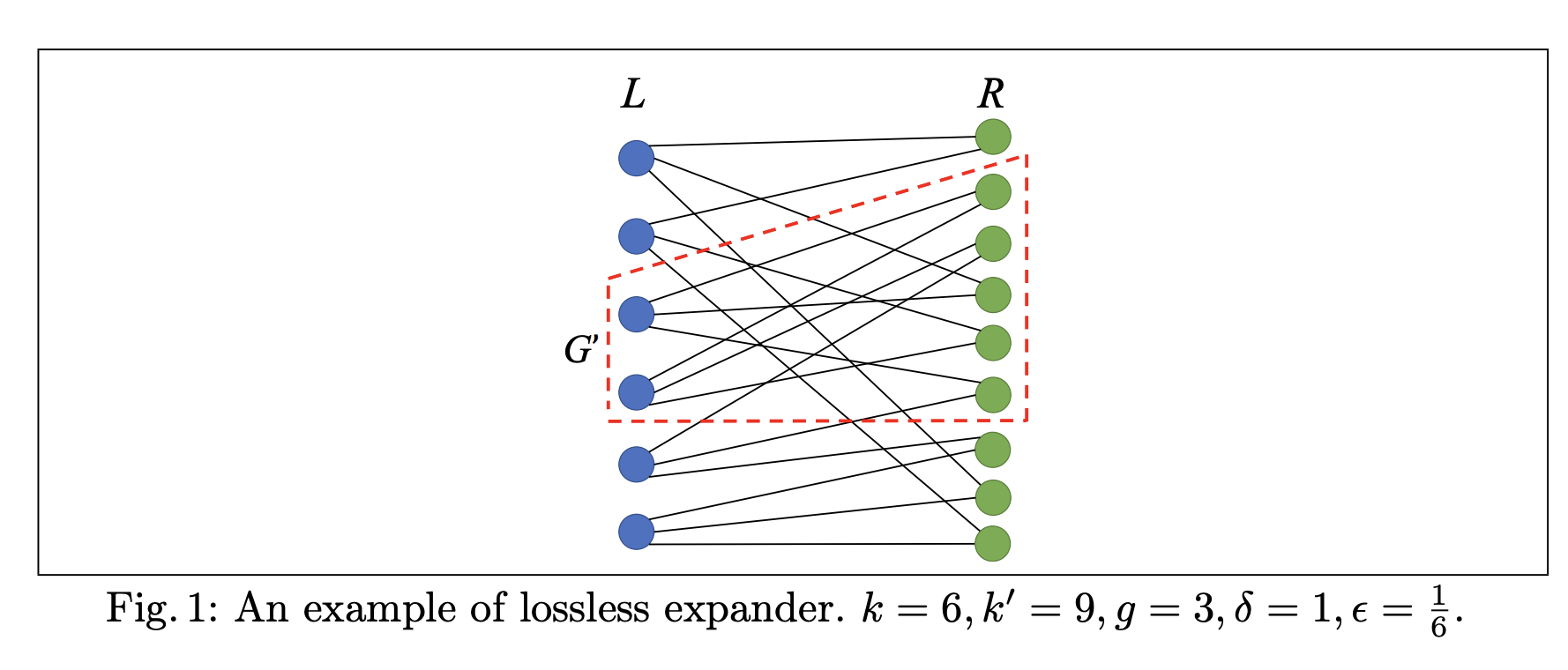
위 Fig 1은 $\delta k/g = 6/3 = 2$ 이므로 $L$의 크기 2인 부분집합들의 neighbor의 size가 $(1-\epsilon)g \cdot 2 = 5$ 이상인 경우 expansion 성질을 만족하는 것인데, 실제로 $L$에 두 개 이상의 neighbor가 겹치는 정점쌍이 없으므로 조건을 만족함을 알 수 있습니다.

Lossless expander의 정의에 대한 Intuition을 간단해 소개하겠습니다. $L$의 각 정점의 차수는 $g$이고, $L$에서 임의의 부분집합 $S$를 잡은 경우 $S$가 작으면 $\lvert N(S) \rvert$가 $g \lvert S \rvert$보다 조금 작을 확률이 높을 것이고 $S$가 커짐에 따라 겹치는 오른쪽 neighbor가 많아져 $g \lvert S \rvert$와의 차이가 커지는 경향을 띤다고 생각할 수 있을 것입니다.

특히 $\lvert S \rvert > \frac{k’}{g(1-\epsilon)} = \frac{\alpha k}{g(1-\epsilon)}$인 경우 $N(S) \ge (1-\epsilon) g \lvert S \rvert > k’$를 만족하는것이 불가능하고, 이에 neighbor들이 잘 겹치지 않는 $S$의 크기의 bound에 해당하는 rate $\delta$가 lossless expander의 정의에 포함되게 되었습니다.

즉, 이분그래프 $G$가 lossless expander라는 것은 $G$의 왼쪽 정점에서 특정 크기 이하의 부분집합을 골랐을 때, 그 집합의 정점들의 neighbor가 $\epsilon$ 이하의 비율로만 겹치게 됨을 뜻합니다.

Construction of Generalized Spielman code

그러면 갑자기 등장한 Lossless expander라는 개념이 어떻게 Linear code에 사용되는지에 대해 알아보겠습니다. 먼저 세팅은 아래와 같습니다:

• $G(t) = (L(t),R(t),E(t))$는 $\lvert L(t) \rvert = 2^t, \lvert R(t) \rvert = 2^{t-1}$를 만족하는 lossless expander
• $A(t)$는 $G(t)$에서 $i \in [2^t], j \in [2^{t-1}]$에 대해 $(i,j) \in E(t)$이면 $A(t){ji} = 1$, $(i,j) \notin E(t)$이면 $A(t){ji} = 0$인 $2^{t-1}$ by $2^t$ matrix

앞으로 size $2^t$인 message를 size $2^{t+2}$인 codeword로 인코딩하는 $E_C^t$를 만들 것입니다. $E_C^t$는 아래와 같은 방법으로 재귀적으로 generate할 수 있습니다:

Algorithm 1. Encoding of Generalized Spielman code

Setting

• Given message $m$ of size $2^t$

Algorithm

1. $m_1 = A(t)m$ 는 size $2^{t-1}$. 따라서, $c_1 = E_C^{t-1}(m_1)$은 크기 $2^{t+1}$의 codeword.
2. $c_2 = A(t+1)c_1$은 size $2^t$의 codeword.
3. $m, c_1, c_2$를 concatenate한 것을 $c$라 할 때, $E_C^t(m)=c$로 인코딩.

이 알고리즘에 대해, 다음이 성립함이 알려져 있습니다.

Theorem 1(Generalized Spielman code, [DI14]). $t \in \mathbb{N}$에 대해 각각의 $G(t)$가 $\lvert S \rvert \le \delta \lvert L \rvert/g$에 대해 $\lvert N(S) \rvert \ge (1-\epsilon)g\lvert S \rvert$를 만족하는 lossless expander인 $G(t)$들과 그로 만든 행렬 $A(t)$들이 주어졌다고 하자 (단, $\epsilon < 1/4, g \ge 2$) . 이 때, Algorithm 1의 $E_C^t$로 생성한 code는 constant relative distance $\frac{\delta}{4g}$를 가지는 Linear code이다.

위 정리를 증명하기 위해 다음과 같은 Lemma를 먼저 소개하겠습니다.

Lemma 1. Linear code에서 가장 가까운 codeword의 distance는 0이 아닌 codeword 중 가장 nonzero entry가 적은 codeword의 nonzero entry의 개수와 동일하다.

이제부터는 벡터 $x$의 nonzero entry의 개수를 $x$의 weight이라고 부를 것입니다.

먼저, $[n, k]$ Linear code의 encoding은 행렬을 곱해진 것이므로, $0^k$는 $0^n$으로 갑니다. 그리고, $Enc(x_1)$의 $Enc(x_2)$의 $i$번째 entry가 다른 것은 $Enc(x_1 - x_2)$의 $i$번째 entry가 nonzero인것과 동치입니다. 따라서, Linear code에서 0이 아닌 codeword의 minimum weight을 $d$라 하면 이는 $[n, k, d]$ Linear code가 됩니다. $\blacksquare$

이제 정리를 증명해 봅시다. 다음과 같은 Claim을 보이면 충분합니다.

Claim. $E_C^{t-1}$가 constant relative distance $\Delta$를 가질 때, $E_C^{t}$ 역시 constant relative distance $\Delta’ = \min(\Delta, \frac{\delta}{4g})$를 가진다.

$m$이 $0$이 아닐 때, $E_C^t(m) = Concatenate(m, c_1, c_2)$의 weight이 $4k\Delta’$이상임을 보이면 Claim이 증명됩니다. 즉, $m, c_1, c_2$의 weight 합이 $4k\Delta’$ 이상임을 보이면 됩니다.

먼저, $m$의 weight이 $4k\Delta’$개 이상인 경우는 이를 만족합니다. $m$의 weight이 $4k\Delta’$ 이하인 경우, $m$의 nonzero entry에 해당하는 $G(t)$의 subset의 크기는 $4k\Delta’ \le 4k \frac{\delta}{4g} = \frac{\delta k}{g}$ 이하입니다. $L(t)$에서 $m$의 nonzero entry에 해당하는 subset $S$를 잡으면 $G(t)$가 lossless expander이므로 $\lvert N(S) \rvert \ge (1-\epsilon)g\lvert S \rvert > g\lvert S \rvert/2$이고, 따라서 $N(S)$에는 $S$의 한 vertex $u$와만 인접한 vertex $v$가 존재합니다. 그러면 $m_1 = A(t)m$의 $v$번째 엔트리는 $m$의 $u$번째 entry와 같을 수밖에 없고, 따라서 nonzero입니다. 그러므로 $m_1 \neq 0$.

$E_C^{t-1}$가 constant relative distance $\Delta$를 가지므로, $c_1 = E_C^{t-1}$의 weight은 최소 $2k \Delta \ge 2k \Delta’$ 입니다. 만약 $m$과 $c_1$의 weight의 합이 $4k \Delta’$ 이상이면 Claim의 조건을 만족했으므로 OK입니다. 그렇지 않은 경우, $c_1$의 nonzero entry에 해당하는 $G(t+1)$의 subset $S_1$의 크기는 $2k \Delta$ 이상 $4k \Delta’ \le \frac{\delta k}{g}$ 이하이고, $G(t+1)$가 lossless expander이므로 expand property를 만족하게 됩니다. 따라서 $\lvert N(S_1) \rvert \ge (1-\epsilon)g \lvert S_1 \rvert$이고, $N(S_1)$에서 $S_1$ 중 하나의 vertex와만 이웃한 vertex의 개수는 최소 $(1-2\epsilon)g \lvert S_1 \rvert \ge (1-2\epsilon)g \cdot 2k\Delta \ge \frac{1}{2}g \cdot 2k\Delta \ge 2k\Delta’$가 됩니다. 앞서 $m_1 \neq 0$임을 보일때와 같은 논리로 이는 $c_2 = A(t+1)c_1$의 weight의 하한이 되므로, $m, c_1, c_2$의 weight의 합은 $4k\Delta’$ 이상입니다.

따라서 Claim이 성립하고, 이에 따라 재귀적으로 정의된 Encoding $E_C^t$는 constant relative distance $\frac{\delta}{4g}$를 가집니다. $\blacksquare$

Testing Algorithm for Lossless Expander

위에서 본 바와 같이, 각각의 $t$에 대해 $\lvert L \rvert = 2^t, \lvert R \rvert = 2^{t-1}$인 Lossless Expander가 있다면 linear code인 Generalized Spielman code를 만들 수 있습니다. 이 때 lossless expander의 $g$는 constant이므로 인코딩 과정은 Linear time에 이루어지게 됩니다. 즉, Lossless expander를 미리 구해놓을 수 있다면 Linear time에 constant relative distance를 가지는 Linear code encoding을 할 수 있습니다.

그러면 이제 Linear-time encodable Linear code를 위해 남은 태스크는 Lossless Expander를 construct하는 것이 되겠습니다. Lossless Expander를 만드는 명시적인 방법이 예전부터 존재하지만([CRVW02]), 이는 practical한 알고리즘이라고 보기는 어렵습니다. 한편, 랜덤하게 생성된 bipartite graph는 높은 확률로 ($1 - O(\frac{1}{poly(k)})$) lossless expander가 됩니다.

다음 단락에서는 lossless expander를 sample하는 randomized algorithm에 대해 알아보도록 하겠습니다. 여기서는 problem solving에서 꽤나 알려진 문제가 사용됩니다.

Random Construction of Lossless Expander

Lemma 2([HLW06]). 정해진 $g, \epsilon, \delta$에 대해, random $g$-regular bipartite graph $G=(L,R,E)$은 $1 - O(\frac{1}{poly(k)})$ 확률로 $(k, k’; g)$-lossless expander이다.

그러나, 아쉽게도 위 Lemma의 $1 - O(\frac{1}{poly(k)})$는 negligible한 확률이라고 볼 수 없습니다.

한편, $(k, k’; g)$-lossless expander가 아닌 그래프를 sample할 확률은 크기가 $\log \log k$ 이하인 $S \in L$이 존재하여 expansion property( $N(S) \ge (1-\epsilon) g \lvert S \rvert$)를 만족하지 않는 경우에 dominate됩니다. 즉, sample하여 나온 그래프가 lossless expander가 아닌데 expansion property가 깨지는 크기 $\log \log k$ 이하의 subgraph가 없을 확률은 negligible합니다.

따라서, 크기 $\log \log k$ 이하의 모든 $S \subset L$에 대해 expansion property가 깨지는지를 체크할 수 있다면 random bipartite graph sampling으로 lossless expander를 construction할 수 있습니다 (negligible할 확률로 실패). 그리고 이를 체크하는 방법은 다음이 이용됩니다.

Definition(graph density). Undirected graph $G=(V,E)$가 있을 때, $V$의 부분집합 $S$에 대해 $S$로 induced되는 subgraph의 간선의 개수를 정점의 개수로 나눈 값을 해당 subgraph의 density $den(S)$라 한다. 그래프 $G$의 maximum density $Den(G)$는 모든 $S$에 대한 $den(S)$의 최댓값으로 정의한다.

Maximum density를 구하는 문제는 ICPC 문제([NEERC 2008 H])로도 출제된 적이 있는 문제입니다. maximum density로 가능한 값은 $O(N^2)$ 가지이고, 하나의 값을 정했을 때 그 값 이상의 density를 갖는 subgraph가 있는지를 MaxFlow 한번으로 판정할 수 있습니다. 따라서, maximum density subgraph는 $O(T_{maxflow} \log N)$ 시간에 구할 수 있습니다.

앞서 말씀드렸다시피, lossless expansion sampling을 위해 필요한 것은 size $\log \log k$ 이하의 subset에 대해 expansion property가 깨지는지를 체크하는 알고리즘입니다. Maximum density problem은 다음 Lemma에 의해 해당 알고리즘에 이용될 수 있습니다.

Lemma 3. 모든 $a \in L$의 degree가 $g$인 bipartite graph $G$가 모든 $L$의 부분집합에 대해 expansion property를 만족하는 경우 ($S$의 size의 upper bound가 없는 것과 동치), $Den(G)$는 $\frac{g}{1 + (1-\epsilon)g}$를 넘지 않는다. 그렇지 않다면, $Den(G)$는 $\frac{g}{1 + (1-\epsilon)g}$보다 크다.

이제 위 Lemma를 이용하여 Random bipartite graph에 대해 SUCCESS 또는 FAIL을 리턴하는 다음과 같은 알고리즘을 생각해봅시다.

Algorithm 2 (Distinguisher).

Setting

• constant $\delta, \epsilon, g$
• random bipartite graph $G = (L, R, E)$ with $deg(a) = g$ for every $a \in L$, $\lvert L \rvert = k$

Algorithm

1. $L$에서 $\lvert L’ \rvert = \delta k/g$를 만족하는 집합 $L’$을 random sampling한다.
2. $L’$로 induced된 subgraph $G’ = (L’, N(L’), E’)$의 maximum density $Den(G’)$를 구한다.
3. $Den(G’) > \frac{g}{1 + (1-\epsilon)g}$이면 FAIL을 리턴한다.
4. 앞서의 과정을 $(g/\delta)^{\log \log k}$ 번 반복한다.
5. FAIL이 return되지 않았다면 SUCCESS를 return한다.

알고리즘 Distinguisher는 다음을 만족합니다.

• $G$가 lossless expansion일 경우 ($\lvert S \rvert \le \delta k /g$를 만족하는 모든 $S \subset L$ 에 대해, $N(S) \ge (1-\epsilon) g \lvert S \rvert$), 1의 확률로 SUCCESS를 리턴
• $G$에 크기 $\log \log k$이하의 $S \subset L$이 존재하여 $N(S) <(1-\epsilon) g \lvert S \rvert$일 때, $\frac{1}{e}$ 이상의 확률로 FAIL을 리턴

그리고 앞서 보았듯이 두 가지 경우에 모두 포함되지 않을 확률은 negligible합니다.

Lossless expansion일 때 SUCCESS를 리턴하는 것은 Lemma 3에 의해 자명합니다. 그리고 샘플링한 $L’$이 $S$를 포함할 때 Lemma 3에 의해 FAIL이 리턴됩니다.

Distinguisher를 여러번 적용하여 Distinguisher가 모두 SUCCESS를 리턴했을 때 lossless expansion이 아닐 확률을 negligible하게 할 수 있으므로, Distinguisher를 이용하여 lossless expansion을 sampling할 수 있습니다. 즉, negligible한 확률로 실패하는 lossless expansion sampling 알고리즘이 완성되었습니다.

Running time을 보면, $(g/\delta)^{\log \log k}$ 는 $O(\log k)$ scale이므로 Distinguisher는 Maximum density algorithm을 $O(\log k)$번 실행하는 빠른 시간내에 작동합니다.

Linear-time Encodable Linear Code with Constant Relative Distance

지금까지 살펴본 내용으로, 아래와 같은 스텝을 거쳐 Linear-time Encodable Linear Code with Constant Relative Distance의 encoding scheme을 얻을 수 있습니다.

1. 상수 $g, \epsilon, \delta$를 정한다.
2. 필요한 모든 $t$에 대해, 2번 step을 통해 $\lvert L \rvert = 2^t, \lvert R \rvert = 2^{t-1}$인 lossless expander를 얻는다. (negligible한 확률로 실패)
3. Random bipartite graph를 생성하고, Distinguisher를 $\lambda$번 실행하여 모두 통과할 때까지 이를 반복한다.
4. Algorithm 1의 $E_C^t$를 얻는다.

Usage of Error Correcting Code

이때까지 Linear-time Encodable Linear Code를 어떻게 만드는지 알아보았습니다. 이런 Code는 통신시에 발생하는 Error를 Correcting할 때만 사용될까요?

Zero-Knowledge Proof에서 이러한 code를 사용할 수 있습니다. 그리고 이 때는 Linear time에 Encoding을 할 수 있다는 점이 굉장히 큰 이점으로 작용할 수 있습니다. 그러면 이제 어떤식으로 적용될 수 있을 지 알아봅시다.

polynomial commitment scheme

modern SNARK은 보통 polynomial commitment scheme과 polynomial IOP(Interactive Oracle Proof)로 이루어집니다. 이 중 polynomial commitment scheme은 commmit phase와 eval phase로 이루어집니다.

먼저, commit phase에서는 Prover가 polynomial $f$을 commit합니다. 즉, $f$에 대한 commit $com_f$를 public하게 공개합니다.

eval phase는 verifier가 $a \in \mathbb{F_p}$ 하나를 골라 Prover에게 $f(a)$의 값과 그것이 올바르다는 증거를 받고 verify하는 phase입니다.

polynomial commitment scheme에서는 $f$를 알고 있는 Honest prover는 항상 Accept되어야 하고, 그렇지 않은 prover가 통과할 확률은 negligible해야 합니다.

간단한 polynomial commitment scheme의 예시를 하나 들어보겠습니다. $F_p$에서 정의된 polynomial $f$를 생각해 봅시다.

처음에 Prover가 $f(0), \cdots f(p-1)$의 값을 leaf로 하는 Merkle Tree를 계산하여 root의 값을 commit합니다.

그 뒤 Verifier가 $f(a)$의 값을 물어보면, $f(a)$의 값이 있는 leaf로부터 root까지의 path에 있는 노드들과 그 자식 노드들의 값을 reveal합니다. Merkle Tree를 구성하는 Hash function의 충돌쌍을 찾지 못한다고 할 때, Honest prover가 아닌 경우 polynomial time에 verifier를 통과할 수 없습니다.

이 polynomial commitment scheme은 Prover가 모든 $\mathbb{F_p}$의 원소에 대해 $f$를 evaluate해야하기 때문에 practical한 용도로는 적합하지 않습니다. Polynomial commitment scheme에서 Prover의 계산량은 eval 호출에 대해 $f(a)$를 계산할 때 적어도 $f$의 degree $d$번의 field multiplication이 필요하고, 따라서 optimally $O(d)$가 됩니다.

오늘 소개드린 Linear-time Encodable Linear Code를 이용하여 optimal한 prover time $O(d)$를 가지는 polynomial commitment scheme을 구축할 수 있습니다. Reed-solomon과 같이 인코딩에 $O(d \log d)$ 시간이 걸리는 code를 사용하면 prover time이 $O(d \log d)$가 되기 때문에, 소개드린 Generalized Spielman code의 적용이 여기서는 큰 이점을 지니게 됩니다.

Conclusion

ZKP 관련 논문을 먼저 찾아보다가 Error correcting code를 통한 polynomial commitment scheme이 존재한다는 사실을 알게 되었고, 이 중 인코딩에서 graph theory가 사용되는 신기한 방법을 발견하여 소개하게 되었습니다. 이에 대해 설명하다 보니 정작 이것이 ZKP에서 어떻게 구현되는지에 대해서는 설명하지 못한 것이 약간 아쉽습니다.

error correcting code를 이용한 polynomial commitment scheme과 zero knowledge argument가 정확히 어떻게 이루어지는지에 대해서는 Linear code를 통해 Linear(Optimal) prover time과 poly-log proof size를 가지는 scheme을 제시한 Orion (논문 링크)에 자세히 나와 있습니다. 많은 배경지식이 없어도 이해할 수 있게 자세히 적혀 있으므로 Error correcting code를 이용한 ZKP에 흥미가 있다면 한번 읽어보는 것을 추천드립니다.

Reference

• Tiancheng Xie, Yupeng Zhang, and Dawn Song. “Orion: Zero Knowledge Proof with Linear Prover Time” (2022)
• [DI14] Erez Druk and Yuval Ishai. “Linear-time encodable codes meeting the Gilbert-Varshamov bound and their cryptographic applications. (2014)”
• [HLW06] Shlomo Hoory, Nathan Linial, and Avi Wigderson. “Expander graphs and their applications” (2006)
• [CRVW02] Michael Capalbo, Omer Reingold, Salil Vadhan, and Avi Wigderson. “Randomness conductors and constant-degree lossless expanders” (2002)