A Near-Optimal Deterministic Distributed Synchronizer
Synchronized message-passing model
분산 컴퓨팅 네트워크를 undirected graph $G=(V,E)$ 로 표현하자. 각 Node는 하나의 컴퓨터 또는 프로세서의 역할을 한다. Synchronized setting에서 계산 및 커뮤니케이션은 synchronous round에 이루어진다. 각 라운드마다 각 노드는 가지고 있는 데이터로 계산을 한 후 neighbor에 하나의 메시지를 보낼 수 있고, 이 때 보낼 수 있는 메시지의 크기에 따라 두 가지 모델로 나뉜다.
- CONGEST 모델: 보낼 수 있는 메시지의 크기를 $O(\log N) = B$ bit로 가정
- LOCAL 모델: 메시지의 크기에 제한을 두지 않음
보낸 메시지가 다 도착한 후 다음 round가 시작한다고 가정한다.
시작할 때 각 노드는 전체적인 $G$를 모르고, 자신의 identifier(노드 번호) 및 neighbor만 아는 상태이다.
Asynchronized Setting
이제 Asynchronous 세팅으로 바꾸어보자. 각 메시지가 send한 후부터 receive할 때 까지의 시간이 정해져 있지 않고, 알고리즘을 알고 있는 Adversary가 이를 정한다는 세팅이다. 즉 worst-case를 가정한다. 그런데 만약 Adversary가 임의로 전달 시간을 늘릴 수 있다면, “$n^{m!}$만큼 시간을 걸리게 하면 상상할 수 없을 정도로 느려지는거 아닌가?” 같은 생각이 떠오른다.
이에 Asynchronized setting에서는 각 node들이 모르는 메시지의 전달시간의 upper bound $\tau$ 가 있다 가정하고, 최종적으로 걸리는 시간 $T$를 $\tau$로 나눈 값을 Time complexity로 정의한다. Time complexity와 비슷한 개념으로 Message complexity 역시 정의할 수 있다. 이는 모든 Node의 메시지의 합의 asymptotic notation이다. Synchronous setting에서 이에 대응되는 내용으로는 총 communication round의 수를 Time complexity로 정의하고, Message complexity는 Asynchronous와 동일하게 정의한다.
Async 모델에서 각 edge가 메시지를 전달하는 동안 그 edge는 이용하지 못한다고 가정한다. 즉, 정점 $u$에서 neighbor $v$로 메시지를 시각 $b$ 에 보내서 $e$에 전달이 되었다고 하면 $u$는 $v$로 시각 $e$까지 다른 메시지를 send할 수 없다.
이 글에서는 “A Near-Optimal Deterministic Distributed Synchronizer” 논문에서 발표한 결과를 다룬다. Synchronous setting에서 시간복잡도 $T$와 메시지 복잡도 $M$을 가지는 algorithm이 있을 때, Asynchronous setting에서 $T \cdot$ poly($\log n$)의 시간복잡도와 $(M + m) \cdot$ poly($\log n$)의 메시지 복잡도를 갖는 알고리즘이 존재한다, 즉 둘 모두 poly($\log n$)의 overhead로 충분하다는 것이 결론이다.
논문의 내용이 상당히 복잡하기 때문에 최종 결론까지 이 글에서 모두 도출하지는 못했지만, 이에 사용된 아이디어와 개념들에 대해 최대한 자세하게 다루려고 노력하였다.
Multi-source BFS problem
분산 컴퓨팅 네트워크에서 간단하게 생각해볼 수 있는 대표적인 문제로는 Multi-source BFS problem이 있다. Multi-source BFS problem을 해결하는 알고리즘 $\mathcal{A}$가 있을 떄, 알고리즘 $\mathcal{A}$가 종료된 후 각 노드 $v$는 다음과 같은 정보를 가지고 있어야 한다.
- source들로부터의 최단거리 $dist(S, v)$ ($S$는 source 정점들의 집합)
- source가 아닌 경우, BFS Tree (shortest path tree)에서의 parent
Multi-source BFS problem을 synchronous setting에서 풀기는 간단하다.
- initialization : $v \in S$ 각각에 처음에 $dist(S,v) = 0$ 임을 저장한다.
- 각 round마다, distance가 새로 저장된 $v$ 들은 neighbor로 message $dist(S,v)+1$ 를 보낸다
- 처음으로 message가 온 node $v$는 sender를 BFS tree의 partner로 하고, message로 온 값을 $dist(S,v)$로 설정한다.
최종 시간복잡도는 $O(maxdist)$ 이다. 즉, $S$로부터 가장 먼 정점까지의 거리이다. 총 메시지의 개수는 $O(m)$이다. 이는 직관적으로 optimal 해 보인다.
그러나, Asynchronous setting에서는 distance가 더 큰 정점으로부터 온 메시지가 더 빨리 도착할 수 있고, 그러면 같은 알고리즘으로 틀린 답을 얻게 될 것이다.
Synchronous하면 간단하게 풀릴 문제가 순서가 꼬임으로서 복잡해졌기때문에 이를 바로잡고자 하는 것은 당연한 수순이다. 즉, $S$로부터 distance $k$인 정점이 보낸 메시지들이 다 도착한 후에 $S$로부터 distance $k+1$인 정점들이 메시지를 보내게 하고 싶다 (시간복잡도 및 메시지 복잡도를 크게 증가시키지 않으면서).
그런데 위 요구 조건은 distributed & asynchronous 세팅에서는 약간 “Global”하다. Global한 정보가 필요하면 먼 거리까지 정보가 전달되어야 하고, 그러면 Time complexity가 $O(n)$ factor를 포함하게 되는 원치 않는 결과가 된다 (뒤에 나오는 $\alpha$-synchronizer가 그 예시이다).
그래서 등장한 것이 “sparse cover”이다.
Sparse d-cover
양의 정수 $d$에 대해, sparse $d$-cover with stretch $s$는 다음과 같은 조건의 cluster들의 집합이다.
- 각 cluster $C$는 $V$의 부분집합
- 각 cluster의 diameter, 즉 가장 거리가 먼 두 node 사이의 거리는 $O(d \cdot s)$
- 각 node는 $O(\log n)$개의 cluster에 포함
- 각 node $u$에 대해, $u$와의 거리가 $d$ 이하인 임의의 $v$ 에 대해 $u,v$를 모두 포함하는 cluster가 존재
NOTE: cluster는 일반적으로 connected가 아니다.
각 node는 자신이 어떤 cluster에 속하는지 알고있으며, 또한 각 cluster $C$ 에 대해 cluster를 span하는 tree $T(C)$ 가 계산되어 ($T(C)$는 $G$의 subgraph) 이를 $C$의 steiner tree 라 한다. $C$의 각 node는 $T(C)$ 내에서의 parent/child를 알고있다.
우리가 사용할 cluster는 다음 조건들을 추가적으로 만족한다:
- cluster stretch는 $O(\log^3 n )$이다. 즉, 각 cluster의 steiner tree는 $O(d \log^3 n)$ 의 radius를 가진다.
- 각 edge는 최대 $O(\log^4 n)$ 개의 cluster steiner tree에 포함된다.
cluster stretch는 optimal value $O(\log n)$ 를 가지지만, 위 조건의 cluster가 distributed / asyncrhonous 세팅에서 compute가 효율적으로 가능함이 알려져 있다.
즉
- 시작할 때 각 노드는 전체적인 $G$를 모르고, 자신의 identifier(노드 번호) 및 neighbor만 알고 있음.
의 노베이스 상태에서 위 sparse cover를 계산할 수 있다는 것이다. 이를 어떻게 계산하는지는 뒤에서 자세히 다룬다.
Asynchronous Multi-source BFS
$2^t$-thresholded BFS, given a layered sparse $2^{t+6}$-cover
Definition(Layered sparse cover). $i = 1, 2, \cdots t$ 각각에 대한 sparsed $2^i$-cover를 가지고 있을 때 이를 layered sparse $2^{t}$-cover 라 한다.
Definition(Thresholded BFS). $d$-thresholded BFS problem을 해결하는 알고리즘에 대해, 알고리즘이 종료된 후 각 node $v$는 $dist(v, S)$가 $d$ 이하일 경우 $dist(v, S)$와 shortest path tree의 parent를, 아니면 $\infty$를 들고 있어야 한다.
이 때, 논문에서 다음이 성립함을 증명하였다:
Theorem 1. layered sparse $2^{t+6}$-cover가 주어졌을 때, $2^t$-thresholded multi-source BFS를 $O(2^t \log^8 n)$ time 과 $O(m \log^5 n)$ message complexity에 해결할 수 있다.
Theorem 1의 알고리즘에서 사용하는 아이디어를 아주 개략적으로만 설명하고 넘어갈 것이다. synchronous setting의 BFS는 다음과 같이 구현될 수 있다:
- pulse는 $0$부터 하나씩 증가하는 값이다.
- pulse $p$ 에서, source로부터의 distance가 $p$인 node들은 neighbor에게 “join” 메시지를 보낸다.
- 각 node는 자신이 처음으로 받은 join만을 accept하고, 메시지가 온 node를 parent로 둔다.
Asynchronous setting에서도 위의 방법을 사용하는데, 메시지가 asynchronous해도 $pulse(v)$가 source로부터의 거리임이 보장되도록 하기 위해 각 cluster별로 정보를 accumulate해서 각 pulse에 메시지를 보내도 된다는 신호를 cluster로부터 전달받으면 그때 메시지를 보낼 수 있도록 한다.
$2^t$-thresholded multi-source BFS와 마찬가지로, $2^t \cdot l$-thresholded multi-source BFS 역시 거의 동일한 방법으로 해결할 수 있다.
Theorem 2. layered sparse $2^{t+6}$-cover가 주어졌을 때, $2^t \cdot l$-thresholded multi-source BFS를 $O(2^tl \cdot \log^8 n)$ time 과 $O(ml \log^5 n)$ message complexity에 해결할 수 있다.
만약 layered sparse $2^{t+6}$-cover가 주어진 상테에서 sparse $2^{t+7}$-cover를 효율적으로 계산할 수 있다면, $t$를 1씩 증가시키면서 $2^t$-thresholded multi-source BFS를 asynchronous setting에서 할 수 있으므로 결국 multi-source BFS problem을 해결할 수 있게 된다.
Computing sparse cover
Synchronous setting에서 $O(d \log^{10} n)$ communication round로 다음 조건을 만족하는 sparse d-cover를 구성할 수 있음이 알려져 있다.
- cluster stretch는 $O(\log^3 n )$이다. 즉, 각 cluster의 steiner tree는 $O(d \log^3 n)$ 의 radius를 가진다.
- 각 edge는 최대 $O(\log^4 n)$ 개의 cluster steiner tree에 포함된다.
여기에 $\alpha$-synchronizer 를 사용하면 $O(d \log^{10} n)$ time과 $O(dm \log^{10} n)$ message complexity를 갖는 알고리즘이 된다.
$\alpha$-synchronizer
Synchronous setting의 알고리즘 $A$에 대해, 이를 Asynchronous setting에 적용하는 것을 생각하자. Asynchronous setting이 어려운 점 중 하나는 $u$에서 $v$로 보낸 메시지가 전달이 되었는지 여부를 $u$가 확인할 수 없다는 것이다. 이 문제는 $v$가 메시지를 전달받은 이후 전달받았음을 다시 $u$에게 알리는 메시지(Acknoweledge)를 보냄으로써 해결할 수 있다.
위 방식을 통해, Synchronous setting의 하나의 round가 Async setting에서 다음과 같이 이뤄질 수 있다.
- 각 노드에서, Sync setting에서 해당 round에 보내는 모든 메시지를 보냄
- 노드 $u$에서 $v$로 메시지를 보낼 때, $v$가 이를 받았음을 $u$가 확인하기 위해, $v$는 $u$에게 받았음을 확인하는 메시지를 send back (acknowledgement)
- 메시지를 보낸 모든 노드에 대해 답장을 받은 노드 $u$는 neighbor들에게 자신이 이번 라운드에 할 일이 끝났음을 전파
- 자신 및 자신의 모든 neighbor가 끝난 노드는 다음 round로 넘어감
위 synchronizer를 적용하면, 다음이 성립한다: Synchronous setting에서 $T(A)$의 communication round와 $M(A)$의 메시지 복잡도를 가지는 알고리즘 $A$에 대해, Asynchronous setting에서 $O(T(A))$의 시간복잡도와 $O(M(A) + m \cdot T(A))$의 메시지 복잡도를 가지는 알고리즘이 존재한다.
시간복잡도 측면에서 보면 이는 constant factor를 무시했을 때 optimal한 synchronizer이다. 그러나, 메시지 복잡도에 $m$ factor가 붙는다는 것은 치명적이라고 볼 수 있다.
이제 다시 Synchronous setting에서 $O(d \log^{10} n)$ communication round로 조건을 만족하는 sparse d-cover를 얻는 방법에 대해 알아보자.
k-separated Weak Diameter Network Decomposition
$G = (V,E)$에 대해, 상수 $\mathcal{C}$와 $\mathcal{D}$가 존재하여 다음이 성립한다고 하자.
- color의 집합 $1, 2, \cdots \mathcal{C}$에 대해, $G_1, G_2, \cdots G_{\mathcal{C}}$ 는 $G$의 vertex-disjoint partition.
- 각 $G_i$는 vertex-disjoint cluster $X_1, X_2, \cdots, X_l$ 로 이루어짐
- $X_a$의 임의의 두 정점 $u, v$에 대해, $G$에서의 $u, v$ 사이의 거리는 $\mathcal{D}$ 이하
- $a \neq b$ 일 때, 모든 $u \in X_a, v \in X_b$ 에 대해 $dist(u, v) > k$ 가 성립.
이 때 각 color에 해당하는 partition $G_i$ 들과 $G_i$를 구성하는 cluster들을 $G$의 k-separated Weak Diameter Network Decomposition 이라 한다.
Theorem 3(Rozhon and Ghaffari). 모든 Node에 대해 알려져 있는 값 $k$가 있을 때, $O(k \log^{10} n)$ communication round 안에 $(O(\log n),O(k \log^3 n))$ $k$-separated weak-diameter network decomposition of $G$를 계산하는 distributed synchronous algorithm이 존재한다. 이 알고리즘은 추가적으로 각 cluster에 대한 radius $O(k \log^3 n)$ steiner tree를 얻고, 이 때 $G$의 각 edge들은 최대 $O(\log^4 n)$번 사용된다.
즉, 위 알고리즘이 끝난 후 각 Node는 최종적으로 자신의 color $c$ 및 $G_c$ 내 자신이 들어있는 cluster $X_j$, 그리고 $X_j$의 steiner tree에서 자신과 인접한 정점들의 집합을 알고 있게 된다.
위 Theorem으로 $2d+1$-separated weak-diameter network decomposition을 계산했다고 하자. 각 cluster를 $d$-neighborhood까지 확장한 cluster들의 집합은 sparse $d$-cover가 되며 앞에서 추가적으로 말한 조건들도 만족한다. 각각의 항목을 체크해보면
- $G$에서 거리가 $d$ 이하인 $u, v$에 대해, 확장 전에 $u$를 포함했던 cluster는 확장 이후 $v$를 포함하게 되므로 모든 거리 $d$ 이하인 두 vertex $u, v$는 둘 모두를 포함하는 cluster가 존재하게 된다.
- 각각의 color에 대해 cluster들은 vertex disjoint하므로 각 노드는 최대 $O(\log n)$개의 cluster에 포함된다.
- $G$의 각 edge들은 expand하기 전에 최대 $O(\log^4 n)$개의 cluster steiner tree에 포함되었고, expand할 떄 color별로 최대 한 개의 tree에만 새로 포함될 수 있으므로 $O(\log^4 n)$개의 tree에 포함됨이 변하지 않는다.
- 각 steiner tree의 diameter 역시 $O(d \log^3 n)$ 임이 자명하다.
그런데 위와 같이 sparse $d$-cover를 만들면 $\alpha$-synchronizer 때문에 $O(m \cdot d \log^{10} n)$ 의 메시지 복잡도를 가지게 되는데, 우리가 synchronize에 사용하는 sparse $d$-cover는 $2^{1}$-cover, $2^2$-cover, $\cdots 2^t$-cover 가 모두 필요하며 $2^t$는 $O(n)$ scale이다. 이 sparse $d$-cover들을 모두 위 방식으로 만들면 $\tilde{O}(nm)$ 의, naive synchronous algorithm에 $\alpha$-synchronizer를 붙인 것보다 모든 면에서 좋지 못한 알고리즘이 된다.
다행히도, 처음 몇 개의 상수 크기의 $d$-cover만 위 방법으로 $O(m \log^{10} n)$ 의 메시지 복잡도로 생성한 후, 그 뒤의 sparse $2^i$-cover는 $2^{i-1}, 2^{i-2}, \cdots$ sparse cover들을 통해서 생성하는 효율적인 asynchronous algorithm이 존재한다. 그에 대해 알기 위해서는 앞서 설명한 $k$-separated weak-diameter network decomposition of $G$를 계산하는 알고리즘에 대해 좀더 자세히 살펴보아야 한다.
Lemma 1. 그래프 $G = (V, E)$와 $S \subset V$ 에 대해, 다음을 만족하는 $S’ \subset S$ 를 찾는 $O(k \log^9 n)$ commmunication round synchronous algorithm이 존재한다.
- $\lvert S \rvert \le 2 \lvert S’ \rvert$
- $S’$ 는 cluster $Y_1, Y_2 \cdots$ 의 disjoint union으로 표현되며, 이 때 다음 두 가지 조건이 성립한다.
- 각 cluster $Y_i$의 diameter는 $O(k \cdot \log^3 n)$
- 서로 다른 두 cluster의 두 정점 사이 거리는 항상 $k$ 초과
Lemma 1이 성립하면 처음에 $S=V$로 시작하여 $S’$ 를 찾고 $S$에 다시 $S \setminus S’$ 를 대입하는 식으로 반복하면 $\log N$ 번 만에 $S$는 공집합이 된다. 그동안 나온 $S’$들을 각각 $G_1, \cdots G_{\mathcal{C}}$로 놓으면 $G$의 $k$-separated weak-diameter network decomposition 이 됨은 자명하다.
이제 Lemma 1에서 실제로 사용되는 알고리즘에 대해 살펴보자. Lemma 1의 알고리즘은 $b = O(\log n)$개의 phase $0, 1, \cdots b-1$ 로 이루어진다. 처음에 $S$의 각 node $v$에 $b$-bit의 unique label $L(v)$를 부여하자. 이 label은 phase 중간중간에 바뀔 수 있다. 각 node는 alive 또는 dead 상태를 상태를 가지며, 처음에는 모두 alive 상태이다. $i$번째 phase의 시작 시점에서 alive 상태인 정점들의 집합을 $S_i’$라 하고, 그 중 길이 $i$의 bitstring $s$에 대해 label이 $s$를 suffix로 가지는 정점들의 집합을 $S_i’(s)$라 하자. phase $b-1$가 끝난 후에 alive인 정점들의 집합을 $S_b’$라 두면 $S = S_0’, S’ = S_{b}’$가 성립한다.
알고리즘이 시행될 때, 모든 $i$에 대해 $i$번째 phase의 시작 시점에 각 $S_i’(s)$ 들은 위에서 제시한 $S’$의 cluster 조건들을 만족한다. 즉 $S_i’(s)$ 내 정점들의 distance는 $O(k \cdot \log^3 n)$이며, 서로 다른 $s_1, s_2$에 대해 $S_i’(s_1), S_i’(s_2)$에서 정점을 하나씩 고르면 거리가 $k$ 초과이다. 어떤 과정으로 이 성질을 지키면서 각 phase가 시행되는지 살펴보자.
$i$번째 phase는 다음과 같이 이루어진다:
alive인 각 정점에 대해, 뒤에서부터 $i+1$번째 비트가 0인 정점들을 blue로, 1인 정점들을 red로 칠하자. blue인 모든 정점을 source로하는 $k$-threshold multisource BFS를 시행하여 shortest path tree를 얻었다고 하자 (synchornous algorithm이므로 간단히 해결된다). 이 때 $S_i’(1s)$ 에 포함되는 red node가 방문이 되었다면, $S_i’(0s)$에 포함되는 blue node로부터 방문이 된 것임을 알 수 있다(같은 $S_i’(s)$에 포함되어야 거리가 $k$ 이하). 모든 공집합이 아닌 $S_i’(0s)$에 대해, 다음을 시행한다:
- $S_i’(1s)$ 중 $k$-threshold multisource BFS 에서 방문된 점이 $\lvert S_i’(0s) \rvert/2b$ 개 미만이면, 해당 점들을 dead 상태로 만들고 $S_i’(0s)$ 에 대해서는 이후 step을 진행하지 않는다.
- $S_i’(1s)$ 중 $k$-threshold multisource BFS 에서 방문된 점이 $\lvert S_i’(0s) \rvert/2b$개 이상이면, 해당 점들의 label의 $1$을 $0$으로 바꾸어 suffix를 $0s$로 만들고 (blue node가 된다), shortest path tree의 간선들을 cluster tree에 추가한다. 만약 step이 멈추지 않은 blue node가 있다면, 해당 blue node들에 대해 다시 k-threshold multisource BFS를 진행하여 같은 방식으로 blue node set들을 확장해나가기를 반복한다.
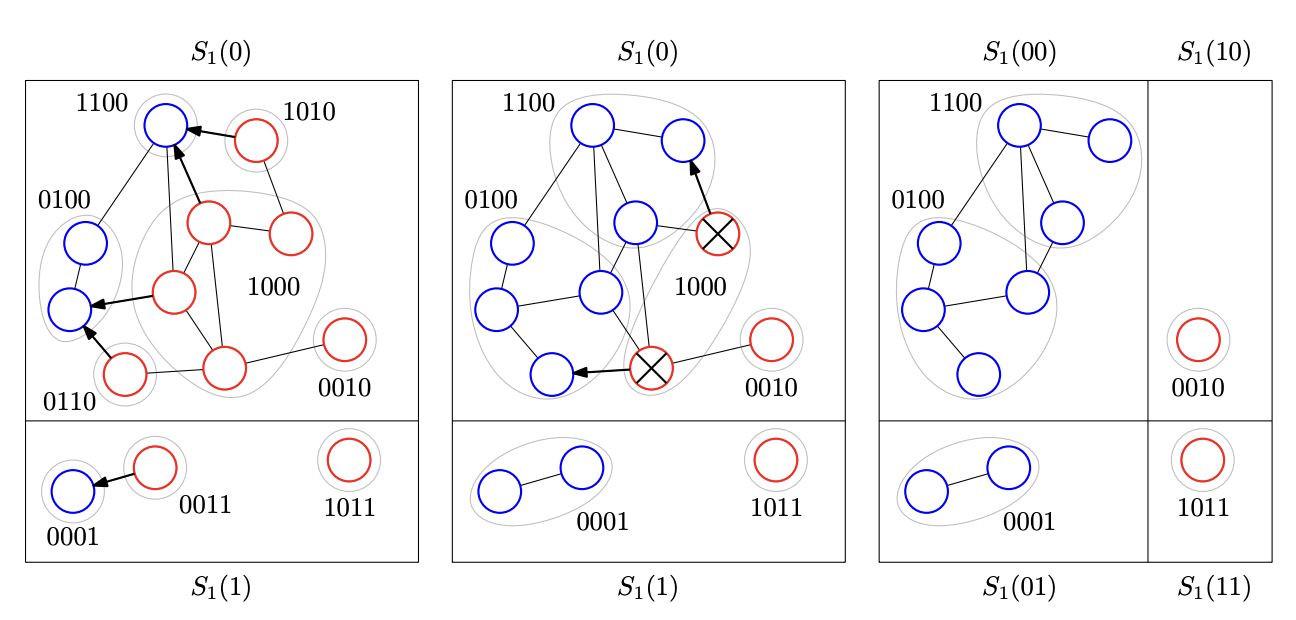
Figure 1. all steps of phase 1
위는 1번째 phase의 시작부터 step 2번이 진행되어 종료되기까지를 나타낸 그림이다.
만약 처음의 $S_i’(0s)$ 에 대해 step이 $t$번 진행되고 종료했다면 최종적으로 $\lvert S_{i+1}’(0s) \rvert / \lvert S_i’(0s) \rvert$는 $(1+1/2b)^t$ 이 상이므로, 이는 $2b \cdot \log n$을 넘을 수 없다. 따라서, 하나의 phase는 $2b \cdot \log n = O(\log^2 n)$ step 안에 종료하게 된다.
최종적으로 얻은 각 cluster는 BFS가 한번 실행될 때마다 diameter가 최대 $O(k)$만큼 늘어나므로, $b = O(\log n)$ 번의 phase동안 최대 diameter $O(k \log^3 n)$ 을 가지게 되므로 조건을 만족함을 확인할 수 있다. 그리고 blue cluster는 expand하거나 아니면 거리 $k$ 이하인 red node를 모두 dead시키므로, 서로 다른 cluster 사이의 거리는 최소 $k+1$ 이상이다.
각각의 step에서 blue cluster $S_i’(0s)$가 확장할지 말지를 결정하기 위해 red node가 몇개 방문되었는지를 accumulate해야 하며, 이는 cluster tree의 depth인 $O(k \log^3 n)$ round가 소모된다. 따라서 각 step은 $O(k \log^3 n)$ round에 구현될 수 있고, 그러면 최종적인 communication round는 $O(k \log^6 n)$이어야 할 것이다. 그런데 처음에 알고리즘에서 소개했던 communication round는 $O(k \log^9 n)$으로 로그가 3개나 더 붙어있다. 그 이유는 무엇일까?
처음에 CONGEST와 LOCAL 모델에 대해 소개했고, 용량이 무제한인 LOCAL 모델의 경우에는 $O(k \log^6 n)$ round만 필요한 것이 사실이다. 그러나, 각 edge들은 여러 steiner tree에 포함될 수 있다. dead node와 연결된 edge들도 steiner tree의 확장에서 얼마든지 쓰일 수 있음을 생각하면, 총 $O(\log^3 n)$ 번의 step이 존재하므로 각 edge는 최대 $O(\log^3 n)$ 개의 steiner tree에 포함될 수 있다. 그로 인해 CONGEST 모델에서는 추가적인 log factor가 3개 붙게 된다.
이제 다시 asynchronous setting에서 layered $2^{t+6}$ sparse cover가 주어졌을 때, $\alpha$-syncrhonizer 없이 sparse $2^{t+7}$-cover를 구하는 방법을 생각해 보자. 이는 사실 synchronous 세팅에서 사용한 방법을 거의 그대로 적용하면 된다. $2 \cdot 2^{t+7}+1$-separated weak-diameter network decomposition을 계산하면 충분한데, synchronous algorithm에서 하듯이 하면 각 step에서 필요한 연산은 $d$-threshold BFS($d = 2 \cdot 2^{t+7}+1$) 및 red node 개수를 세서 blue cluster를 expand할지 결정하는 것이다. 그런데 thresholded BFS는 Theorem 2에 의해 asynchronous setting에서 가능하므고, red node를 카운팅하는 것도 cluster의 diameter가 $O(k \log^3 n)$임을 이용하면 asynchronous setting에서도 어렵지 않게 가능하다.
Polylogarithmic synchronizer
Multi-source BFS 문제는 사실 layered sparse cover를 만드는 데에 사용되고, 또 layered sparse cover를 이용해 Multi-source BFS를 해결하므로 sparse cover와 함께 기본적인 building block으로 사용되는 알고리즘이라고 볼 수 있다.
Layered sparse cover가 주어져 있을때 thresholded multi-source BFS 문제는 결국 pulse $p-1$의 메시지 전달이 모두 완료된 후 pulse $p$의 메시지를 보내도록 하는 것을 보장하여 해결이 되었는데, 이는 결국 일반적인 synchronous algorithm에서 round의 개념이 보장되도록 하는 것이 poly($\log n$)의 overhead로 가능함을 보인 것이다. 따라서, 결국 multi-source BFS 문제를 해결하듯 일반적인 synchronous algorithm역시 poly($\log n$) overhead로 asynchronous setting에서도 synchronous인 것처럼 해결할 수 있다.
Reference
- Mohsen Ghaffari, Anton Trygub. “A Near-Optimal Deterministic Distributed Synchronizer” (2023)
- Václav Rozhoň, Mohsen Ghaffari. “Polylogarithmic-Time Deterministic Network Decomposition and Distributed Derandomization” (2019)