Erdös-Ginzburg-Ziv 정리의 O(n log n) 시간 해법 찾기
Erdös-Ginzburg-Ziv 정리는 임의의 길이 $2n-1$의 정수열에 대해 길이가 $n$이고 원소의 합이 $n$의 배수인 부분수열이 항상 존재한다는 정리입니다. 이전에 작성된 글에서는 $O(n^2/w)$ 풀이를 소개했지만, 최근에 공개된 이 부분수열을 직접 찾는 $\mathcal{O}(n \log n)$ 풀이에 대해서 소개합니다.
Erdös-Ginzburg-Ziv 정리와 증명
Erdös-Ginzburg-Ziv 정리는 길이가 $2n-1$인 임의의 정수열 $A = { {a}_1, {a}_2, \cdots, {a}_{2n-1}}$에 대해 길이가 $n$이고 원소의 합이 $n$의 배수인 부분수열이 항상 존재한다는 정리입니다. $A$에 따른 $A$의 부분수열을 Erdös-Ginzburg-Ziv 정리의 해법이라고 부릅니다. Erdös-Ginzburg-Ziv가 간단한 증명을 제시했고, 이 증명을 재구성해서 작성해보면 다음과 같습니다.
이 증명에서는 강한 수학적 귀납법을 사용합니다. $n=1$일 때 참이고, $n=1, 2, \cdots, k-1$일 때 참인 결과로 $n=k$인 경우를 증명할 수 있으면, 우리는 모든 $n$에 대해서 해당 명제가 참이라는것을 증명할 수 있습니다. $n=1$일 때는 자명하기 때문에, $n \ge 2$인 경우 소수와 합성수로 나누어서 증명합니다.
$n=p$가 소수인 경우
$A = {a_1, \cdots, a_{2p-1}}$의 각 원소를 $p$ 로 나눈 나머지로 정렬한 수열을 $B = {b_1, \cdots, b_{2p-1}}$이라고 합시다. 이 수열에서 부분수열을 찾으면 순서를 잘 옮겨주는 것으로 $A$에서도 부분수열을 찾을 수 있기 때문에, $B$에서 문제를 해결하도록 하겠습니다.
$b_i \equiv b_{i+p} \pmod p$인 $i$가 존재하는 경우에는, $b_{i}, b_{i+1}, \cdots, b_{i+p-1}$가 $p$로 나눈 나머지가 같기 때문에, 합이 $p$의 배수가 됩니다. 이렇지 않은 경우에는 두 원소간의 차이인 $d_i = b_{i+p} - b_i$ $(1 \le i < p)$가 $p$의 배수가 아닙니다.
이제 부분수열 중에서 $b_i$와 $b_{i+p}$ $(1 \le i <p)$ 중에서 정확히 하나만 포함하는 부분수열만 생각할 것입니다. 각 $i = 1, \cdots, p-1$ 중 $b_i$와 $b_{i+p}$중 어느 하나를 고르게 되고, 나머지 하나의 원소는 $b_p$가 됩니다. 수식으로 작성하면, ${c_1, \cdots, c_p}$ 꼴의 부분수열만 생각하고, $c_j \in {b_j, b_{j+p}}$ $(1 \le j \le p-1)$ 이고, $c_p=b_p$입니다.
이제 동적계획법과 비슷한 아이디어를 사용합니다. ${c_1, \cdots, c_p}$ 꼴의 부분수열 중에서 $c_1 + \cdots + c_p$를 $p$로 나눈 나머지로 가능한 것을 생각할 것입니다. 여기서 추가적인 조건을 거는데, 우리는 수를 고르는 범위를 하나씩 늘려나갈것입니다. 구체적으로는, $S_i$ ($1 \le i \le p$) 를 $c_i = b_i, c_{i+1} = b_{i+1}, \cdots, c_p = b_p$ 를 모두 만족하는 (즉, $i$ 미만의 원소에만 선택지가 있는) 꼴에서 $c_1 +\cdots + c_p$를 $p$로 나눈 나머지로 가능한 것을 모두 모은 집합입니다.
이제, $S_i$에 대한 점화식을 만들어봅시다. $c_i$를 $c_{i+p}$로 합이 $c_{i+p} - c_i$만큼 늘어난다는 점을 착안합니다. $X \oplus_p Y = {(x+y) \bmod p \mid x \in X, y \in Y } $로 쓰면, $S_{i+1} =S_{i} \oplus_p {0, d_{i}}$ 라는 점을 알 수 있습니다.
Cauchy Davenport
이제, $\phi \neq S \subsetneq {0, 1, \cdots, p-1}, a \not \equiv 0 \pmod p$이면, $S \subsetneq S \oplus_p {0, a}$라는 것을 증명합시다. $S = S \oplus_p {0, a}$라면, $s \in S$ 에 대해 $s + a \in S \oplus_p {0, a} = S$여야 합니다. 즉, $s, s+a, s+2a, \cdots \in S$ 여야 합니다. $a$와 $p$가 서로소이기 때문에 ${s, s+a, s+2a, \cdots} = {0, 1, \cdots, p-1}$이고, 이는 가정의 $S \subsetneq {0, 1, \cdots, p-1}$과 모순입니다.
그래서 $S_i$의 크기가 $p$ 이하인 동안에는 계속 적어도 $1$씩 늘어나게 되기 때문에 $S_p$의 크기는 $p$가 됩니다. $\square$
$n = pq$가 합성수일 경우
$n=pq$이고, $p, q\ge 2$라고 합시다. 우리는 $2p-1$개의 수를 골라서 합이 $p$의 배수가 되게 할 수 있고, $2p-1$개를 골라서 합이 $q$의 배수가 되게 할 수 있다는, 강한 수학적 귀납법의 귀납 가정을 사용합니다.
총 $2pq-1$개의 수 중 $2p-1$개의 수를 뽑아서 그 중 $p$개의 합이 $p$의 배수가 되도록 할 수 있습니다. 이렇게 $p$개의 수를 제외하게 되면 $p(2q-1)-1$개의 수가 남게 됩니다. 이 수가 $2p-1$이상이면 수를 계속 뽑을 수 있습니다. 이렇게 뽑으면 $2q-1$개의 집합이 나오는데, $i$번째 집합은 $p$개의 수가 들어있고, 합이 $s_i$가 되도록 할 수 있습니다. (이는 $p$의 배수입니다.)
이제 $2q-1$개의 새 정수 $\dfrac{s_1}{p}, \dfrac{s_2}{p}, \cdots, \dfrac{s_{2q-1}}{p}$에 대해서 $q$에 대한 귀납가설을 써 줍니다. 이 중 $q$개의 수를 골라서 합이 $q$의 배수가 되도록 할 수 있습니다. $s_i$에 해당하는 $p$개의 수를 다시 써주면, $pq$개의 수를 골라서 합이 $pq$가 됩니다 $\square$
Erdös-Ginzburg-Ziv 정리의 해법 찾기
이제 이 증명을 이용해서 Erdös-Ginzburg-Ziv 정리의 해법을 찾아줄 것입니다. 증명처럼 소수일 때와 소수가 아닐 때를 나눠서 찾아줄 것입니다.
$n=p$가 소수인 경우
$S_i$라는 집합을 직접 관리하는 방식으로 문제를 해결하면 $\mathcal O(n^2)$ 혹은 $\mathcal O(n^2 / w)$ 시간 복잡도가 나옵니다. 이 방법보다 빠른 방법은 $S_i$의 부분집합 $T_i$를 관리하는 것입니다. 증명에서 $S_i$의 크기가 이전 집합보다 $1$씩 커진다는 점을 이용 했기 때문에, 우리는 새로 추가되는 전체 원소를 찾을 필요 없이 $1$씩 커지는 원소만 찾아주면 됩니다.
$T_1 = {b_1 + b_2 + \cdots + b_p}$이고, $T_{i} \oplus_p {d_{i}}$에서 $T_i$에 속하지 않는 원소 $t_i$를 하나 찾아서 $T_{i+1} = T_i \cup {t_i}$가 되도록 추가해줍니다. $S_{i+1} =S_{i} \oplus_p {0, d_{i}}$이기 때문에 $T_{i+1} \subset S_{i+1}$ 인것을 증명할 수 있습니다.
이제 이 $t_i$를 찾아봅시다. $b_1 + b_2 + \cdots + b_p \in T$에 대해서 계속 $d_i$를 더하면 어느 순간 $b_1 + b_2 + \cdots + b_p +xd_i \not \in T$인데 $b_1 + b_2 + \cdots + b_p +(x+1)d_i \not \in T$가 됩니다. 이렇게 되는 $x$를 찾으면, $t_i = b_1 + b_2 + \cdots + b_p +(x+1)d_i $가 $t_i$의 조건을 만족합니다.
Find_T
- $p, T_i, u \in T_i, v \not\in T_i$ 일 때, $T_i$에 추가되는 $t_i$를 반환합니다.
def Find_t(p, T, d, u, v):
l, h = u*pow(d, -1, p) % p, p+v*pow(d, -1, p) % p
while l+1 != h:
m = (l+h)//2
if T[m*d % p]:
l = m
else:
h = m
return h*d % p
$(l \times d_i) \bmod p$가 $T$의 원소이고, $(h \times d_i) \bmod p$가 $T$의 원소가 아니도록 $l, h$를 유지시켜 줍니다. 이 과정에서 $\lvert h-l \rvert$를 이분탐색과 비슷한 방식으로 줄여나갑니다. $m = \left\lfloor \frac{l+h}{2} \right\rfloor$ 를 잡고, $(m \times d_i) \bmod p$가 $T$에 속하는지 여부에 따라서 $h$혹은 $l$로 만들어줍니다.
최종적으로 while문을 빠져나오면, $l+1 = h, ((h-1) \times d_i) \bmod p \in T, (h \times d_i) \bmod p \in T$ 가 되브로, $(h \times d_i) \bmod p$를 반환해줍니다.
$T_i$ 관리
이제 $0 \not \in T_{i-1}$ 인 동안, $T_i$를 계속 만들어줍니다. 이 때, $t_i$가 추가된 내역은 트리 구조로 표현할 수 있습니다. $T_{i}$의 각 원소 $t$에 대해, 해당 $t$에 해당하는 $B$의 부분수열을 관리합니다. $T_i$에 $t_i$가 추가되었다는 뜻은, $t_i - d_i$에 해당하는 부분수열에서 $b_i$를 $b_{i+p}$로 바꾸면 된다는 의미입니다. 이런 바뀐 부분만 관리하는 트리 구조를 만들면 변화를 $\mathcal O(1)$에 추적할 수 있습니다.
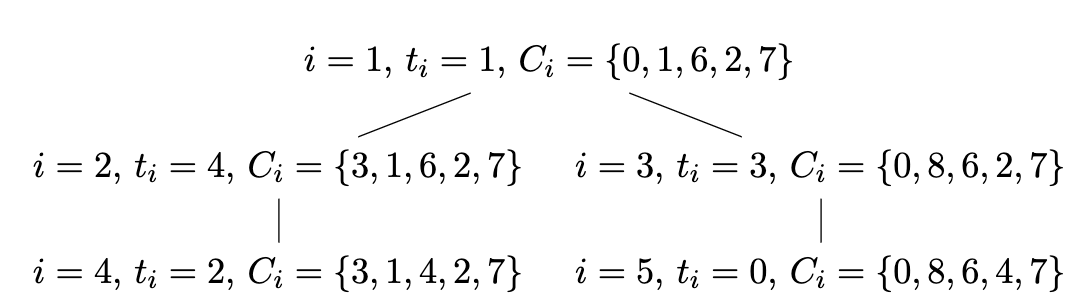 |
|---|
| $p = 5, B = {0, 1, 6, 2, 7, 3, 8, 4, 9}$ 일 때 트리 구조 예시 |
def EGZ_prime(p, a):
k = sorted(range(2*p-1), key=lambda x: a[x] % p)
L = [False] * (2*p-1)
for i in range(p-1):
if a[k[1+i]] % p == a[k[p+i]] % p:
for i in range(1+i, 1+p+i):
L[k[i]] = True
return L
s = sum((a[k[i]] for i in range(p))) % p
T, P = [False]*p, [None]*p
T[s] = True
for i in range(1, p):
if T[0]:
break
t = Find_t(p, T, (a[k[p+i-1]]-a[k[i]]) % p, s, 0)
T[t] = True
P[t] = i
c = 0
for i in range(p):
L[k[i]] = True
while s != c:
L[k[p+P[c]-1]], L[k[P[c]]] = True, False
c = (c - (a[k[p+P[c]-1]]-a[k[P[c]]])) % p
return L
$n=pq$가 합성수인 경우
증명 방식을 그대로 구현하면 됩니다.
def EGZ_composite(p, q, a):
S, T = list(range(p-1)), [None]*(2*q-1)
for i in range(2*q-1):
S.extend(range((i+1)*p-1, (i+2)*p-1))
ret = EGZ(p, [a[s] for s in S])
T[i] = [S[j] for j in range(2*p-1) if ret[j]]
S = [S[j] for j in range(2*p-1) if not ret[j]]
L = [False]*(2*p*q-1)
ret = EGZ(q, [sum(a[t] for t in T[i])//p for i in range(2*q-1)])
for i in range(2*q-1):
if ret[i]:
for j in T[i]:
L[j] = True
return L
def EGZ(n, a):
if n == 1:
return [True]
for i in range(2, n):
if n % i == 0:
return EGZ_composite(i, n//i, a)
return EGZ_prime(n, a)
이 방법으로 Erdös-Ginzburg-Ziv 정리의 해법을 $\mathcal O(n \log n)$ 시간에 찾을 수 있습니다.
결론
Erdös-Ginzburg-Ziv 정리의 해법을 $\mathcal O(n \log n)$ 시간에 찾는 방법에 대해 알아보았습니다. 수학 중에서도 정수론 문제에 대해서는 주로 구성론적인 해법이 많이 등장하는데, 이를 컴퓨터과학의 테크닉을 사용해서 탐색 공간 및 시간을 줄이는 방법을 사용하는 한 가지 예입니다. 다른 문제나 정리에 대해서도 해의 존재성 뿐만이 아니라, 실제로 해를 효율적으로 구성하는 방법에 관한 연구가 활발해 졌으면 좋겠습니다.