ainta's profile image

ainta

September 24, 2023 00:00

Introduction

2021년 Maximum Flow는 Almost-Linear Time에 풀린다는 결과가 발표되었다 (이는놀랍게도 Minimum cost Flow에 대해서도 성립하는 명제이다). 이에 관련하여 공부할 수 있는 자료로는 Rasmus Kyng의 Advanced Graph Algorithms and Optimization 강의가 있어 이에 대한 스터디를 진행하였다. 이 강의의 Chapter 17인 “Interior point mehods for maximum flow” 를 정리해서 소개하려고 한다. 17장에서는 16장까지 다루었던 테크닉을 통해 undirected graph의 maximum flow 문제를 $\tilde{O}(m^{1.5})$ 시간에 해결하는 알고리즘을 제시한다. 16장까지 많은 정보가 소개된 만큼, 이 글은 self-contained되지 않았다. 그러니 어떤 정보가 필요한지 먼저 소개한다.

Prerequisites

Laplacian

Graph $G$의 Laplacian은 그래프 이론에서 중요한 object이다. Laplacian의 determinant는 $G$의 스패닝 트리 개수와도 관계가 있고(키르히호프 정리), 또한 Laplacian의 eigenvalue는 그래프의 유의미한 지표로 사용된다.

Definition. 정점이 $n$개, 간선이 $m$개인 무방향 그래프 $G$의 Laplacian $L _ {G}$는 $D - A$로 정의된다. 여기서 $D$는 $D _ {i, i} = \deg(i)$를 만족하는 대각행렬이고, $A$는 $G$의 인접행렬이다.

정점 $n$개와 간선 $m$개를 가지는 그래프의 Laplacian $L$에 대해, linear equation $Lx=b$를 해결하는 문제는 markov chain에서 random walk의 hitting time 등 여러 문제에 사용될 수 있는 강력한 subproblem이다. 이에 대해, 다음과 같은 결과가 알려져 있다.

Theorem(Kyng, 2015). Laplacian $L$에 대해, Equation $Lx = b$의 approximation solution을 높은 확률로 $O(m \log^{3} n)$ 시간 안에 찾을 수 있다. (이에 대한 자세한 설명은 TAMREF님의 소프트웨어 멤버십 블로그 글을 참고하면 좋다)

Convex Optimization, Duality, Lagrangian, KKT Condition

위 개념들 또한 이 글을 이해하는데에 필수적으로 필요한 개념들이다. 이에 관해서는 같이 스터디를 진행한 koosaga님의 소프트웨어 멤버십 블로그 글을 읽어보는 것을 추천한다.

Notations

자주 사용되는 notation과 개념에 대해 Undirected Maximum Flow Problem을 통해 설명할 것이다.

\[\max_{f \in \mathbb{R}^m} F\] \[\text{s.t. } Bf = Fb_{st}\] \[-c \le f \le c\]

을 undirected maximum flow problem이라 한다.

여기서 각각이 symbol이 의미하는 바는 다음과 같다.

• $f$는 각 edge $(u,v)$의 flow이다. 음수이면 $v$에서 $u$로 흐른다는 뜻이다.
• $B$는 $m \times n$ matrix. Edge $e$ = $(u,v)$ 에 대해, $B_e$ 는 $v$ 에서 1, $u$에서 -1, 그 외에서 0이다.
• $b_{st} \in \mathbb{R}^n$ 는 source $s$ 에 -1, sink $t$ 에 1, 나머지가 0인 크기 $n$의 vector이다.
• $c \in \mathbb{R_{+}}^m$은 각 edge의 capacity이다.

앞으로 벡터 $f, c$에 대해서는 $f(e), c(e)$ 꼴로도 쓸 것이다. $f(e)$는 edge $e$의 flow, $c(e)$는 capacity이다.

Linearly Constrained Newton’s Method

아래와 같이 Linear constraint만 존재하는 convex optimization program을 생각하자. ($\mathcal{E}: \mathbb{R}^n \rightarrow \mathbb{R}$는 convex function)

\[min_{f \in \mathbb{R}^n} \mathcal{E}(f)\] \[\text{s.t. } Bf=d\]

Taylor 근사에 의해, $\mathcal{E}(f+\delta) \approx \mathcal{E}(f) + \langle \nabla\mathcal{E}(f), \delta \rangle + \frac{1}{2}\langle \delta, H_{\mathcal{E}}(f)\delta \rangle $ (단, $H_{\mathcal{E}}(f)$ 는 $\mathcal{E}$의 $f$에서의 Hessian)

위 식에 따라 Newton’s method로 $f$를 $f+\delta$로 update할 때, $\langle \nabla\mathcal{E}(f), \delta \rangle + \frac{1}{2}\langle \delta, H_{\mathcal{E}}(f)\delta \rangle $ 를 minimize한다. 단, $B(f+\delta) = d$ 역시 유지되어야 하므로 $B\delta = 0$ 이 constraint가 된다.

즉, Newton step $\delta^{\ast}$ 는 다음의 minimizer이다.

\[\min_{\delta \in \mathbb{R}^m, B\delta = 0} \langle \nabla\mathcal{E}(f), \delta \rangle + \frac{1}{2}\langle \delta, H_{\mathcal{E}}(f)\delta \rangle\]

$g = \nabla\mathcal{E}(f), H = H_{\mathcal{E}}(f)$ 으로 간략히 나타내면 이는

\[\min_{\delta \in \mathbb{R}^m, B\delta = 0} \langle g, \delta \rangle + \frac{1}{2}\langle \delta, H\delta \rangle\]

이고, 이는 Lagrangian $L(\delta, x) = \langle g, \delta \rangle + \frac{1}{2}\langle \delta, H\delta \rangle - x^TB\delta$ 를 가지므로 위 최솟값은

\[\max_{x\in\mathbb{R}^n}\min_{\delta\in\mathbb{R}^m} L(\delta, x) = \max_{x\in\mathbb{R}^n}\min_{\delta\in\mathbb{R}^m} \langle g, \delta \rangle + \frac{1}{2}\langle \delta, H\delta \rangle - x^TB\delta\]

와 같다. (Duality)

KKT Optimality condition은 아래와 같다.

• $B\delta = 0$
• $\nabla_\delta L(\delta, x) = g+H\delta - B^Tx = 0$

위 식의 양변에 $BH^{-1}$를 곱하면 $BH^{-1}g + B\delta - BH^{-1}B^Tx = 0$인데

$B\delta=0$이므로 $BH^{-1}g = BH^{-1}B^Tx$.

$L = BH^{-1}B^T$ 라 놓으면 $x = L^{-1}BH^{-1}g$

따라서, solution ($x^{\ast}, \delta^{\ast}$)는

• $x^{\ast} = L^{-1}BH^{-1}g$
• $\delta^{\ast} = H^{-1}(B^Tx^{\ast} - g)$ 이다. newton step $\delta^{\ast}$를 위와 같이 구할 수 있고, $f_{k+1} = f_k + \delta^{\ast}$로 update한다.

여기서 만약 $\mathcal{E}(f)$가 $\sum_e \mathcal{E}_i(f(e))$ 꼴이라면 Hessian이 Diagonal이므로 $L$은 Laplacian matrix가 되고, newton step $\delta^{\ast}$는 Laplacian solver를 통해 $\tilde{O}(m)$ 시간에 구할 수 있다.

Convergence given $K$-stable Hessian condition

Definition. $\mathcal{E}$에 대해 constant matrix $A$가 존재하여 $\frac{1}{1+K}A \le H_{\mathcal{E}}(y) \le (1+K)A$를 만족할 때, $\mathcal{E}$가 $K$-stable Hessian condition을 만족한다고 한다.

Linear constraint만 존재하는 convex optimization program에 대해 Newton mehtod의 Convergence에 대한 다음 정리가 성립한다. 이에 대한 증명은 생략한다.

Theorem. $H_{\mathcal{E}}(f)$가 $K$-stable Hessian일 때, 위 Newton method는 $(K+1)^6 \log(1/\epsilon)$ 번의 step 안에 approximation solution을 구한다. 즉, 모든 $f$에 대해 $\frac{1}{1+K}A \le H_{\mathcal{E}}(y) \le (1+K)A$ 를 만족하는 constant matrix $A$가 존재할 때, $\mathcal{E}(f_{k}) - \mathcal{E}(y^{\ast}) \le \epsilon( \mathcal{E}(f_{0}) - \mathcal{E}(y^{\ast}) )$ 가 성립한다.

즉,Linear constraint만 존재하는 convex optimization program이 다음 조건을 만족할 때,

• $K$-stable Hessian condition을 만족
• $\mathcal{E}(f)$가 $\sum_e \mathcal{E}_i(f(e))$ 꼴

log 번의 Laplacian equation solving으로 Approx solution을 구할 수 있다. 따라서, $\tilde{O}(m)$시간에 approximation solution을 구할 수 있다.

Interior Point Methods for Maximum Flow

Undirected Maximum Flow Problem

\[\max_{f \in \mathbb{R}^m} F\] \[\text{s.t. } Bf = Fb_{st}\] \[-c \le f \le c\]

위 undirected maximum flow problem을 생각하자.

Notation. maximum flow를 $F^{\ast}$ 라 하고, maximum flow $F^{\ast}$에 대해 위 식을 만족하는 flow 하나를 $f^{\ast}$ 라 하자.

Barrier Function

\[V(f) = \sum_e -\log(c(e) - f(e)) - \log(c(e) + f(e))\]

을 생각하자.

Intuition

• $V(f)$는 $\lvert f(e) \rvert$ 가 $c(e)$를 벗어나면 정의되지 않는다.
• $f(e) = 0$에서 최솟값을 가지며 $\lvert f(e) \rvert$가 $c(e)$에 매우 가까이 접근하면 엄청나게 커질 수 있는 함수이다.

\[\min_{f \in \mathbb{R}^m} V(f)\] \[\text{s.t. } Bf = \alpha F^{\ast}b_{st}\]

위 문제를 Barrier Problem이라 한다. 이 때 $\alpha$ 는 $0 \le \alpha < 1$을 만족하는 상수이다. Barrier Problem의 feasible solution은 당연히 $-c \le f \le c$ 를 만족함을 알 수 있다.

$\alpha f^{\ast}$ 는 $Bf = \alpha F^{\ast}b_{st}$ 를 만족하므로 위 problem의 feasible solution이고, 따라서 $V(\alpha f^{\ast}) < \infty$.

만약 $\alpha = 1-\epsilon$에 대한 위 program의 optimal flow를 찾는다면, 해당 flow는 undirected maximum flow problem에서 $F = \alpha F^{\ast} = (1-\epsilon)F^{\ast}$인 feasible solution이다. 따라서, 이는 undirected maximum flow problem의 $\epsilon$-approximation solution이 된다.

Barrier Problem은 Lagrangian $L(f,x) = V(f) + x^T(\alpha F^{\ast}b_{st} - Bf)$를 가진다.

Optimality condition은

• $Bf = \alpha F^{\ast}b_{st}$
• $-c \le f \le c$
• $\nabla_f L(f,x) = 0 \Rightarrow \nabla V(f) = B^Tx$

Notation. Barrier Problem에서 주어진 $\alpha$에 대해 optimal solution을 $f_\alpha^{\ast}$라 하고, 그 때의 dual voltage를 $x_\alpha^{\ast}$ 라 하자. 이 때 optimality condition에 의해 $\nabla V(f_\alpha^{\ast}) = B^Tx_\alpha^{\ast}$가 성립한다.

Updates using Divergence

Barrier Problem을 newton step을 통해 해결하고자 한다. 즉, $f_\alpha^{\ast}$ 가 있을 때 $f_{\alpha+\alpha’}^{\ast}$ 를 newton step $f_{next} = f + \delta$ 를 통해 구하는 방식으로 해결하고자 한다.

\[\min_{\delta \in \mathbb{R}^m} V(f+\delta)\] \[\text{s.t. } B\delta = \alpha' F^{\ast}b_{st}\]

를 Update Problem이라 하자.

$0 < \alpha’ < 1-\alpha$ 에 대해, Update problem의 optimal solution $\delta^{\ast}$을 구했다면 $f_\alpha^{\ast} + \delta^{\ast}$는 $\alpha + \alpha’$인 Barrier problem의 Optimal solution이 된다. ($B(f_\alpha^{\ast} + \delta^{\ast}) = (\alpha + \alpha’)F^{\ast}b_{st}$)

그런데 Update problem의 optimal solution을 찾는 것은 Barrier Problem을 푸는 것만큼이나 어려워 보인다. 이를 조금 변형해 다음과 같은 문제를 생각해보자.

\[\min_{\delta \in \mathbb{R}^m} V(f+\delta) - (V(f) + \langle \nabla V(f), \delta\rangle )\] \[\text{s.t. } B\delta = \alpha' F^{\ast}b_{st}\]

이를 Divergence Update Problem이라 한다.

Lemma. $f = f_\alpha^{\ast}$일 때, Divergence Update Problem의 optimal solution은 Update Problem의 optimal solution $\delta^{\ast}$과 동일하다.

Proof. Recall Barrier Problem의 Optimality Condition: $\nabla V(f_\alpha^{\ast}) = B^Tx_\alpha^{\ast}$

따라서, $B\delta = \alpha’ F^{\ast}b_{st}$ 를 만족하는 임의의 $\delta$에 대해 다음이 성립한다.

$\langle \nabla V(f_\alpha^{\ast}), \delta\rangle = \langle B^Tx_{\alpha}^{\ast}, \delta\rangle = \langle x_{\alpha}^{*}, \alpha’ F^{\ast}b_{st}\rangle $

Objective Function을 생각하면

$V(f_\alpha^{\ast}+\delta) - (V(f_\alpha^{\ast}) + \langle \nabla V(f_\alpha^{\ast}), \delta\rangle ) = V(f_\alpha^{\ast}+\delta) - (V(f_\alpha^{\ast}) + \langle x_{\alpha}^{*}, \alpha’ F^{\ast}b_{st}\rangle )$

를 생각하면 이를 minimize하는 $\delta$ 는 $V(f_\alpha^{\ast}+\delta)$ 를 minimize하는 것과 동치이다. 따라서, Divergence Update Problem과 Update Problem의 optimal solution $\delta^{\ast}$는 동일하다. $_\blacksquare$

따라서, $f_\alpha^{\ast}$가 있을 떄, $\alpha’$ 에 대한 Divergence Update Problem을 풀어 나온 optimal solution $\delta_{\alpha’}^{\ast}$ 를 합치면 $f_\alpha^{\ast} + \delta_{\alpha’}^{\ast}$ 는 Barrier Problem의 $\alpha + \alpha’$ 에서의 optimal solution.

Restate the Divergence Update problem

minimize하고자 하는 function $V(f+\delta) - (V(f) + \langle \nabla V(f), \delta\rangle )$ 을 $D_V(\delta)$ 라 하자.

$\nabla V(f) = \sum_e \frac{1}{c(e)-f(e)} - \frac{1}{c(e)+f(e)}$ 를 이용하면

\[\begin{aligned} D_V(\delta) &= V(f+\delta) - (V(f) + \langle \nabla V(f), \delta\rangle ) \\ &= \sum_{e} (-\log(c(e) - (f(e) + \delta(e))) -\log(c(e) - (f(e)+\delta(e)))) \\ &- \sum_{e} (-\log(c(e) - f(e)) -\log(c(e) - f(e)))\\ &-\sum_{e}(\frac{\delta(e)}{c(e)-f(e)} - \frac{\delta(e)}{c(e)+f(e)}) \\ &= \sum_{e} - \log(\frac{c(e) - (\delta(e) + f(e))}{c(e)-f(e)})-\frac{\delta(e)}{c(e)-f(e)} \\ &- \log(\frac{c(e) + (\delta(e) + f(e))}{c(e)+f(e)})+\frac{\delta(e)}{c(e)+f(e)} \end{aligned}\]

Notation. $c_+(e) = c(e) - f(e)$ $c_-(e) = c(e)+f(e)$ $D(x) = -\log(1-x)-x$

로 두면 이는

\[\begin{aligned} D_V(\delta) &= \sum_e D(\frac{\delta(e)}{c(e)-f(e)}) + D(-\frac{\delta(e)}{c(e)+f(e)}) \\ &= \sum_e D(\frac{\delta(e)}{c_+(e)}) + D(-\frac{\delta(e)}{c_-(e)}) \end{aligned}\]

가 된다. 이를 알고 Divergence Update problem를 다음과 같이 다시 써보자.

\[\min_{\delta \in \mathbb{R}^m} D_V(\delta)\] \[\text{s.t. } B\delta = \alpha' F^{\ast}b_{st}\]

만약 $D_V(\delta)$ 가 $K$-stable Hessian condition을 만족한다면 Divergence Update problem은 $\tilde{O}(m)$에 Approximation solution을 구할 수 있음을 앞에서 확인한 바 있다.

아쉽게도, $D_V(\delta)$ 는 이를 만족하지 않는다. $D_V(\delta)$는 모든 edge에 대한 함수 $D$의 합인데, 함수 $D$는 1로 갈수록 너무 빠르게 증가하기 때문에 Hessian이 $K$-stable하지 않다.

idea: 함수 $D$를 Taylor 2차 근사를 통해 smoothing하여 Hessian이 상수 범위에 들어가도록 한다!

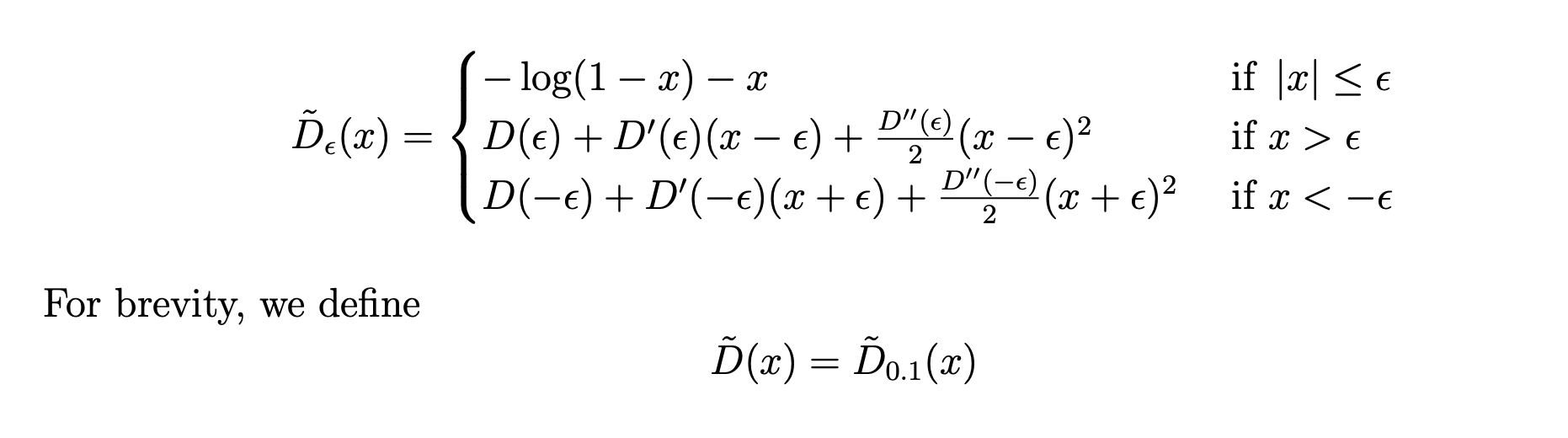
위와 같이 정의한 $\tilde{D}(x)$를 생각하자. 이는 $[-0.1, 0.1]$ 범위에서 완벽히 일치하고, $0.1$보다 클 때는 $0.1$에서, $-0.1$보다 작을 때는 $-0.1$에서 테일러 근사한 함수이다.

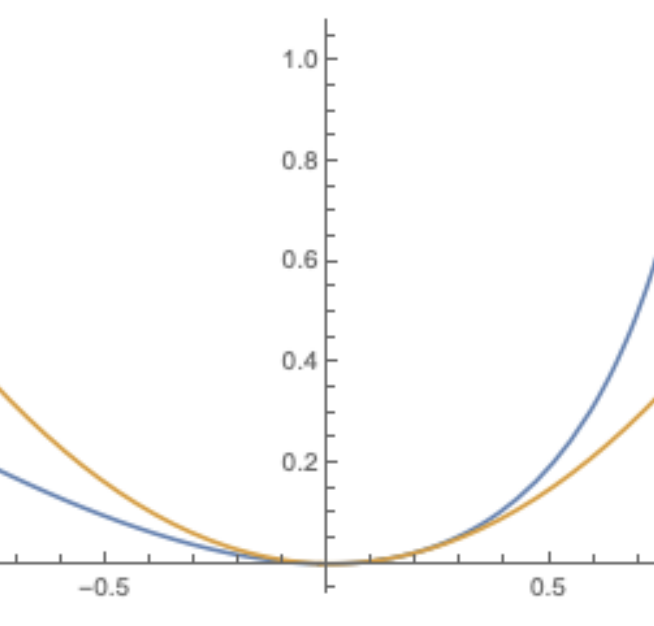
0 근처에서의 $\tilde{D}(x)$와 $D(x)$는 위와 같이 나타난다.

앞서 말했듯이Hessian을 bound하기 위해 $\tilde{D}(x)$를 만들었는데, 실제로 확인해 보면

1. $\frac{1}{2} \le \tilde{D}^{\prime\prime}(x) \le 2$
2. For $x \ge 0$, we have $\frac{x}{2} \le \tilde{D}’(x) \le 2x$ and $-2x \le \tilde{D}’(-x) \le -\frac{x}{2}$
3. $\frac{x^2}{4} \le \tilde{D}(x) \le x^2$

위 식들이 성립한다. 이를 이용해 원래의 Divergence Update Problem을 변형해보자.

Divergence Update Problem의 식에서 $D$만 $\tilde{D}$로 바꾸어

\[\tilde{D}_V(\delta) = \sum_e \tilde{D}(\frac{\delta(e)}{c_+(e)}) + \tilde{D}(-\frac{\delta(e)}{c_-(e)})\]

로 $\tilde{D}_V$를 정의하여

\[\min_{\delta \in \mathbb{R}^m} \tilde{D}_V(\delta)\] \[\text{s.t. } B\delta = \alpha' F^{\ast}b_{st}\]

위 Optimization problem을 Smoothed Update Problem이라 하자. $\tilde{D}_V(\delta)$ 는 strictly convex하며 또한 Lemma 17.1.6에 의해 Hessian이 bound된다. 따라서, 이는 16장에서 확인한

Linear constraint만 존재하는 convex optimization program이 다음 조건을 만족할 때,

• $K$-stable Hessian condition을 만족
• $\mathcal{E}(f)$가 $\sum_e \mathcal{E}_i(f(e))$ 꼴

log 번의 Laplacian equation solving으로 Approx solution을 구할 수 있다. 따라서, $\tilde{O}(m)$시간에 approximation solution을 구할 수 있다.

라는 내용에 완벽히 부합하는 문제이다. 따라서, Smoothed Update problem은 $\tilde{O}(m)$시간에 approximation solution을 구할 수 있다.

Local Agreement Implies Same Optimum

한편, $[-0.1, 0.1]$ 에서 $D$와 $\tilde{D}$ 는 완벽히 agree한다는 성질을 이용하면

$\delta_{\alpha’}^{\ast}$의 크기가 충분히 작을 때 Smoothed Update problem과 Divergence Update Problem의 optimal solution은 일치함을 증명할 수 있고, 이 때 $\alpha’$의 조건으로는 $\alpha’ < \frac{1-\alpha}{20\sqrt{m}}$ 이면 충분하다.

Algorithm

아래 알고리즘을 생각하자.

(단, 위 알고리즘에서 17.6은 Divergence Update Problem이다)

위 알고리즘의 while문은 $O(m^{0.5})$ 번 실행된다. ($1-\alpha$ 가 계속 $1-\frac{1}{20\sqrt{m}}$ factor로 감소)

앞서 $\alpha’ < \frac{1-\alpha}{20\sqrt{m}}$ 에 대해 Divergence Update Problem을 $\tilde{O}(m)$에 풀 수있음을 확인했고, 이에 따라 $\tilde{O}(m^{1.5})$에 undirected maximum flow의 solution을 구할 수 있다. $_\blacksquare$