Gradient Boosting Overview

소개

Machine Learning에 대한 대중적인 인식은 대부분 Deep Learning, Neural Networks에 치중되어 있지만, 그 밖에도 활발하게 연구되면서 활용되고 있는 알고리즘들이 많이 있습니다. 이 글에서는 그 중에서 Gradient Boosting에 알고리즘에 대한 소개와 이해를 목표로 합니다.

신경망의 근간이 되는 Gradient Descent 알고리즘과 이름이 비슷하지만, Gradient Boosting 알고리즘과 Gradient Descent 알고리즘은 구조적으로 큰 유사성이 없습니다. 둘 다 loss function을 최소화한다는 유사점은 있지만, 작동 원리는 상이하며 각자에 기대하는 역할이 구분됩니다.

Gradient Boost 알고리즘은 결정 트리, 랜덤 포레스트 알고리즘에 기반하며, 정형화된 tabular 데이터셋에 대해서 특히 효과적으로 활용됩니다. 신경망은 서로 다른 데이터 필드들이 결국 동일 차원에서 계산되어 normalization을 고려해야 하지만, Gradient Boost에서는 서로 다른 필드들의 값들은 독립적으로 처리되기 때문에 편의상의 이점을 가집니다.

실제로 Gradient Boost류의 알고리즘들은 tabular dataset에서 regression과 classification을 하고 싶은 경우에 바로 out-of-the-box로 활용됩니다. 뿐만 아니라, 알고리즘이 단순하기 때문에 신경망 등의 다른 방법에 비해서 훨씬 더 적은 계산량을 필요로 합니다. 많은 기업들에서 사용되는 DMLC의 XGBoost, MS의 LightGBM 등의 라이브러리를 통해 개선된 Gradient Boost 알고리즘을 활용할 수 있으며, 이를 통해 서비스 DB에서부터 적은 데이터 처리 과정을 거쳐 쉽고 효과적으로 문제를 합리적인 선에서 해결할 수 있습니다.

요약하면, Gradient Boost 알고리즘은

랜덤 포레스트에 기반한 regression 및 classification을 해결하는 ensemble 알고리즘이다.
정형화된 tabular dataset에서 효과적으로 작용하며, 비교적 계산량이 적어 효율적이다.
고도화된 Gradient Boost 알고리즘을 out-of-the-box 로 사용할 수 있는 XGBoost, LightGBM 등의 라이브러리들이 공개되어 있다.

이제 Gradient Boost 알고리즘이 어떻게 동작하는지를 알아봅시다. 예시를 가지고 알고리즘을 단계별로 실행하면 이해하기가 쉬우니, towardsdatascience.com의 예시 데이터를 따라가봅시다.

Regression

Regression (회귀) 문제는 하나의 numerical한 출력값을 입력값들로부터 예측하는 문제입니다. 여기서는 입력값이 X 하나이고, 예측하고자 하는 출력값은 Y라고 둡시다.

학습하고자 하는 데이터셋은 아래와 같다고 합시다.

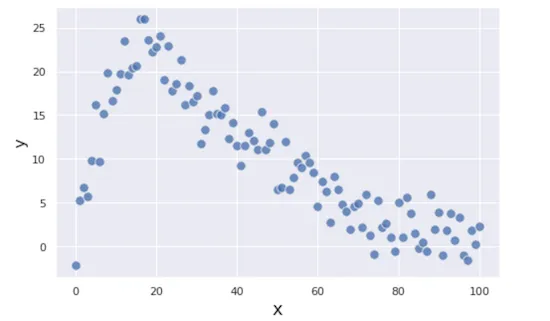
Gradient Boosting은 대략 아래와 같은 단계로 이루어집니다.

초기에는 y를 평균값으로 예측한다.
예측값과 실제값의 편차 (residual)을 구한다.
현재의 residual을 예측하는 작은 결정 트리를 만든다.
만든 결정 트리를 랜덤 포레스트에 추가한다.
랜덤 포레스트로부터 각 데이터의 예측값을 구한다.
필요할 때까지 2-5를 반복한다.

초기 설정

어자피 이후의 개선 작업을 여러 번 반복할 것이기 때문에, 처음에는 아무 적당한 값을 넣어도 상관없습니다. 지금은 y를 예측하고자 하니, 전체 데이터셋에서 y의 평균값을 예측치로 정합시다.

$F_0(x) = avg(Y)$

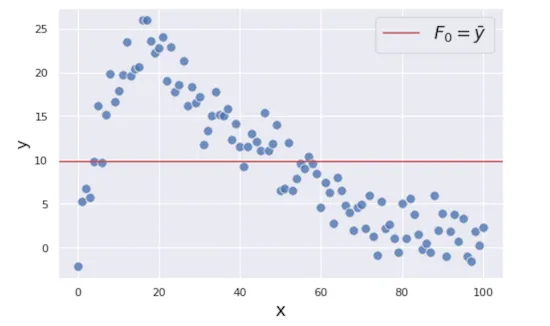
residual 구하기

첫 예측 함수인 $F_0$으로부터 각 데이터에 대한 예측치를 얻을 수 있습니다. 예측치와 실제값의 차이(signed)를 residual로 보고, 각 데이터의 residual을 계산합니다.

이 residual들의 크기를 최소화하는 $F_i$를 만드는 것이 궁극적인 목표입니다. 알고리즘을 멈추는 조건, 어떤 loss function을 가지고 residual을 정의할 것인지는 세부 알고리즘마다 다르지만, 여기서는 가장 간단한 경우를 상정하겠습니다. Loss function은 단순히 $L(y, \gamma ) = (y - \gamma)^2 / 2$ 이고, 반복시행 횟수는 $M=100$회인 것으로 생각합시다.

$m$번째 시행에서의 residual인 $r_m$은 그 이전 단계의 estimator인 $F_{m-1}(x)$에 대해서 일반적으로 아래와 같이 정의될 것입니다.

\[L(y, \gamma) = (y-\gamma)^2/2,\ r_m(x) = y - F_{m-1}(x),\\]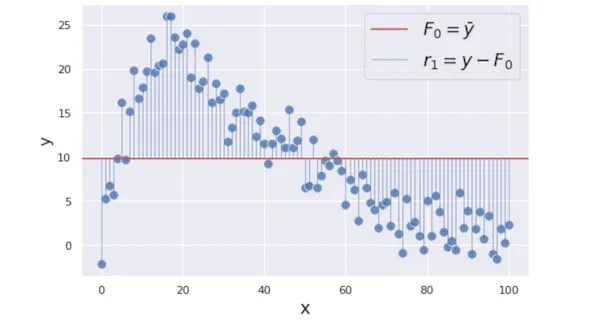

다음 tree 만들기

계산한 residual을 예측하는 결정 트리를 만듭니다. 결정 트리를 만드는 과정에 대해서 고민해야 하는 부분이 세 가지 있습니다.

각 노드가 어떤 입력값 (필드) 을 보도록 할지
각 노드의 판단 threshold를 어떻게 정할지
결정 트리의 크기를 어떻게 제한할지

지금의 예시에서는 입력값이 x 하나이기 때문에 고민하지 않아도 되지만, 일반적인 경우에는 한 데이터가 여러개의 입력값을 가지고 있게 됩니다. 노드의 입력값이 정해졌으면, 데이터를 고르게 가르는 판단 기준치를 정해야 합니다.

이 두 부분은 각 노드에서 greedy하게 결정합니다. 즉, 가능한 모든 입력값을 대상으로 데이터를 나눠보고, 그중에서 가장 loss가 작은 것으로 결정합니다. 입력값이 정해졌을 때 loss를 가장 작게 하는 기준치를 찾는 것은 어렵지 않으니, 각 노드의 조건을 결정하는 것은 효율적으로 계산할 수 있습니다. 이러한 고민들은 일반적인 decision tree regression에서의 고민과 일치합니다. Gradient Boost에서는 원래 설계에 맞게 단순화된 버전으로 넘어간다고 볼 수 있습니다.

결정 트리의 크기가 데이터셋만큼 커지는 것은 계산량 측면에서 비현실적이고, 또 결정 트리가 너무 커지면 overfitting되기가 쉽기 때문에 트리의 크기를 작게 유지해야 합니다. 고도화된 알고리즘마다 트리의 크기를 제한하는 기준이 다르지만, 가장 기본형의 Gradient Boost에서는 8-32개의 리프 노드를 가지도록 제한합니다.

Gradient Boosting을 고도화한 LightGBM, XGBoost 등의 알고리즘들의 결정적인 차이점은 보통 결정 트리를 만드는 과정입니다. 결정 트리를 만들 때 어떤 입력값을 사용하도록 할 것인지, 크기와 모양의 제한은 어떻게 둘것인지 등의 차이로 인해 성능상의 차이가 발생합니다.

위의 방법을 따라서 결정 트리 $h_m(x)$를 만든 것을 아래와 같이 표현할 수 있습니다. 위의 조건을 생략하고 표현했기 때문에 실제 $\arg \min$ 이 아닐 수 있다는 점에 유의합시다.

\[h_m = {\arg \min}_{h_m} L(r_m(x), h_m(x)),\ \gamma _m = h_m(x)\]

아래 오른쪽 그래프에서, 초록색 점들은 원래의 y값들이 아니라, 위 단계에서 계산한 residual이라는 점에 유의합시다.

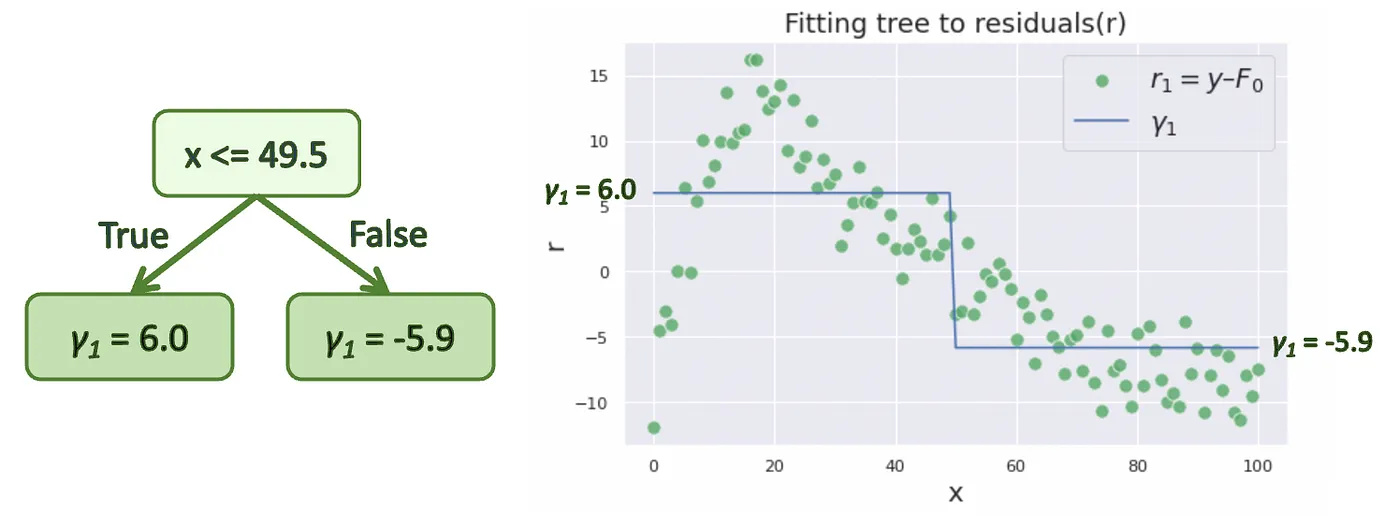
Estimator 업데이트

위에서 만든 결정 트리 $h_m$은 기존의 랜덤 포레스트가 현재까지 놓친 residual들을 잡아주는 역할을 할 것입니다. 그렇기 때문에 $h_m$을 랜덤 포레스트에 더해주면 residual들의 전체적으로 줄어들 것이라고 기대할 수 있습니다.

하지만 방금 만든 결정 트리는 매우매우 단순하고 가볍게 만든 estimator이기 때문에, 온전히 그 값을 더해주면 너무 큰 변동이 있을 수도 있습니다. 또한, 트레이닝 셋의 특징들을 하나하나씩 잡아주면서 학습이 진행되면 overfitting의 가능성이 커질 것이라 생각할 수 있습니다.

그렇기 때문에 learning rate $\nu$ 를 정해서 결정 트리의 주장 $\gamma_m$의 가중치를 줄여줍니다. $\nu$ 는 보통 학습이 진행됨에 따라서 변하지 않으며, 실전에서는 보통 0.1정도의 값을 사용합니다. 지금의 예시 학습에서는 더 큰 $\nu$ 값을 사용했습니다.

\[F_m (x) = F_{m-1} (x) + \nu \cdot \gamma_m\]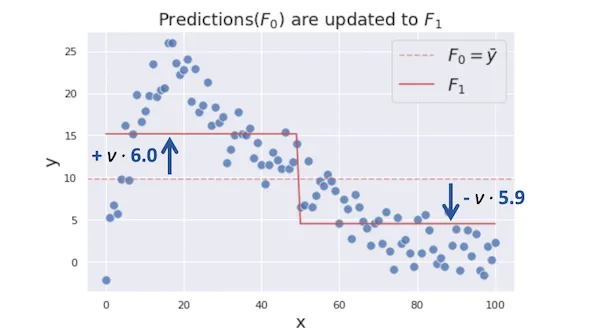

반복하기

이제 더 나은 Estimator를 가지게 되었으니, 다시 2번부터 반복하면 됩니다. 지금의 Residual을 구하고, 그 residual를 최소화하는 가벼운 결정 트리를 만들고, 그 결정 트리를 랜덤 포레스트에 추가하는 과정을 거쳐서 residual을 계속해서 보정해주면 됩니다.

예시 데이터에 대한 반복 결과를 나타내면 아래와 같습니다. Residual이 점점 작아지고, estimator 곡선은 점점 실제 데이터를 잘 표현하게 되는 것을 볼 수 있습니다.

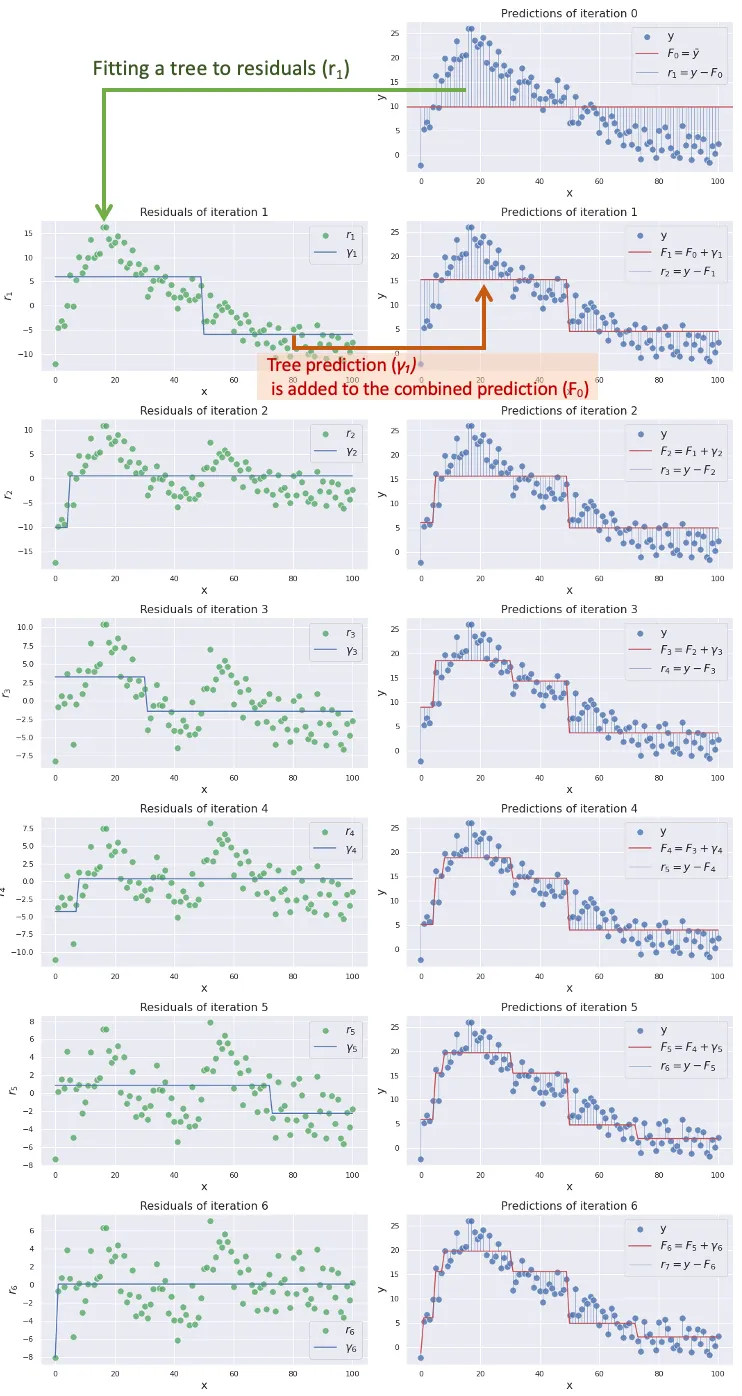
이렇게 $M = 100$회를 반복하면 합리적인 수준의 regressor $F(x)$ 를 얻을 수 있게 됩니다.

Classification

Classification은 해당 데이터의 class가 무엇인지를 분류하는 문제입니다. 일반적으로는 여러 개의 클래스에 대한 문제를 풀어야 하지만, 여기서는 편의상 클래스가 2개인 경우를 상정해 각 데이터에 대해서 yes/no를 예측하는 문제를 생각해보겠습니다. 클래스가 많아지면 모델을 여러 개 두어 각 클래스마다 yes/no를 맞추도록 할 수도 있고, 클래스를 숫자로 embedding하여 threshold를 여러 개 관리할 수도 있고, 몇몇 클래스끼리 묶어서 두 접근 방식을 다 활용할 수도 있습니다.

Classification과 Regression에서의 차이는

학습하고자 하는 값이 다르다.
Loss function이 다르다. 가 있습니다.

여기서는 입력값이 두개인 데이터를 예시로 두어 따라가봅시다. 아래 그림처럼 대략 원형 경계를 가지고 있고, 클래스가 두개인 데이터셋을 학습해봅시다.

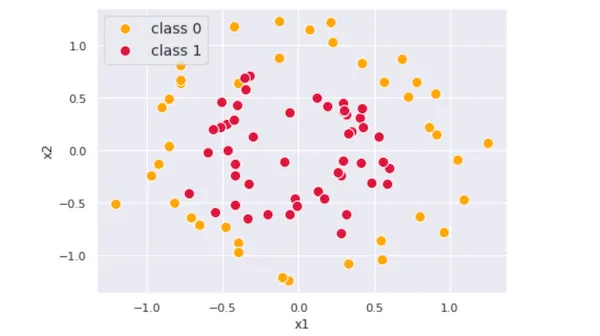
학습 대상

Regression에서는 학습하고자 하는 결과값이 수 하나로 결정되어 있어 그다지 고민할 것이 없었습니다. 하지만 Classification에서는 데이터마다 클래스만 정의되어 있고, 수치값은 없습니다.

지금은 클래스 2개인 경우를 생각하고 있기 때문에, 단순하게 0 / 1로 목표값을 생각해볼 수 있습니다. 바깥쪽 클래스 0을 0, 안쪽 클래스 1을 1로 두고 진행해봅시다.

우리가 학습할 목표값과 우리의 예측치에 대해서 생각해보면, 지금 설정한 값을 ‘클래스 1일 확률 p’ 로 생각해볼 수 있습니다. 확률로 프레이밍을 하게 되면 다양한 제약 조건과 연관 관계들을 생각할 수 있습니다. 기본적으로 0~1 사이의 값을 가져야 하기 때문에 변량의 절댓값에 신경을 많이 써야 하며, 예측치와 실제값 사이의 차이를 두 확률 분포간의 차이로 생각할 수도 있습니다.

우선, 절댓값에 대해서 좀 더 편해지기 위해서, 실제로 학습하는 대상을 확률 $p$ 가 아니라, $s = \log (odds) = \log (p / (1-p))$ 로 생각해봅시다. log-odds로의 변환은 로지스틱 회귀 등등에서 자주 나오는 변환으로, 0~1 사이의 확률값을 $[-\infty, \infty]$ 로 변환해줍니다. 다만, 여기서는 실제로 p=0, 1인 경우들을 계산해줘야 할 수 있으니, 실전에서는 lipping이나 작은 오차항을 넣어줘야 할 수 있습니다.

\[s = \log(odds) = \log( { p \over 1-p } ),\ p = { { e^s } \over { 1 + e^s } }\]

Loss function

앞서 설명한 대로, 우리의 estimator와 실제 목표치가 ‘x를 넣으면 1일 확률이 p인’ 확률 분포 n개들의 모임으로 생각할 수 있습니다.

그렇기 때문에, 두 분포 사이의 차이를 계산하는데 주로 쓰이는 cross-entropy를 사용해서 loss function을 정의하는게 자연스럽습니다. MSE등의 에러를 사용하게 되면 확률값이 가지는 여러 성질들과 맞물리지 않을 수 있기 때문에, classification에서는 주로 cross-entropy loss를 자주 사용하는 것을 볼 수 있습니다. 아래 식에서, y는 0 또는 1이라는 점에 유의합시다.

\[L(y, \gamma) = \sum -p_y \log(p_\gamma) = -y\log \gamma - (1-y) \log (1-\gamma)\]

앞서 regression에서 사용했던 MSE loss ($(y-\gamma)^2/2$)와 다르기 때문에, residual의 계산법 또한 달라지게 됩니다.

Residual을 계산하고자 했던 이유를 다시 생각해보면, 결과적으로 residual을 잘 예측해서 전체 Loss를 줄이기 위함이었습니다. Regression에서는 loss가 MSE였기 때문에, MSE를 가장 잘 줄이는 방향을 판단하기 위해서 residual을 $y - \gamma$로 잡았던 것입니다. 일반화하면, residual r은 loss function L에 대해 다음과 같이 정의할 수 있습니다. $r = - { {\partial L(y, F(x))} \over {\partial F(x)} }$ 즉, 우리는 이때까지 ‘이 loss function을 가장 잘 줄이는 결정 트리를 찾아라!’ 라는 문제를 풀고 있던 것으로 생각할 수 있습니다. 여기서 gradient boosting이라는 이름이 연결되는 것을 알 수 있습니다.

위에서 정의한 loss function을 대입하여 계산해 정리해보면, 아래와 같습니다. $F(x)$가 확률 p가 아닌 log-odds인 s를 따른다는 것에 유의합시다.

\[L(y,s) = - y \log s + \log ( { 1 + e^s })\] \[r = - { { \partial L(y, s) } \over {\partial s} } = y - p\]

기가 막히게도, residual은 여전히 예측치와 목표치의 확률 차이라는 것을 알 수 있습니다. 직관적으로 표현하면, 확률 분포로 이해하여 cross entropy를 최소화하는 방향으로 움직이기 위해서, 확률의 차이가 가장 작아지는 쪽으로 움직이면 된다는 뜻입니다.

새로 만든 트리 적용하기

regression에서는 결정 트리의 리프 노드에 담겨 있는 residual 보정치를 기존의 모델에 적용할때, 단순히 합하면 문제가 없었습니다. MSE를 최소화하는 방향으로 가기 위해서는 예측한 residual를 기존 모델에 더해주는 것으로 충분했기 때문입니다.

하지만, 지금의 경우에는 문제가 있을 것입니다. 확률을 예측하고 있는 기존 모델에, (residual이 그 확률 차이라고는 하나) 예측한 residual을 곧이곧대로 더해주면 우리가 원했던 만큼의 업데이트가 되지 않을 것이기 때문입니다.

정확히 표현하자면, 우리가 만든 결정 트리의 보정값 $\gamma$는 아래와 같은 식으로 계산되어야 합니다.

\[\gamma = {\arg \min} _ \gamma \sum _ {x} L(y, F_{m-1} (x) + \gamma )\]

여기서 합의 대상에 들어가는 $x$는 각 리프노드에 속하는 데이터들입니다. 즉, $y, F_{m-1}(x)$가 주어졌으니, 각 노드별로 loss를 실제로 최소화하는 $\gamma$를 찾아서 기존 결과에 보정해줘야 한다는 뜻입니다. 이는 cross entropy loss에서는 단순히 residual의 평균과 같지 않을 수 있습니다.

실제로 계산해보면, 아래와 같이 나옵니다. (loss function에 대한 2차 근사를 거친 결과입니다.) $\gamma = { {\sum_x (y - p)} \over {\sum_x p(1-p)} }$

이후 과정은 regression과 마찬가지입니다. 이렇게 구한 결정 트리의 보정값 $\gamma$를 estimator에 더해주고, 다시 residual을 구하고, 그 residual을 잘 예측하는 결정 트리를 만들고… 를 반복하면 됩니다.

시각화

위의 데이터를 위와 같은 방법으로 계속해서 반복 학습하면 아래와 같은 과정을 거칩니다.

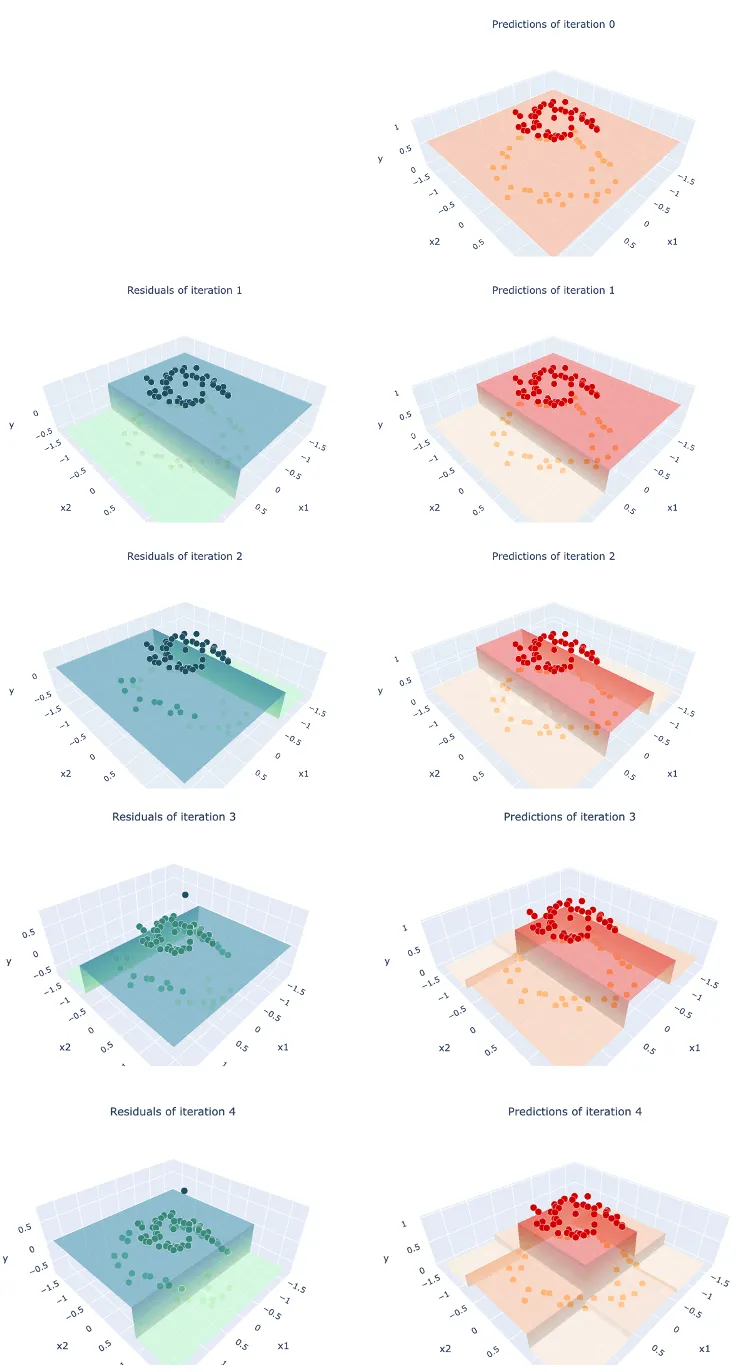
확률값이 클래스 1의 영역에만 제대로 높게 에측되는 것을 볼 수 있습니다.

References

Jerry Friedman의 논문
- https://jerryfriedman.su.domains/ftp/stobst.pdf
towards data science의 설명글
- https://towardsdatascience.com/all-you-need-to-know-about-gradient-boosting-algorithm-part-1-regression-2520a34a502
- https://towardsdatascience.com/all-you-need-to-know-about-gradient-boosting-algorithm-part-2-classification-d3ed8f56541e
StatsQuest의 유투브 설명
- https://www.youtube.com/watch?v=3CC4N4z3GJc
- https://www.youtube.com/watch?v=OtD8wVaFm6E