cs71107's profile image

cs71107

December 25, 2023 19:00

Introduction

동형암호 (Homomorphic Encryption)은 암호문간의 연산을 평문의 정보유출 없이 가능하게 하는 암호 scheme입니다. 간단하게 말해서, 어떤 두 plaintext $m_0, m_1$을 encrypt한 것이 $ct_0, ct_1$이라고 할 때, $dec(ct_0+ct_1) = m_0 + m_1$이 성립합니다. 동형암호 scheme 중에서도, 두 가지 연산, 즉 addition과 multiplication을 제한 없이 사용할 수 있다면 그런 동형암호 scheme을 Fully Homomorphic Encryption, 줄여서 FHE라고 부릅니다. 현재 나와 있는 대부분의 동형암호 scheme의 경우, RLWE problem의 Hardness에 의존하고 있습니다.

대표적인 FHE scheme으로는 BGV, BFV, CKKS, TFHE 등이 있습니다.

동형암호의 경우 그 특성상 Clould computing등의 환경에 적용하는 것이 용이하기 때문에, 이와 관련해서 많은 연구가 이루어지고 있습니다. 그 중에서도 가장 관심을 많이 받는 연구 중 하나는 Matrix Multiplication과 HE를 결합하는 것일 것입니다.

HE가 적용된 상태로 Matrix Multiplication을 할 수 있다는 것은, 안전성과 HE의 장점을 가진 상태로 Matrix Multiplication이 활용되는 다양한 Application을 사용할 수 있다는 것과 같기 때문입니다. 가장 대표적인 Application으로는 역시 Machine Learning이 있습니다. Machine Learning이 주요한 연산들이 Matrix Multiplication으로 표현할 수 있다는 것은 널리 알려진 사실입니다.

이 글에서는 HE를 Matrix Multiplication에 적용하여, Secure하게 Matrix Multiplication을 수행할 수 있는 방법에 대해 설명합니다.

Backgrounds

Operations of CKKS

CKKS scheme의 경우, BFV와 Polynomial Ring $R_q$에 속한 다항식의 쌍으로 Ciphertext가 표현됩니다.

두 Ciphertext $ct_a, ct_b$에 대해, $ct_a = (ct_{a,0}, ct_{a,1}), ct_b = (ct_{b,0}, ct_{b,1})$이면, $ct_a + ct_b = (ct_{a,0}+ct_{b,0}, ct_{a,1}+ct_{b,1})$이 됩니다.

Multiplication의 경우 조금 더 복잡한데, BFV 처럼 3개의 항으로 늘어나고 Relinearization을 통해서 다시 줄어드는 것은 같으나, 세부적인 과정에서 차이가 있고, Rescale이란 과정을 거치게 됩니다.

Encryptoin, Decryption의 경우 BFV와 별로 차이가 없습니다. 예를 들어 Decryption의 경우 secret key를 $s$라 할 때, $ct = (ct_0, ct_1)$에 대해 $m = ct_0+ct_1 \cdot s$입니다.

그 외에 더 자세한 설명은 제안된 논문이나 구글링을 하시면 좋은 자료가 많습니다. BFV의 경우 블로그에 제가 쓴 글들이 있습니다.

Level HE

일부 FHE scheme들의 경우, Ciphertext에 level이 존재합니다. 대표적인 scheme으로는 CKKS의 경우가 있습니다.

CKKS의 경우를 바탕으로 예를 들면, Multiplication을 할 때 마다 level이 하나씩 줄어들게 됩니다.

CKKS에서 Ciphertext는 다항식의 쌍으로 표현됩니다. 그리고 그 다항식의 계수 크기는 parameter에 따라 정해지는데, 일반적으로 매우 큰 수를 선택합니다. BigInteger 같은 것을 쓰면 performance가 떨어질 수 밖에 없기 때문에, 일반적으로는 상한은 적당히 큰 소수들의 곱으로, 계수는 그 소수들에 대한 나머지 쌍으로 equivalent하게 표현할 수 있도록 설정합니다. 이를 Residue Number System, RNS라고 합니다.

이 RNS system을 구성하는 소수들의 개수를 level이라고 합니다. CKKS scheme 에서 Multiplication을 수행할 때, rescale이란 과정을 거치게 됩니다. rescale은 context에 따라 결정된 수 scaling factor를 나눠주는 것과 대응됩니다. scaling factor를 나눠줄 때, RNS system을 구성하는 소수 하나가 빠지게 됩니다. 따라서, Multiplication연산을 1번 수행할 때마다 rescale연산도 같이 수행됩니다. 따라서, Multiplication이 1회 실행될 때마다, level이 1씩 줄어들게 됩니다. 일반적으로 쓰는 parameter의 경우 level의 크기가 아주 크지 않기 때문에, fresh ciphertext의 경우 다른 조작을 하지 않는다고 할 때 수행 가능한 Circuit의 최대 depth가 굉장히 한정됩니다.

이렇다면 FHE란 이름이 붙을 수 없을 것입니다. 이를 해결하기 위한 연산이 바로 Bootrstrapping 입니다.

Bootstrapping

일반적으로 HE scheme들이 가지는 공통점이 있다면, 바로 연산을 반복하면 반복할 수록 error가 늘어난다는 점입니다. addition을 예로 들어봅시다.

secret key가 $s$이고, 두 Ciphertext $ct_a, ct_b$에 대해, $ct_a = (ct_{a,0}, ct_{a,1}), ct_b = (ct_{b,0}, ct_{b,1})$라고 합시다.

이때, $ct_{a,0} + s \cdot ct_{a,1} = m_{a} + e_{a}, ct_{b,0} + s \cdot ct_{b,1} = m_{b} + e_{b}$라고 합시다.

그럼, $ct_a + ct_b = (ct_{a,0}+ct_{b,0}, ct_{a,1}+ct_{b,1})$이고, 이때,

\[dec(ct_a + ct_b) = m_{a} + m_{b} + e_{a} + e_{b}\]

가 되므로, error 항이 늘어나는 것을 확인할 수 있습니다.

사실 Addition의 경우 error가 늘어나는 것이 크게 문제되지는 않습니다. Multiplication의 경우, Addition에 비해 훨씬 더 큰 폭으로 증가합니다.

이렇게 연산들이 반복될 때마다 error가 늘어나고, 결국에는 제대로 Decryption을 할 수 없을 정도로 커지게 되는데, 이렇게 되면 연산, 특히 Multiplication의 횟수에 제한이 생깁니다. 이래서야 FHE라고 할 수는 없습니다. 따라서, 이를 해결하기 위해 error의 크기를 다시 낮추는 연산이 필요한데, 이를 Bootstrapping이라고 합니다.

Bootstrapping이 등장하면서 FHE가 등장했고, 그 후 FHE 연구가 가속화됩니다.

Naive Approach

우선 $d \times d$ matrix 두 개를 곱하는 상황을 상상해봅시다. 먼저 가장 간단하게 생각할 수 있는 naive한 방법은, 한 matrix의 entry 하나 하나를 전부 encrypt 하는 것입니다.

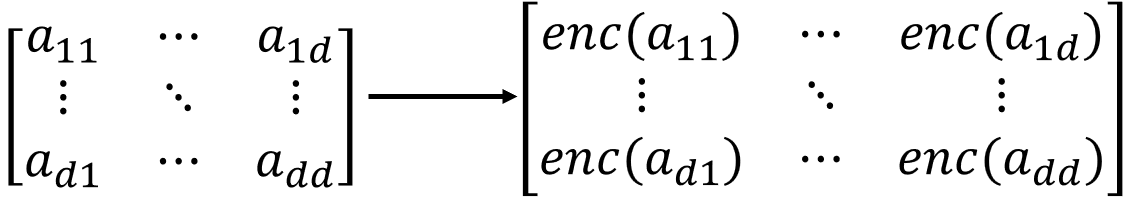
이렇게 하면 총 $d \times d$개의 Ciphertext가 생길 것입니다. 직관적이지만, 굉장히 비효율적 입니다. 그리고 plaintext - Ciphertext 연산이 $O(d^3)$번 시행될 것 입니다. 공간적으로 봐도 $O(d^2)$개의 Ciphertext를 저장할 공간이 필요하니, 시간적, 공간적 복잡도가 모두 매우 크다는 것을 알 수 있습니다.

이를 해결하기 위해서 어떻게 하면 될까요?

Column Order method

위의 방법보다 효율적인 것 중 하나는, 행렬을 Column vector의 모음으로 생각하는 것입니다. 예를 들어서, 어떤 $d \times d$ matrix $A$에 대해,

\[A = \begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,d} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,d} \\ \vdots & \vdots & \ddots & \vdots \\ a_{d,1} & a_{d,2} & \cdots & a_{d,d} \end{bmatrix}\]

라고 두면, 열 벡터 $\textbf{a}_{i}$가 이어져 있는 형태로 생각하면,

\[A = (\textbf{a}_1 \ \vert \ \textbf{a}_2 \ \vert \cdots \vert \ \textbf{a}_d)\]

로 둘 수 있습니다.

이때, 두 $d \times d$ matrix $A, B$에 대해, 위와 같은 식으로 표현한 것을 각각 $A = (\textbf{a}_1 \ \vert \ \textbf{a}_2 \ \vert \cdots \vert \ \textbf{a}_d), B = (\textbf{b}_1 \ \vert \ \textbf{b}_2 \ \vert \cdots \vert \ \textbf{b}_d)$라고 합시다.

$C = AB$라고 두면, $C = (\textbf{c}_1 \ \vert \ \textbf{c}_2 \ \vert \cdots \vert \ \textbf{c}_d)$라고 했을 때,

\[\textbf{c}_i = \sum_{j = 0}^d {b_{j, i}\textbf{a}_j}\]

가 성립합니다.

따라서, $A, B$를 encrypt할 때, 각 entry를 하나하나 encrypt하는 대신, 각 column을 encrypt합시다. (CKKS의 경우 SIMD manner를 통해 가능합니다.) 즉, $ct(A), ct(B)$가 각각 $A, B$를 encrypt한 것이라고 합시다. $ct(A) = (u_1 \ \vert \ u_2 \ \vert \cdots \vert \ u_d), B = (v_1 \ \vert \ v_2 \ \vert \cdots \vert \ v_d)$라고 합시다. $u_i, v_i$는 각각 $\textbf{a}_i, \textbf{b}_i$를 encrypt한 것입니다.

이제, 각 ciphertext $v_i$에서 replicate이란 과정을 통해서 ciphertext $v_{1i}, v_{2i}, \cdots, v_{di}$를 얻읍시다. 이는 column vector의 각 entry를 encrypt한 것에 대응됩니다. 예를 들어서, $v = [2, 3, 5, 7]^T$라고 두면, 순서대로 $[2, 2, 2, 2]^T, [3, 3, 3, 3]^T, [5, 5, 5, 5]^T, [7, 7, 7, 7]^T$을 encrypt 한 것을 구하는 것과 같습니다. replicate의 원리는 다음과 같습니다.

현재 $v_i$는 encrypt된 상태이기 때문에, 각 entry의 값을 알 수 없는 상태입니다. 할 수 있는 연산은 rotate, addition 처럼 제한돼있는 상태입니다. 그렇기 때문에, 위와 같이 rotate를 적절히 활용해 원하는 vector에 대응되는 Ciphertext를 만들어주는 것입니다.

$C$를 $A, B$처럼 encrypt한 것을 $ct(C) = (w_1 \ \vert \ w_2 \ \vert \cdots \vert \ w_d)$라고 할 때,

\[w_i = \sum_{j = 0}^d {v_{j, i}u_j}\]

위 식에서 $v_{j, i}, u_j$의 경우 모두 homomorphic 하게 구할 수 있으므로, 원하는 목적을 달성하게 됩니다.

위 과정을 간단히 그림으로 나타내면 아래 그림과 같습니다.

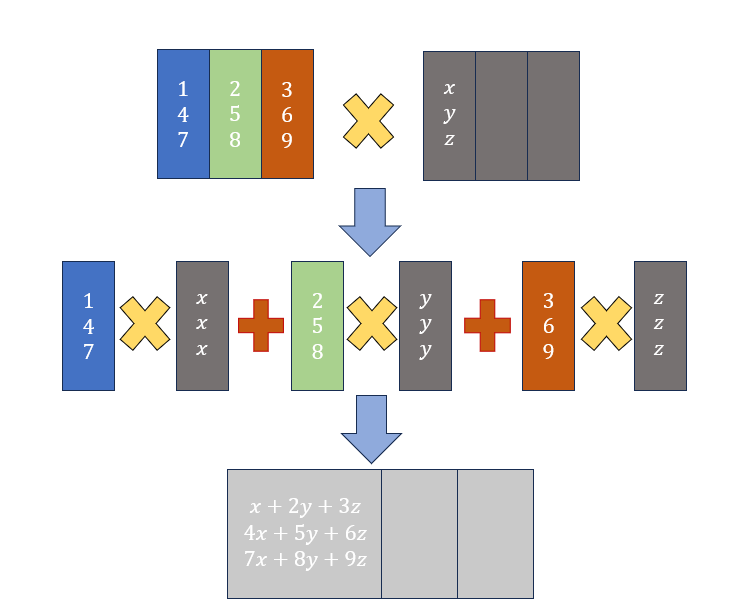
Matrix Multiplication Order

이제 여러 개의 matrix가 있을 때, 그 순서를 어떻게 할지 생각해봅시다.

Sqaure Matrix Order

먼저 $d \times d$ matrix들이 여러 개 있을 때 순서를 어떻게 할지 생각해 봅시다.

모든 matrix의 크기가 같으니, 순서대로 하면 될까요?

plaintext라면 그래도 상관없었을 것입니다. 하지만, 지금은 Ciphertext로 encrypt 된 상태라는 걸 기억해야 합니다. 즉, level이 존재하고, level이 최대한 적게 깎여나가도록 해야 할 필요가 있습니다.

Matrix Multiplication은 교환법칙이 성립하지 않고, 결합법칙만 성립한다는 것, 따라서 중간 결과값의 경우 항상 특정 연속 구간의 matrix들을 곱한 결과가 된다는 것을 생각하면, 연산의 과정은 binary 트리에 대응되고, 깎이는 level의 크기는 binary tree의 depth가 커지면 커질 수록 커집니다. 따라서, 이를 최소화 하기 위해서는 depth를 최대한 작게 해야 하고, 이는 총 $N$개의 matrix를 곱한다고 했을 때, 최대 $\lceil \log(N) \rceil$ 만큼의 depth를 가지게 할 수 있습니다.

10개가 있다고 하면, 다음 그림과 같은 순서로 곱해지게 하면 됩니다.

General Case order

만약에 Sqaure matrix가 아니라 일반적인 크기의 matrix를 곱한다면, 곱셈 횟수를 우선시하게 되는데, 이는 dynamic programming을 통해서 최소 횟수를 구할 수 있음이 널리 알려져 있습니다.

링크에서 직접 풀어볼 수도 있으며, 그 시간복잡도는 matrix의 개수 $N$에 대해 $O(N^3)$ 입니다.

사실 더 좋은 복잡도로 구할 수 있음이 널리 알려져 있는데 관련 알고리즘을 사용하는 문제로는

링크가 있습니다. 자세한 알고리즘은 구글링을 통해서 찾으실 수 있습니다.

Conclusion

Matrix Multiplication은 application이 많은 연산으로서, 이를 secure하게 계산하는 것은 매우 중요합니다. 이 글에서는 HE를 적용하여 secure하게 Matrix Multiplication을 수행하는 방식에 대해 알아보았습니다. 하지만 최근 많은 연구가 진행됐고, 소개한 방식보다 더 나은 복잡도를 가지는 알고리즘들도 존재합니다. 그것은 아직 제가 공부를 못했기 때문에, 다음 글을 쓸 기회가 있으면 소개하도록 하겠습니다.

글 후반부에 소개한 행렬곱셈순서에 대한 문제는 PS를 하시는 분들이라면 쉽게 혼자서도 유도하실 수 있을 것이라 생각합니다. PS가 활용될 수 있는 예중 하나라고 할 수 있을 것 같습니다.

부족한 글 읽어주셔서 감사합니다.

Reference

• Secure Outsourced Computation of Multiple Matrix Multiplication Based on Fully Homomorphic Encryption, Shufang Wang, Hai Huang