January 27, 2024 19:00

Introduction

지금까지는 주로 동형암호(Homomorphic Encryption)의 scheme들에 관해 글을 써왔는데, 이번 글에서는 동형암호와 관련돼 있는 연구 분야 중 하나인 Circuit Privacy에 관련된 Sanitization에 관련된 글을 써보려고 합니다.

이 글에서는 Ducas - Stehlé Washing machine에 대해서 중점적으로 설명하도록 하겠습니다. 원 논문은 이 링크에서 확인하실 수 있습니다.

Backgrounds

Homomorphic Encryption

동형암호 (Homomorphic Encryption)은 암호문간의 연산을 평문의 정보유출 없이 가능하게 하는 암호 scheme입니다. 지금까지 쓴 글들에 설명이 자세하게 나와 있으니, 자세한 설명은 생략하겠습니다.

Bootstrapping

동형암호들의 경우 error를 필수적으로 가지게 되는데, 이 error는 연산을 반복하면 반복할 수록 커진다는 특징이 있습니다. 이 error가 한계를 넘어서면, decrypt를 할 때 correctness를 보장할 수 없게 됩니다. 이를 해결하기 위해서, FHE에서는 bootstrapping이라는 것이 존재하여, error의 크기를 줄여줍니다.

Statiscal Distance

어떤 countable set $S$에 대해, $S$에 대한 probability distribution을 $D$라고 합시다.

$x \in S$에 대해, $D(x) = Pr[\tilde{x} = x \vert \tilde{x} \leftarrow D]$

$S$에 대한 random variable $X, X’$에 대해, $X, X’$가 각각 $D, D’$를 따른다고 합시다. 두 random variable $X, X’$의 statiscal distance는 다음과 같이 정의합니다.

정의에 의해 $0 \le \Delta (X, X’) \le 1$을 항상 만족합니다. 혼동의 여지가 없다면, $\Delta (X, X’) = \Delta(D, D’)$로도 씁니다.

$\Delta (X, X’) = \delta < 1$ 에 대해, intersection distribution $C = D \cap D’$는 다음과 같이 정의됩니다.

$C$가 valid한 정의라는 것은 $2 min(a, b) = a+b - \lvert a-b \rvert$를 이용하면, $\sum _ {x \in S} C(x) = 1$이 되어 valid한 정의임을 알 수 있습니다.

마지막으로, 두 distribution의 mixture를 $0 \le \alpha \le 1$에 대해

위와 같이 정의합니다. $B(x) = \alpha \cdot D(x) + (1-\alpha) \cdot D’(x)$이고, $\sum _ {x \in S} B(x) = 1$ 임을 쉽게 확인할 수 있습니다.

직관적으로, mixture의 경우 확률이 $\alpha$인 Bernoulli distribution에 따라 시행 했을 때 $0$이 나오면 $D$를 따라서, $1$이 나오면 $D’$를 따라서 추출한다고 볼 수 있습니다.

statiscal distance가 security parameter $\lambda$에 대해

이면, 두 확률변수 $X, X’$가 statiscally close하다고 하고, $X \approx _ {s} X’$로 씁니다. statiscally closeness는 computationally indistinguishability를 imply 합니다.

Sanitizability and Circuit Privacy

먼저 동형암호에서 Ciphertext Sanitizability가 무엇인지 알아봅시다.

Ciphertext Sanitizability는 PPT (Probabilistic Polynomial Time) algorithm인 Sanitize가 존재성을 의미합니다. secret key $sk$에 대응되는 public key $pk$, 그리고 ciphertext $ct$에 대하여, $ct$가 plaintext $\mu$를 encrypt한다고 합시다. 이때, Sanitize는 public key $pk$와 ciphertext를 입력으로 받는 함수 입니다. 그리고 $Sanitize(pk, ct)$와 $Sanitize(pk, Enc(\mu, pk))$가 statiscally (computationally) indistinguishable 하다는 성질을 가집니다.

Ciphertext Sanitizability가 어떻게 Circuit Privacy와 관련돼 있는지 살펴봅시다.

먼저 python으로 작성한 다음과 같은 두 함수를 생각해 봅시다.

첫 번째 함수는 다음과 같은 logic을 가집니다.

def f1 (x, a, b):
    temp = x + b
    ans = a * temp # a*(temp) = a*(x+b) = a*x + a*b
    return ans

두 번째 함수는 다음과 같은 logic을 가집니다.

def f2 (x, a, b):
    temp1 = a * x
    temp2 = a * b
    ans = temp1 + temp2 # temp1 + temp2 = a*(x+b) = a*x + a*b
    return ans

컴퓨터 환경등으로 발생하는 effect(overflow 등)를 무시한다고 가정하면, 두 함수는 같은 입력에 대해 같은 결과를 낼 것입니다.

그림으로 첫 번째 로직을 표현하면 다음과 같습니다.

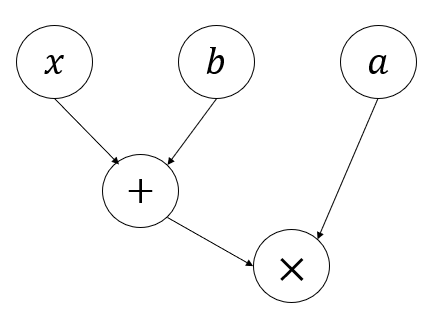
그림으로 두 번째 로직을 표현하면 다음과 같습니다.

그렇다면 다음과 같은 protocol을 하는 상황이 있다고 합시다. Alice는 $x, a, b$를 Bob에게 보내고, Bob은 $1/2$ 확률로 f1의 logic을, $1/2$확률로 f2의 logic을 사용해서 계산하여 그 결과를 다시 Alice에게 보낸다고 합시다.

아래 그림이 현재 상황을 표현하고 있습니다.

컴퓨터 환경등으로 발생하는 effect(overflow 등)를 무시한다면, Alice가 Bob이 f1의 로직을 썼는지, f2의 로직을 썼는지 $1/2$보다 높은 확률로 알 수 있을까요?

아마 없을 겁니다. f1과 f2는 완전히 같은 값을 return하기 때문입니다.

이제, 비슷한 상황을 생각해봅시다. Alice는 $x, a, b$를 가지고 있는 HE의 secret key로 encrypt한 후 보냅니다. 그리고 public key (evlaution key등 포함)를 broadcast합니다. Bob은 $1/2$ 확률로 f1의 logic을, $1/2$확률로 f2의 logic을 사용해서 계산합니다. public key가 있으므로, f1의 logic이든 f2의 logic이든 모두 연산 가능합니다. 그리고 결과로 나온 ciphertext를 다시 Allice에게 보낸다고 합시다. Alice는 받은 ciphertext를 가지고 있는 secret key를 사용하여 decrypt하여 최종 결과를 얻습니다.

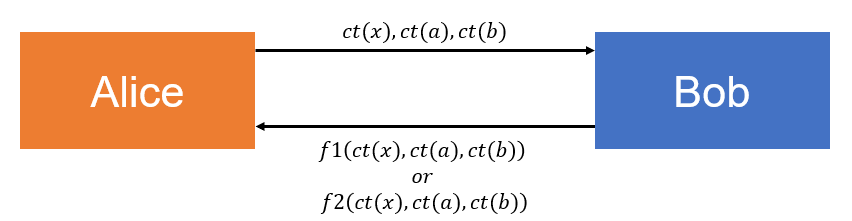
자, 이번에도 Alice가 Bob이 f1의 logic을 썼는지, f2의 logic을 썼는지 구분할 수 없을까요? 이제는 상황이 좀 다릅니다. Alice가 secret key를 알고 있으므로, Alice는 결과 외에도, 반환받은 Ciphertext의 error를 얻을 수 있게 됩니다. 따라서, Circuit의 정보가 error를 통해 leak이 될 수 있습니다. 만약 leak된 정보가 critical하다면, $1/2$보다 더 높은 확률로 사용한 로직을 예측할 수도 있을 것입니다.

만약 Ciphertext Sanitizability가 있다면, Sanitize가 존재한다는 뜻입니다. 따라서, Bob이 Alice한데 결과인 $ct_res$를 바로 보내는 대신, $Sanitize(pk, ct_res)$를 보낸다고 합시다. f1의 logic을 썼을 때의 결과를 $ct_1$, f2의 logic을 썼을 때의 결과를 $ct_2$라고 합시다. 그렇다면 정의에 따라, Alice는 $Sanitize(pk, ct_1)$과 $Sanitize(pk, Enc(\mu_res, pk))$를 구분할 수 없고, $Sanitize(pk, ct_2)$과 $Sanitize(pk, Enc(\mu_res, pk))$도 구분할 수 없습니다. 즉, $Sanitize(pk, ct_1)$과 $Sanitize(pk, ct_2)$를 구분할 수 없습니다. 즉, f1의 logic을 썼는지, f2의 logic을 썼는지 구분할 수 없습니다. 따라서, Circuit Privacy를 얻을 수 있습니다.

Noise Flooding

Noise Flooding은 Washing Machine과는 살짝 다른 방식입니다.

Washing Machine과 Noise Flooding 모두 error의 ‘정보’를 ‘지우는’ 방식입니다.

다만 Noise Flooding의 경우, 여러 번의 과정을 반복하기 보다는 한번에 기존 error 보다 훨씬 더 큰 (분포의) error를 더해서 기존 error의 정보를 지웁니다.

좀 더 구체적으로 설명하겠습니다. 실제로 HE 등의 error distribution의 경우 discrete하게 뽑히지만, 설명의 편의를 위해서 continuous한 분포에서 설명 합니다.

기존 에러가 어림잡아 $e \sim N(0, \sigma^2)$라고 ‘가정’합시다. Noise Flooding의 경우, $e’ \sim N(0, \sigma’^2)$에서 $e + e’$를 반환하게 합니다. 이때, $sigma’ \ge 2^{\lambda} sigma$입니다. 이럴 경우 $e’ \approx _ {s} (e+e’)$가 됩니다. 즉, computationally indistinguishable 합니다. 즉, $e$를 몰라도 simulate할 수 있고, $e$의 정보를 지운다고 생각할 수 있습니다.

Lemma for Proofs

이 절에서는 Statiscal Distance와 관련된 여러 가지 lemma에 대해 설명하도록 하겠습니다.

Lemma 1.

$0 \le \delta < 1$에 대해, $\Delta(B, B’) \le \delta$를 만족하는 distibution $B, B’$가 존재한다면, 다음을 만족하는 distribution $D, D’$가 존재한다.

proof: $C = B \cap B’$라고 하고, $D(x) = (B(x) - (1- \delta) \cdot C(x)) / \delta$로 정의하면 됩니다. $D’$로 비슷하게 정의할 수 있습니다.

Lemma 2.

$0 \le \alpha \le 1$과, 임의의 distribution $C, D, D’$에 대해, 다음이 성립한다.

proof: $2 \Delta ((1- \alpha) \cdot C + \alpha \cdot D, (1- \alpha) \cdot C + \alpha \cdot D’) = \sum \lvert ((1- \alpha) \cdot C(x) + \alpha \cdot D(x)) - ((1- \alpha) \cdot C(x) + \alpha \cdot D’(x)) \rvert = \sum \lvert \alpha \cdot D(x) - \alpha \cdot D’(x) \rvert = \alpha \sum \lvert D(x) - D’(x) \rvert = 2 \alpha \Delta (D, D’)$ 에서 증명이 끝납니다.

Lemma 3.

$0 \le \delta \le 1$와 randomized function $f : S \rightarrow S$가 임의의 $a, b \in S$에 대해 $\Delta (f(a), f(b)) \le \delta$를 만족할 때, 모든 $k \ge 0$에 대해 다음이 성립한다.

임의의 $a, b \in S$에 대해

proof: 수학적 귀납법을 사용합니다. $k = 0$일 때는 정의에 의해 증명이 끝납니다. 이제, $k \le m$인 $k$에 대해 성립한다고 가정합시다. $k = m+1$일 때, Lemma 1. 에 의해서, 다음과 같은 distribution $D, D’$가 존재합니다.

따라서, 양변에 $f$를 compose하면 아래와 같습니다.

Lemma 2.에 의해서, 다음이 성립합니다.

이때, 다음과 같이 계산하면

에서,

따라서, $\Delta (f(D), f(D’)) \le \delta$이므로, 증명이 끝납니다.

Properties and Construction of Sanitize

Properties of Sanitize

Sanitize의 정의 (정확히는, Ciphertext Sanitizability의 정의)는 이미 Backgrounds에서 다루었으므로, 이 절에서는 만족해야 하는 성질에 대해서 알아보겠습니다.

Sanitize의 경우 크게 두 가지 성질을 가집니다.

• Message Preserving
• Ciphertext Sanitizability

첫 번째 성질의 경우, 어떤 ciphertext $ct$가 sanitization을 거치더라도 가지고 있는 message의 정보에 영향이 없다는 것을 의미합니다. 수식으로 표현하면 다음과 같습니다. ciphertext 공간을 $C$라고 할 때,

두 번째 성질의 경우, 다음과 같이 표현할 수 있습니다.

Construction of Sanitize

먼저, 다음의 두 함수 Refresh와, Rerand를 생각해봅시다.

Refresh의 경우, ciphertext의 noise error를 일정 수준 이상으로 낮춰주는 함수입니다. 대부분의 FHE scheme에서 bootstrapping에 해당한다고 볼 수 있습니다.

수식으로 쓰면 다음과 같은 성질을 만족하는 함수입니다. noise error의 크기가 작은 Ciphertext의 공간을 $C^{*}$라고 합시다.

Rerand의 경우, $C^{*}$에 속하는 ciphertext들을 다시 randomize해주는 함수입니다. 수식으로 쓰면 다음과 같습니다.

이제, Refresh와, Rerand를 정의했으니, 두 함수의 합성인 Wash함수를 정의합니다.

Wash는 다음과 같습니다.

즉, Refresh와, Rerand의 합성입니다.

Wash의 경우, 적당한 $\delta < 1$에 대해 다음이 성립합니다.

이제 적당한 $k$에 대해서, Sanitize함수를, Wash함수를 $k$번 compose한 것으로 정의합시다. $Wash_pk$가 주어진 $pk$를 사용하는 Wash함수라고 한다면, Sanitize함수를 다음과 같이 정의할 수 있습니다.

이때, 앞선 Lemma 3에서 $S$를 $C$로, $Wash_pk$를 $f$로 생각하면, Lemma 3에 의해서 다음이 성립합니다.

적당히 큰 $k$에 대해서, $\delta^{k} \le negl(\lambda)$이므로, $k$를 잘 설정해주면, 원하는 Sanitize함수를 construct할 수 있습니다.

Sanitize Building - Regev Ciphertext

이제 실제 scheme들에 위에서 구성한 Sanitization 알고리즘을 어떻게 쓸 수 있는지 살펴봅시다. 다음과 같이 LWE-encryption들의 집합을 정의합시다.

$\textbf{s}$는 secret key를, $q$는 modulus를, $\mu$는 plaintext를, $\eta$는 error rate을 의미합니다. 즉, $\lvert e \rvert < \eta q$ 입니다.

이제 public key가 다음과 같은 $l \ge O(nlogq)$개 이상의 fresh encryption of zero를 포함한다고 합시다. 즉, public key에는 $ 1 \le i \le l$에 대해, 다음과 같이 $r_i$들을 생성합니다.

여기에서 각 $r_i$들은 independently하게 생성됐습니다. 이제, Rerand함수를 다음과 같이 정의합시다.

이때, $f$의 경우 $[-B, B]$에서 uniformly random하게 추출하고, $\varepsilon_{i}$는 Rerand함수를 실행할 때 마다 ${ -1, 0, 1}$ 중에서 uniformly random하게 선택합니다.

이때,

위와 같이 $ct’$를 정의하면, left over hash lemma에 의해서, $\textbf{a}’$의 distribution은 uniform distribution과 indistinguishable합니다. 따라서, 이제 기존 ciphertext의 정보는 $e’$에만 남게 됩니다.

그리고 $\lvert e’ \rvert < (l+1) \cdot \eta \cdot q$가 성립합니다.

그리고 임의의 $x, y$에 대해 $ -(l+1) \eta q < x, y < (l+1) \eta q$이면,

따라서, 임의의 $ct_0, ct_1 \in LWE_{\textbf{s}}^{q}(\mu, \eta)$에 대해,

가 되고, 이제 이것을 적절한 횟수만큼 반복하면 됩니다. 예를 들어, $\delta \approx 2^{-16}$이고, 128-bit security를 달성해야 해서 $negl(\lambda) = 2^{-128}$이라고 하면, $\delta ^ k \le negl(\lambda)$ 여야 하므로, $k \ge 8$이니까, 8회 이상 반복하면 됩니다.

Conclusion and Discussion

지금까지 FHE에서의 Ciphertext Sanitizability를 알아보았습니다. 이 글에서 소개한 것은 Ducas - Stehlé Washing machine 기법으로, FHE에서 공통적으로 적용될 수 있는 기법이면서 유명한 기법입니다.

글의 결과를 요약하면 결국 Wash라는, circuit의 정보를 담고 있는 error의 정보를 순차적으로 지워나갈 수 있게 해주는 함수를 정의한 후, 반복적용한다는 것입니다.

여기서부터는 글을 읽으면서 생길 수 있는 몇 가지 의문점들에 대한 대답입니다.

Q. Bootstrapping을 그냥 쓰면 되는 거 아닌가요?

A. Bootstrapping의 경우 Decryption과 Re-encryption을 혼동해서 나오는 질문 중 하나입니다. Re-encryption의 경우 기존에 있던 error가 Decrypt 과정에서 날아가고, 새로운 fresh error를 추출하지만, Bootstrapping의 경우 Decryption을 Homomorphic하게 하는 것으로, 기존에 있는 Ciphertext의 정보가 완전히 사라진다고 보장할 수 없습니다. 그렇기 때문에 Washing Machine에서 Refresh를 Rerand를 거쳐서 ‘여러 번’ 사용하는 것입니다.

Q. Background에 나오는 Noise Flooding이 훨씬 더 간단해 보이는데, 그냥 적용하면 안 되나요?

A. Noise Flooding의 경우 같이 설명했듯이, 기존의 정보를 덮어서 없애버릴 수 있는 큰 분포에서 더해야 하는 항 (error)를 추출하는데, TFHE와 같은 일부 scheme들의 경우 parameter set이 빡빡한 경우가 많기 때문에, Noise Flooding을 적용할 수 있을 만큼 여유가 있지 않은 경우가 많습니다. 특히나 TFHE의 경우 error를 정말 한계 크기까지 허용하는 느낌이라, 더욱 적용하기 어렵습니다.

Q. Washing Machine에서 한계점이 있을까요?

A. Washing Machine을 구성하는 core 함수 중 Refresh 함수의 경우 대부분 bootstrapping이 사용됩니다. (error 크기를 일정 수준으로 줄여야하므로) 하지만, 대부분의 FHE scheme에서 bootstrapping의 경우 아주 시간이 오래 걸립니다. 그렇기 때문에, 할 수 bootstrapping을 ‘반복’하는 행위 자체가 매우 부담으로 작용하게 됩니다.

지금까지 Ducas - Stehlé Washing machine을 소개했습니다. 부족한 글 읽어주셔서 감사합니다. 이 글에서 소개한 technique의 원 논문은 여기에서 확인할 수 있습니다.

Reference

• https://eprint.iacr.org/2016/164.pdf