Garbled Circuit and Functional Encryption
Introduction
이 글에서는 Multi-party computation(MPC)에서 사용되는 Garbled Circuit과 Oblivious Transfer에 대해 알아볼 것입니다. 그 뒤에는 public key encryption을 확장한 개념인 Functional Encryption이라는 개념을 소개할 것입니다. 배경지식이 크게 필요하지 않도록 작성했기 때문에, 암호학에 관심이 있는 독자들에게 흥미를 줄 수 있기를 바랍니다.
Garbled Circuit
Garbled Circuit(GC) 는 두 사람 $Alice$와 $Bob$이 각각 input $x$와 $y$를 갖고 있을 때, 서로에게 자신의 input을 노출하지 않고 $f(x,y)$를 계산하는 two-party computation을 위해 고안되었습니다. 이는 필자의 직전 포스트인 two-party communication 모델과 동일하지만, 자신의 input에 대한 정보를 드러내서는 안된다는 조건이 추가적으로 붙은 형태입니다.
이제 무려 1986년에 발표된 Yao’s protocol에 대해 AND Gate의 예로 살펴볼 것입니다.
Garbling a AND gate
Garbled Circuit을 이용한 two-party computation에서 두 사람은 각각 Garbler와 Evaluator라는 역할을 맡습니다.
Garbler는 계산해야 하는 circuit이 주어졌을 때, garbled circuit을 만드는 역할을 합니다.
Evaluator는 Garbler로부터 정보를 받아 garbled circuit을 evaluate하여 원래 circuit의 결과를 얻는 역할입니다.

위와 같은 AND gate를 생각해 봅시다.
Garbler는 각 wire $A, B, C$와 그 wire의 값으로 가능한 value인 $0, 1$에 대해 수 하나씩을 생성하여 대응시킨다. 즉, 값 $A_0, A_1, B_0, B_1, C_0, C_1$을 생성합니다. 이를 Garbled Value라 합니다.
그 후, Encryption scheme $Enc$로 다음과 같은 값들을 계산하고, 값들을 random하게 permute해 놓습니다.
$Enc(A_0B_0, C_0)$ $Enc(A_0 \mid\mid B_1, C_0)$ $Enc(A_1 \mid\mid B_0, C_0)$ $Enc(A_1 \mid\mid B_1, C_1)$
이 때 $s \mid\mid t$는 비트스트링 $s$와 $t$의 concatenation입니다. 예를 들어, $s=0,t=1$이면 $s \mid\mid t$는 $01$이 됩니다.
그러면, $A_x$와 $B_y$가 주어졌을 때 $C_{x \land y}$로만 위 4개의 값중 하나를 얻어낼 수 있습니다. 또한, $C_{x \land y}$가 $C_0$인지 $C_1$인지는 알 수 없습니다.
Yao’s Protocol
Yao’s protocol은 two-party computation을 compute하는 protocol이며, garbled circuit을 사용합니다.
AND Gate에 대한 Yao’s Protocol은 다음과 같습니다.
-
Garbler가 가지고 있는 input은 $x \in \{0, 1 \}$, Evaluator가 가지고 있는 input은 $y \in \{0, 1 \}$이라고 합시다.
-
Garbler는 Encryption scheme $Enc$를 준비하고, $A_0, A_1, B_0, B_1, C_0, C_1$을 생성합니다.
- Garbler는 Evaluator에게 다음과 같은 값을 전달합니다.
- $cts = [Enc(A_0 \mid\mid B_0, C_0)$, $Enc(A_0 \mid\mid B_1, C_0)$, $Enc(A_1 \mid\mid B_0, C_0)$, $Enc(A_1 \mid\mid B_1, C_1)]$
- $A_x$
- $shuffle([C_0,C_1])$
- Translation table $T =[(C_0,0), (C_1,1)]$
-
Evaluator는 Garbler에게 $B_y$를 받아옵니다. 단, 이 때 Alice는 $y$에 대한 정보를 얻지 못하며, Bob도 $B_{1-y}$의 정보를 얻지 못합니다. (이를 Oblivious Transfer라고 하며, oblivious transfer를 하는 방법에 대해서는 다음 절에 소개할 것 입니다.)
-
Evaluator는 $shuffle([C_0,C_1])$의 각 원소에 $c$에 대해 $Enc(A_x \mid\mid B_y, c)$를 계산합니다. $Enc(A_x \mid\mid B_y, c) \in cts$가 성립하는 $c$가 $C_{x \land y}$임을 알 수 있습니다.
- Evaluator는 translation table $T$을 보고 $x \land y$을 얻습니다. 이 값을 Garbler에게도 전달합니다.
위 프로토콜에서 최종 evaluation 값을 제외하고 Evaluator가 $x$에 대해 얻는 정보는 $A_x$뿐이며, Oblivious transfer가 가능하다면 Garbler도 $y$에 대해 추가적으로 얻을 수 있는 정보가 없습니다.
이 프로토콜에서는 $cts$의 정보를 이용해 $A_x, B_y$를 input으로 하고 $C_{x \land y}$를 output으로 하는 gate를 계산합니다. 일반적으로, circuit $C$에 대해 $x$와 $y$에 대해 $x$의 garbled value와 $y$의 garbled value를 input으로 하고 $C(x,y)$의 garbled value를 output으로 하는 circuit을 Garbled Circuit이라 합니다.
즉, 위 protocol은 다음과 같은 4가지 부분으로 이루어집니다.
-
Garbled Circuit의 구성 (Garbled Circuit의 계산에 필요한 각 게이트의 $cts$ 정보 전달 등도 여기에 포함됩니다).
-
input의 garbled value 전달
-
Evaluator의 Garbled Circuit의 Evaluation
-
Translation table을 이용한 최종 값 계산
이를 확장하면 일반적인 Boolean Circuit에 대해 Yao’s Protocol을 하는 방법을 얻을 수 있습니다.
-
Setting: Alice (Garbler)가 vector $x = (x_i)$를, Bob(Evaluator)가 vector $y = (y_i)$를 가지고 있을 때 function $F$에 대해 $F(x,y)$를 계산하고자 합니다. $F$의 circuit representation을 $C$라 합시다.
-
Alice는 $C$의 각 wire $W$에 대해 garbled value $W_0, W_1$을 생성하고, 또한 각 gate $g$에 대해 가능한 Encryption의 결과값인 $cts_g$를 계산합니다.
-
Alice는 자신의 input $x_i$들에 대한 garbled value 및 모든 $cts_g$, 그리고 각 wire의 permuted garbled values $shuffle(W_0, W_1)$, 마지막 out에 대한 translation table $T$를 Bob에게 전달합니다.
-
Bob은 Oblivious Transfer를 통해 자신의 $y_i$에 대한 Garbled Value를 계산하고, 이를 통해 각 wire에 대해 실제 evaluation의 garbled value를 계산할 수 있습니다.
-
마지막 out wire에서는 translation table을 통해 실제 evaluation값을 얻습니다. 이를 Alice에게 보냅니다.
이를 도식으로 나타내면 다음과 같습니다.
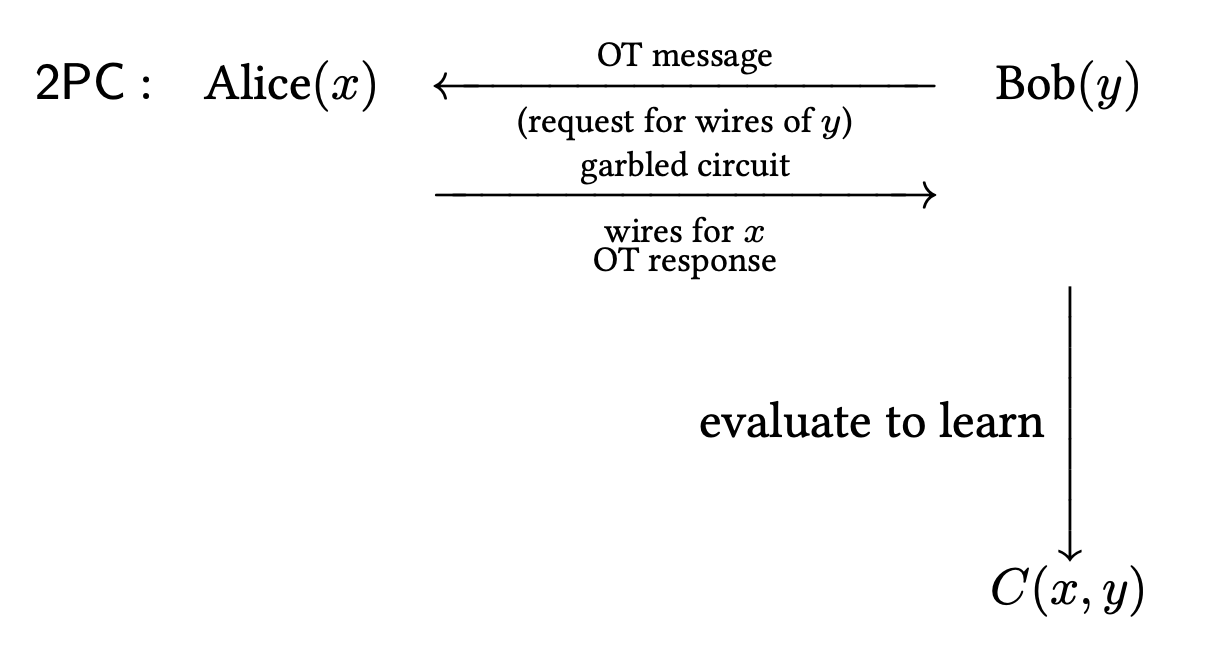
위 Protocol은 circuit size에 linear한 communication complexity를 가지며, round complexity는 $O(1)$입니다.
실제로 구현할 때는 $Enc$로 간단하게 AES 등을 이용할 수 있습니다.
Oblivious Transfer
앞에서 살펴보았듯이, Oblivious Transfer란 다음과 같은 프로토콜을 말합니다.
Setting: Alice가 값 $x_0, x_1$을 가지고 있고 Bob이 비트 $b$를 가지고 있습니다.
Goal: Bob이 $x_b$를 얻습니다.
Security: Alice는 $b$에 대한 정보를 얻지 못하고, Bob은 $x_{1-b}$에 대한 정보를 얻지 못합니다.
Oblivious Transfer에 대해서는 간력하게 어떻게 construct할 수 있는지만 살펴볼 것입니다.
OT protocol
Step 1.
group $G$의 원소 $g$ 가 order $q$를 가진다고 합시다.
Bob은 다음 값들을 generate합니다:
- $sk \leftarrow \mathbb{Z_q}, h = g^{sk}$
- $h’ \leftarrow G$
- $pk_b = h, pk_{1-b} = h’$
그 후 $(pk_0, pk_1)$를 Alice에게 보냅니다.
Step 2. Alice는 각 $x_i$를 $pk_i$를 이용해 encrypt하여 $c_i$를 얻고, 이를 Alice에게 전달합니다.
$\beta_0, \beta_1 \leftarrow \mathbb{Z}_q$
$c_0 = (g^{\beta_0}, H({pk_0}^{\beta_0} )\oplus x_0), c_1 = (g^{\beta_1}, H({pk_1}^{\beta_1}) \oplus x_1)$
단, $H$는 cryptographic hash function입니다.
Step 3. Alice는 $c_i$를 $sk$를 이용해 Decrypt합니다.
$c_b = (s, t)$라 할 때,
$H(s^{sk}) \oplus t = x_b$를 얻습니다. 한편, $c_{1-b}$에 대해서는 $pk_{1-b}$가 랜덤한 값인 $h’$이므로 어떤 정보도 얻지 못합니다.
Properties of OT
위에서 본 것처럼 $x_0, x_1$이 있을 때 $x_b$를 얻는 것을 1-out-of-2 oblivious transfer라 합니다.
일반적으로, $k$-out-of-$n$ oblivious transfer란 $x_0, x_1, \cdots x_{n-1}$이 있을 때 $Shuffle(x_{b_0}, x_{b_1}, \cdots x_{b_{k-1}})$을 얻는 것을 말합니다. $Shuffle$이 있는 것에서 알 수 있듯이, Bob은 각 $b_i$가 어떤 값에 대응되는지는 알 수 없어야 합니다.
다음은 알려진 사실입니다.
Lemma. 임의의 정수 $n \ge k$에 대해, 1-out-of-2 oblivious transfer를 이용해 $k$-out-of-$n$ oblivious transfer를 구성할 수 있다.
Exercise. Explicit하게 $k$-out-of-$n$ OT를 구성하시오.
이를 통해 다음과 같은 결과를 얻을 수 있습니다:
Theorem. 임의의 정수 $n \ge k$에 대해 $k$-out-of-$n$ OT가 가능하다면 임의의 boolean function $f$를 compute할 수 있다. 위 Lemma에 의해, 1-out-of-2 OT는 complete하다.
Proof. 함수 $f$가 $n$개의 비트를 input으로 갖는 boolean function이라 하자. 전체 $2^n$가지 input 중 output이 $1$인 input들의 집합을 $S$라 할 때, $\lvert S \rvert$-out-of-$2^n$ OT를 이용하면 함수 $f$를 evaluate할 수 있다.
물론, OT를 이용한 위와 같은 프로토콜은 input에 exponential하게 증가하는 cost를 가지므로 Yao’s protocol에 비교했을 때 practical하지 않습니다.
Functional Encryption
일반적으로, public key encryption은
-
$Setup(1^{\lambda}) \rightarrow (pk, sk)$ : 공개키 $pk$와 비밀키 $sk$를 생성
-
$Encrypt(pk, x) \rightarrow ct_x$: plaintext $x$를 암호화
-
$Decrypt(sk, ct_x) \rightarrow x$: ciphertext $ct_x$를 복호화
가 성립하는 scheme을 말합니다. 물론 사용하기 위해서는 여기에 security 조건이 붙어야 하겠지만, 기본적으로는 위와 같은 구성을 가집니다.
Functional encryption이란 이를 보다 일반화시킨 개념입니다.
Definition. functional encryption scheme은 다음과 같은 (randomized) fuunction들로 구성됩니다:
-
$Setup(1^{\lambda}) \rightarrow (mpk, msk)$: security parameter $\lambda$를 받아 master public key $mpk$, master secret key $msk$를 생성
-
$Encrypt(mpk, x) \rightarrow ct_x$: master public key로 plaintext $x$를 암호화하여 ciphertext $ct_x$를 리턴
-
$KeyGen(msk, f) \rightarrow sk_f$: master secret key와 함수 $f$를 가지고 functional key $sk_f$를 생성
-
$Decrypt(sk_f, ct_x) \rightarrow f(x)$: functional key $sk_f$와 ciphertext $ct_x$를 입력으로 받고, $f(x)$를 리턴
Functional Encryption(FE)은 굉장히 general한 개념으로, 위에서 말한 public key encryption의 경우 $f$가 identity function만으로 제한되었을 때로 생각할 수 있습니다.
Correctness.
FE scheme의 Correctness는 위 함수들이 잘 동작하는 것만 확인하면 충분합니다. 즉, 임의의 함수 $f$와 plaintext $x$에서
$ct_x \leftarrow Encrypt(mpk, x)$ , $sk_f \leftarrow KeyGen(msk, f)$에 대해
$Decrypt(sk_f, ct_x) = f(x)$가 성립해야 합니다.
Security.
FE scheme의 security를 간단하게 말하자면, Decryption으로 $f(x)$만 얻을 수 있고 그것으로 추측할 수 있는 정보를 제외하면 $x$에 대해 어떤 정보도 얻지 못해야 합니다는 것입니다.
엄밀한 정의를 하는 방법은 여러 가지가 있지만, 여기에서는 game-based security를 사용할 것입니다.
다음과 같은 security game을 생각해 봅시다:
Security Game of FE scheme.
-
Challenger와 Adversary $\mathcal{A}$가 있는 세팅입니다. 여기서 Challenger는 FE scheme의 보안을 증명하고 싶고, $\mathcal{A}$는 보안을 뚫는 역할로 볼 수 있습니다.
-
처음에 Challenger는 $Setup$으로 $mpk$와 $msk$를 생성하고, $mpk$를 $\mathcal{A}$에게 보냅니다.
-
$\mathcal{A}$는 다음과 같은 query를 polynomial times 할 수 있습니다:
- 함수 $f$를 골라 Challenger가 $sk_f \leftarrow KeyGen(msk, f)$를 계산하게 하여 $sk_f$를 받는다.
-
$\mathcal{A}$는 2번 과정에서 사용한 모든 함수 $f$에 대해 $f(x_0) = f(x_1)$을 만족하는 $x_0, x_1$을 찾아 이를 Challenger에게 보냅니다.
-
Challenger는 랜덤 비트 $b$에 대해 $ct_b \leftarrow$를 계산하여 $ct_b$를 $\mathcal{A}$에게 전달합니다.
-
$\mathcal{A}$는 2번 과정과 마찬가지로 함수 $f$를 골라 $sk_f$를 받는 쿼리를 polynomial times 할 수 있습니다. 단, $f(x_0)=f(x_1)$을 만족해야 합니다.
-
$\mathcal{A}$가 $b$에 대한 guess $b’$를 합니다.
어떤 Probabilistic Polynomial Time Adversary에 대해서도 $\lvert Pr[b’=b] - 1/2 \rvert$가 negligible할 때, 해당 FE scheme을 secure하다고 합니다.
FE using Garbled Circuit
앞서 살펴본 2-party computation using Garbled Circuit은 다음과 같은 프로토콜이었습니다.

한편, FE는 다음과 같은 형태여야 합니다.
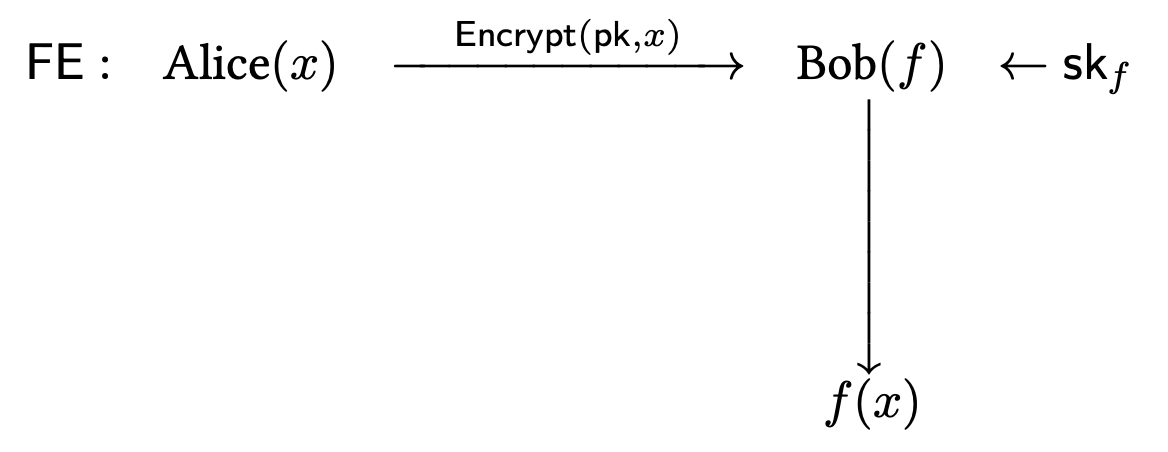
문제는 $f$가 Bob의 쿼리이기 때문에, Alice는 미리 garbled value를 계산할 수 없다는 점입니다.
이를 해결하기 위해 Universal circuit $U(C,x)$와 Restricted universal circuit $U_x(C)$가 사용됩니다. universal circuit $U(C,x) = C(x)$, restricted universal circuit $U_x(C) = C(x)$로 정의됩니다. circuit을 input으로 받으면 이때까지 boolean circuit의 정의와 다른 것이 아니냐는 물음이 있을 수 있지만, circuit $C$는 $O(\lvert C \rvert)$ bit에 인코딩할 수 있으므로 $U, U_x$는 모두 boolean circuit입니다.
먼저, query되는 $f$의 circuit representation $C$의 encoding이 $l$ 비트를 넘지 않는다고 합시다.
Theorem. 다음은 secure functional encryption이다.
-
- $mpk: pk_1^{(0)}, \cdots pk_l^{(0)}, pk_1^{(1)}, \cdots pk_l^{(1)}$
- $msk: sk_1^{(0)}, \cdots sk_l^{(0)}, sk_1^{(1)}, \cdots sk_l^{(1)}$
- $Encrypt(mpk, x):$
- $(\bar{U}, \{ L_i^{(b)} \}_{i \in [l], b \in \{ 0, 1 \} })$: Garbled circuit of $U_x$
- $ct_i^{(b)} \leftarrow Enc(pk_i^{(b)}, L_i^{(b)})$
-
$KeyGen(msk, C): sk_i^{(C_i)}$
- $Decrypt(sk_c, ct_x):$
- $L_i^{(C_i)} \leftarrow Dec(sk_i^{(C_i)}, ct_i^{(C_i)})$
- $y \leftarrow Eval(\bar{U}, \{ L_i^{(C_i)} \})$
이 프로토콜은 이해하기 어려울 수 있습니다. 간단히 circuit을 비트로 인코딩할 수 있으므로 universal circuit이나 restricted universal circuit 모두 일반적인 circuit으로 생각할 수 있고, 이를 이용하면 functional encryption이 가능하다 정도로 생각하시면 충분할 것 같습니다.
Conclusion
Garbled Circuit과 Oblivious Transfer, 그리고 Functional Encryption에 대해 알아보았습니다. 위에서 살펴본 functional encryption scheme은 circuit의 size에 linear한 communication이 필요한데, sublinear하게 하는 것도 가능하고, lattice cryptography를 이용해 construct할 수 있습니다. 이와 관련해서 흥미를 가지신 분은 UT Austin 강의의 Notes를 한번 읽어보시면 좋을 것 같습니다.
Reference
- [Notes] www.cs.utexas.edu/~dwu4/courses/sp22/static/scribe/notes.pdf
- 서울대학교 현대암호학 슬라이드 14장 secure multiparty computation
- 서울대학교 현대암호학 슬라이드 15장 garbled circuit