May 27, 2024 20:00

이 포스트에서는 이전 글인 Suffix Automaton으로 Suffix Array 문제들을 풀어보자 1에 이어서, Suffix Automaton과 함께 사용할 수 있는 여러 테크닉들에 대해 설명합니다. Suffix Automaton이 무엇인지에 대해서는 제 이전 글을 참고하셔도 좋고, 아래 글을 읽어보셔도 좋습니다.

• https://koosaga.com/314

• https://cp-algorithms.com/string/suffix-automaton.html

DAG + Small to Large

Suffix Automaton의 DAG에서 DP를 진행할 수도 있지만, 관리해야 하는 것이 어떤 값이 아닌 목록인 경우 Small to Large 테크닉을 활용할 수 있습니다.

DAG에서 Small to Large를 활용하게 되는 대표적인 경우는, $n$개의 문자열 $S_1, S_2, \cdots, S_n$이 주어질 때 어떤 문자열 $P$를 부분 문자열로 가지는 문자열 $S_i$들의 목록을 알고 싶은 경우입니다. 이는 많은 경우에 유용하게 쓰일 수 있습니다.

예를 들어, $n$개의 문자열 $S_1, S_2, \cdots, S_n$에 전부 포함된 공통 부분 문자열 중 가장 긴 것을 알고 싶다고 해봅시다.

이를 위해, $S_1+c_1+S_2+c_2+\cdots+S_n+c_n$을 Suffix Automaton에 집어넣는 방법을 생각할 수 있습니다. 이 때 $c_i$는 특수한 문자이며, 기존 문자열인 $S_i$에 등장하지 않고 또한 모든 $i, j$에 대해 $c_i \ne c_j$인 유일한 문자여야 합니다.

어떤 문자열 $P$가 모든 문자열 $S_1, S_2, \cdots, S_n$에 등장한다는 것은, Suffix Automaton의 DAG 상에서 그 문자열 $P$ 에 해당하는 상태로부터 다른 특수한 문자 $c_i$를 거치지 않고 직접 $c_1, c_2, \cdots, c_n$에 접근할 수 있어야 한다는 것과 동치입니다.

따라서 각 노드별로 다른 특수 문자 $c_i$를 거치지 않고 직접 접근 가능한 특수 문자들의 집합을 관리한다면, 집합의 크기를 통해 이 노드가 표현하는 문자열이 몇 개의 문자열에서 등장하는지 알 수 있고, 따라서 모든 노드를 순회하며 모든 문자열에 등장하는 가장 긴 공통 부분 문자열의 길이를 알 수 있게 됩니다.

구현은 아래와 같습니다. 아래 예시의 경우 문자를 int로 취급하고 각각의 특수 문자 $c_i$는 $c_1 = -1, c_2 = -2, \cdots, c_n = -n$처럼 음수로 정하였으며, 따라서 각 노드의 다음 노드를 나타내는 nxt는 배열이 아닌 map<int,int>로 구현되었습니다.

struct SuffixAutomaton {
	struct Node {
		int len, link
		map<int,int> nxt; // use map instead of array
		bool has(int c) { // use int instead of char
			return nxt.count(c);
		}
		int get(int c) { // use int instead of char
			return has(c) ? nxt[c] : 0;
		}
		void set(int c, int x) { // use int instead of char
			nxt[c] = x;
		}
		void copy(Node& o) {
			link = o.link;
			nxt = o.nxt;
		}
	};
	/* ... */
};

어떤 노드에서 직접 접근 가능한 특수 문자들의 집합을 구성하는 방법은 간단하게 떠올릴 수 있습니다.

어떤 노드에서 다음 문자가 특수 문자이면 (즉, 음수이면) 그 특수 문자를 현재 집합에 저장하고, 그렇지 않으면 다음 노드의 집합을 구해서 그 집합을 현재 상태의 집합에 합쳐줍니다. 즉, DP와 비슷한 방식으로 진행할 수 있습니다. 코드로 옮기면 아래와 같습니다.

set<int> s[N];
bool vis[N];
void dfs(int cur) {
	if(vis[cur]) return;
	vis[cur] = 1;
	for(auto& [c, nxt]:v[cur].nxt) {
		if(c < 0) s[cur].insert(c);
		else {
			dfs(nxt);
			for(int x:s[nxt]) s[cur].insert(x);
		}
	}
	// do something with current set
}	

그러나 이 경우, 각 상태마다 집합을 모두 구해서 저장하게 되므로 메모리와 시간 모두 초과하게 될 가능성이 높습니다.

따라서 Small to Large를 이용해서 메모리와 시간복잡도 모두 개선해줄 수 있습니다. 합쳐야 하는 다음 상태들의 집합들 중 가장 큰 것을 재사용하고, 그 곳에 나머지 집합들을 합쳐주는 방식으로 구현할 수 있습니다.

set<int> s[N];
bool vis[N];
void dfs(int cur) {
	if(vis[cur]) return;
	vis[cur] = 1;
	int mx = -1, idx = -1;
	
	for(auto& [c, nxt]:sa.v[cur].nxt) {
		if(c < 0) continue;
		dfs(nxt);
		if(mx < s[nxt].size()) {
			mx = s[nxt].size();
			idx = nxt;
		}
	}
	
	if(idx != -1) s[cur].swap(s[idx]);
	
	for(auto& [c, nxt]:sa.v[cur].nxt) if(nxt != idx) {
		if(c < 0) s[cur].insert(c);
		else for(int x:s[nxt]) s[cur].insert(x);
	}
	// do something with current set
}	

이 경우에도 마찬가지로 모든 상태를 순회하며 각 상태의 직접 접근 가능한 특수 문자 목록을 볼 수 있다는 점은 변하지 않지만, 이미 순회가 끝난 상태의 집합을 올바르게 유지한다는 보장이 없기 때문에, 정해진 순서대로만 봐야 한다는 제한이 생기게 됩니다.

[연습 문제] Substring Query (BOJ 19132)

$n$개의 문자열 $S_1, S_2, \cdots, S_n$이 주어지고, 각 쿼리마다 $(l, r, P)$가 주어지면 $S_l, S_{l+1}, \cdots, S_r$ 중 몇 개가 $P$를 부분 문자열로 가지는지 구해야 하는 문제입니다.

우선, 특수 문자 $c_i = -i$로 설정한 후 $S_1+c_1+S_2+c_2+\cdots+S_n+c_n$을 Suffix Automaton에 넣어줍니다.

또한, Small to Large를 이용하는 경우 원하는 순서대로 상태를 순회할 수 없기 때문에, 모든 쿼리를 읽은 다음 각 쿼리마다 $P$에 해당하는 상태를 찾아 Offline Query로 만들어줍니다.

그 다음, Small to Large로 합치면서 각 상태에서 직접 접근 가능한 특수 문자들의 목록을 구합니다. 어떤 상태 $v$에서 특수 문자 $c_i=-i$에 접근이 가능하다면, 이 상태 $v$가 표현하는 문자열은 $i$번째 문자열 $S_i$에 등장함을 의미합니다.

우리가 상태 $v$에 관한 쿼리 $(l,r)$에 대해 궁금한 것은 $S_l, S_{l+1}, \cdots, S_r$ 중 몇 개에 등장하는지이므로, 상태 $v$에서 도달 가능한 특수 문자들의 집합에서 $-r$과 $-l$ 사이의 값을 가지는 원소가 몇개 있는지를 구하면 해당하는 쿼리의 정답을 구할 수 있습니다.

집합에서 특정 값보다 작은 원소의 개수를 구하는 것은 기본 set에서는 지원하지 않는 기능이지만, pb_ds를 이용하면 $O(\log n)$의 시간복잡도로 간편하게 구할 수 있으므로 문제를 풀기에 충분합니다.

[연습 문제] 문자열 X (BOJ 23053)

$n$개의 문자열 $S_1, S_2, \cdots, S_n$이 주어질 때, 이들 중 정확히 $k$개에 등장하는 서로 다른 부분 문자열이 몇 개인지 세는 문제입니다.

따라서 우선 특수 문자 $c_i = -i$로 설정한 후 $S_1+c_1+S_2+c_2+\cdots+S_n+c_n$을 Suffix Automaton에 넣어줍니다.

그 다음, Small to Large로 합치면서 각 상태에서 직접 접근 가능한 특수 문자들의 목록을 구해줍니다. 우리가 관심 있는 것은 각 상태마다 직접 접근 가능한 특수 문자의 개수가 정확히 $k$인 것들이므로, 집합의 원소 개수가 $k$일 때만 해당 상태가 표현하는 문자열의 개수를 정답에 더해줍니다.

Suffix Automaton에 들어있는 문자열이 단일 문자열이 아닌 여러 문자열을 이어 붙인 것이므로, 해당 상태가 표현하는 문자열의 개수를 정확히 구하려면 추가적인 처리가 필요할 수 있습니다.

Suffix Link + DP

어떤 노드의 특정한 속성은 Suffix Link로부터 유도될 수 있습니다. 예를 들어, 특정 노드에 해당하는 $endpos$의 크기 $\vert endpos\vert $, 즉 특정 노드가 표현하는 부분 문자열이 전체 문자열에서 몇 번 등장하는지를 알고 싶다고 해봅시다. 어떤 노드 $v$에 대해 등장 횟수를 나타내는 속성을 $size$라고 해봅시다. $v.size$를 어떻게 구할 수 있을까요?

간단히 생각해봤을 때, $S$가 들어 있는 Suffix Automaton에 문자 $c$를 추가하면 전체 문자열 $Sc$의 모든 suffix들의 등장 횟수가 $1$씩 증가함을 알 수 있습니다. 이 작업은 $Sc$에 해당하는 노드 $v$의 Suffix Link를 타고 올라가며 만나는 모든 노드 $v, v.link, v.link.link, \cdots$의 $size$를 모두 $1$씩 증가시켜 줌으로써 해결할 수 있지만, 루트 노드까지 만나게 되는 Suffix Link의 개수는 최대 $O(n)$이기 때문에 Suffix Automaton에 문자를 추가할 때 마다 이 작업을 진행하면 시간 초과가 날 것입니다(문자열 $\rm{aaa\cdots a}$를 생각해 봅시다).

어떻게 이 과정을 더 빠르게 할 수 있을까요? 문자를 하나씩 넣으면서 업데이트하는 대신, 문자열 $S$를 Suffix Automaton에 모두 넣은 후에 작업을 진행한다고 생각해봅시다. 즉, offline으로 진행하는 것입니다.

$S$가 모두 Suffix Automaton에 들어있는 상황에서, 위의 과정은 $S$의 prefix를 나타내는 노드를 모두 찾은 후, 각 노드마다 Suffix Link 상에서 루트까지 타고 올라가며 만나는 모든 노드에 $size$를 $1$씩 더해주는 것과 동일합니다.

아래 그림은 $S=\rm{abcbc}$일 때의 Suffix Automaton에서 prefix를 나타내는 노드를 초록색으로 표시하고, Suffix Link에서 위 과정을 진행했을 때 각 노드의 $size$의 값을 표시한 그림입니다. 각 노드가 표현하는 부분 문자열이 $\rm{abcbc}$에서 몇 번 등장하는지 올바르게 구해짐을 볼 수 있습니다.

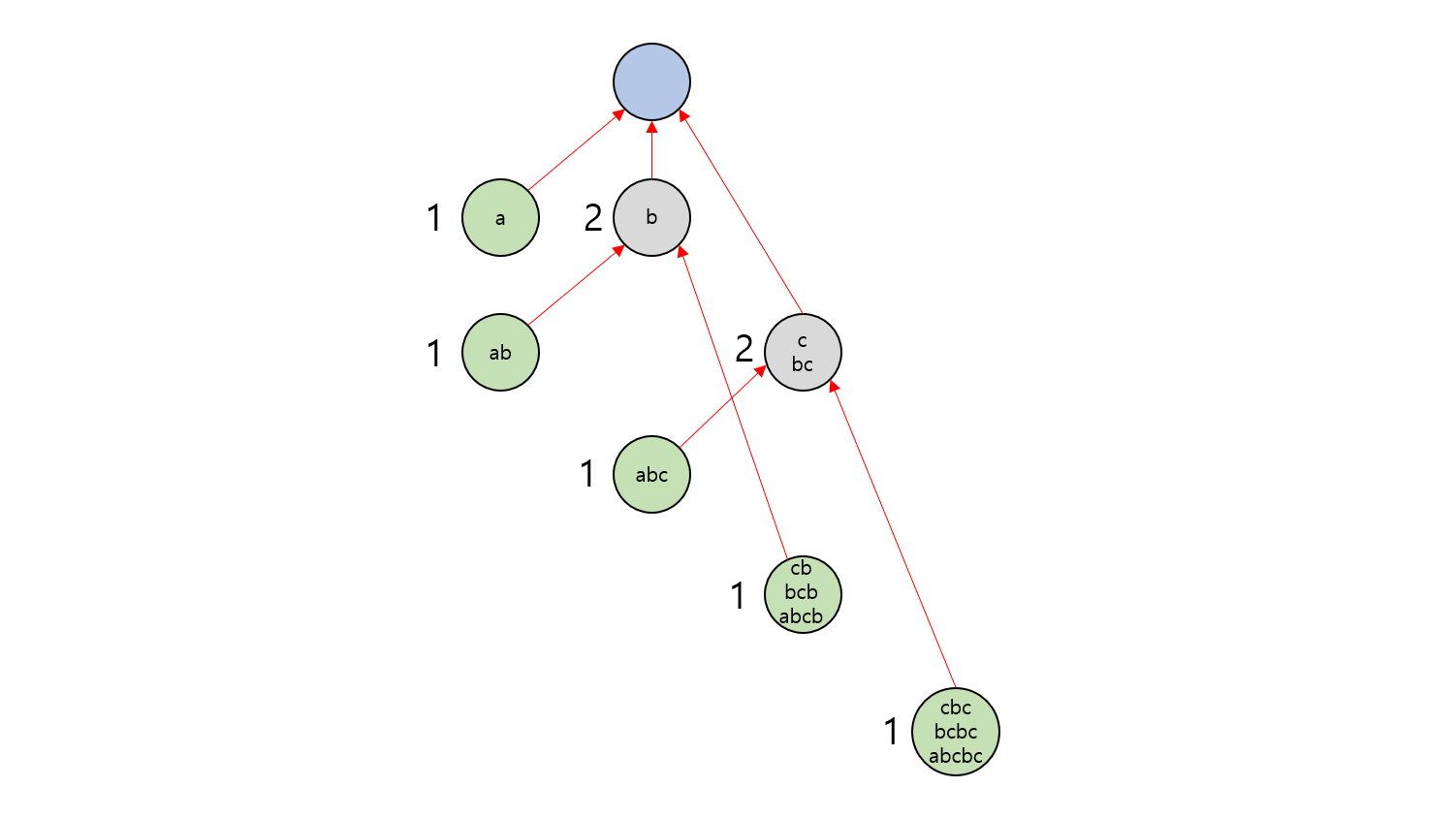
하지만 잘 생각해보면, 어떤 노드의 $size$는 Suffix Link에서 자신을 루트로 하는 서브트리 내에 존재하는 초록색 노드의 개수와 동일함을 알 수 있습니다. 이 사실은 위 그림에서 쉽게 확인할 수 있습니다.

이와 같이 서브트리와 관련된 값은 트리 DP를 이용하여 $O(n)$의 시간복잡도로 쉽게 구할 수 있습니다. 굳이 루트까지 Suffix Link를 타고 올라가며 모든 노드에 $1$씩 더하지 않아도 $size$의 값을 구할 수 있다는 것이죠.

Suffix Link는 노드의 부모 정보만 저장하고 있으므로, 노드의 자식들을 모두 구해서 실제 트리를 구축한 뒤 트리 DP를 진행할 수도 있겠지만, Suffix Link의 특성 상 트리를 구성하지 않고도 DP를 진행할 수 있습니다.

단순히 Suffix Automaton의 모든 노드를 $len$이 감소하는 순서로 정렬한 뒤, 순서대로 점화식 v.link.size += v.size를 적용해주면 됩니다. Suffix Link의 특성 상 $len$이 긴 노드부터 방문하면 위상 정렬 순서를 만족하기 때문입니다.

모든 노드를 $len$이 감소하는 순서로 정렬하는 것은 커스텀 정렬 함수를 이용하는 경우 $O(n \log n)$이지만, 모든 노드 $v$에 대해 $0 \le v.len \le n$이므로 Counting Sort를 이용하면 $O(n)$에 정렬할 수 있습니다.

따라서 전체 시간복잡도 $O(n)$에 DP를 진행해줄 수 있습니다.

아래는 각 노드가 표현하는 부분 문자열의 등장 횟수 size와 각 노드에 해당하는 끝점 집합 $endpos$의 원소 중 최댓값 max_pos를 DP로 구하는 예시 코드입니다. 기존 구현에서 추가된 부분은 주석으로 added라고 표시해 두었습니다.

struct SuffixAutomaton {
	struct Node {
		int len, link, nxt[26];
		int size, min_pos, max_pos; // added
		bool has(char c) {
			return nxt[c-'a'];
		}
		int get(char c) {
			return nxt[c-'a'];
		}
		void set(char c, int x) {
			nxt[c-'a'] = x;
		}
		void copy(Node& o) {
			link = o.link;
			memcpy(nxt, o.nxt, sizeof(nxt));
			max_pos = min_pos = o.min_pos; // added
		}
	};
	int head, tail;
	vector<Node> v;
	vector<int> t[N]; // added (for counting sort)
	int push_node() {
		v.push_back(Node());
		return v.size() - 1;
	}
	SuffixAutomaton() {
		push_node(); // dummy
		head = tail = push_node(); // root
	}
	void push(char c) {
		int cur = push_node();	
		v[cur].len = v[tail].len + 1;
		v[cur].link = head;
		v[cur].size = 1; // added
		v[cur].min_pos = v[cur].max_pos = v[cur].len - 1; // added
		int p = tail;
		while(p && !v[p].has(c)) v[p].set(c, cur), p = v[p].link;
		if(p) {
			int q = v[p].get(c);
			if(v[p].len + 1 == v[q].len) v[cur].link = q;
			else {
				int clone = push_node();
				v[clone].copy(v[q]);
				v[clone].size = 0; // added
				v[clone].len = v[p].len + 1;
				v[cur].link = v[q].link = clone;
				while(p && v[p].get(c) == q) v[p].set(c, clone), p = v[p].link;
				t[v[clone].len].push_back(clone); // added
			}
		}
		tail = cur;
		t[v[cur].len].push_back(cur); // added
	}
	void get_dp() { // added
		for(int i=v[tail].len;i>0;i--) for(int x:t[i]) {
			v[v[x].link].size += v[x].size;
			v[v[x].link].max_pos = max(v[v[x].link].max_pos, v[x].max_pos);
		}
	}
};

[연습 문제] 문자열 함수 계산 (BOJ 12917)

각 노드 $v$ 가 표현하는 문자열의 최대 길이 $v.len$은 Suffix Automaton을 구성하게 되면 이미 알고 있고, 문자열의 등장 횟수 $v.size$만 구해준다면 답을 구할 수 있습니다.

위에서 설명한 것 처럼, $S$의 prefix에 해당하는 노드의 $size$를 $1$로 설정하고, 모든 노드를 $len$이 감소하는 순서대로 정렬한 뒤 v.link.size += v.size의 점화식을 적용해주면 각 상태의 부분문자열 등장 횟수 $v.size$를 올바르게 구할 수 있습니다.

모든 노드 $v$의 $v.size$를 모두 구한 이후에는, 단순히 모든 노드를 순회하면서 $v.len \times v.size$의 최댓값을 구해주면 됩니다.

DP로 $size$를 구해주는 것이 $O(n)$, 모든 노드를 순회하는 것도 $O(n)$이기에 전체 시간복잡도는 $O(n)$입니다.

[연습 문제] 좋은 부분 문자열 (BOJ 13432)

문자열에서 겹치지 않게 두 번 이상 등장하는 서로 다른 부분 문자열의 개수를 세는 문제입니다.

등장 횟수는 위에서처럼 $size$를 구하면 알 수 있지만, 서로 겹치는지 아닌지는 실제 등장 위치가 어디인지 알아야, 즉 각 노드별로 $endpos$ 집합에 대한 정보를 가지고 있어야 알 수 있습니다.

생각해보면, 한 노드가 표현하는 부분 문자열들 중 겹치지 않고 두 번 등장하는 것들을 모두 찾으려면 가장 처음 등장 위치와 가장 마지막 등장 위치만 알아도 충분합니다. 어떤 노드에 해당하는 $endpos$ 집합에서 가장 작은 것을 $minpos$, 가장 큰 것을 $maxpos$라고 합시다. 그러면 어떤 노드 $v$가 표현하는 부분 문자열들 중에서 서로 겹치지 않게 늘릴 수 있는 최대 길이는 $v.maxpos - v.minpos$가 됨을 알 수 있습니다.

어떤 노드 $v$가 표현하는 부분 문자열들의 개수는 $v.len - v.link.len$라는 것을 기억하시나요? 어떤 노드 $v$가 표현하는 부분 문자열들의 길이가 구간 $(v.link.len, v.len]$에 속하기 때문입니다. 그런데 우리는 여기에 속하는 부분 문자열들 중 길이가 $v.maxpos-v.minpos$보다 작은 것만을 세기를 원합니다.

따라서, 각 노드가 표현하는 부분 문자열들 중 겹치지 않고 등장하는 것들의 개수는 $\max(0, \min(v.len, v.maxpos-v.minpos) - v.link.len)$처럼 구해줄 수 있습니다.

이제 남은 것은 모든 노드 $v$에 대해 $v.minpos$와 $v.maxpos$를 구해주는 것입니다. $minpos$는 Suffix Automaton을 구성하는 과정을 살짝만 수정하면 쉽게 구해줄 수 있습니다. 그러나 $maxpos$의 경우, $size$를 구할 때와 비슷한 문제가 발생합니다.

문자열 $S$가 들어있는 Suffix Automaton에 문자 $c$를 추가하면, $Sc$의 모든 suffix들의 $maxpos$가 $\vert S\vert $로 업데이트되어야 합니다. $c$가 추가된 위치가 $Sc$의 모든 suffix들의 마지막 등장 위치가 되었기 때문이죠. 그러나 $Sc$의 Suffix Link를 루트까지 따라 올라가면서 만나는 모든 노드의 $maxpos$를 업데이트해주는 것은 너무 많은 시간이 듭니다.

따라서 $maxpos$를 $size$의 경우와 같이 DP를 이용해 효율적으로 구해줄 수 있습니다. 우선 모든 노드 $v$의 $v.maxpos$를 $v.minpos$로 초기화 해놓고, 모든 노드를 $len$이 감소하는 순서대로 정렬한 뒤 v.link.maxpos = max(v.link.maxpos, v.maxpos)의 점화식을 적용해주면 각 상태 $v$의 $endpos$의 최댓값 $v.maxpos$를 올바르게 구할 수 있습니다.

$minpos$와 $maxpos$를 모두 구한 후에는, 모든 노드 $v$를 순회하며 $\max(0, \min(v.len, v.maxpos-v.minpos) - v.link.len)$값을 모두 더해주면 정답을 구할 수 있습니다.

마찬가지로 시간복잡도는 $O(n)$입니다.

Suffix Link + Sparse Table

$S$로 Suffix Automaton을 구성했을 때, Suffix Automaton에서 $S$의 부분 문자열 $S[l..r]$에 해당하는 노드(상태)를 찾고 싶다고 합시다.

먼저 Suffix Automaton의 DAG를 이용하는 경우, 루트부터 시작해서 각각의 문자 $S[l], S[l+1], \cdots, S[r]$에 해당하는 transition을 순서대로 따라가면 $S[l..r]$에 해당하는 상태로 이동할 수 있을 것입니다. 그러나 이 경우 $r-l+1$ 번의 작업이 필요하게 되며, 최악의 경우 $O(n)$의 시간복잡도를 가지게 됩니다.

더 효율적으로 $S[l..r]$에 해당하는 상태를 찾기 위해, DAG 대신 Suffix Link를 이용할 수 있습니다.

먼저 $S$의 모든 prefix에 해당하는 상태들을 모두 전처리해놓습니다. 배열 $pref$를 만들고 $pref[i]$를 $S[0..i]$에 해당하는 노드의 번호(혹은 포인터)로 정의하면, $S[0..r]$에 해당하는 상태 $pref[r]$을 $O(1)$에 찾을 수 있습니다.

이제 우리가 원하는 $S[l..r]$은 $S[0..r]$의 suffix이므로, Suffix Link 상에서 $pref[r]$의 조상 중에 $S[l..r]$에 해당하는 노드가 존재합니다. 우리가 원하는 것은 특정 길이를 가진 부분 문자열을 찾는 것이므로, $pref[r]$의 조상 $v$ 중에서 $r-l+1 \in (v.link.len, v.len]$을 만족하는 $v$를 찾아야 합니다.

그런데 Suffix Link를 타고 올라갈 때마다 $len$이 감소하는 특성을 가지고 있으므로, 이분 탐색을 활용한다면 해당 조건을 만족하는 노드를 $O(\log n)$에 찾을 수 있음을 알 수 있습니다.

이분 탐색과 유사한 아이디어를 활용하기 위해, Suffix Link 상에 Sparse Table을 구성할 수 있습니다. $par[j][i]$를 번호가 $i$인 노드에서 $2^j$번 Suffix Link를 타고 이동하면 도착하는 노드의 번호로 정의하면 $O(n \log n)$에 $par$ 배열을 모두 채울 수 있습니다. 또한, Sparse Table의 아이디어를 그대로 활용하여 특정 조건을 만족하는 노드를 $O(\log n)$에 찾을 수 있습니다.

아래는 위의 SuffixAutomaton 구조체에서 위의 과정을 구현한 예시입니다. get_par()는 Sparse Table을 초기화하는 함수이며, locate(l, r)은 $S[l..r]$에 해당하는 노드 번호를 반환하는 함수입니다. get_par()는 Suffix Link의 구성이 완료된 후 호출하여야 하며, locate(l, r)은 get_par()의 호출 이후 사용하여야 합니다.

struct SuffixAutomaton {
	/* ... */
	vector<int> pref;
	int par[18][N];
	/* ... */
	void get_par() {
		for(int i=1;i<v.size();i++) par[0][i] = v[i].link;
		for(int j=1;j<18;j++) for(int i=1;i<v.size();i++) par[j][i] = par[j-1][par[j-1][i]];
	}
	int locate(int l, int r) {
		if(r < l) return head;
		int cur = pref[r];
		for(int i=17;i>=0;i--) if(v[v[par[i][cur]].link].len >= r - l + 1) cur = par[i][cur];
		while(v[v[cur].link].len >= r - l + 1) cur = par[0][cur];
		return cur;
	}
};

또, Sparse Table은 특정 부분 문자열에 해당하는 상태를 찾는 것 이외에도 Suffix Link 상에서 다른 작업을 하는 데에 유용하게 활용할 수 있습니다. 예를 들어, Suffix Link 상에서 두 노드의 Lowest Common Ancestor(LCA)를 구하면 두 문자열의 Longest Common Suffix를 $O(\log n)$에 구할 수 있습니다(Suffix Link의 의미를 생각해보면 쉽게 알 수 있습니다).

[연습 문제] Prefix-free Queries (BOJ 19332)

문자열 $S$가 주어지고 각 쿼리마다 $(l_1, r_1), (l_2, r_2), \cdots, (l_k, r_k)$가 주어지면, $k$개의 문자열 $S[l_1.. r_1], S[l_2..r_2], \cdots, S[l_k..r_k]$로 이루어진 목록에서 일부를 뽑는($0$개 혹은 $k$개를 뽑아도 됨) $2^k$개의 방법 중 어떤 것도 다른 것의 prefix가 아니게 되는 집합(prefix-free set)이 되도록 뽑는 방법의 개수를 구하는 문제입니다.

Suffix Link는 suffix를 관리하는 구조이므로, 일반성을 잃지 않고 임의로 어떤 것도 다른 것의 suffix가 되지 않는 집합(suffix-free set)이 되도록 하는 방법의 수를 생각해봅시다. 이 경우, 문자열 $S$를 뒤집어서 넣고 쿼리의 $(l,r)$도 뒤집은 문자열에 맞추어 적당히 변환해주면 원래의 prefix-free set이 되는 방법의 개수를 구하는 것과 동치가 됩니다.

먼저 문자열 $S$를 Suffix Automaton에 넣고 Suffix Link를 만들어봅시다. 어떤 부분 문자열들을 suffix-free set이 되도록 뽑는다는 것은, Suffix Link에서 조상-자손 관계에 있는 두 노드를 동시에 뽑지 않는다는 것입니다.

따라서, $k$개의 부분 문자열 $S[l_1.. r_1], S[l_2..r_2], \cdots, S[l_k..r_k]$에 해당하는 노드 번호를 Suffix Link + Sparse Table을 이용하여 $O(k \log n)$에 모두 찾은 후, 트리 압축을 이용하여 Suffix Link에서의 조상-자손 관계를 유지하며 $O(k)$개의 노드를 가지는 트리로 압축합니다. 압축된 트리에서 조상-자손 관계에 있는 두 노드를 동시에 뽑지 않는 방법의 개수는 트리 DP를 이용하여 $O(k)$에 구해줄 수 있습니다.

위 알고리즘을 이용하면 쿼리당 $O(k \log n)$에 처리 가능하며, 전체 시간 복잡도는 $O(\sum{k} \cdot \log n)$이 되어 문제를 풀 수 있게 됩니다. 다만 이 문제의 경우 Suffix Automaton + Sparse Table + 트리 압축을 이용하면 시간 제한이 매우 빡빡하므로 유의하시기 바랍니다.

Suffix Link + HLD

Suffix Automaton에서 각 노드의 $size$, $maxpos$와 같은 특정 속성은 DP를 통해 구할 수 있다고 하였습니다. 그러나 예를 들어, 다음 두 종류의 쿼리를 처리해야 한다면 어떻게 해야 할까요?

• 문자열에 마지막에 문자 $c$ 추가
• 문자열에서 어떤 문자열 $P$가 등장하는 횟수 출력

DP를 이용해서 구하는 경우, 전체 문자열을 넣은 이후 offline으로 처리하여 값을 구해야 하기 때문에, 위처럼 문자를 추가하는 도중에 online으로 $size$와 같은 값을 구할 수 없게 됩니다.

online으로 값을 관리하려면 글자 하나를 추가할 때 Suffix Link를 타고 올라가면서 전부 업데이트해줘야 하는데, 이는 최악의 경우 $O(n)$의 시간복잡도가 걸린다고 언급하였습니다.

그런데 이러한 종류의 업데이트는, Suffix Link로 이루어진 트리 상에서 어떤 노드과 루트 사이를 잇는 경로에 속하는 모든 정점들의 값을 전부 업데이트하게 됩니다. 즉, 본질적으로 트리 상에서 특정 경로에 포함된 모든 정점을 업데이트 하는 것입니다.

따라서, Heavy Light Decomposition(HLD)와 함께 구간 업데이트가 가능한 자료구조를 사용하면 해당 쿼리를 효율적으로 처리해줄 수 있습니다.

HLD와 함께 구간 업데이트에 Lazy Propagation을 지원하는 Segment Tree를 사용하는 경우, 어떤 노드로부터 루트까지 Suffix Link를 타고 올라가며 만나는 모든 노드의 값을 업데이트하는 과정이 더이상 $O(n)$이 아닌 $O(\log^2n)$에 가능해집니다. 따라서 매우 효율적으로 원하는 값을 관리할 수 있게 됩니다.

HLD를 이용하면 DP로 구해야 하는 값을 online으로 구할 수 있는 것처럼 보이지만, 사실 HLD도 Suffix Automaton에 전체 문자열 $S$를 넣고 난 이후에 Suffix Link에 구성해주어야 하는 것이므로 여전히 offline 알고리즘임은 변하지 않습니다. Suffix Link의 연결 상태가 변하는 과정도 online으로 관리하기 위해서는 Link-Cut Tree와 같은 다른 자료구조가 필요합니다.

[연습 문제] New Occurrences (BOJ 19299)

문자열의 맨 뒤에 문자가 하나씩 추가될 때마다, 문자열의 모든 서로 다른 부분 문자열의 등장횟수의 제곱의 합을 구해서 출력하는 문제입니다.

문자열 $S$의 맨 뒤에 문자 $c$가 추가되면, $Sc$의 모든 suffix들의 등장 횟수가 1씩 증가합니다. 따라서, $Sc$에 해당하는 노드의 Suffix Link를 타고 올라가면서 만나는 모든 노드의 등장 횟수를 1씩 늘려줘야 합니다.

이는 특정 노드부터 루트까지 이동하는 경로에 있는 모든 노드에 등장 횟수를 1씩 늘려주는 것과 동일하므로, Suffix Link에 HLD를 구성하고 Lazy Propagtion을 지원하는 세그먼트 트리를 사용하면 $O(\log^2 n)$에 해당 쿼리를 처리할 수 있습니다.

이제 남은 것은 모든 서로 다른 부분 문자열의 등장 횟수 제곱의 합을 구하는 것인데, 이는 세그먼트 트리의 각 노드에서 원소의 합과 원소의 제곱의 합을 관리하고 Lazy Propagation을 잘 구현해주면 어렵지 않게 할 수 있습니다.

따라서 위와 같은 자료구조를 세팅한 뒤, $S$의 prefix $S[0..i]$에 해당하는 노드 번호를 $pref[i]$에 전처리해놓았다면 아래와 같은 과정으로 문제를 풀 수 있습니다.

• $pref[0]$부터 루트까지 가는 경로에 모두 1씩 증가시킨 후, 제곱의 합 출력
• $pref[1]$부터 루트까지 가는 경로에 모두 1씩 증가시킨 후, 제곱의 합 출력
• $pref[2]$부터 루트까지 가는 경로에 모두 1씩 증가시킨 후, 제곱의 합 출력
• $\cdots$
• $pref[n-1]$부터 루트까지 가는 경로에 모두 1씩 증가시킨 후, 제곱의 합 출력

각각의 작업의 시간복잡도가 $O(\log^2 n)$이므로, 전체 시간복잡도 $O(n\log^2n)$에 문제를 풀 수 있습니다.

마치며

Suffix Automaton과 다른 알고리즘을 함께 사용하여 문제를 푸는 테크닉에 대해 알아보았습니다. 위에서 보듯이 Suffix Automaton으로 편하게 풀 수 있는 문제들의 커버리지가 꽤나 넓기 때문에, 저는 개인적으로 Suffix Automaton이 Suffix Array의 훌륭한 대안이 될 수 있다고 생각합니다. 저는 앞으로도 웬만한 문자열 문제는 먼저 Suffix Automaton으로 풀게 될 것 같습니다.

이 글에서는 풀이를 설명하지 않았지만, 아래의 문제들도 Suffix Array 없이 Suffix Automaton을 이용하여 해결하였으므로, 관심이 있으신 분들은 아래의 문제들을 Suffix Automaton으로 풀어보셔도 좋을 것 같습니다.

• https://www.acmicpc.net/problem/22905

• https://www.acmicpc.net/problem/18744

• https://www.acmicpc.net/problem/27525

• https://www.acmicpc.net/problem/25546

• https://www.acmicpc.net/problem/22349

• https://www.acmicpc.net/problem/15454

마지막으로, 긴 글 읽어주셔서 감사합니다.