Run Enumerate로 문제를 풀어보자
이 포스트는 Run Enumerate의 구현 및 활용에 대해 다루며, koosaga님의 포스트를 기반으로 쓰여졌습니다. 이 글에서는 Run Enumerate를 문제 풀이에 활용하는 방법을 위주로 다루며, 증명이나 기타 자세한 내용에 대해서는 다루지 않으므로 다른 글을 참고하시길 부탁드립니다.
Run Enumerate란?
Run Enumerate는 문자열 내부에 연속하여 존재하는 모든 반복 또는 반복의 일부를 찾고 싶을 때 쓰는 알고리즘입니다.
예를 들어, $\rm{mississippi}$라는 문자열을 생각해봅시다. 이 문자열에는 어떤 반복이 존재할까요? 한번 나열해 봅시다.
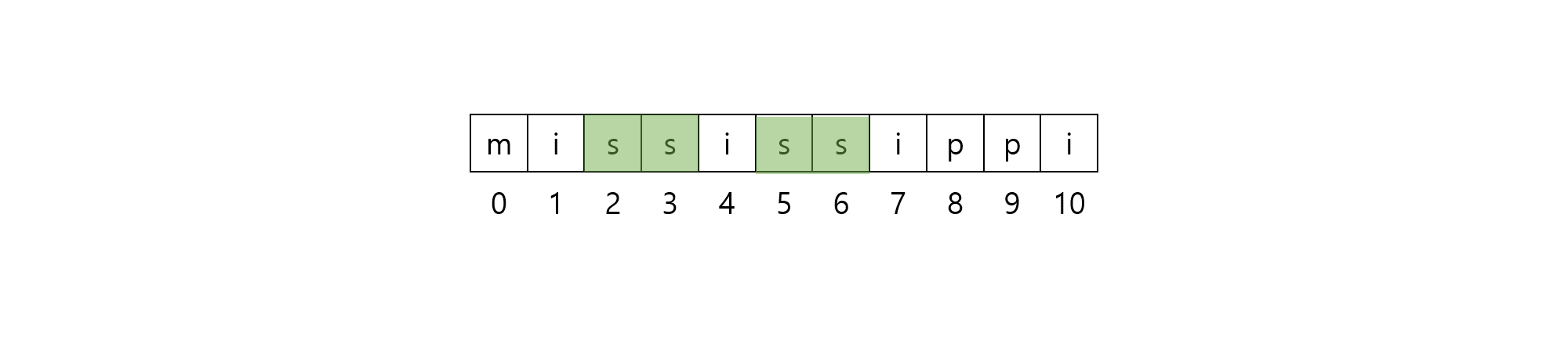
$[2, 4)$ 구간과 $[5,7)$ 구간에 해당하는 부분 문자열은 $\rm{ss}$로, 길이 $1$의 문자열 $\rm{s}$가 반복해서 나타납니다.
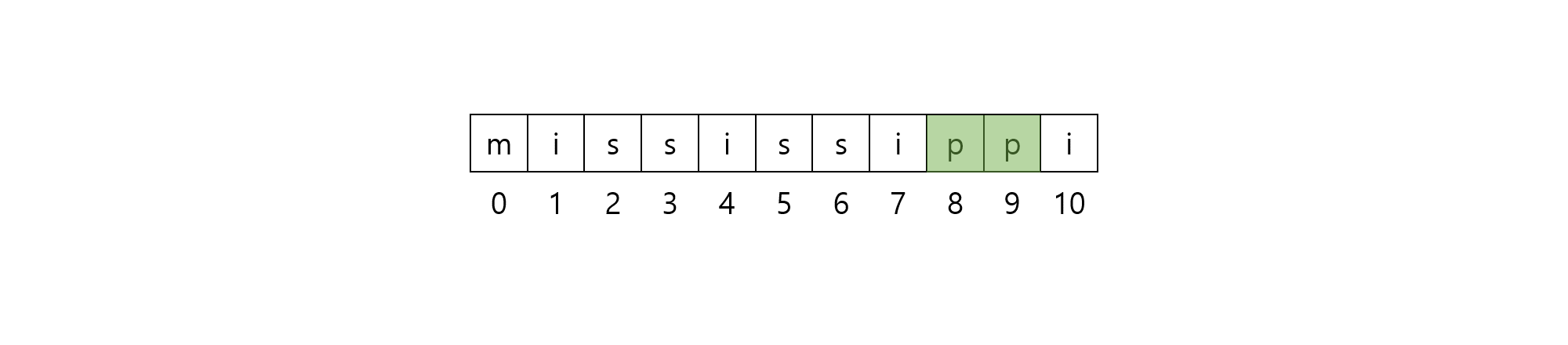
$[8, 10)$ 구간에 해당하는 부분 문자열은 $\rm{pp}$로, 길이 $1$의 문자열 $\rm{p}$가 반복해서 나타납니다.
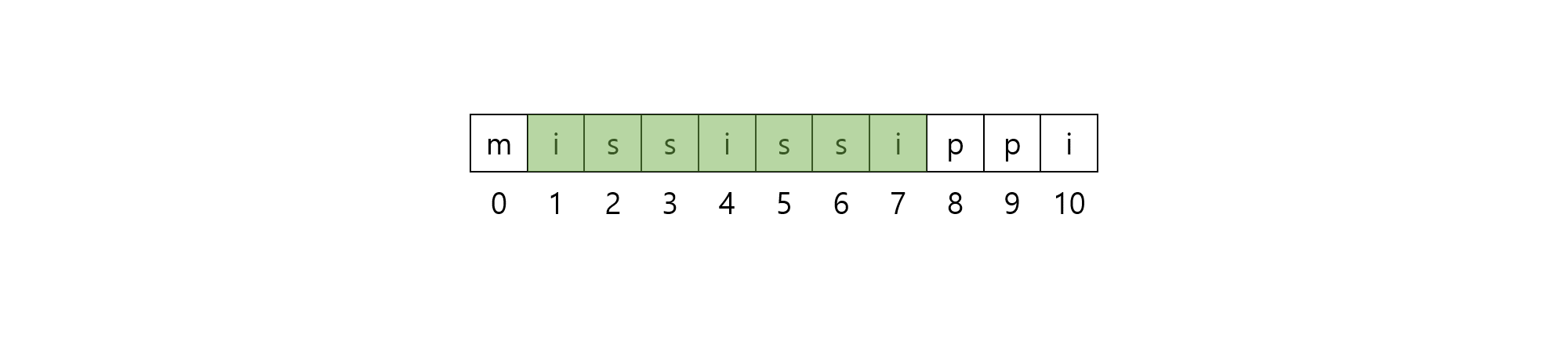
$[1, 8)$ 구간에 해당하는 부분 문자열은 $\rm{ississi}$로, 길이 $3$의 문자열 $\rm{iss}$가 반복해서 나타납니다. 이 때, 마지막 문자인 $\rm{i}$는 $\rm{iss}$의 일부만 반복된 것으로, 구간이 완전히 반복되지 않아도 찾는 것을 목표로 합니다. 이처럼, 완전한 반복이 아닌 반복 역시 반복이라고 표현하도록 하겠습니다.
위에서 보듯이, 문자열에 존재하는 모든 반복은 반복이 나타나는 구간 $[l,r)$과 그 때의 반복되는 문자열의 길이 $p$를 나타내는 튜플 $(l,r,p)$로 표현할 수 있습니다. 이러한 튜플 $(l,r,p)$ 중 특수한 조건을 만족하는 것을 문자열의 run이라 부르고, 이러한 run을 모두 찾는 알고리즘이 Run Enumerate입니다.
run이란?
문자열 $S$가 주어질 때, run은 다음의 조건을 모두 만족하는 튜플 $(l,r,p)$입니다.
- $0 \le l < r \le \vert S \vert$
- $1 \le p \le \vert S \vert $
- $r-l \ge 2p$
- $p$는 모든 $l \le i < r-p$에 대해서 $S[i] = S[i+p]$를 만족해야 하며, 가능한 $p$가 여러개라면 그 중 가장 작은 것이어야 합니다.
- 위의 네 조건이 $(l-1,r,p)$와 $(l,r+1,p)$에 대해서는 성립하지 않아야 합니다.
각각의 조건에 대해서 자세하게 살펴봅시다.
- $0 \le l < r \le \vert S \vert$
- $1 \le p \le \vert S \vert$
위 조건들은 문자열의 범위에 따른 기본적인 조건들입니다.
- $r-l \ge 2p$
위 조건은 구간 내에서 같은 문자열이 최소한 2번은 반복되어야 함을 의미합니다. 즉, $\rm{abcabca}$는 run으로 취급되지만 $\rm{abcab}$는 run으로 취급되지 않습니다.
- $p$는 모든 $l \le i < r-p$에 대해서 $S[i] = S[i+p]$를 만족해야 하며, 가능한 $p$가 여러개라면 그 중 가장 작은 것이어야 합니다.
위 조건은 구간 내에서 반복되는 문자열의 주기가 $p$여야 하며, 또한 $p$가 반복의 가능한 최소 단위여야 함을 의미합니다.
예를 들어 $S=\rm{aaaaaa}$인 경우 $S$는 $\rm{a}$의 반복이지만, $\rm{aaa}$의 반복으로 볼 수도 있고 $\rm{aa}$의 반복으로도 볼 수 있습니다. 즉, $S[i]=S[i+p]$를 만족하는 $p$가 $1$이 될 수도 있고 $2,3$이 될 수도 있습니다.
이 때, 가장 작은 $p$만 알고 있어도 충분하기 때문에 (나머지 반복들은 결국 가장 작은 $p$의 배수가 됩니다) run에는 가장 작은 $p$를 포함하도록 합니다.
- 위의 네 조건이 $(l-1,r,p)$와 $(l,r+1,p)$에 대해서는 성립하지 않아야 합니다.
위 조건은 $p$를 주기로 반복이 일어나는 구간 $[l, r)$이 최대한으로 넓어야 함을 의미합니다.
예를 들어, $\rm{mississippi}$의 경우 구간 $[1, 7)$은 $p=3$인 반복이 일어나기는 합니다.
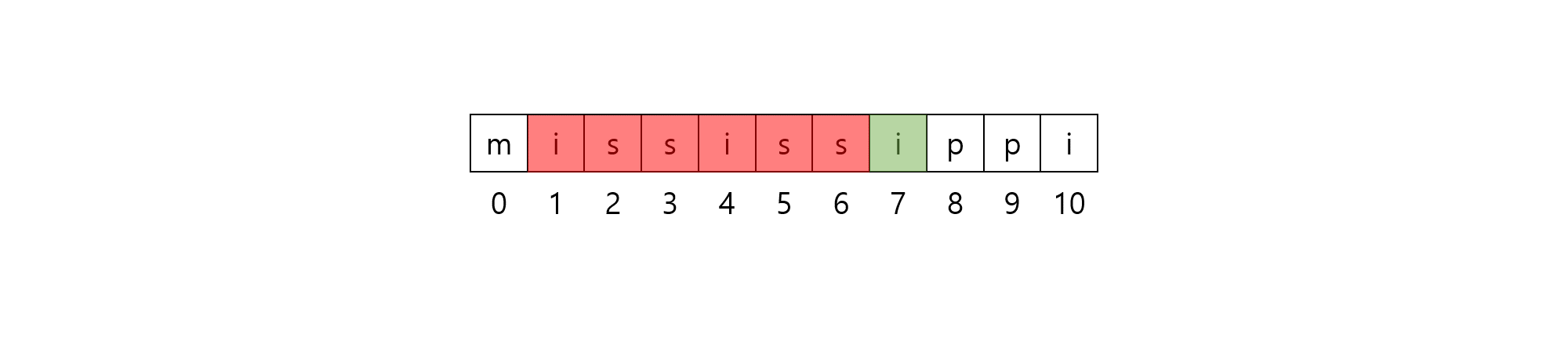
하지만, 반복되는 구간을 $[1, 8)$로 더 늘릴 수 있으므로 구간 $[1,7)$은 run으로 취급되지 않습니다.
이렇게 위 조건들을 모두 만족하는 run들을 나열하면, 문자열 내부에 존재하는 모든 반복을 중복 없이, 그리고 전부 나열할 수 있게 됩니다.
$S=\rm{mississippi}$인 경우, $S$에 존재하는 모든 run을 나열한 결과는 아래와 같습니다.
- $(2,4,1)$
- $(5,7,1)$
- $(8,10,1)$
- $(1,8,3)$
이와 같이, 문자열에 존재하는 모든 run을 찾는 것이 Run Enumerate 알고리즘입니다.
run의 특성
run을 찾는 것은 문자열에 존재하는 반복을 모두 찾는다는 점에서도 의미가 있지만, run 자체에도 문제 풀이에 유용한 여러가지 강력한 특성들이 존재합니다.
문자열 $S$의 길이를 $n$이라 하면, $S$의 run들에 대해서 아래의 성질들이 성립합니다.
- run의 개수는 $n$개를 넘지 않는다.
- 모든 run에 대해 $(r-l)/p$의 합은 $3n$을 넘지 않는다.
1번 성질은 존재하는 모든 run을 저장하고 읽는 것에 대한 복잡도를 $O(n)$으로 보장해줍니다. 즉, 우리는 항상 존재하는 모든 run의 complete한 목록을 저장하고 읽을 수 있습니다. 따라서 많은 경우, 일단 run의 목록만 구해 놓으면 실제로 그것을 이용해서 문제를 푸는 과정은 비교적 매우 간단합니다.
2번 성질은 존재하는 모든 반복을 찾을 때 유용합니다. 어떤 run $(l,r,p)$에서의 $p$는 반복의 최소 단위를 의미하기 때문에, 실제로 이 run에는 길이 $p$의 반복, 길이 $2p$의 반복, 길이 $3p$의 반복, $\cdots$이 모두 존재합니다.
예를 들어, $\rm{abababababab}$를 표현하는 run $(0, 12, 2)$의 내부에는
- 길이 $2$의 반복 $\rm{ab \vert ab}$ 혹은 $\rm{ba \vert ba}$
- 길이 $4$의 반복 $\rm{abab \vert abab}$ 혹은 $\rm{baba \vert baba}$
- 길이 $6$의 반복 $\rm{ababab \vert ababab}$
모두 존재함을 알 수 있습니다.
따라서, 가능한 모든 반복을 보기 위해서는 구간의 길이 $r-l$보다 작은 $p$의 배수를 모두 고려해주어야 합니다. 따라서, 각 run마다 최대 $(r-l)/p$개의 반복을 고려해주게 됩니다.
그러나, 2번 성질에 따르면 모든 run에 대해 $(r-l)/p$의 합은 $3n$을 넘지 않으므로, 모든 run에 대해 가능한 모든 $p$의 배수를 계산하더라도 시간복잡도는 여전히 $O(n)$이 보장됩니다.
따라서, 존재하는 모든 반복에 대해 계산하더라도 시간복잡도가 $O(n)$으로 보장된다는 강력한 성질입니다.
1번 성질과 2번 성질에 대한 증명은 이 논문에서 찾을 수 있다고 합니다.
추가적으로, 엄밀하지는 않지만 다음과 같은 사실을 관찰할 수 있습니다.
- run은 서로 잘 겹치지 않는다.
최대한 많은 run이 겹치도록 하는 문자열을 손으로 직접 구성해 봅시다. run이 되려면 최소한 2번의 반복이 있어야 한다는 사실을 잊지 마세요!
여러분들이 저와 비슷한 생각을 하셨다면, $\rm{aabaabcaabaabc}$와 유사한 문자열을 시도하셨을 것입니다.
하나 알 수 있는 사실은, 문자열의 길이를 늘리지 않고서 run을 최대한 많이 겹치기는 어렵다는 것입니다. 결국 겹치는 run의 개수가 하나 늘어날 때, 문자열의 길이는 $2$배 정도 늘어나는 경향이 있다는 것을 관찰하실 수 있을 것입니다.
따라서, 다음과 같은 사실을 문제 풀이에 사용할 수 있습니다.
- 문자열 $S$의 한 문자 $S[i]$가 속하는 서로 다른 run의 개수는 매우 적다.
위에서 관찰했듯이 겹치는 run이 하나 늘어나려면 문자열의 길이는 $2$배 정도 늘어나야 하기 때문에, 실제로 한 문자가 속할 수 있는 서로 다른 run의 개수는 최악의 경우에도 $O(n)$이 아닌 $O(\log n)$개라고 저는 추측합니다.
위 사실을 증명하지는 못했지만, 대충 $O(\log n)$이라 가정하고 문제를 풀었을 때에도 시간 초과가 발생하지 않았습니다. 따라서, 증명은 없지만 문제풀이에 충분히 사용 가능한 수준이라고 저는 추측하고 있습니다.
Run Enumerate 구현
그렇다면 실제로 어떻게 Run들을 효율적으로 구할 수 있을까요? 구현을 위해서는 우선 Lyndon Word와 Lyndon Decomposition에 대해 알아야 합니다.
Lyndon Word
자기 자신이 아닌 모든 suffix보다 사전순으로 작은 단어를 Lyndon Word라고 부릅니다.
Lyndon Word의 예시로는 $\rm{a, b, ab, aab, abac}$ 등이 있습니다.
Lyndon Word가 아닌 예시로는 $\rm{ba, abab}$ 등이 있습니다. 이는 직접 모든 suffix와 직접 비교해보면 쉽게 알 수 있습니다.
Lyndon Decomposition
어떤 문자열 $S$의 Lyndon decomposition은 $S=w_1 w_2 \cdots w_k$로 분할하는 것입니다. 이 때, 각 $w_i$는 Lyndon Word여야 하며, $w_1 \ge w_2 \ge \cdots \ge w_k$를 만족해야 합니다. $\ge$는 사전 순 비교를 의미합니다.
이 때, $w_1$은 Longest Lyndon Prefix, 즉 $S$의 prefix이면서 Lyndon word인 것들 중에서 가장 긴 문자열이 됩니다.
예를 들어, $\rm{banana}$의 Lyndon Decomposition은 $\rm{b \vert an \vert an \vert a}$이며, Longest Lyndon Prefix는 $\rm{b}$입니다.
이러한 Lyndon Decomposition은 항상 존재하며, 또한 유일하다고 알려져 있습니다.
Lyndon Decomposition 알고리즘
Lyndon Decomposition을 구하는 대표적인 알고리즘으로는 $O(n)$에 동작하는 Duval 알고리즘이 있습니다. 하지만, 새로운 알고리즘을 공부할 필요 없이 기존의 Suffix Array만을 활용해도 Lyndon Decomposition을 구할 수 있습니다.
Suffix Array를 구해 놓고, 그리디하게 기존 문자열에서 사전순으로 가장 작은 suffix부터 제거합니다. 이 때, 이미 제거된 suffix들은 무시합니다. 그러면, 제거되는 suffix의 목록이 Lyndon Decomposition을 구성합니다. 이렇게 해도 되는 이유는 koosaga님의 포스트를 참고하시기 바랍니다.
$\rm{banana}$의 경우를 예시로 들어봅시다. $\rm{banana}$의 suffix를 사전 순으로 모두 정렬하면 아래와 같습니다.
- $\rm{a}$
- $\rm{ana}$
- $\rm{anana}$
- $\rm{banana}$
- $\rm{na}$
- $\rm{nana}$
이때, suffix들을 사전 순서대로 보면서 순서대로 제거해봅시다. 이미 제거된 문자는 굵은 글씨로 표현하겠습니다.
- $\rm{a}$ → $\rm{a}$를 제거합니다.
- $\rm{an}\bf{a}$ → $\rm{an}$을 제거합니다.
- $\rm{an\bf{ana}}$ → $\rm{an}$을 제거합니다.
- $\rm{b\bf{anana}}$ → $\rm{b}$를 제거합니다.
- $\rm{\bf{na}}$ → 이미 제거되었으므로 넘어갑니다.
- $\rm{\bf{nana}}$ → 이미 제거되었으므로 넘어갑니다.
따라서, $\rm{banana}$의 Lyndon Decomposition인 $\rm{b \vert an \vert an \vert a}$를 올바르게 얻을 수 있습니다.
보시다시피 이 알고리즘은 구현이 전혀 어렵지 않으며, Suffix Array의 $O(n)$ 구현을 사용하는 경우 시간복잡도는 Duval 알고리즘과 마찬가지로 $O(n)$이 됩니다.
Run Enumerate 알고리즘
그래서 Lyndon Decomposition이 run을 구할 때 어떻게 활용되는 걸까요?
문자열 $S$가 주어질 때, 존재하는 모든 알파벳의 대소관계가 반대로 뒤집어지도록 변환한 문자열을 $-S$라고 합시다.
예를 들어 알파벳 소문자만 활용하는 경우, 모든 문자에 대해 s[i] = 'a' + 'z' - s[i]를 적용한다고 생각할 수 있습니다. 이 때 $\rm{a}$는 $\rm{z}$로, $\rm{b}$는 $\rm{y}$로, $\rm{c}$는 $\rm{x}$로, $\cdots$ 변환됩니다.
이제, $S$와 $-S$의 모든 suffix들에 대해 각각 Longest Lyndon Prefix를 구해봅시다.
$S$와 $-S$는 각각 $n$개의 suffix를 가지고, 각 suffix마다 하나의 Longest Lyndon Prefix를 가지므로 총 $2n$개의 문자열이 나오게 됩니다. 그러면, 이 $2n$개의 문자열들이 모두 문자열 $S$에서 반복되는 최소단위 문자열의 후보가 됩니다. (왜 그런지는 증명하지 않고 넘어가겠습니다.)
이렇듯 후보가 되는 문자열을 seed string이라고 부르겠습니다. 그러면, 이제 남은 것은 각 seed string이 얼마나 반복되는지 찾는 것입니다. 반복될 가능성이 있는 최소단위의 seed string을 찾았으니, 이제 그 seed string이 실제로 얼마나 반복되는지 찾을 차례입니다. seed string의 구간을 $[i, j)$로 두고 분석해봅시다.
예를 들어, 문자열 $S=\rm{cbacbababaa}$라고 합시다. $S$의 $5$번째 인덱스부터 시작하는 suffix는 $\rm{ababaa}$이며, $\rm{ababaa}$의 Longest Lyndon Prefix는 $\rm{ab}$입니다. 따라서 해당하는 구간 $[5, 7)$을 seed string으로 잡습니다.
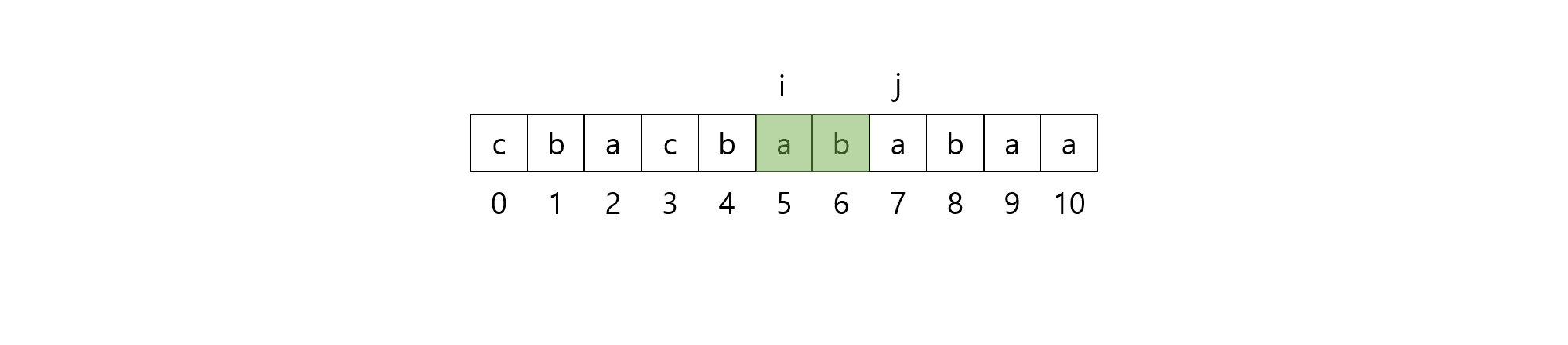
seed string이 반복되는 최소 단위임이 보장되므로, run에서의 $p$ 값을 $2$로 고정할 수 있습니다.
우리가 알고 싶은 것은 $[5, 7)$ 양 옆으로 seed string이 얼마나 반복되는지입니다. 즉, $(5-l, 7+k, 2)$가 run이 되도록 하는 가장 큰 $l\ge 0$과 $k\ge 0$를 구하고 싶습니다.
우선 오른쪽으로 얼마나 반복되는지 구해봅시다. 이는 모든 $0\le i < k$에 대해 $S[5+i] = S[7+i]$를 만족하도록 하는 가장 큰 $k$값이 무엇인지 구하는 것과 동일합니다.
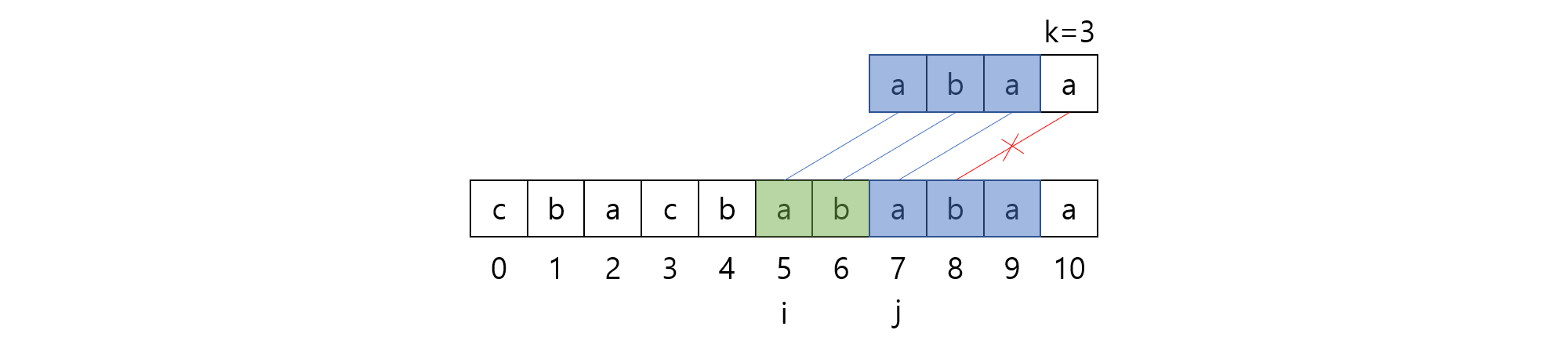
위 예시의 경우 $k$는 $3$이며, $k$값을 구하는 과정이 결국 $S[5..10]$과 $S[7..10]$의 Longest Common Prefix의 길이를 구하는 것과 동일하다는 것을 관찰할 수 있습니다!
마찬가지로, 왼쪽으로 얼마나 반복되는지 구하는 것은 모든 $0 \le i < l$에 대해 $S[4-i] = S[6-i]$를 만족하도록 하는 가장 큰 $l$값을 구하는 것과 동일합니다.
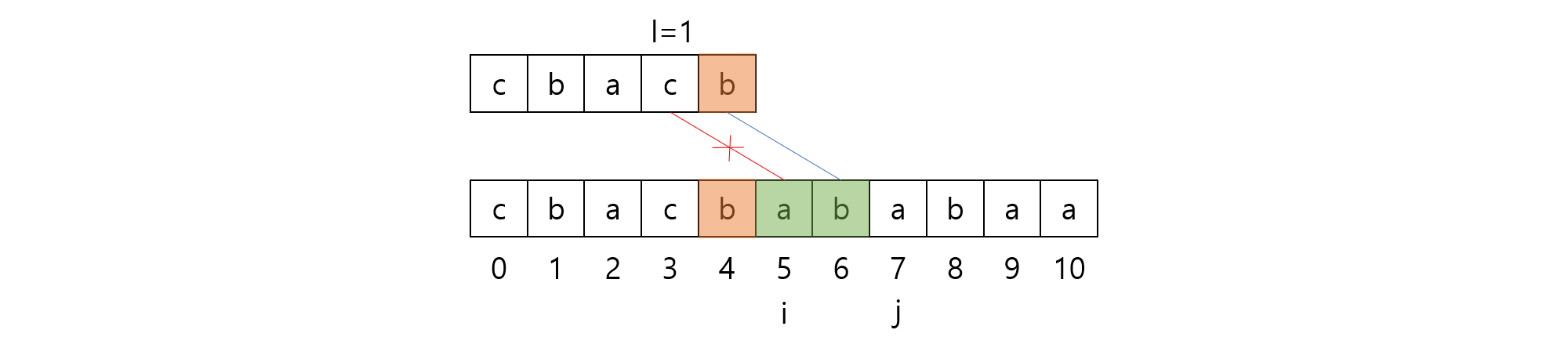
위 예시의 경우 $l$은 $1$이며, $l$값을 구하는 과정이 결국 $S[0..4]$과 $S[0..6]$의 Longest Common Suffix의 길이를 구하는 것과 동일하다는 것을 관찰할 수 있습니다!
위 예시에서는 $k=3$과 $l=1$을 얻었으므로, 최종적으로 산출되는 run은 $(5-l, 7+k, 2)=(4, 10, 2)$가 되며, $S=\rm{cbacbababaa}$에 존재하는 run 하나를 올바르게 찾았음을 알 수 있습니다.
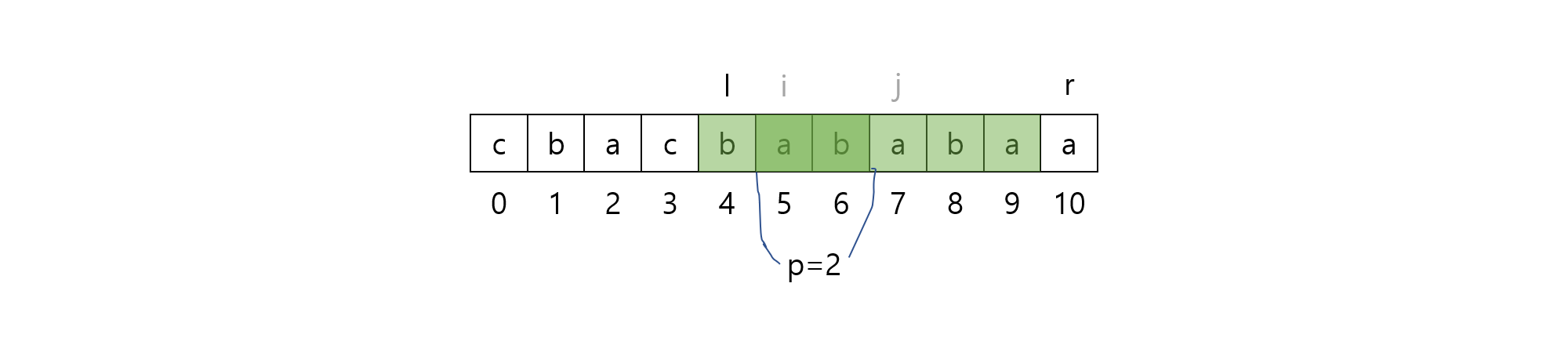
일반성을 잃지 않고, 모든 seed string $[i, j)$에 대해서 동일한 작업을 진행해줄 수 있습니다.
어떤 seed string의 구간 $[i, j)$가 주어지면, 이 seed string으로부터 비롯되는 run은 $(i-l, j+k, j-i)$입니다.
이 때, $k$의 값은 $S[i..n-1]$과 $S[j..n-1]$의 Longest Common Prefix의 길이이며, $l$의 값은 $S[0..i-1]$과 $S[0..j-1]$의 Longest Common Suffix의 길이입니다.
일반적으로, 인접한 두 suffix의 Longest Common Prefix의 길이를 나타내는 LCP 배열을 $O(n)$에 구하는 법이 잘 알려져 있으며, 임의의 두 suffix의 Longest Common Prefix는 LCP 배열에서 구간 최솟값 쿼리를 통해 $O(\log n)$에 알 수 있습니다.
Longest Common Suffix의 경우에는, 문자열을 뒤집어서 Longest Common Prefix 쿼리로 변환해줄 수 있습니다.
따라서, 하나의 seed string 후보에 대해 해당하는 run을 $O(\log n)$에 구할 수 있고, 총 $2n$개의 seed string 후보가 있으므로 총 시간 복잡도 $O(n \log n)$에 가능한 모든 run의 후보들을 구할 수 있습니다.
마지막으로, run에서 구간의 길이가 $p$의 2배 미만인 경우(즉, 정의상 run이 아닌 경우)와 중복된 run이 있는 경우를 모두 제거해주면 결과적으로 모든 run의 목록을 얻을 수 있습니다!
이 알고리즘이 존재하는 run을 모두 찾는다는 사실에 대한 증명 또한 아까 소개한 이 논문에서 찾을 수 있습니다.
Run Enumerate 구현
첫 번째로, $S$와 $-S$의 모든 suffix에 대해 Longest Lyndon Prefix를 구해야 합니다.
어떤 문자열의 모든 suffix에 대해 Longest Lyndon Prefix를 효율적으로 구하는 것은 위에서 설명한 Lyndon Decomposition을 응용하여 $O(n)$에 할 수 있습니다.
$i$번째 문자부터 시작하는 suffix $S[i..n-1]$를 $i$번 접미사라고 합시다.
$i+1$번, $i+2$번, $\cdots$, $n-1$번 접미사 중에서, $i$번 접미사보다 사전 순으로 앞선 접미사 중 가장 인덱스가 작은 것을 $j$번 접미사라고 합시다.
그러면, $i$번 접미사의 Longest Common Prefix는 $S[i..j-1]$이 됩니다. 이는 $i$번 접미사에 위에서 설명한 Suffix Array로 Lyndon Decomposition을 구하는 과정을 생각해보면 쉽게 알 수 있습니다.
$j$번 접미사의 의미는, $i$번 접미사가 제거되기 전에 제거된 접미사들 중 가장 왼쪽에 있는 것입니다. 따라서, Lyndon Decomposition을 구하는 과정 중 $i$번 접미사가 제거될 때에 실제로 제거되는 문자열은 $S[i..j-1]$이며, 이것이 $i$번 접미사의 Lyndon Decomposition의 가장 첫 단어가 됩니다. 따라서 $S[i..j-1]$이 $i$번 접미사의 Longest Lyndon Prefix가 됨을 알 수 있습니다.
이제 남은 것은 모든 $i$에 대해 $i$번째 접미사보다 사전 순으로 앞서면서 인덱스가 가장 작은 접미사 번호 $j$를 관리하는 것입니다.
이는 길이가 가장 짧은 접미사부터, 즉 $n-1$번 접미사부터 $n-2$번 접미사, $n-3$번 접미사, $\cdots$를 순서대로 보면서 monotone stack에 자신보다 사전 순으로 작은 접미사 번호만 들어 있도록 관리해주면 $O(n)$에 전부 구할 수 있습니다. 상세한 구현은 아래 코드의 use_lyndon() 함수를 참고해주세요.
위 방식대로 seed string들을 구하면, 남은 작업은 임의의 두 접미사가 주어지면 두 접미사의 Longest Common Prefix를 구하는 것입니다. 이는 구간 최솟값 쿼리를 통해 $O(\log n)$에 가능하며, 아래 코드에서는 sparse table을 이용해 구간 최솟값 쿼리를 구현하였습니다.
Longest Lyndon Prefix와 sparse table을 포함하여, 필요한 모든 알고리즘을 통합한 코드는 아래와 같습니다. C++17 기준으로 yosupo의 Run Enumerate Library Checker를 통과하도록 짜여졌습니다.
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct String {
vector<int> sa, r, nr, lcp, lyndon;
vector<vector<int>> mn;
vector<tuple<int,int,int>> runs;
string s;
int lg, n;
String(string& s):s(s), n(s.size()) {}
bool cmp(int i, int j, int d) {
if(r[i] == r[j]) return r[i+d] < r[j+d];
return r[i] < r[j];
}
void use_sa() {
if(!sa.empty()) return;
int m = max(256, n) + 1;
sa = vector<int>(n); r = nr = vector<int>(n+n);
vector<int> t[m];
for(int i=0;i<n;i++) sa[i] = i, r[i] = s[i];
for(int d=1;r[sa[n-1]]!=n;d<<=1) {
for(int j=d;j>=0;j-=d) {
for(int i=0;i<m;i++) t[i] = vector<int>();
for(int i:sa) t[r[i+j]].push_back(i); sa.clear();
for(int i=0;i<m;i++) for(int x:t[i]) sa.push_back(x);
}
nr[sa[0]] = 1;
for(int i=1;i<n;i++) nr[sa[i]] = nr[sa[i-1]] + cmp(sa[i-1], sa[i], d);
swap(r, nr);
}
for(int i=0;i<=n;i++) r[i]--;
}
void use_lcp() {
if(!lcp.empty()) return;
use_sa();
lcp = vector<int>(n);
int l = 0;
for(int i=0;i<n;i++) {
if(r[i]) {
int j = sa[r[i]-1];
while(s[i+l] == s[j+l]) l++;
lcp[r[i]] = l;
}
if(l) l--;
}
}
void use_query() {
if(!mn.empty()) return;
use_lcp();
lg = 0;
while(n >= (1 << lg)) lg++;
mn = vector<vector<int>>(lg, vector<int>(n+n));
for(int i=0;i<n;i++) mn[0][i] = lcp[i];
for(int j=1;j<lg;j++) for(int i=0;i<n;i++) mn[j][i] = min(mn[j-1][i], mn[j-1][i + (1<<j-1)]);
}
int query(int a, int b) {
use_query();
if(a < 0 || b < 0 || a >= n || b >= n) return 0;
if(a == b) return n - a;
a = r[a], b = r[b];
if(a>b) swap(a,b);
a++;
int l = b - a + 1;
int ret = 1e9;
for(int i=lg-1;i>=0;i--) if(l&(1<<i)) ret = min(ret, mn[i][a]), a += (1<<i);
return ret;
}
void use_lyndon() {
if(!lyndon.empty()) return;
use_sa();
lyndon = vector<int>(n);
vector<int> t;
t.push_back(n);
for(int i=n-1;i>=0;i--) {
while(!t.empty() && r[t.back()] > r[i]) t.pop_back();
lyndon[i] = t.back();
t.push_back(i);
}
}
void use_runs() {
if(!runs.empty()) return;
string t = s;
reverse(t.begin(), t.end());
String rs(t);
t = s;
for(char& c:t) c = 'a' + 'z' - c;
String is(t);
use_query();
use_lyndon();
rs.use_query();
is.use_lyndon();
for(int i=0;i<n;i++) {
ll j = lyndon[i];
ll l = i - rs.query(n-i, n-j);
ll r = j + query(i, j);
ll p = j - i;
if(r - l >= 2 * p) runs.push_back({p, l, r});
}
for(int i=0;i<n;i++) {
ll j = is.lyndon[i];
ll l = i - rs.query(n-i, n-j);
ll r = j + query(i, j);
ll p = j - i;
if(r - l >= 2 * p) runs.push_back({p, l, r});
}
sort(runs.begin(), runs.end());
runs.erase(unique(runs.begin(), runs.end()), runs.end());
}
};
string _s;
int main() {
// ios_base::sync_with_stdio(0); cin.tie(0);
cin >> _s;
String s(_s);
s.use_runs();
cout << s.runs.size() << "\n";
for(auto [p,l,r]:s.runs) cout << p << " " << l << " "<< r << "\n";
}
String 구조체는 String(s)와 같이 문자열을 넘겨줌으로써 생성할 수 있으며, 초기화 시 넘겨진 문자열 s에 대해 Suffix Array, LCP, Run Enumerate 등의 작업을 진행할 수 있는 함수를 제공합니다.
use_sa() 함수는 처음 호출되는 경우 구조체 멤버 벡터 sa에 사전순으로 정렬된 접미사 번호를 순서대로 저장하고, 구조체 멤버 벡터 r에 각 접미사의 사전순 rank를 저장합니다. 기본적으로 일반적인 Suffix Array와 동일하게 동작합니다.
위 코드에서는 Suffix Array가 $O(n \log n)$으로 비효율적으로 구현되어 있어, 많은 경우에 시간 초과를 받을 가능성이 높으므로 Atcoder Library 등에서 $O(n)$으로 구현된 것을 찾아서 쓰는 것을 강력히 추천드립니다.
use_lcp() 함수는 처음 호출되는 경우 구조체 멤버 벡터 lcp에 LCP 배열을 저장합니다.
use_query() 함수는 처음 호출되는 경우 LCP 배열의 구간 최솟값 쿼리에 쓰이는 sparse table을 초기화합니다.
query(int a, int b) 함수는 접미사 번호 $a$와 $b$를 넘겨주면 sparse table을 이용해 해당하는 두 접미사의 Longest Common Prefix의 길이를 반환해줍니다.
use_lyndon() 함수는 처음 호출되는 경우 구조체 멤버 벡터 lyndon에 각 접미사별로 Longest Lyndon Prefix의 끝 위치를 저장합니다.
use_runs() 함수는 처음 호출되는 경우 구조체 멤버 벡터 run에 존재하는 모든 run의 tuple을 저장합니다. $S$를 $-S$로 변환할 때 for(char& c:t) c = 'a' + 'z' - c;를 사용하며, 이는 문제에서 요구하는 알파벳의 범위에 따라 수정해서 사용하셔야 합니다.
[연습 문제] Tandem Repeats (BOJ 9483)
동일한 문자열 $T$가 두번 반복되는 $TT$ 형태의 문자열을 Tandem Repeat이라 할 때, 문자열에 존재하는 모든 Tandem Repeat을 (중복을 포함하여) 세는 문제입니다.
우선 우리가 모든 run의 목록을 가지고 있다고 생각해봅시다.
하나의 run $(l,r,p)$가 있을 때, 이 run 안에 존재하는 Tandem Repeat은 다음과 같습니다.
- 길이 $2p$인 Tandem Repeat : $r-l-2p+1$개
- 길이 $4p$인 Tandem Repeat : $r-l-4p+1$개
- 길이 $6p$인 Tandem Repeat : $r-l-6p+1$개
- $\cdots$
이는 등차수열의 합 형태이므로 $r-l-2kp+1 > 0$인 가장 큰 $k$를 구해서 합을 $O(1)$에 계산해줄 수 있습니다. 이때, 한 문자열에 존재하는 run의 개수는 최대 $n$개이므로, 모든 run에 대해서 등차수열의 합을 구해주면 $O(n)$에 정답을 얻을 수 있습니다.
하지만, 이는 결국 가능한 모든 $p$의 배수에 대해 보는 것이므로 위에서 본 run의 2번째 성질에 따라 그냥 단순히 합을 구해도 시간복잡도는 $O(n)$으로 차이가 없습니다. 따라서, 아래의 코드처럼 간단하게 답을 구해줄 수 있습니다.
Run Enumerate의 시간 복잡도가 $O(n \log n)$이므로, 최종 시간복잡도는 $O(n \log n)$입니다.
ll ans = 0;
for(auto [p, l, r]:s.runs) {
int len = r - l;
for(int i=1;p*i<=len;i++) {
ans += max(0, len - 2 * p * i + 1);
}
}
[연습 문제] Repeats (BOJ 22218)
문자열 $T$가 $k$번 연속해서 나타나는 문자열을 $T^k$라 할 때, 문자열 $S$가 주어지면 $T^k$ 형태의 모든 부분 문자열들 중 $k$가 가장 큰 것을 찾는 문제입니다. 즉, 가장 많이 반복되는 부분 문자열을 찾는 문제입니다.
출력해야 하는 것은 아래와 같습니다.
- 그 때의 반복 횟수
- 반복되는 문자열의 길이
- 해당 부분문자열이 시작하는 위치
우선 하나의 run $(l,r,p)$에 대해 생각해봅시다.
이 run이 포함하는 반복 중 반복 횟수를 제일 크게 할 수 있는 것은 길이 $p$의 문자열을 반복할 때이며, 이 때의 반복 횟수 $k$는 $\lfloor (r-l)/p \rfloor$입니다.
따라서 모든 run에 대해 $\lfloor (r-l)/p \rfloor$의 최댓값을 구하고, 그 때 반복되는 문자열의 길이인 $p$와 시작 위치 $l$도 같이 관리해주면 문제를 풀 수 있습니다. 하나의 run을 처리하는데 $O(1)$이 걸리고, 최대 $n$개의 run이 있으므로 시간복잡도는 $O(n)$입니다.
Run Enumerate의 시간 복잡도가 $O(n \log n)$이므로, 최종 시간복잡도는 $O(n \log n)$입니다.
for(auto [p, l, r]:s.runs) {
int k = (r - l) / p;
if(mx < k) {
mx = k;
len = p;
idx = l + 1;
}
}
[연습 문제] Good Partitions (BOJ 25740)
문자열의 부분문자열들 중 $AABB$형태가 되는 것이 몇 개인지 (중복을 포함하여) 세는 문제입니다. 이 때 문자열 $A$, $B$는 비어있지 않아야 하며, $A$와 $B$가 같을 수도 있습니다.
이때, $AA$와 $BB$가 의미하는 것은 위에서 본 Tandem Repeat과 동일한 개념입니다. 따라서, 이 문제는 서로 붙어서 나오는 Tandem Repeat이 총 몇 개인지 세는 문제로 볼 수 있습니다.
이를 효율적으로 세기 위해서는, 각 문자마다 그 문자에서 시작되는 Tandem Repeat의 개수와 그 문자에서 끝나는 Tandem Repeat의 개수를 저장해주면 됩니다.
$i$번째 문자에서 시작하는 Tandem Repeat의 개수를 $s[i]$, $i$번째 문자에서 끝나는 Tandem Repeat의 개수를 $e[i]$라고 합시다. 그러면 정답을 $\sum_{i=1}^{\vert S \vert -1} e[i-1] \cdot s[i]$처럼 나타낼 수 있습니다.
이제 남은 것은 $s[i]$와 $e[i]$를 올바르게 관리하는 것입니다.
하나의 run $(l,r,p)$가 있을 때, 이 run 안에 존재하는 Tandem Repeat은 다음과 같습니다.
- 길이 $2p$인 Tandem Repeat : $r-l-2p+1$개
- 길이 $4p$인 Tandem Repeat : $r-l-4p+1$개
- 길이 $6p$인 Tandem Repeat : $r-l-6p+1$개
- $\cdots$
이 때, 길이 $2p$인 Tandem Repeat은 $r-l-2p+1$개이고, 각각의 시작 위치는 $l, l+1,\cdots, r-2p$입니다. 따라서, $l\le i \le r-2p$를 만족하는 모든 $s[i]$에 1을 더해주면 됩니다. 마찬가지로, 각각의 끝 위치는 $l+2p-1, l+2p, \cdots, r-1$이므로 $l+2p-1\le i \le r-1$를 만족하는 모든 $e[i]$에 1을 더해주면 됩니다.
이는 구간 업데이트이므로, Fenwick Tree나 Segment Tree with Lazy Propagation을 이용하면 $O(\log n)$에 업데이트해줄 수 있습니다.
길이 $4p$인 Tandem Repeat의 경우도 동일하게 $l\le i \le r-4p$를 만족하는 모든 $s[i]$에 1을 더해주고, $l+4p-1\le i \le r-1$를 만족하는 $e[i]$에 1을 더해주면 됩니다.
길이 $6p$인 Tandem Repeat의 경우도 동일하게 $l\le i \le r-6p$를 만족하는 모든 $s[i]$에 1을 더해주고, $l+6p-1\le i \le r-1$를 만족하는 $e[i]$에 1을 더해주면 됩니다.
같은 작업을 모든 run에 대해 반복해주면 $s[i]$와 $e[i]$를 모두 올바르게 구할 수 있습니다. run의 성질에 따라 가능한 모든 반복을 보는 것은 $O(n)$이며, 각 반복마다 $O(\log n)$의 구간 업데이트가 있으므로 총 시간복잡도는 $O(n \log n)$입니다.
마지막으로 $\sum_{i=1}^{\vert S \vert -1} e[i-1] \cdot s[i]$을 구해 출력하면 정답을 받을 수 있습니다. Fenwick Tree나 Segment Tree with Lazy Propagation을 사용하는 경우, 이 과정의 시간 복잡도는 $O(n \log n)$입니다.
Run Enumerate의 시간 복잡도도 $O(n \log n)$이므로, 최종 시간복잡도는 $O(n \log n)$입니다.
[연습 문제] Repetitions (BOJ 25111)
문자열 $S$가 주어지고, 쿼리 $(a, b)$가 주어질 때 마다 $S$의 부분 문자열 $S[a..b]$에 나타나는 $TT$ 형태의 부분 문자열 중 가장 긴 것을 찾고, 가장 긴 것이 여러 개라면 가장 왼쪽에 등장하는 것을 찾는 문제입니다.
출력해야 하는 것은 아래와 같습니다.
- 가장 긴 $TT$ 형태의 부분 문자열이 있을 때, $T$의 길이
- 가장 긴 $TT$ 형태의 부분 문자열이 등장하는 가장 처음 위치, 가장 긴 것이 여러개라면 가장 왼쪽에 있는 것
우선 문제는, Run Enumerate를 쿼리로 들어오는 모든 부분 문자열에 대해서 해줘야 한다는 것입니다. 하지만 꼭 그럴 필요는 없다는 것을 관찰할 수 있습니다.
Run Enumerate를 전체 문자열 $S$에 대해 해놓으면, 그 결과를 $S$의 부분 문자열에 대해서도 재사용할 수 있기 때문입니다.
부분 문자열 $S[a..b]$에 대해서, 모든 run $(l, r, p)$에 대해 $l’ = max(l, a)$, $r’ = min(r, b)$를 적용해준 뒤 $(l’,r’,p)$들 중 run의 조건을 만족하지 않는 것들을 제거해주면 부분 문자열 $S[a..b]$에 대한 모든 run의 목록을 얻을 수 있습니다. 즉, $S$에서 양 옆을 잘라 $S[a..b]$가 된 것처럼 run의 구간도 필요한 경우 양 옆을 잘라주는 것이죠.
이 때, 주어지는 쿼리의 개수 $q$가 100 이하이기 때문에, 쿼리가 들어올 때 마다 $n$개의 run들을 일일이 잘라서 새로운 run들의 목록을 만들어도 $O(nq)$로 시간 복잡도의 여유가 있게 됩니다.
쿼리로 들어온 부분 문자열 하나에서 가장 긴 $TT$ 형태의 문자열을 찾는 것은 아래와 같이 해줄 수 있습니다.
부분 문자열에 대한 하나의 run $(l’, r’, p)$에 대해서, 이 run에서 등장하는 가장 긴 $TT$ 형태의 문자열의 길이는 $\lfloor r’-l’/2p \rfloor \cdot 2p$입니다. 따라서 이 때의 $T$의 길이는 $\lfloor r’-l’/2p \rfloor \cdot p$이며, 등장하는 가장 왼쪽 위치는 $l’$입니다. 따라서, 모든 $run$에 대해 $\lfloor r’-l’/2p \rfloor \cdot p$의 최댓값을 구하고, 최댓값과 함께 $l’$ 값도 함께 관리하면 문제를 풀 수 있습니다.
한 쿼리당 $O(n)$의 시간이 걸리므로, 쿼리를 전부 처리하는데 걸리는 시간은 $O(nq)$이며 Run Enumerate의 시간 복잡도가 $O(n \log n)$이므로, 최종 시간 복잡도는 $O(n \log n + nq)$입니다.
[연습 문제] Square Substrings (BOJ 18658)
동일한 문자열 $T$가 두번 반복되는 $TT$ 형태의 문자열을 square라고 합시다.
문자열 $S$가 주어지면, 각 쿼리 $(l,r)$에 대해 $S$의 부분 문자열 $S[l..r]$에 포함된 square의 개수가 몇 개인지 세는 문제입니다.
square가 의미하는 것은 위의 Tandem Repeat과 동일한 개념이며, Tandem Repeat 문제의 쿼리 버전이라고 볼 수 있습니다.
문자열의 길이 $n$과 쿼리의 개수 $q$ 모두 $1\le n, q\le 10^6$을 만족하기 때문에, Repetitions에서 했던 것처럼 부분 문자열 쿼리가 들어올 때 마다 $n$개의 run을 전부 잘라주는 방법은 불가능합니다.
하지만, 굳이 $n$개의 run을 전부 잘라야 할까요?
쿼리 $(l,r)$이 주어졌을 때, 이 부분 문자열에서 square의 개수를 세는 데 필요한 run들은 아래와 같이 두 가지로 분류할 수 있습니다.
- run의 구간이 구간 $[l,r]$에 완전히 포함됨
- run의 구간이 $l-1$을 포함하거나 $r+1$을 포함함
이 두 가지는 서로 disjoint하며, 부분 문자열 $S[l..r]$의 run을 구하는데 필요한 모든 run을 포함합니다. 따라서, 두 경우로 나누어 구해주어도 $S[l..r]$에 포함된 run을 전부 구할 수 있습니다.
run의 구간이 구간 $[l,r]$에 완전히 포함되는 경우, 구간에 완전히 포함되는 run은 $l, r$을 조정해줄 필요 없이, 즉 자를 필요 없이 그대로 활용할 수 있습니다. 따라서, 세그먼트 트리 등을 이용해서 특정 구간에 완전히 속하는 run의 square의 개수를 모두 합할 수 있도록 전처리해주면 $[l, r]$ 구간에 완전히 속하는 square의 개수를 $O(\log n)$에 구할 수 있습니다.
$l-1$ 또는 $r+1$을 포함하는 run들은 양 끝값에 대한 조정이 필요합니다. 즉, $S[l..r]$과 일부만 겹치기 때문에 run들을 잘라줘야 하며, 전처리해둔 값을 그대로 활용할 수 없습니다. 따라서 어쩔 수 없이 일일이 자른 후에 square의 개수를 구해줘야 합니다.
그런데 한 점에서 겹치는 run에 개수는 매우 적다는 사실을 이용하면, $l-1$ 또는 $r+1$에 겹치는 run들을 모두 일일이 보아도 시간복잡도의 손해를 보지 않습니다. 위에서 언급했듯이, 일일이 보더라도 $O(\log n)$의 시간이 걸리는 것으로 추정됩니다. 추정일 뿐이지만, 편의상 한 점에 겹치는 run의 개수를 $O(\log n)$이라고 두도록 하겠습니다.
또한 한 점에 겹치는 run들은 미리 전처리해둘 수 있습니다. 한 점에서 겹치는 run의 개수가 $O(\log n)$이기 때문에, 모든 점에 대해서 겹치는 run들을 미리 구해놓더라도 공간복잡도는 $O(n \log n)$이 되어 충분합니다.
따라서, 위 방법을 이용하면 쿼리 당 $O(\log n)$에 부분 문자열 $S[l..r]$에 대한 square의 개수를 모두 구할 수 있으며, 쿼리를 전부 처리하는데 드는 시간복잡도는 $O(q \log n)$입니다. Run Enumerate의 시간 복잡도가 $O(n \log n)$이므로, 최종 시간 복잡도는 $O(n \log n + q \log n)$가 되어 문제를 풀 수 있습니다.