Concurrent Augmented Tree
Intro
이전의 글에서 Concurrent Non-Blocking Binary Search Tree를 알아보았다. 이번에는 단순히 Insert, Delete, Find만 지원하는 트리가 아니라, Range Query를 지원하는 자료구조에 대해서 알아보자.
Key Points & Brainstorming
이전의 글에서 알아봤던 lock-free-locks로 만든 leaf tree, 그리고 Ellen Tree는 모두 Insert, Delete, 그리고 Find (혹은 Lookup) 연산만을 지원한다. 아주 중요한 연산들이지만, 실제로 자료구조를 사용할 때는 더 다양한 종류의 연산들이 필요한 경우가 많다.
흔히 Seqential한 환경에서 생각해볼 수 있는 연산은, Range sum 연산이다. key_l과 key_r이 주어졌을 때, 트리 내에 있는 데이터들 중 key값이 해당 구간 안에 있는 데이터들의 합을 구하는 연산이다. 굳이 sum이 아니더라도 max, min, gcd, xor 등 다양한 연산들에 대해서 생각해볼 수도 있다. 이러한 데이터를 augmented data, 이런 데이터와 연산을 지원하는 트리를 augmented tree라고 부르자.
이 연산을 concurrent BST에 적용하려면 (lock을 사용하더라도) 굉장히 골치아픈데, 이 range query는 필연적으로 많은 수의 노드를 ‘동시에’ 접근해야 하기 때문이다. 여기서 ‘동시’의 의미는 atomicity로, 해당 연산을 처리하기 위해 동일한 snapshot에 속하는 노드들을 봐야 한다는 뜻이다. 어떠한 연산이든 linearizable해야 하고 sequential한 세팅에서 나올 수 있는 값을 반환해야 하는데, 서로 다른 노드를 따로 읽게 되면 그 사이에 다른 스레드가 데이터를 변경할 수 있어, sequential한 환경에서 (또는, linearization point 상에서) 동시에 존재할 수 없었던 정보를 읽고 반환할 수 있기 때문이다.
기존의 Concurrent BST에서 지원하는 insert 혹은 find 연산의 경우에는 해당 key가 위치한 장소까지 이동한 후, 그 주변의 1-3개 노드만 ‘동시에’ 접근하면 되었다. 하지만 range query의 경우 O(h)개의 노드의 정보를 모두 수합해서 반환해야 한다. 동시에 다른 연산들을 처리하고 있는 다른 스레드들도 마찬가지이고, 그렇다면 서로의 연산에 영향을 주거나 서로를 기다려야 한다. 이 상황을 어떻게 해소할 수 있을까?
가장 먼저 생각할 수 있는 방법은 매 업데이트 (삽입, 삭제) 마다 해당 리프로부터 루트까지의 경로에 있는 모든 노드들의 새로운 복사본을 만들고, 기존의 노드들로 포인터를 연결하고, 거기서 업데이트한 후에, CAS 연산으로 루트를 바꾸기를 시도하고, 실패하면 처음부터 다시 시도하는 것이다. 이러한 Persistent Tree 방식은 range / find query에서는 다른 스레드들과 간섭하지 않아 O(h)이지만, update에서는 모든 스레드들이 루트에서 부딪히기 때문에 O(C h)이다. 여기서 C는 평균적으로 ‘contending’ (부딪히는 / 경쟁하는) 스레드들의 개수이다.
현재 시도된 방법은 크게 두가지이다. 간략하게 설명하자면, 하나는 각 노드가 자신의 버전 역사를 모두 가지고 있으며 쿼리가 들어올 때마다 해당 버전들을 뒤져보는 것, 다른 하나는 원래 트리 이외에 또다른 persistent한 트리를 따로 관리하면서 쿼리는 그 persistent (immutable) 한 트리에서 정보를 읽는 것이다. 전자는 Gal Sela의 논문 https://arxiv.org/pdf/2405.07434v1, 후자는 Panagiota Fatourou의 논문이다. https://arxiv.org/pdf/2405.10506. 두 논문 모두 무척 최근의 논문이고, (2025 DiSC) 둘 다 흥미로운 아이디어들이 있지만, 이 글에서는 더 나은 시간 복잡도를 주는 후자의 논문을 보도록 하자.
Fatourou, Ruppert Augmented Tree
이 논문에서 가장 중요한 아이디어는 트리의 구조를 관리하는 Node tree와, augmented data를 담당하는 Version tree로 나누어, Version tree를 persistent하게 관리한다는 점이다. 위의 Persistent Tree의 접근 방식과의 차이점은, 경로를 전부 한꺼번에 CAS하는 대신, 경로상의 노드 하나씩 CAS해서 실패 빈도를 낮추고 contention을 줄인다는 점이다.
이 논문에서 제안하는 augmentation은 다양한 종류의 트리에 적용할 수 있다. external tree (데이터가 리프 노드에만 있는 경우), 그리고 rotation이 없는 unbalanced tree의 경우에 insert, delete, find가 지원되는 트리라면 lock 없이 일반적으로 적용할 수 있는 방법론을 제안한다. 우리는 저번 포스팅에서 알아봤던 lock-free-locks를 이용한 단순한 Leaf Tree에 대해서 생각해보자.
먼저, 기본적인 데이터 구조부터 확인하자.
Node는 기존 underlying 트리 구조에서 사용하는 노드 데이터이고, 추가적으로 현재의 version 포인터를 담고 있다. 이외의 필드들은 기존의 트리와 동일하다. 예를 들어, Info 포인터도 Ellen Tree에서 노드 추가, 삭제를 위해 사용하는 필드이다.
추가적으로 Version 데이터 타입을 정의하는데, 이 데이터가 persistent tree를 이룰 데이터 노드이다. 한번 생성되어 트리에 추가되고 나면 절대 key, left, right, sum 값이 변하지 않을 것이다.
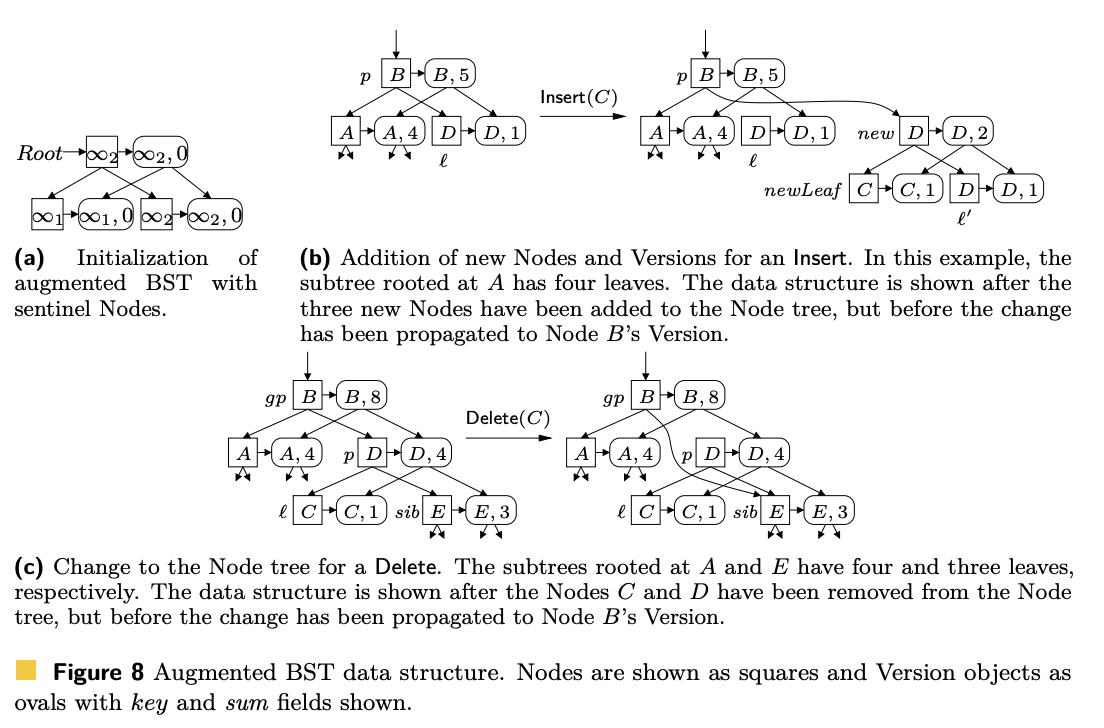앞서 언급한 대로, 이 구조에서는 기본적으로 트리의 두 가지 레이어가 있다고 보면 된다. 트리의 구조와 업데이트에 관여하는 Node tree, 그리고 데이터를 읽는데 관여하는 Version tree이다. 모든 read query들은 root에서 Version tree로 들어가고, Node tree에 접근하지 않는다. 모든 update query는 Node tree와 Version tree를 모두 업데이트하며, Version tree가 Node tree의 상태와 매칭되도록 관리한다.
위의 그림처럼, 각 version 노드들은 immutable하기 때문에, persistent tree를 관리해주는 것 처럼 각 노드의 복사본으로 포인터를 옮겨주게 된다.
기존의 트리에서 (논문에서는 Ellen tree) update query들이 가지는 차이점이 shaded로 표시되어 있다. 차이점 자체는 비교적 단순한데, insert할 때 새로운 version 노드를 만들어서 새로 생성된 노드가 참조하도록 한다는 점과, 결과를 반환하기 직전에 항상 Propagate(stack)을 부른다는 점이다.
여기서 stack은 현재 업데이트하고 있는 곳을 찾아온 경로로, search path라고도 부른다. propagate 함수는 해당 경로상에 있는 모든 노드들에 대해, 아래서부터 하나씩 version 포인터들을 업데이트하는 함수이다. 즉, Node tree와 Version tree의 정합성을 맞춰주는 함수라고 생각할 수 있다. 함수가 실패하더라도 반환 이전에 항상 propagate를 해주는 이유는, 다른 read query들과의 linearization을 맞춰주기 위해서이다. update query들은 Node tree를 접근하는데, 만약 현재의 Version tree가 내가 실패한 상태를 담고 있지 않다면 동시에 일어나는 read query들과 linearization이 불가능할 수 있다. 따라서 항상 반환하기 전에는 propagate을 불러 linearization이 가능하도록 보장한다.
Refresh 함수와 Propagate 함수가 앞서 언급한 Node tree와 Version tree의 정합성을 맞춰주는 함수이다. 아래의 Find, Select, Size 함수들은 다양한 read query들의 예시로서, Version tree를 따라 읽으면 linearizable하게 다양한 연산들을 지원할 수 있다는 예시들로 이해할 수 있다.
refresh 함수는 한 노드에 대해, 그 노드의 version 노드를 최신 정보로 업데이트해주는 내용이다. children의 정보를 읽기 전에 자신의 version 포인터를 읽어들인다는 점에 유의하자. version 포인터를 읽은 시점의 snapshot을 읽기를 기대하고 이후에 children 정보를 읽고, 마지막에 CAS를 함으로써 ‘내가 봤던 시점의 정보가 맞다면 이것으로 업데이트하라’ 는 연산을 수행할 수 있다.
propagate 함수는 단순히 스택의 가장 위 (가장 리프와 가까운 노드) 부터 refresh해주는 내용이다. 여기서 중요한 점은 만약 refresh 함수 (의 CAS 연산이) 실패할 경우, 한 번 더 실행해줘야 한다는 점이다. 내가 성공할 때 까지가 아니라 한 번만 재시도하면 되는 이유는, 내가 실패한 경우에 다른 스레드가 내가 업데이트해야 하는 정보를 대신 업데이트해주었을 것이기 때문이다. 첫 번째 실패한 경우에는 다른 스레드가 자식 정보를 읽어들인 이후에 내가 업데이트 했을 수 있기 때문에 재시도해야 하지만, 두번째 시도가 실패한 경우에는 내 정보를 다른 스레드가 읽었을 것이 확실하고, 그 CAS 연산이 나보다 먼저 시행되었음이 확실하기 때문에, 굳이 내가 업데이트를 하지 않아도 된다.
Closing
해당 자료구조는 캐시를 무시할 경우 O(h) 시간 안에 insert, delete, find, range sum 등의 연산들을 처리할 수 있다. 앞서 언급되었던 Gal Sela와 Erez Petrank의 다른 논문에서는 update 혹은 range query 둘 중 하나는 O(C h) 시간이 걸리는데, 이에 비교하면 더 나은 결과라고 볼 수 있다.
주의할 점은 Version tree와 Node tree의 모습이 완전히 일치하지는 않을 수 있다는 점이다. update query들은 과거 상태의 search path를 사용하기 때문에, 처리 중간에 다른 연산들이 트리의 모습을 바꾸게 된다면 내가 이미 삭제된 노드의 version 노드를 업데이트하거나 집어넣을 수 있다. 하지만 트리의 topology가 다르다고 하더라도 refresh 함수 내에서 보았든 Node tree와 Version tree의 (주어진 query 상에서의) 정합성은 보장되기 때문에 query들의 반환 결과들은 linearizable할 것이다.
구현체는 https://github.com/Diuven/pillar/blob/main/structures/ericTree.hpp 에 공개될 예정이다.
다음 포스팅에서는 이 트리의 correctness의 증명, 실제 구현상의 고려점, 또는 rotation의 지원 등에 대해서 짚어보도록 하자.