TAMREF's profile image

TAMREF

July 28, 2024 00:00

Introduction : Erdős–Pósa Theorem

Feedback Vertex Set (FVS) 이란, 그래프에서 $m$ 개 이하의 정점을 제거하여 forest로 만들 수 있는지를 묻는 문제입니다. 보다 엄밀하게, $G[V - X]$ 에 사이클이 존재하지 않는 $\lvert X \rvert \le m$ 이 존재하는지를 판별하는 문제입니다. 가령 아래 그래프에는 크기 2의 feedback vertex set $\lbrace B, D\rbrace$가 존재합니다.

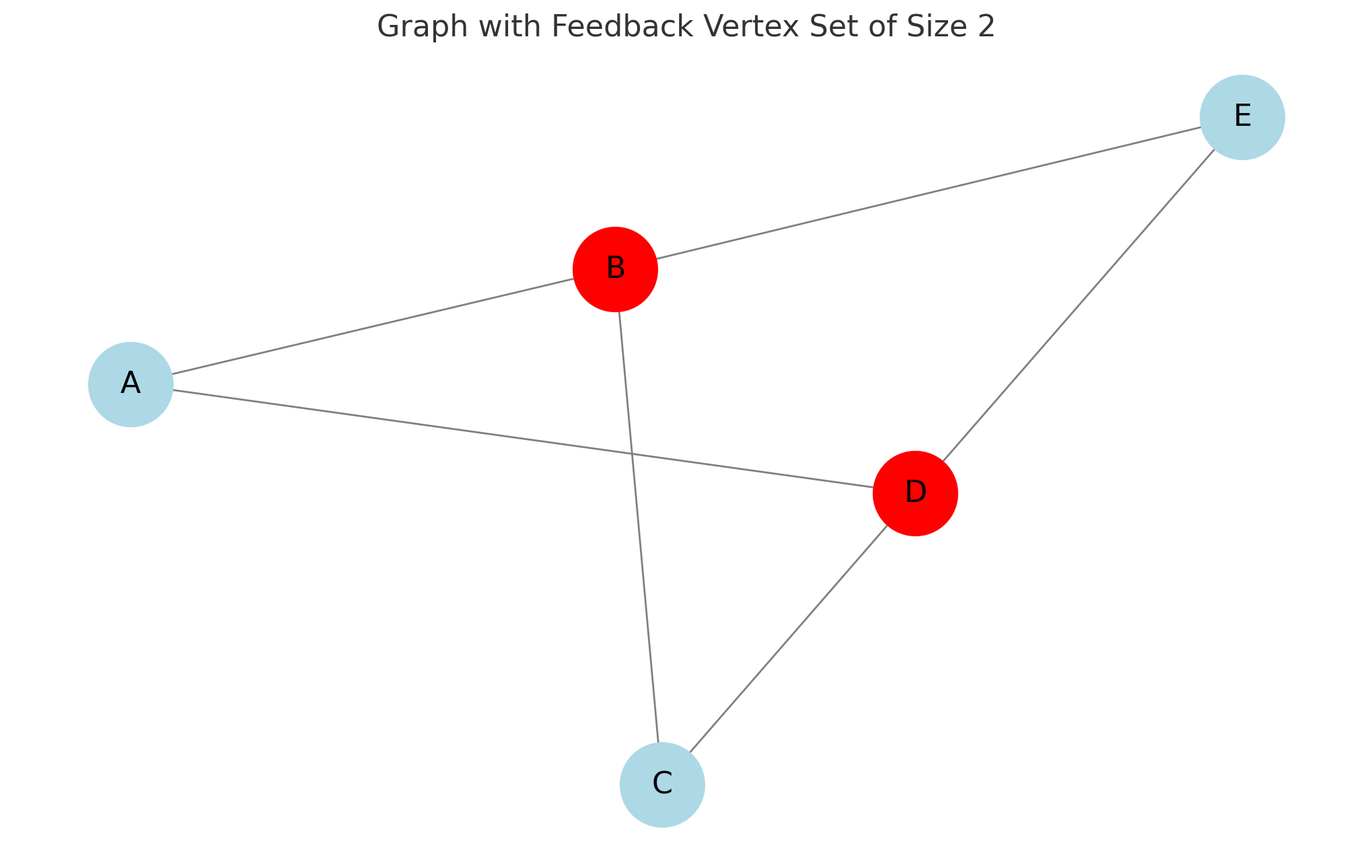
일반적으로 FVS는 NP-complete 문제임이 알려져 있지만, 제거할 정점의 개수 $m$ 이 상수라고 가정하면 그래프의 크기에 대해서는 다항 시간에 해결할 수 있습니다. 예를 들어 $O(8^{m} \cdot n^{2})$ 의 간단한 알고리즘이 알려져 있습니다 (Cao, 2017).

반대로, Feedback vertex set을 풀 수 없다는 사실은 어떻게 알 수 있을까요? 가장 단순하게, 모든 cycle들이 vertex disjoint한 경우에는 최소한 서로 다른 cycle 개수만큼을 제거해야 할 것입니다. 그리고 정확히 cycle 당 하나씩 정점을 골라서 제거할 수 있을 테니, 이 경우에는 FVS의 크기에 대한 lower bound와 upper bound를 정확하게 찾을 수 있습니다.

일반적으로 그래프에서 $p$개의 vertex disjoint cycle을 찾을 수 있다면, $p$는 FVS의 크기에 대한 lower bound가 됩니다. 하지만 그림 1에서처럼 서로 다른 두 vertex disjoint cycle을 찾을 수 없음에도 불구하고 (i.e. $p = 1$) 크기가 2보다 작은 FVS를 찾을 수 없는 경우도 있습니다. 즉, “서로 다른 vertex disjoint cycle의 개수”는 “cycle을 없애기 위한 최소의 정점 제거 횟수”의 완벽한 lower bound는 아닌 모양입니다.

그런데 일반적으로 $p = 1$이라면 크기가 3 이하인 FVS가 존재함을 증명할 수 있습니다. (Lovász, 1965) 일반적으로 vertex disjoint cycle의 최대 개수가 $p$개일 때, 크기가 $f(p)$ 이하인 FVS를 찾을 수 있을까요? 만약 $f(p)$가 $p$보다 많이 크지 않다면 더 유용할 것 같습니다.

Exercise. 그래프에 두 vertex disjoint cycle이 존재하지 않는다면, 크기가 3 이하인 FVS가 존재함을 보이세요. (Hint: 사이클 $C$를 잡으면, $G[V - V(C)]$는 forest입니다)

Theorem. (Erdős–Pósa, 1965) $f(p) = \Theta(p \log p)$. 즉, 어떤 상수 $c_{1}, c_{2}$에 대해 $p$가 충분히 크면 $c_{1} p \log p < f(p) < c_{2}p \log p$.

놀랍게도 $f(p)$가 near-linear에서 크게 벗어나지 않음을 알 수 있었습니다. 이처럼 많은 조합적 구조에서 아래 두 양은 밀접한 관계가 있습니다.

• Vertex Packing: Vertex disjoint subgraph $G_{1}, \cdots, G_{k}$가 각각 해당 구조를 갖는 최대의 $k$를 해당 구조의 vertex packing number라고 부른다.
• Vertex Covering: $\lvert S \rvert = l$인 정점의 집합 $S \subseteq V$ 를 제거하여 $G[V - S]$는 해당 구조가 없도록 할 수 있다면, 가능한 최소의 $l$을 해당 구조의 vertex covering number라고 부른다.

마찬가지로 Edge packing, Edge Covering 간의 관계도 얻을 수 있습니다. 많은 문제들을 이와 같이 Packing-Covering duality의 문법으로 쓸 수 있습니다.

• Cycle Packing / Feedback Vertex Set: 대상이 되는 “구조”는 $C_{n}$ ($n \ge 2$) subgraph 혹은 $C_{3}$ minor로 생각할 수 있습니다.
  • (Vertex) Packing: Cycle을 갖는 vertex disjoint subgraph를 최대 몇 개 찾을 수 있는가?
  • Covering: Cycle이 없으려면 몇 개의 정점을 제거해야 하는가? (FVS)
  • (Multiplicative) Duality gap: $\Theta(\log p)$ where packing number is $p$
• Maximum Matching / Vertex Cover: 대상이 되는 구조를 $P_{2}$ subgraph (i.e. “간선”)으로 생각하면,
  • (Vertex) Packing: vertex disjoint한 $P_{2}$ subgraphs의 최대 개수는? (Maximum Matching)
  • Covering: 남은 그래프에 간선이 없으려면 몇 개의 정점을 제거해야 하는가? (Vertex Cover)
  • Duality gap: $1$ for bipartite graphs (Kőnig’s theorem), $2$ for general graphs
• Tree packing / Edge-connectivity: 대상이 되는 구조를 Spanning tree로 생각하면,
  • (Edge) Packing: Edge-disjoint spanning tree의 최대 개수는? (Tree packing)
  • Covering: 그래프가 disconnected 되려면 몇 개의 간선을 끊어야 하는가? (Edge connectivity / Min Cut)
  • Duality gap: $2$ (Nash-Williams Theorem)

오늘 이야기하고자 하는 문제인 Erdős–Pósa Property 또한 Erdős–Pósa Theorem을 포괄하는 일반적인 개념으로, 비슷하게 Packing-Covering Duality로 쓸 수 있습니다.

Definition (Graph Minor): $G$에서 $H$를 아래 과정 중 하나를 유한 번 반복해서 얻을 수 있다면, $H$를 $G$의 Minor라고 합니다.

1. Vertex Deletion
2. Edge deletion
3. Edge contraction

cf) 1만 허용하는 경우에는 induced subgraph, 2만 허용하는 경우에는 subgraph라고 부릅니다.

Definition (Minor Packing) 그래프 $H$가 주어져 있을 때, 어떤 그래프 $G$의 vertex-disjoint subgraph $\Pi := \lbrace G_{1}, \cdots, G_{k} \rbrace$ 각각이 $H$를 minor로 가지면 $\Pi$를 ($H$-)Minor packing이라고 합니다.

• 가능한 Minor packing의 최대 크기를 Minor Packing Number $\mu_{H}(G)$ 로 정의합니다.

Definition (Minor Covering) 그래프 $H$가 주어져 있을 때, 어떤 그래프 $G$에 대해 $G - S$가 $H$를 minor로 갖지 않는다면 $S$를 ($H$-)minor covering이라고 합니다.

• 가능한 Minor covering의 최소 크기를 Minor covering number $\gamma_{H}(G)$로 정의합니다.

Remark. 당연하게도 $\mu_{H}(G) \le \gamma_{H}(G)$입니다.

Definition. (Erdős–Pósa Properties for Minor class)

만약 어떤 함수 $f : \mathbb{N} \to \mathbb{N}$이 존재하여 $\gamma_{H}(G) \le f(\mu_{H}(G))$가 모든 그래프 $G$에 대해 성립하면, $H$에 대해 Erdős–Pósa Property가 성립한다고 말합니다. 이 때 $f$를 $H$에 대한 Erdős–Pósa function이라고 합니다.

Question. 어떤 그래프 $H$에 대해서 Erdős–Pósa Property가 성립하는가?

우리가 알고 있는 사실은 아래와 같습니다.

Positive Side:

• 만약 $H = C_{3}$라면, $f(k) = \Theta(k \log k)$. (Erdős–Pósa Theorem)
• 만약 $H = P_{2}$라면, $f(k) = 2k$. (max matching $\le$ packing number $\le$ covering number $=$ min vertex cover $\le$ 2 (max matching))

Negative Side:

• 아무것도 모릅니다.

이 글에서는 아래 사실을 증명하겠습니다.

Theorem. $H$에 대해 Erdős–Pósa Property가 성립할 필요충분조건은 $H$가 planar graph인 것이다.

아래 사실은 증명하진 않지만 상당히 흥미롭습니다.

Theorem (Van Batenburg, 2019) 주어진 $H$에 대한 Erdős–Pósa function $f$는 다음과 같다.

• $H$가 forest라면, $f(k) = \Theta(k)$.
• $H$가 이외의 planar graph라면 $f(k) = \Theta(k \log k)$.

Introduction 2 : Treewidths and Grid Minor Theorem

Theorem을 증명하기 위해선 몇 가지 도구가 더 필요합니다.

그래프 $G$의 Tree decomposition이란, 어떤 트리 $T$를 잡아서 $G$의 각 정점 $v \in V(G)$을 $T$의 connected subtree $X(v) \subseteq V(T)$에 대응시킨 것을 말합니다. 이 때, $G$의 두 정점 $u, v$ 사이에 간선이 있으면 반드시 $X(u)$와 $X(v)$가 겹쳐야 합니다.

어떤 트리의 정점 $t \in V(T)$에 대해 bag $B(t) = {v : t \in X(v)}$ 로 정의하면, 이 tree decomposition $(T, X)$의 width는 $\max_{t} \lvert B(t) \rvert - 1$ 로 정의합니다. $G$의 treewidth는 가능한 tree decomposition의 width 중 최솟값으로 정의하고, $\mathbf{tw}(G)$로 표기합니다.

• $G$가 Tree인 경우 항상 treewidth 1짜리 decomposition을 찾을 수 있습니다.
• $\mathbf{tw}(K_{n}) = n - 1$입니다. 나아가 그래프에 크기 $k$의 clique이 있다면 treewidth는 최소한 $k - 1$ 이상이 됩니다.

$m \times n$ 그리드 그래프 $\mathbf{Grid}_{m,n}$을 ${(i, j) : 1 \le i \le m, 1 \le j \le n}$을 정점으로 갖고, $\lvert i _ {1} - i _ {2} \rvert + \lvert j _ {1} - j _ {2} \rvert = 1$ 을 만족하는 두 정점 사이에 간선을 이어준 그래프로 정의합시다.

Proposition. $\mathbf{tw}(\mathbf{Grid}_{m,n}) = \min(m, n)$.

Proof. 편의상 $m \le n$이라고 하면, $m + 1$짜리 tree decomposition을 찾을 수 있습니다. $v _ {(j-1)n + (i-1)} = (i, j)$라고 두면, $(v_{i}, \cdots, v_{i + m})$ 을 bag로 하는 path 모양의 tree decomposition을 만들 수 있습니다.

treewidth가 $m$ 이상이라는 사실은 어떻게 보일까요? Subgraph로 포함되는 $\mathbf{tw}(\mathbf{Grid}_{m, m}) \ge m$만 보이면 충분할 것입니다.

Treewidth의 lower bound로는 Bramble을 많이 사용합니다.

Definition. 그래프 $G$의 connected vertex subset들의 collection $\mathcal{B} = \lbrace \beta _ {i} \rbrace _ {i}$가 다음 조건을 만족하면 $\mathcal{B}$를 bramble이라고 합니다.

• 모든 $i \neq j$에 대해 $\beta_{i}, \beta_{j}$는 공통 원소를 갖거나, $(x, y) \in E \cap (\beta_{i} \times \beta_{j})$가 존재한다.

Definition. vertex set $S \subseteq V(G)$가 모든 $i$에 대해 $S \cap \beta_{i} \neq \emptyset$를 만족하면 $S$를 $\mathcal{B}$의 cover라고 합니다. 가능한 cover의 최소 크기를 bramble $\mathcal{B}$의 order라고 합니다.

Bramble은 영어로 ‘덩굴’인 만큼, tree decomposition에 그렸을 때 아주 복잡하게 얽혀 있습니다. 일반적으로 $X(S) := \bigcup_{v \in S} X(v)$ 로 정의하면, Bramble $\mathcal{B}$의 모든 원소 $\beta_{i}, \beta_{j}$에 대해 $X(\beta_{i}) \cap X(\beta_{j}) \neq \emptyset$이어야 합니다.

Lemma. 그래프 $G$에 order $k+1$의 bramble이 있다면, $\mathbf{tw}(G) \ge k$.

Proof. $\mathbf{tw}(G) < k$라고 가정하고 width가 $k-1$ 이하인 tree decomposition $(T, X)$가 있다고 합시다. 트리 $T$의 어떤 간선 $(s, t) \in E(T)$에 대해서, 두 bag의 교집합 $B(st) := (B(s) \cap B(t)) \subseteq V(G)$는 크기가 $k$ 이하일테니 $\mathcal{B}$를 cover할 수 없습니다. 즉 어떤 bramble의 원소 $\beta \in \mathcal{B}$가 존재해서 $X(\beta) \cap B(st) = \emptyset$이고, $(s, t)$를 제거했을 때 $T$의 두 연결 컴포넌트 (subtree) $T_{s}, T_{t}$ 중 하나에 완전히 포함됩니다. 일반성을 잃지 않고 $X(\beta) \subseteq T_{s}$라고 합시다.

$X(\beta^{\prime}) \subseteq T_{t}$인 $\beta^{\prime} \in \mathcal{B}$는 존재할 수 없습니다. $X(\beta) \cap X(\beta^{\prime}) = \emptyset$이니 bramble의 정의에 모순이기 때문입니다. 따라서 모든 간선 $(s, t)$를 $s$방향 (즉, $B(st)$와 서로소인 bramble이 있는 유일한 방향)으로 orient할 수 있습니다.

$T$는 트리이니 indegree만 있는 정점 $a \in V(T)$가 존재합니다. 이말인즉슨 $B(a) \cap X(\beta) = \emptyset$인 $\beta \in \mathcal{B}$는 존재하지 않습니다. 그랬다면 다른 $a$의 neighbor로 나가는 outdegree가 있었을테니까요. 이는 곧 $B(a)$가 $\mathcal{B}$의 cover라는 뜻이고, $\lvert B(a) \rvert \le k$이니 가정에 모순입니다. $\square$

Proposition. $\mathbf{Grid}_{k, k}$에는 order $k+1$의 Bramble이 존재한다.

Proof. 우선 order $k$의 bramble부터 찾아줍시다.

십자가 $\mathbf{cross} _ {i, j} = \lbrace (k, l) \mid i = k \text{ or } j = l\rbrace$로 두면 이는 connected subset이 되고, $\mathcal{C}_{k} := \lbrace \mathbf{cross} _ {i,j} \mid 1 \le i \le k, 1 \le j \le k \rbrace$도 bramble이라는 것을 알 수 있습니다. 모든 $\lvert S \rvert < k$에 대해 $S$가 덮지 못하는 row $r$과 덮지 못하는 row $c$가 존재하기 마련이고, $\mathbf{cross} _ {r,c} \cap S = \emptyset$이니 $\mathcal{C}$의 order는 $k$입니다.

이제 $\mathcal{C} _ {k}$에 $k+1$번째 row에 해당하는 길이 $k+1$의 horizontal 직선과, $k+1$번째 column에서 $(k+1, k+1)$만 뺀 길이 $k$의 vertical 직선을 더한 것을 $\tilde{C}{k+1}$이라고 합시다. $\tilde{C}{k+1}$는 $\mathbf{Grid}_{k+1,k+1}$의 order $k+2$ bramble임을 쉽게 알 수 있습니다. $\square$

위 Proposition으로부터, $\mathbf{tw}(\mathbf{Grid } _ {k,k}) = k$또한 증명할 수 있습니다. $\square$

$\lbrace \mathbf{Grid} _ {k,k} \rbrace _ {k \ge 1}$는 non-bounded treewidth를 가지면서, 동시에 모든 평면그래프를 Minor로 가집니다.

Proposition. 모든 평면 그래프 $H$에 대해, 상수 $c_{H}$가 존재하여 모든 $k \ge c_{H}$에 대해 $H$는 $\mathbf{Grid} _ {k,k}$의 minor. (증명 생략)

따라서 적당히 큰 Grid를 Minor로 가지려면 treewidth가 커야 합니다. 반대로 treewidth가 충분히 크다면 적당히 큰 Grid Minor를 가질 수 있을까요?

놀랍게도 이는 사실입니다. 이를 Grid Minor Theorem, 혹은 Excluded Grid Theorem이라고 부릅니다.

Theorem (Chekuri, 2016) 다음을 만족하는 상수 $\delta > 1/10$이 존재한다:

모든 treewidth가 $k$보다 큰 그래프는 $\mu = \Omega(k^{\delta})$에 대해 $\mathbf{Grid}_{\mu,\mu}$를 Minor로 갖는다.

Result 1 : Erdős–Pósa Property of Planar graphs

Theorem (If-part) 임의의 평면그래프 $H$는 Erdős–Pósa property를 갖는다. 즉, 임의의 그래프 $G$에 대해 $H$-vertex packing number $\nu_{H}(G) < k$라면, $f(k) = k^{O(1)}$에 대해 $H$-vertex cover $\gamma_{H}(G) < f(k)$가 성립한다.

Recall: $\nu_{H}(G)$는 $G$에서 $H$를 Minor로 갖는 vertex-disjoint subgraph의 최대 개수, $\gamma_{H}(G)$는 $G - S$가 $H$를 Minor로 갖지 않게 하는 $S$의 최소 크기로 정의했습니다.

Proof. 만약 충분히 큰 상수 $C$에 대해 $\mathbf{tw}(G) > Ck^{1/2\delta}$라면, Grid Minor Theorem에 의해 $P \ge (C_{H}+2)\sqrt{2k + 1}$ 에 대해 $\mathbf{Grid} _ {P, P}$를 Minor로 찾을 수 있습니다. 이 안에서는 vertex disjoint한 $k$개의 $C _ {H} \times C _ {H}$ grid를 찾을 수 있고, 각각은 $H$를 Minor로 가질 것입니다.

이제 $\mathbf{tw}(G) \le Ck^{1/2\delta}$인 상황을 봅시다. $O(\mathbf{tw}(G) \log k)$ 개의 정점을 제거하여 $G$에 $H$-minor가 존재할 수 없도록 만들 것입니다.

Tree decomposition을 꽤나 깊이 있게 다루어야 하는데, 이를 위해 tree decomposition 중 편리한 형태를 가정합시다.

Definition. (Nice Tree Decomposition) 모든 Tree decomposition $(T, X)$에 대해서, linear time에 같은 width의 Nice tree decomposition을 찾을 수 있다.

Nice tree decomposition $(T, X)$은 rooted tree로, 모든 노드 $t \in V(T)$는 최대 2개의 자식을 가지며 다음 중 하나로 분류된다.

• Leaf Node: 모든 리프노드는 $B(t) = \emptyset$을 만족한다.
• Join Node: 두 자식 노드 $l, r$을 가지며, $B(t) = B(l) = B(r)$.
• Forget/Introduce Node 유일한 자식 $u$를 가지며, $B(t) = B(u) - \alpha$ (Forget) 혹은 $B(u) = B(t) - \alpha$. (Introduce). 즉, 자식에서 원소 하나를 빼거나 더한 꼴.

또한, 루트 $B(r) = \emptyset$을 만족한다.

Proposition $\nu_{H}(G) = k$이라면, $\gamma_{H}(G) = O(\mathbf{tw}(G) \log k)$.

Nice tree decomposition $(T, X)$와 $t \in T$에 대해, $t$의 subtree를 $S _ {t} \subseteq V(T)$, $G_{t}\subseteq V(G)$를 $X(v) \cap S_{t} \neq \emptyset$인 정점들이라고 합시다.

$k = 1$인 경우, $G_{t}$가 $H$-minor를 갖는 가장 낮은 노드 $t$가 존재합니다. 즉, $t$의 자식 $u$에 대해 $G_{u}$는 $H$-minor를 갖지 않습니다.

조건에 의해 $t$는 Join Node이거나 Introduce Node입니다. 그렇지 않다면 $G_{u} \supseteq G_{t}$인 $t$의 자식 $u$가 존재합니다.

1. $t$가 Join Node인 경우

두 자식을 $l, r$이라고 둡시다. $t$의 정의에 따라 $G_{l}$, $G_{r}$에는 $H$-minor가 존재할 수 없습니다. 이제 $B(t) = B(l) = B(r)$을 제거하면, 그래프에는 다음 정점 중 하나만 남습니다.

• $A$: $X(v) \subseteq S_{l}$인 정점들. $A \subseteq G_{l}$
• $B$: $X(v) \subseteq S_{r}$인 정점들. $B \subseteq G_{r}$
• $C$: $X(v) \subseteq V(T) - S_{t}$인 정점들.

정의에 따라 $A, B$에는 $H$-minor가 없습니다. $C$에 $H$-minor가 있다면 이는 $G_{t}$와 함께 $H$-minor를 갖는 vertex disjoint subset이 되므로 모순입니다. 따라서 $\lvert B(t) \rvert \le \mathbf{tw}(G)+1$ 개의 정점을 제거하여 $H$-minor를 없앨 수 있습니다.

1. $t$가 Introduce node인 경우

마찬가지로 $B(t)$를 제거하면 됩니다. 자세한 증명은 생략합니다.

이제 $k > 1$인 경우, 최대 $\mathbf{tw}(G)$ 개의 정점 $S$를 제거하여 $G - S$를 $\nu _ {H}(C _ {i}) \le \frac{2k}{3}$인 두 집합 $C _ {1}$, $C _ {2}$로 쪼갤 수 있음을 보이면 됩니다.

마찬가지로 $\nu_{H}(G_{t} - B(t)) > \frac{2k}{3}$인 가장 낮은 $t$를 찾으면, $t$는 Join Node이거나 Forget Node입니다. 리프이거나 루트일 수는 없고, Introduce node에서는 $G_{u} - B(u) \supseteq G_{t} - B(t)$이기 때문입니다.

1. $t$가 Join Node인 경우

두 자식 중 $\nu_{H}(G _ {l} - B(t)) > \frac{k}{3}$인 자식 $l$이 존재합니다. $G_{l} - B(t)$와 $G_{r} - B(t)$는 vertex disjoint한 $G_{t} - B(t)$의 partition이니 packing number를 더해서 정확히 같아져야 하기 때문입니다.

이제 $B(t)$를 지우면, $V(G)$의 모든 정점은 $G_{l} - B(t)$ 혹은 $V(G) - V(G_{l})$ 에 속하게 됩니다. $\nu_{H}(G_{l} - B(t)) + \nu_{H}(V(G) - V(G _ {l})) \le k$ 이고 $\frac{k}{3} < \nu _ {H}(G _ {l} - B(t)) \le \frac{2k}{3}$ 이므로 각각은 packing number가 $\frac{2k}{3}$보다 작거나 같습니다.

1. $t$ 가 Forget Node인 경우

$t$의 자식을 $u$라고 하면 $B(u)$를 지웁니다.
$G_{u} - B(u) = (G_{t} - B(t)) - \alpha$이므로 $\nu _ {H}(G _ {u} - B(u)) \ge \nu _ {H}(G _ {t} - B(t)) - 1 > \frac{2k}{3} - 1 \ge \frac{k}{3}$이 성립하고, 따라서 $V(G) - V(G_{u})$ 또한 packing number가 $\frac{2k}{3}$ 이하가 됩니다.

결국 Packing number가 $k$일 때 지우게 되는 정점의 수를 $F(k)$라고 하면, $F(k) \le F(k _ {1}) + F(k _ {2}) + \mathbf{tw}(G) + 1$ 입니다. ($k _ {i} \le \frac{2k}{3}$)

따라서 대략 $O((\mathbf{tw}(G) + 1)\log k)$ 개의 정점만 지우면 $G$에서 $H$-minor가 없도록 할 수 있습니다.

Result 2 : All non-planar graphs are not Erdős–Pósa

Theorem. (Only-if side) $H$가 connected non-planar graph라면, 임의의 $k$에 대해 $\nu_{H}(G) = 1$이고 $\gamma_{H}(G) \ge k$인 그래프 $G$가 존재한다.

Proof. $H$의 각 정점을 아래와 같이 $\mathbf{Grid} _ {d+k+1, dk}$로 바꾼 뒤, 맨 위쪽 (바깥쪽) 줄은 $k$개씩 $d$그룹으로 짝지어 다른 정점의 gadget으로 연결해줍니다. 맨 아래쪽 (안쪽 줄은) $d$개씩 $k$그룹으로 짝지어, 원의 중심에 있는 새로운 점 $a _ {1}, \cdots, a _ {k}$ 로 이어줍니다.

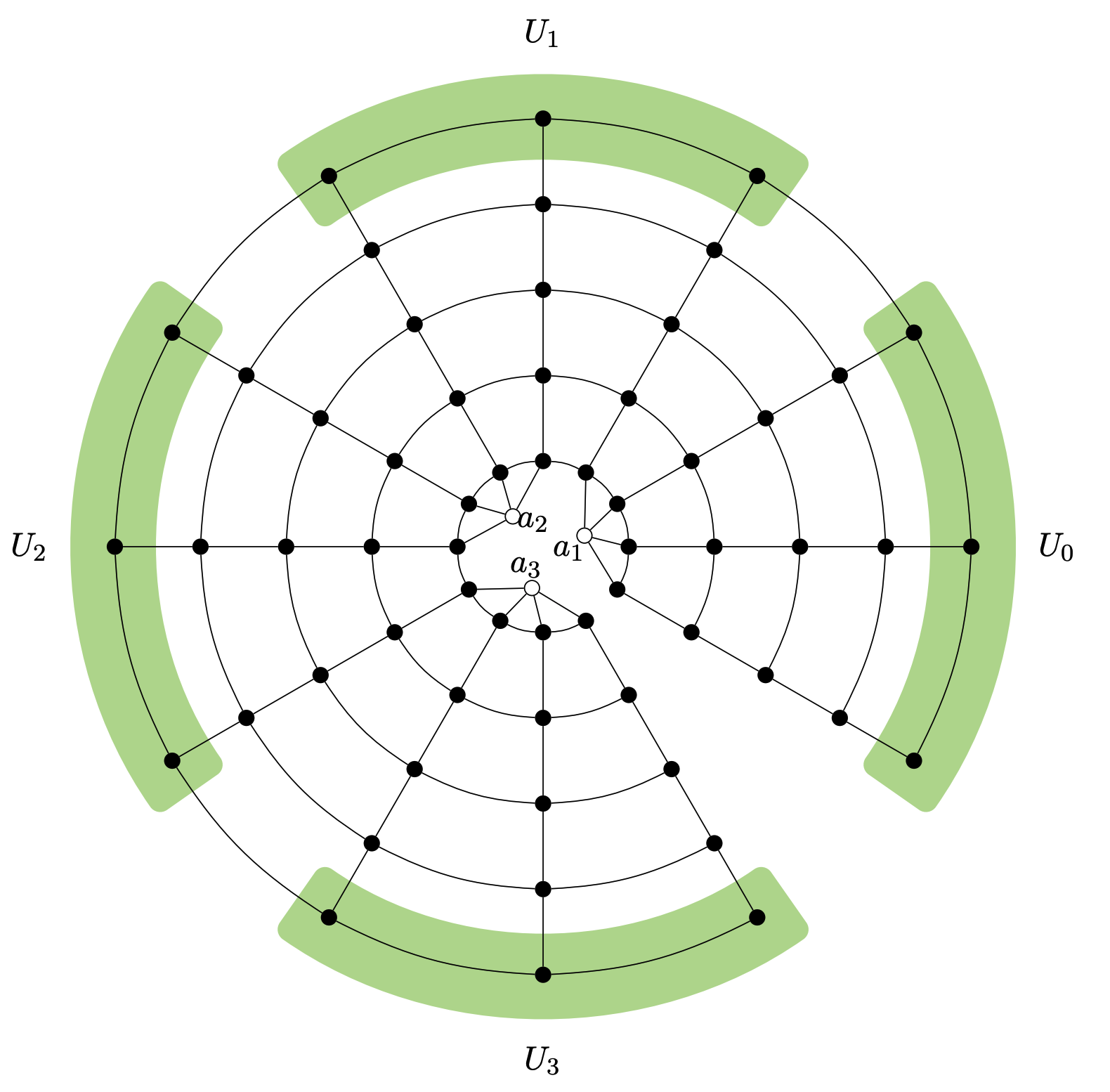
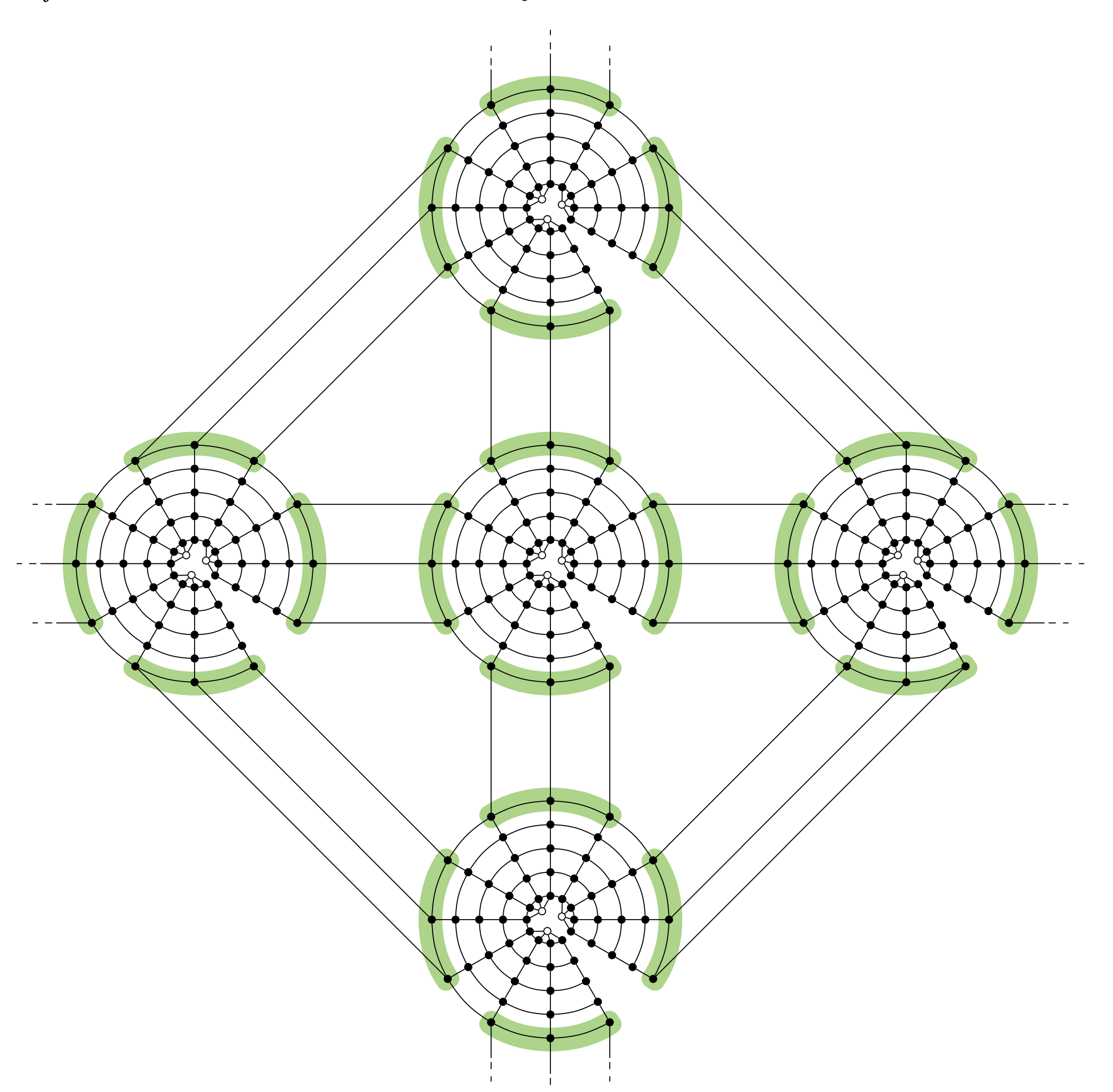
gadget을 한 점으로 줄일 수 있으므로 이 그래프는 $H$를 minor로 가집니다. 하지만, 이 그래프는 $H$와 정확히 같은 Euler genus를 가집니다. 만약 그래프에 서로 다른 $H$-minor가 있다면, $H$의 non-planarity에 의해 이 그래프는 동일한 genus surface에 그릴 수 없습니다. 따라서 $\nu _ {H} (G) = 1$을 증명할 수 있습니다.

한편, 그래프에서 $k$ 개 미만의 정점을 제거하면, gadget에는

• 최소 하나 이상의 $a _ {i}$와, 그에 이웃한 맨 아랫줄의 정점
• 최소 $d$ 개 이상의, 아무 정점도 지워지지 않은 row
• 최소 $(d-1)k + 1$ 이상의 아무 정점도 지워지지 않은 column
• 맨 윗줄의 각 그룹 (녹색 띠) 마다, 지워지지 않은 하나 이상의 정점 이 남아 있고, 이로부터 $H$-minor를 여전히 만들 수 있습니다. 따라서 $\gamma_{H}(G) \ge k$ 이상이 됩니다. $\square$

Conclusion

이 글을 통해 planar graph의 경우 vertex minor packing이 $k$ 이하이면 약 $O(k^{5} \log k)$ 개의 정점을 제거하여 해당 그래프를 minor로 갖지 않게 할 수 있다는 정리를 보일 수 있었습니다. 언뜻 커 보이지만 그래프의 크기에 의존하지 않는다는 점이 중요합니다.

말씀드린대로, Erdős–Pósa function의 bound는 현재 $\Theta (k \log k)$입니다. Grid Minor Theorem의 경우 $k \times k$ grid를 minor로 갖지 않는 $\Omega(k^{2} \log k)$ treewidth짜리 그래프가 존재하고, treewidth $\Theta(k^3)$이 best possible일 것으로 믿어지고 있습니다. (Demaine, 2013) 따라서 Grid Minor Theorem으로 해당 bound를 좁히기는 무리가 있고, 더 정교한 tool들을 사용합니다.

이 글을 통해 Bounded treewidth graph에서 packing-covering duality를 다루는 방법과 grid minor theorem 등 여러 중요한 부분을 다루었는데요, treewidth에 대해서 보다 문제 풀이에 가까운 설명이 필요하다면 이 글을 참고해주시면 좋을 것 같습니다. 긴 글 읽어주셔서 감사합니다.

References

• (Cao, 2017) Cao, Yixin. “A naive algorithm for feedback vertex set.” arXiv preprint arXiv:1707.08684 (2017).
• (Lovász, 1965) Lovász, László. “On graphs not containing independent circuits.” Mat. Lapok 16.289-299 (1965): 7.
• (Erdős–Pósa, 1965) Pósa, L. “On independent circuits contained in a graph.” Canadian Journal of Mathematics 17 (1965): 347-352.
• (Van Batenburg, 2019) Van Batenburg, Wouter Cames, et al. “A tight Erdős-Pósa function for planar minors.” Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics, 2019.
• (Chekuri, 2016) Chekuri, Chandra, and Julia Chuzhoy. “Polynomial bounds for the grid-minor theorem.” Journal of the ACM (JACM) 63.5 (2016): 1-65.
• (Demaine, 2006) https://erikdemaine.org/papers/GridWagner_ISAAC2006/paper.pdf