Coldgame in problem solving
Intro
알고리즘 대회에 출전하거나 문제를 해결하다보면 게임을 하는 게임이론 문제를 가끔씩 만나볼 수 있습니다. 또한, 이러한 문제에 등장하는 게임은 다양한 분류가 가능하며 그 분류에 따라서 문제를 해결할 수 있는 방법도 가지각색입니다.
이 글에서는 여러분에게 조금은 더 친숙한 님 게임과 Sprague-Grundy Theorem이 아닌 Coldgame 이라는 것에 대해서 problem solving(이하 PS)의 관점에서 소개하고, 문제를 푸는 방법까지 설명하려고 합니다.
About
Coldgame은 Combinatorial game theory에서 Temperature에 따라 분류된 게임의 한 종류입니다. 위 문장의 각각에 대해서 설명하면 아래와 같습니다.
- Combinatorial game에서는 보통 둘이서 하는 것을 가정으로 하며 모든 정보가 모두에게 제공되어지고, 확률의 게입은 고려하지 않습니다.
- 대표적으로는 체스, 바둑, 틱택토 등이 해당됩니다.
- PS에서의 Combinatorial Game theory 문제는 보통 플레이어들이 최선의 플레이를 하는 것을 가정하며, 게임에는 상태가 존재하며, 각 플레이어는 턴을 가지고 자신의 턴에 게임의 상태를 변화시키는 행동을 합니다.
- 수학적으로나 상황적으로 엄밀하지 않을 수 있으나, 본 글에서는 이렇게 분류하도록 하겠습니다.
- Temperature은 보통 각 플레이어가 할 수 있는 행동이 다를 때 사용되어지는 개념이며, 각 플레이어의 가치나 유리한 정도(이하 유리도라 표기) 같은 척도를 나타낼 때 사용되어집니다.
- 이 중에서 Coldgame이라 함은, 각 플레이어가 자신의 턴을 진행함에 따라서 자신에게 무조건 불리하게 작용되어지는 게임을 뜻합니다. 즉, 어떠한 상황에서 게임을 이길 수 없는 플레이어는 자신이 한 번 턴을 진행한 후에 그 게임을 시작할 때 절대로 승리할 수 없습니다.
Nim Game과 다른 점은 자신이 할 수 있는 행동이 서로 구분되어 있어, 내가 행동을 하는 것이 자신에게만 불리하게 작용한다는 것입니다.
Example
Coldgame에 분류 될 수 있는 간단한 게임의 예시를 한 가지 들자면 아래와 같습니다.
- 빨간색 돌과 파란색 돌로 이루어진 돌탑이 여러개 쌓여있습니다.
- 자신의 차례에 플레이어 A는 빨간색 돌 한개를 제거하며, 플레이어 B는 파란색 돌 하나를 제거합니다.
- 모든 플레이어는 돌탑에서 가장 위에 있는 돌만 제거할 수 있습니다.
- 자신의 턴에 행동을 할 수 없는 플레이어가 패배합니다.
위와 같이 한 플레이어가 행동함에 따라서 상대방이 행동할 수 있는 범위는 변화할 수 있으나, 자신이 플레이 한 후의 게임의 상태는 자신에게 무조건 더 불리한 상태가 됩니다.
How to Solve
PS에서의 Coldgame은 보통 상황이 주어졌을 때 누가 승리할 것인지를 물어보는 문제가 많으며 이를 해결하는 과정은 아래와 같습니다.
- 주어진 문제의 게임 상황을 여러개의 묶음으로 분리합니다. 행동을 했을 때 영향을 받는 것들끼리 묶을 수 있으며, 위와 같은 문제에서는 하나의 돌탑이 하나의 묶음처럼 작용할 것입니다.
- 각 묶음에 대해서 유리도를 계산합니다. 보통 자유롭게 한 번 행동이 가능할 때의 유리도를 1로 계산하며 플레이어 A가 유리한 경우 +x, B가 유리한 경우 -x로 생각합니다.
- 모든 묶음의 유리도를 더합니다. 이후 계산결과가 양수면 A가, 음수면 B가, 0이면 후공이 승리합니다.
결국 각 문제별로 해결해야하는 부분은 2번입니다. 이때 각 묶음의 유리도를 계산하는 과정에서 3번의 도움을 받을 수 있습니다.
예를 들어 묶음 X 2개와 +1의 유리도인 묶음 Y가 있는 게임에서 후공이 승리하는 상황이라면, 묶음 X의 유리도는 -0.5라고 생각할 수 있습니다.
문제 : UCPC 2023 K - 그건 가지가 아니라 대파예요
문제
아래의 사진과 같은 크기 $N$ 행 $M$ 열 게임판이 주어진다. $2 \le N, M \le 2500$
플레이어 A는 자신의 차례에서 왼쪽 칸이 ‘가’이고 오른쪽 칸이 ‘지’인 가로 방향으로 인접한 두 타일을 선택하여 해당 두 칸을 ‘대‘, ‘파’로 바꿀 수 있다. 플레이어 B는 자신의 차례에서 위쪽 칸이 ‘대’이고 아래쪽 칸이 ‘파’인 세로 방향으로 인접한 두 타일을 선택하여 해당 두 칸을 ‘가’, ‘지’로 바꿀 수 있다.
자신의 차례에 행동을 할 수 없는 사람이 패배할 때, 주어진 게임판에서 누가 승리할지 구하여라.

풀이
위의 문제는 Coldgame으로 분류되는 게임의 형태이므로, 설명한 방법을 통해 문제를 해결할 수 있다.

‘가’나 ‘대’ 같은 경우는 오른쪽칸과 아래쪽 칸과만 상호작용하며, ‘지’나 ‘파’ 는 왼쪽칸과 윗칸과 상호작용하기 때문에 이를 고려하여 게임판을 묶음으로 분류하면 위의 게임판과 같이 묶을 수 있다.
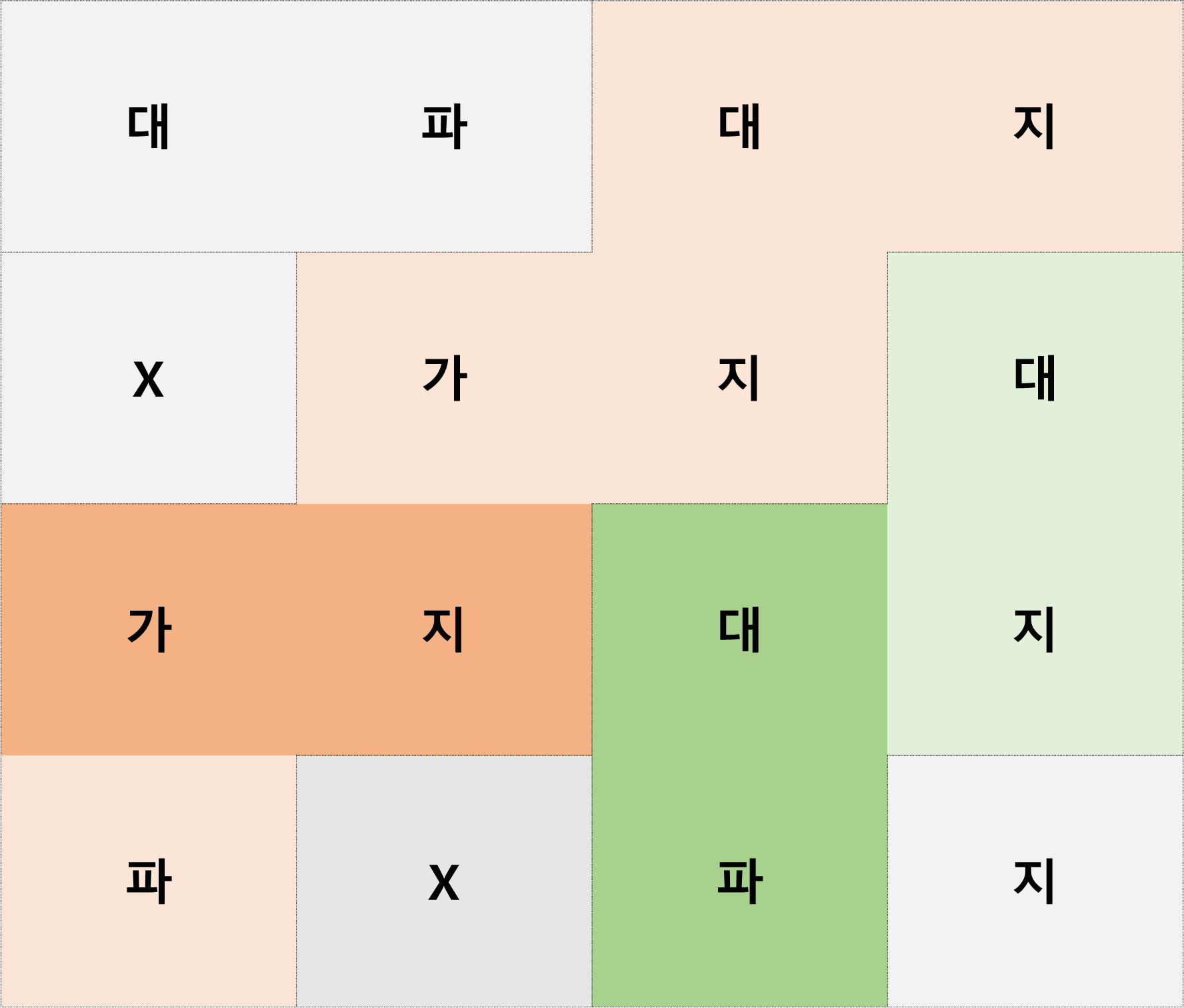
이후 각 묶음에서 유리도를 구하기 위해서 왼쪽 아래서부터 그리디하게 생각할 것이다. 먼저 연두-초록 묶음에서는 초록으로 칠한 대파부분을 플레이어 B가 무조건 바꾸는 것이 이득이다. 묶음의 가장 왼쪽 아래이므로 아래의 칸이 ‘지’로 바뀌는 것은 손해가 없으며, ‘대’가 ‘가’로 바뀌어 가지가 하나 나온다고 해도 상대가 또 바꾸면 +-0 에 ‘지’만 ‘파’로 바뀌어 이득을 보게 된다.
이와 반대로 주황색 묶음의 진하게 칠한 가지는 바꾸지 않는 것이 맞다. ‘가’아래 ‘파’가 존재하기 때문에 상대는 바로 바뀐 ‘대’를 이용하여 대파를 가지로 바꿀 것이며, 이렇게 되면 오른쪽의 ‘지’만 ‘파’로 바뀌어 A입장에서 손해를 보게 된다. 다만 가장 왼쪽 아래의 ‘파’ 왼쪽에 ‘가’ 가 있었다면 다시 가지는 바꾸는 것이 이득이 된다. 여기서 추가적으로 생각하면 연결된 가와 파를 상쇄시킬 수 있다는 것도 생각할 수 있다. 이런식으로 각 묶음별로 한 쪽에서부터 그리디하게 바꿔나가면 그 묶음의 유리도를 계산할 수 있다.
또한 공식 풀이 설명에서는 이 문제를 돌을 옮기는 문제로 바꾸어 생각하였으며, 좀 더 편하게 각 묶음의 유리도를 계산할 수 있도록 설명하였다.
최종적으로 이렇게 계산한 유리도를 모두 더하여 0이하인지 아닌지에 따라서 답을 출력하면 된다. 총 시간 복잡도 $O(NM)$ 에 해결할 수 있다.
추가 문제
아래의 문제들 역시 Coldgame으로 분류가 되며, 위와 같은 일련의 풀이방식을 거쳐 해결할 수 있다.
아래 문제인 Black and White Boxes는 Coldgame 중에서도 특수한 분류에 속해있으며, 이에 관해서는 추후에 다룰 예정이다.