January 27, 2025 00:00

Cartesian Tree

Cartesian Tree는 대소 관계가 있는 값의 배열으로부터 유도되는 Binary Tree로, 구간의 min/max와 관련된 문제에 사용하면 편리한 자료 구조입니다.

배열의 최솟값 또는 최댓값에 해당하는 인덱스를 루트로 하게 되는데, Min Cartesian Tree의 경우 최솟값에 해당하는 $\mathrm{array}[i] = \min_{l \leq i \leq r}(\mathrm{array}[i])$인 $i$가 루트가 되며, $[l, r]$번째 원소의 최솟값에 대응되는 노드 $i$의 왼쪽 자손은 $[l, i-1]$에서의 최솟값, 오른쪽 자손은 $[i+1, r]$에서의 최솟값에 해당하는 인덱스가 됩니다.

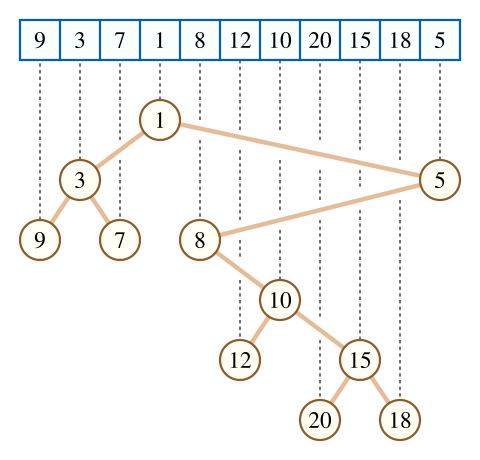
자주 사용하게 되는 성질 몇 가지가 있는데, 각 노드의 subtree가 곧 그 노드가 관리하게 되는 구간(그 노드의 값이 min/max가 되는 가장 넓은 구간)이 되고, 두 노드의 LCA가 곧 그 사이 구간에서의 Range min/max가 됩니다.

위의 정의 그대로 Sparse Table 등을 이용해서 RMQ를 반복하면 $O(N \mathrm{log} N)$에 구할 수 있지만, Monotonic Stack을 이용하여 $O(N)$에 구성할 수도 있습니다. 아래 코드는 Stack을 이용하여 Min Cartesian Tree를 구성하게 되며, $\mathrm{child}[i]$는 노드 $i$의 (왼쪽 자손, 오른쪽 자손)의 위치를 나타냅니다. 참고로, $\mathrm{array}[i]$ 중 서로 같은 값이 있을 수 있으므로, $(\mathrm{array}[i], i)$의 쌍을 하나의 값으로 보며 비교한다고 생각합니다.

int root = 1;
std::stack<int> st;
std::vector<std::pair<int,int>> child(n+1);
for(int i=1;i<=n;i++){
    while(!st.empty() && arr[st.top()] > arr[i]){
        child[i].first = st.top();
        st.pop();
    }
    if(!st.empty()) child[st.top()].second = i;
    st.push(i);
    if(arr[i] < arr[root]) root = i;
}

반대로 $\mathrm{child}$ 대신 $\mathrm{parent}$를 구하는 것이 편한 경우 아래와 같이 구하면 됩니다. 한쪽을 구하면 다른 한쪽은 반복문으로 간단하게 구할 수 있으므로 편한 쪽을 사용하면 됩니다.

int root = 1;
std::stack<int> st;
std::vector<int> parent(n+1);
for(int i=1;i<=n;i++){
    while(!st.empty() && arr[st.top()] < arr[i]){
        if(arr[parent[st.top()]] > arr[i]) parent[st.top()] = i;
        st.pop();
    }
    if(!st.empty()) parent[i] = st.top();
    st.push(i);
    if(arr[i] < arr[root]) root = i;
}

참고로, Cartesian Tree라는 이름은 같은 구조의 Binary Search Tree (Treap)에서도 혼용되어 사용되고 있는데, 이 글에서의 Cartesian Tree는 위의 정의대로 Heap Property를 만족하며 In-order traversal의 결과가 원래 배열과 일치하는 Binary Tree만을 지칭합니다.

이제 몇 가지 문제를 분석하고 Cartesian Tree를 이용하여 해결해 볼 것입니다. 아래 문제들 이외에도 많은 경우에 사용할 수 있겠지만, Solved.ac에서 Cartesian Tree라는 태그로 검색하면 지나치게 어려운 문제가 나오니 주의해야 합니다.

2020 Central European Olympiad in Informatics 1-1 - Fancy Fence

순서대로 높이와 너비가 $(h_i, w_i)$ 인 직사각형 $N$개로 이루어진 히스토그램이 주어질 때, 히스토그램 내부의 격자 직사각형의 개수를 세는 문제입니다. $N \leq 100\,000$ 이고 각각의 $h_i, w_i \in [1, 10^9]$ 입니다.

어떤 격자 직사각형은 $[x_1, x_2] \times [y_1, y_2]$로 나타낼 수 있고, 위쪽 변의 위치 $y_2$를 고정하면 높이가 $y_2$ 이하인 $x_1, x_2$의 범위를 알 수 있기 때문에 개수를 세기 쉬워집니다.

$h[i]$에 대한 Min Cartesian Tree를 구성하고 각각의 노드 $i$가 최소 $h[i]$인 범위(subtree)가 $[left, right]$이라 합시다. 노드 $i$에서 $x_1, x_2$가 $[left, right]$번째 직사각형 사이에 있고 $h[\mathrm{parent}[i]]+1 \leq y_2 \leq h[i]$, $y_1 \leq y_2$인 직사각형을 세면 겹치지 않게 모두 셀 수 있습니다.

이때 각각의 노드에서 개수를 $O(1)$에 셀 수 있으므로 Cartesian Tree 구성과 카운팅 모두 $O(N)$에 처리할 수 있습니다. 저는 Tree임을 강조하기 위해 굳이 Parent, Child 배열을 둘 다 만들고 재귀적으로 구현했지만, 더 단순하게 구현해도 됩니다.
https://www.acmicpc.net/source/share/0e3153f7c8554012b155cfed685bd2b3

Codeforces Round 833 (Div. 2) - E. Yet Another Array Counting Problem

길이가 $N$인 정수 배열 $a$가 주어질 때, $a$와 모든 구간에서 leftmost maximum이 일치하는 정수 배열 $b$의 개수를 세는 문제입니다. 즉, 모든 구간 $[l, r]$에 대해 $k \in [l, r]$이고 $array[k] = \max_{l \leq i \leq r}(array[i])$이면서 가장 왼쪽인 $k$의 위치가 $a$와 $b$에서 일치해야 합니다. $b[i]$ 값은 $[1, M]$에서 자유롭게 선택할 수 있습니다. $2 \leq N, M \leq 200\,000$이고 $N \times M \leq 1\,000\,000$입니다.

문제의 조건은 배열 $a$와 $b$에서 Max Cartesian Tree가 일치하는 것과 동치이므로, Cartesian Tree 위에서의 $\mathrm{DP}$를 정의하여 해결할 수 있습니다.

$\mathrm{DP}(i, j)$:=$i$의 서브트리를 $1$ ~ $j$로 채우는 경우의 수

$\mathrm{DP}(i, j) = \mathrm{DP}(i, j-1) + \mathrm{DP}(l, j-1) \times \mathrm{DP}(r, j)$

모든 계산을 $O(N \times M)$에 처리할 수 있습니다.
https://codeforces.com/contest/1748/submission/301128231

이 문제와 설정이 거의 비슷하지만 $b[i]$의 합의 기댓값을 구해야 하는 문제도 있으니 위의 내용을 이해했다면 풀어 보시기를 추천드립니다.
https://www.acmicpc.net/problem/18984

Codeforces Global Round 28 - F. Kevin and Math Class

길이가 $N$인 정수 배열 $a$, $b$가 주어지고, 모든 $a[i]$ 값을 $1$로 만드는 것이 목표입니다. 한 번의 “조작”은 구간 $[l, r]$을 선택하여 $l \leq i \leq r$에서 $a[i] = \lceil \frac{a[i]}{\min_{l \leq i \leq r}(b[i])} \rceil$로 변경할 수 있습니다. 모든 $a[i]$ 값을 $1$로 만들기 위한 최소한의 “조작” 횟수를 구해야 합니다. $N \leq 200\,000$이고 $a[i], b[i] \leq 10^{18}$입니다.

우선, $[1, N]$에 대해 조작을 $log_2(\max_{1 \leq i \leq N}a[i]) \leq 60$번 시행하면 항상 모든 $a[i]$가 $1$이 되므로 답은 항상 $60$ 이하입니다. 따라서, 조작 횟수를 인자로 하여 다음과 같이 $\mathrm{DP}$ 식을 세울 수 있습니다:
$ \mathrm{DP}(i, j)$:=노드 $i$에 대응되는 구간 내에서 $j$번의 조작을 수행할 때 $\max_{l \leq i \leq r}(a[i])$의 가능한 최솟값

Min Cartesian Tree에서 $i$의 자손을 $l, r$이라 하면 $\mathrm{DP}$ 상태 전이를 아래와 같이 수행할 수 있습니다.

1. $i$를 포함하는 구간을 선택한 경우, $b[i]$가 구간 내 최소이므로,
   $ \mathrm{DP}(i, j) = \lceil \frac{\mathrm{DP}(i, j-1)}{b[i]} \rceil$

2. $i$를 포함하지 않는 구간만을 선택한 경우, 양쪽에서 합쳐서 $j$번 선택하므로,
   $ \mathrm{DP}(i, j) = \min_{0 \leq k \leq j} \max \left( \mathrm{DP}(l, k), \mathrm{DP}(r, j-k),a[i] \right) $

즉, $A=log_2(\max_{1 \leq i \leq N}a[i])$라 할 때 $O(N \times A^2)$ 번의 연산으로 모든 $\mathrm{DP}$ 값을 얻을 수 있습니다.
https://codeforces.com/contest/2048/submission/301126361

이 문제에서 반드시 필요하지는 않지만, $\mathrm{DP}(i)$의 단조성을 이용하여 양쪽의 $\mathrm{DP}$ 값을 합치면 $O(N \times A)$번의 연산만으로 해결 가능합니다.

JOI 2019/2020 Spring Training Camp 3-1 - Constellation 3

너비와 높이가 $N$인 히스토그램이 주어지고 $M$개의 별의 좌표와 가중치 $(X_i, Y_i, C_i)$가 주어집니다. 어떠한 두 별을 포함하면서 히스토그램과 겹치지 않는 직사각형이 존재하지 않도록 별을 제거하려 하는데, 제거된 별의 가중치의 총합을 최소화해야 합니다. $N, M \leq 200\,000$이고 $X_i, Y_i \in [1, N]$, $C_{i} \leq 10^9$입니다.

우선 별을 지우는 대신에 Maximum Independent Set의 가중치의 합을 최대화하는 문제로 변경해서 생각합시다. 앞선 문제들과 마찬가지로 노드 $i$가 $H[i]$를 높이의 최댓값으로 하는 가장 넓은 구간을 나타낸다고 생각하면 상태 전이가 간단해집니다. 빌딩의 높이에 대한 Max Cartesian Tree를 구성하고 다음과 같은 $\mathrm{DP}$를 정의하면 $O(N^2)$에 풀 수 있습니다:
$\mathrm{DP}(i, j)$:=$i$의 서브트리 내에서 높이 $j$ 이하의 별만 고려할 때 가중치 합의 최댓값

1. 높이 $j$인 별을 선택하지 않는다면,
   $ \mathrm{DP}(i, j) = \mathrm{DP}(i, j-1)$

2. $(i, j, C)$인 별을 선택한다면,
   $ \mathrm{DP}(i, j) = \mathrm{DP}(l, H[i]) + \mathrm{DP}(r, H[i]) + C$

3. $i$의 왼쪽에서 높이 $j$인 별을 선택한다면,
   $ \mathrm{DP}(i, j) = \mathrm{DP}(l, j) + \mathrm{DP}(r, H[i])$

4. $i$의 오른쪽에서 높이 $j$인 별을 선택한다면,
   $ \mathrm{DP}(i, j) = \mathrm{DP}(l, H[i]) + \mathrm{DP}(r, j)$

이 풀이를 제출하면 $N, M \leq 2\,000$에 해당하는 $35$점을 받을 수 있습니다.
https://www.acmicpc.net/source/share/7272c19877314e9288ad338a6841acf3

남은 $65$점을 받기 위해서는 $N^2$개보다 적은 상태만으로 문제를 해결해야 합니다. 여러 가지 풀이가 가능하므로 직접 생각해보시는 것을 추천드립니다.

결론

구간에서의 최대, 최소와 관련된 문제가 복잡해지면 Monotonic Stack의 구조가 헷갈리는 경우가 많은데, 이럴 때 Cartesian Tree를 사용하여 직관적으로 상태를 정의할 수 있었습니다. Cartesian Tree를 구성하는 과정만 대략적으로 익혀 두면 다양한 문제에 적용해 볼 수 있을 것입니다.

감사합니다.