개요
LCS(Longest Common Subsequence) 문제는 두 문자열의 공통 부분 수열 중 가장 긴 것을 찾는 문제로, 컴퓨터과학에서 가장 고전적이면서 중요한 문제 중 하나입니다. 이 글에서는 이 문제를 해결하는 간단한 Dynamic Programming 해법부터, 이것의 공간 복잡도를 개선한 Hirschberg 알고리즘과, 일반적인 문자열에서 더 효율적인 Hunt-Szymanski 알고리즘을 소개할 것입니다. 그리고 이들을 비트 집합을 이용해 더욱 최적화하는 방법을 다룰 것입니다.
간단한 DP 해법
$DP[i][j]$를 $A$의 길이 $i$인 접두사와 $B$의 길이 $j$인 접두사의 LCS 길이로 정의하면 다음과 같은 점화식으로 $A$와 $B$의 LCS 길이를 구할 수 있습니다. ($A$, $B$의 길이는 각각 $n$, $m$입니다.)
\[DP[i][j]= \begin{cases} 0 & \text{if }i=0\space or\space j=0 \\ DP[i-1][j-1]+1 & \text{if }A[i]=B[j] \\ max(DP[i-1][j], DP[i][j-1]) & \text{otherwise } \end{cases}\]이 방법으로 LCS의 길이뿐 아니라 실제 LCS중 하나를 찾을 수 있습니다. $DP[0\dots n][0\dots m]$을 모두 채운 뒤 $(i, j)=(n, m)$에서 시작하여 $A[i]$와 $B[j]$가 같으면 $(i-1, j-1)$로 이동하면서 $A[i]$를 지금까지 찾은 LCS의 앞쪽에 붙입니다. $A[i]$와 $B[j]$가 다르면 $(i-1, j)$과 $(i, j-1)$ 중 $DP$ 테이블의 값이 더 큰 곳으로 이동합니다. 이를 $i$와 $j$ 중 하나가 0이 될 때까지 반복하면 됩니다.
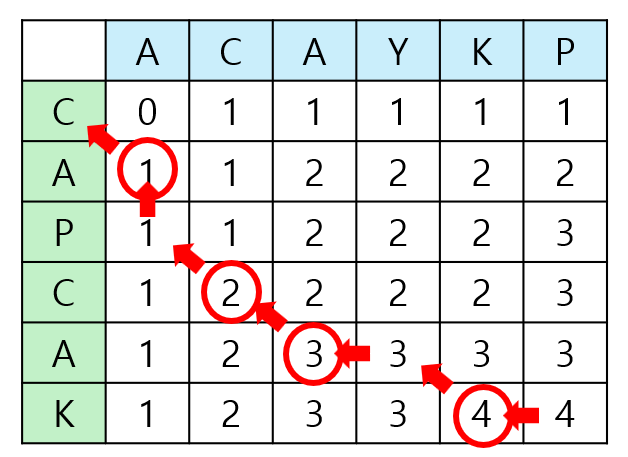
이 방법으로 LCS를 찾기 위해서는 $O(nm)$ 크기의 $DP$ 테이블을 저장해야 합니다. 사실 LCS의 길이만을 찾기 위해서는 $DP[i][j]$의 값을 얻기 위해 $DP[i][?]$ 또는 $DP[i-1][?]$의 값만 참조하면 되므로 토글링 기법을 활용해 $O(n)$ 또는 $O(m)$ 크기의 공간만 있으면 됩니다. 그렇다면 LCS의 길이 정보를 이용해 LCS를 하나 구성할 수 있으면 공간 복잡도가 개선된 알고리즘을 얻을 수 있습니다.
Hirschberg 알고리즘
Hirschberg 알고리즘은 공간 복잡도를 개선하기 위해 분할 정복을 사용합니다. 두 문자열을 두 부분으로 각각 나누어서 앞쪽 쌍과 뒤쪽 쌍의 LCS를 찾은 다음 합치는 것을 반복합니다. 여기서 중요한 것은 두 문자열을 어떻게 나눌지입니다.
분할 정복으로 문제를 해결할 때, 주로 사용하는 방법은 크기가 같은 문제들로 N등분하는 것입니다. 이 문제에서도 비슷하게 두 문자열을 각각 반으로 나누는 방법을 떠올릴 수 있습니다. 그러나 $aabb$와 $bbaa$ 라는 간단한 반례가 있습니다. 두 문자열의 LCS 길이는 2이지만 앞쪽 절반과 뒤쪽 절반 사이에는 LCS가 존재하지 않습니다.
그렇다면 $A$는 반으로 나누되 $B$는 정답을 보장하는 적절한 위치에서 나누면 될 것입니다. 여기서 중요한 것은 “적절한 위치”를 고르는 것이고, 이때 토글링 DP가 사용됩니다. $A$를 $A_l=A[1\dots \lfloor \frac{n}{2} \rfloor]$, $A_r=A[\lfloor \frac{n}{2} \rfloor+1\dots n]$ 두 부분으로 나눈 다음, $A_l$과 $B$의 LCS 길이를 토글링 DP로 구해 $L$ 배열에 저장합니다. 마찬가지로 $A_r^R$과 $B^R$의 LCS 길이도 구해서 $L^\prime$에 저장합니다.($A^R$은 문자열 $A$를 뒤집은 것입니다.) 다음 $0$부터 $n$까지의 $i$ 중에서 $L[i]+L^\prime [n-i]$이 가장 큰 $i$를 구해서 이 위치를 기준으로 $B$를 $B_l=B[1\dots i]$, $B_r=B[i+1, m]$으로 나누면 됩니다.
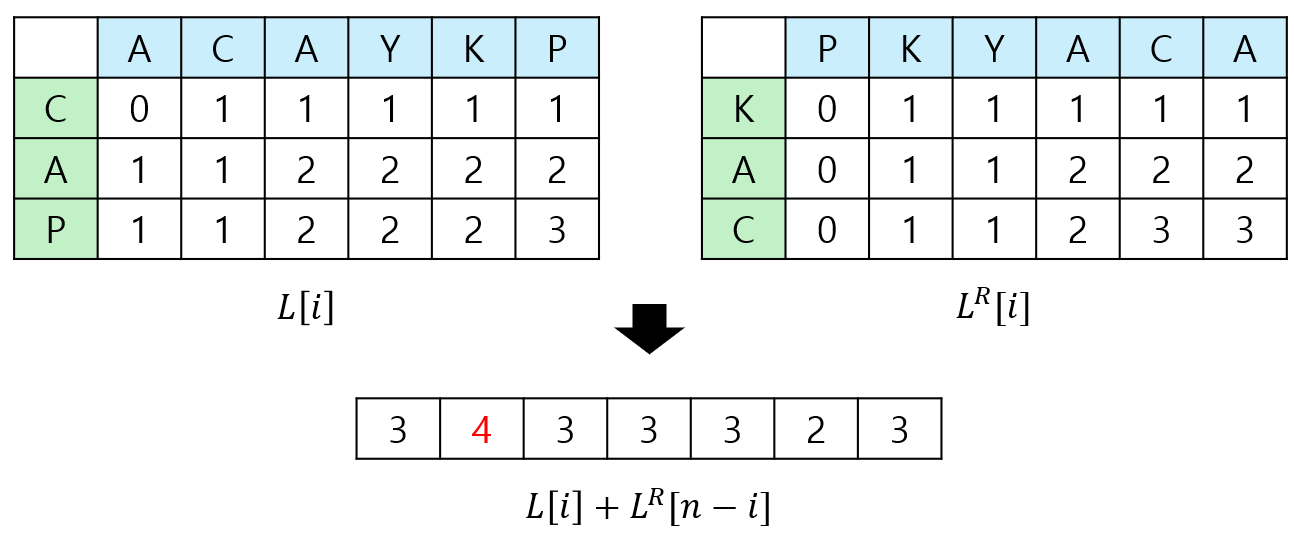
이렇게 나누어진 문자열 쌍의 LCS를 구하는 함수를 재귀적으로 호출합니다. $H(A, B)$는 내부에서 $H(A_l, B_l)$과 $H(A_r, B_r)$을 순차적으로 호출합니다. 이것을 두 문자열 중 하나의 길이가 $1$이 될 때까지 반복합니다. 길이가 $1$인 문자열이 다른 문자열에 포함되어 있다면 해당 문자열을 반환하고, 그렇지 않다면 NULL을 반환합니다. 반환된 문자열을 계속해서 합치면 LCS를 하나 구성할 수 있습니다.
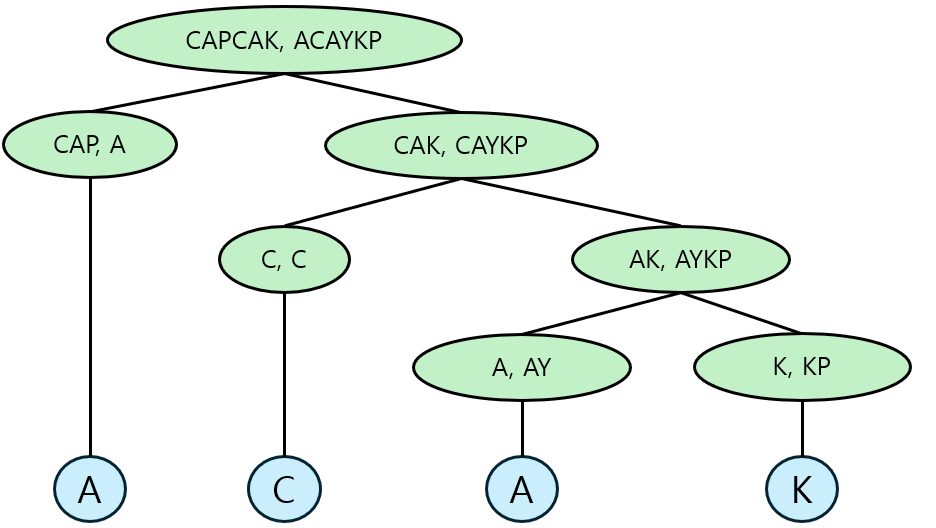
적절한 위치를 찾는 과정에서 연산 횟수는 LCS를 찾으려는 두 문자열의 길이의 곱에 비례합니다. 그리고 $\vert A_l\vert \vert B_l\vert + \vert A_r\vert \vert B_r\vert\leq \lceil \frac{n}{2} \rceil\times (\vert B_l\vert+\vert B_r\vert)=\lceil \frac{n}{2} \rceil\times m$입니다. 그러므로 재귀 함수의 깊이가 하나 증가할 때마다 연산 횟수는 절반으로 줄어듭니다. 따라서 시간 복잡도를 계산하면 $O(nm+\frac{nm}{2}+\frac{nm}{4}+\cdots)=O(nm)$입니다. 시간 복잡도는 위의 DP 해법과 같지만, 공간 복잡도는 크게 향상되었습니다. 토글링 DP를 위한 공간과 정답을 저장하기 위한 공간으로 $O(min(n, m))$만의 공간을 확보하면 됩니다. 여기에 $A$, $B$를 저장하기 위한 공간으로 $O(n+m)$이 필요하므로, 공간 복잡도는 총 $O(n+m)$입니다.
Bitset을 이용한 최적화
위의 DP 테이블에서 각 행과 열의 원소들은 단조성을 가지고, 인접한 원소의 차이는 최대 1임을 관찰할 수 있습니다. 그러므로 인접한 원소의 차를 저장하면 그것들을 bitset으로 관리할 수 있습니다. 비트 연산들의 조합으로 여러 개의 비트들을 한 번에 계산할 방법이 있다면 연산 횟수를 $O(\frac{nm}{64})$으로 크게 줄일 수 있습니다.
인접한 원소를 저장하는 테이블 $L$을 $L[i][j]=DP[i][j]-DP[i-1][j], 1\leq i\leq n, 1\leq j\leq m$으로 정의합니다. 그리고 $L^\prime$을 $L$의 원소들을 반전시킨 것으로 정의합니다. $L$의 column을 하나의 bit vector으로 간주할 것이므로 $L[i][j]$를 $L[j]_i$으로 표기하겠습니다. 그리고 bit vector $M$은 각 문자에 대해 해당 문자가 $A$의 각 인덱스에 있는 문자들과 일치하는지 여부를 나타낸 것으로 정의합니다.

위 그림은 $L[j-1]$과 $M[y_j=t]$으로 $L[j]$를 얻는 과정입니다. 편의상 $L$ 대신 $L^\prime$을 사용합니다. $L^\prime [j-1]$과 $L^\prime [j]$를 비교하면 0 비트가 오른쪽으로 이동하였음을 볼 수 있습니다. 단조성에 따라 $j-1$ 행보다 $j$ 행에서 DP 테이블의 값이 증가했기 때문입니다. 이제 어떤 규칙에 따라 0 비트가 이동하는지를 보겠습니다. 우선 $M[i]=0$일 때는 $DP[i][j]$는 $DP[i-1][j]$와 $DP[i][j-1]$에 의해 결정되고, $M[i]=1$인 다른 $i$의 영향을 받지 않는 이상 $L^\prime[j]_i$의 값은 $L^\prime[j-1]_i$가 됩니다. $M[i]=1$이면서 $L^\prime[j-1]_i=0$일 때는 $DP[i][j-1]=DP[i-1][j-1]+1=DP[i][j]$이고, 따라서 0의 위치에 영향을 주지 않습니다. $M[i]=1$이면서 $L^\prime[j-1]_i=1$일 때는 DP 테이블의 값이 증가하는 곳이 앞당겨지므로 0의 위치를 오른쪽으로 옮길 수 있게 되는데, 이는 0 바로 오른쪽에 연속된 1의 block 위에 있으면서 $M[i]=1$을 만족하는 가장 작은(=가장 오른쪽의) $i$의 위치로 이동하게 됩니다.
이러한 과정을 비트 연산으로 계산해봅시다. 먼저 $M[i]=1$이면서 $L^\prime[j-1]_i=1$인 비트만 남기기 위해 둘의 AND 연산을 적용합니다. 여기서 살아남은 1들 중 각 block에서 가장 오른쪽에 있는 것의 위치에 0을 옮겨야 합니다. AND 연산의 결과에 $L^\prime[j-1]$을 더하면 받아올림되면서 둘의 위치가 바뀌게 됩니다. 그러나 이렇게 하면 각 block에서 $M[i]=0$인 $i$의 비트가 모두 0으로 바뀌는 문제가 발생합니다. 이를 해결하기 위해 $M[i]=0$이면서 $L^\prime[j-1]_i=1$인 $i$의 비트를 모두 1로 바꾸면 됩니다. 정리하면 다음과 같습니다.
\[L^\prime[j]=(L^\prime[j-1]+(L^\prime[j-1] \And M))\vert (L^\prime[j-1]\& M^\prime)\]Hunt-Szymanski 알고리즘
지금까지 살펴본 알고리즘들은 $A$와 $B$에 있는 모든 문자들의 쌍을 비교하였습니다. 이 방법으로는 시간 복잡도를 $O(nm)$ 밑으로 낮출 수는 없습니다. 하지만 결국 답에 영향을 주는 부분은 $A[i]=B[j]$를 만족하는 $(i, j)$들(이하 match point)입니다. 여기에 집중하면 시간 복잡도가 match point의 개수$(r)$에 대한 식으로 나타나는 알고리즘을 얻을 수 있습니다. $aaa\dots aa$와 같은 worst case가 아닌 일상적인 문장에서는 각 문자가 비교적 고르게 분포하고, 따라서 match point의 개수가 $nm$보다 크게 작을 수 있습니다. 이런 경우에는 $O(n+r\log n)$ 정도의 시간복잡도와 $O(n+r)$의 공간복잡도를 갖는 Hunt-Szymanski 알고리즘(이하 HS 알고리즘)이 더 효율적일 수 있습니다.
모든 match point들의 쌍 $((i, j), (i^\prime, j^\prime))$에 대해 $i<i^\prime, j<j^\prime$일 때 둘 사이에 단방향 간선을 추가해서 DAG를 구성할 수 있습니다. LCS의 길이는 이 DAG 상에서 최장 경로의 길이와 같고, 역추적을 통해 LCS를 하나 구성할 수도 있습니다.
이 과정을 $O(n\log n)$ LIS와 비슷한 방법으로 빠르게 할 수 있습니다. Bitset을 이용한 DP 최적화에서 했던 관찰을 그대로 적용하면 됩니다. DP 테이블의 각 행에서 $k$가 처음 등장하는 인덱스(=bitset $L^\prime$에서 0이 등장하는 인덱스)를 기록한 $T[i][k]$를 정의합니다. 그러면 다음 점화식을 얻을 수 있습니다.
\[T[i][k]= \begin{cases} \text{smallest }j\text{ s.t. }x_i=y_i \text{ and }T[i-1][k-1]<j\leq T[i-1][k] \\ T[i-1][k] \text{ if no such }j\text{ exists} \end{cases}\]$A$에 등장하는 각 문자에 대해 $B$에서 어느 위치에 등장하는지를 match list에 저장합니다. $A$의 $i$번째 문자에 대한 match list의 모든 원소 $j$에 대해 반복하면서 이분탐색으로 $k$를 찾습니다. $j<T[i-1][k]$라면 값을 업데이트하면서 $T[i-1][k-1]$에 해당하는 match point와 연결하여 LCS 복원에 활용합니다. 여기서 match list를 내림차순으로 정렬하면 $T[i]$를 뒤에서부터 채울 수 있는데 $T[i]$가 아닌 $T[i-1]$에 채우더라도 이분탐색의 결과에는 영향을 주지 않게 됩니다. 따라서 match list를 내림차순으로 전처리한 다음 1차원의 $T$에 업데이트를 반복하는 방식으로 공간을 아낄 수 있습니다.
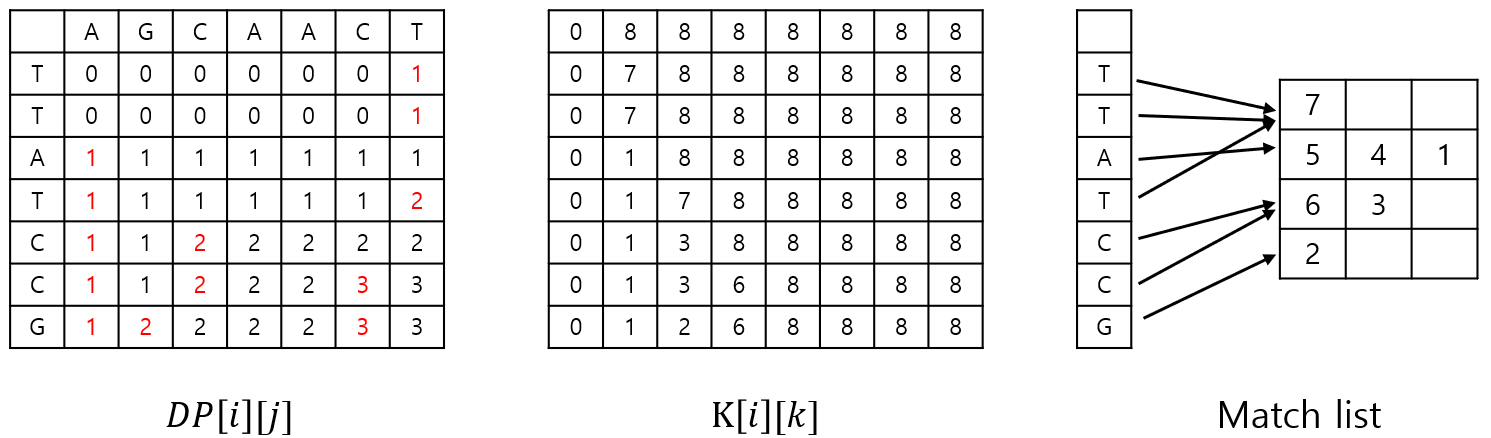
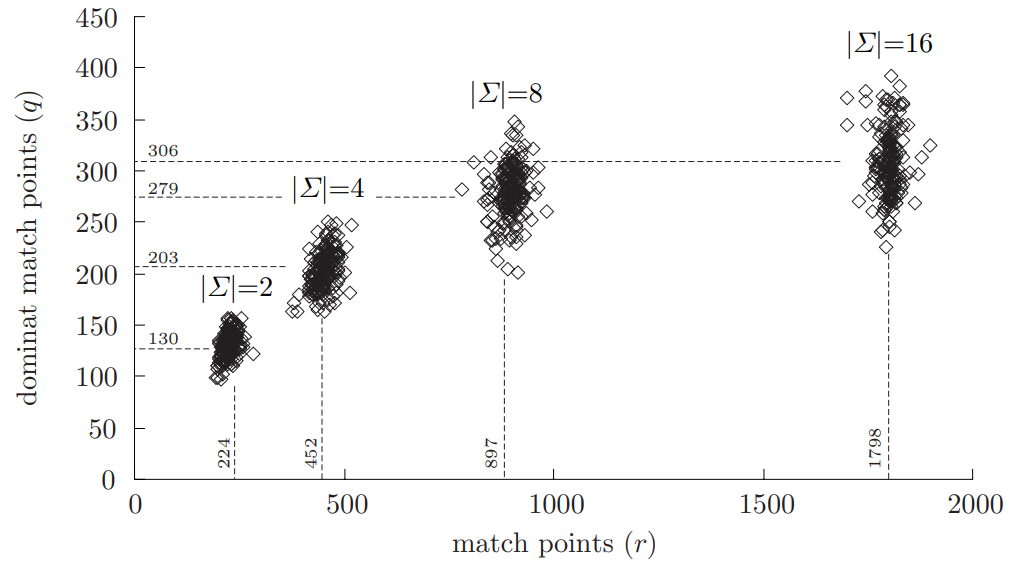
한편, $T$를 업데이트하는 match point들은 모두 dominant match point입니다. Dominant match point란 자신보다 $i$, $j$ 좌표가 둘 다 작거나 같으면서 DP 테이블 상의 값이 같은 match point가 없는 match point입니다. DP 테이블에서 같은 값들을 가진 값들을 보면 오른쪽으로 올라가는 계단 모양이 되는데, 여기서 튀어나온 부분이 dominant match point입니다. 계산에 실질적으로 영향을 주는 부분이 이것뿐이므로, match point들 중에 dominant match point들만 남기는 효율적인 방법이 있다면 연산을 크게 줄일 수 있습니다. 다음은 문자의 개수를 달리하였을 때 랜덤한 문자열에서 match point의 개수$(r)$와 dominant match point의 개수$(q)$를 나타낸 그래프입니다. 문자의 개수가 커질수록 $\frac{q}{r}$이 작아지므로 더 높은 최적화 효율을 얻을 수 있습니다.
Bitset을 이용한 최적화
고정된 match list를 쓰는 대신 set을 활용해 유동적인 match list를 사용하는 알고리즘이 있습니다. [3] 이 방법으로 insert, delete, lower_bound 등 연산의 횟수가 $O(q)$임이 보장되지만, set의 상수가 크기도 하고 한 번의 iteration에 여러 번의 set 연산이 필요하여 실제 성능을 보장하기 어렵다고 합니다.
이 문제를 해결하기 위해, 또다시 bitset을 이용한 최적화를 적용할 수 있습니다. 지금까지 관찰에 따르면 match point$(i, j)$가 dominant하다는 것과 다음 식은 동치입니다.
\[DP[i][j]=DP[i-1][j-1]+1=DP[i-1][j]+1=DP[i][j-1]\]이를 bit vector $L^\prime$으로 나타내면 $L^\prime [j-1]_i=1 \text{ and }L^\prime [j]_i=0$입니다. 그렇다면 $(L^\prime [j-1] \oplus L^\prime [j]) \And L^\prime [j-1]$의 결과에서 $i$번째 bit가 1이라면 $(i, j)$는 dominant match point입니다.
그러나 이것만으로는 기존 HS 알고리즘을 최적화하기 어렵습니다. 이렇게 얻은 dominant match point들을 정렬하는 작업이 추가로 필요하기 때문입니다. 이는 HS 알고리즘은 row-wise로 작동하는 반면 bit vector 연산은 column-wise로 작동하기에 생기는 문제입니다. 이 문제의 해결책으로, HS 알고리즘을 column-wise로 변형합니다. 매 column이 계산될 때마다 그때그때 dominant match point들을 찾고 이를 가지고 HS 알고리즘을 적용하면 됩니다.
결국 비트 연산을 하기 위해 DP 테이블 전체를 bit vector으로 계산하는 과정과 이를 바탕으로 dominant match point를 찾는 과정의 시간 복잡도가 $O(\frac{nm}{64})$입니다. 여기에 HS 알고리즘의 $O(r\log n)$이 추가됩니다. 하지만 이러한 과정으로 $O((r-q)\log n)$의 시간을 절약한다면 더 효율적일 수 있습니다. 마찬가지로 Hirschberg 알고리즘과 비교한다면, 이는 재귀를 사용하므로 상수가 큽니다. 개선된 HS 알고리즘은 $O(r\log n)$의 시간을 더 쓰는 대신 상수를 줄입니다.
참고문헌
[1] Crochemore, M., Iliopoulous, C. S., & Pinzon, Y. J. (2003). Speeding-up hirschberg and hunt-szymanski lcs algorithms. Fundamenta Informaticae, 56(1-2), 89-103.
[2] Crochemore, M., Iliopoulos, C. S., Pinzon, Y. J., & Reid, J. F. (2001). A fast and practical bit-vector algorithm for the longest common subsequence problem. Information Processing Letters, 80(6), 279-285.
[3] Apostolico, A. (1986). Improving the worst-case performance of the Hunt-Szymanski strategy for the longest common subsequence of two strings. Information Processing Letters, 23(2), 63-69.