Introduction
행렬 곱셈은 병렬 프로그래밍에서 가장 중요한 연산 중 하나입니다. 행렬 곱셈은 컴퓨터 그래픽스, 인공 신경망 등 다양한 분야에서 기본적인 연산으로 사용되며, 사용하는 메모리에 비해 연산의 수가 많아 병렬화하기에 적합하기 때문입니다.
GPU는 이러한 병렬 연산에 특화된 하드웨어입니다. GPU에는 단순한 연산 수천 개를 동시에 수행하도록 많은 연산 장치가 있으며 CPU의 cache 구조와 비슷하게 각 계층에서 공유되는 메모리가 있습니다.
행렬 곱셈을 위한 cuBLAS와 같은 라이브러리가 있으며, 이 글에서 소개할 내용은 해당 라이브러리를 구현하는 데 사용된 테크닉의 일부입니다. 이들은 GPU의 하드웨어 특성을 최대한 활용하는 것을 목표로 합니다.
(이 글은 https://siboehm.com/articles/22/CUDA-MMM 등을 기반으로 작성되었습니다.)
Tiling
CUDA 커널이 실행되면 하나의 Grid가 생성됩니다. 이 Grid는 3차원 인덱스를 갖는 block으로 이루어져 있습니다. 각 block은 마찬가지로 3차원 인덱스를 찾는 thread으로 이루어져 있습니다. 여기서 각 thread들은 병렬적으로 연산을 수행하게 됩니다. block과 thread의 인덱스는 계산할 부분을 나누는 데 중요한 정보가 됩니다.
GPU에는 어느 block에서나 접근 가능한 Global memory, 각 block에서 공유되는, Shared memory, 각 thread 내부에서 사용할 수 있는 register가 있습니다. 접근 속도는 register, Shared memory, Global memory 순으로 빠릅니다.
GPU와 CUDA의 계층적 구조를 활용하면 행렬 곱셈의 성능을 향상할 수 있습니다. 행렬을 tile들로 분할해서 이를 각 계층에 적절히 할당하는 방법을 알아보겠습니다.
구현 예시 코드는 $B$가 transpose되어 있음을 가정합니다. 즉 $AB^T=C$를 계산하는 코드입니다.
Naive implementation
행렬 곱셈 $AB=C$는 다음과 같이 3중 반복문으로 계산할 수 있습니다.
for(int i=0; i<H; i++){
for(int j=0; j<W; j++){
for(int k=0; k<K; k++) C[i][j]+=A[i][k]*B[k][j];
}
}
가장 간단하게 이 코드를 병렬화하는 방법은, 하나의 thread가 $C$의 원소 하나를 계산하도록 만드는 것입니다. $C$를 2차원 block으로 분할하는 구조의 커널은 다음과 같이 호출할 수 있습니다.
dim3 DimGrid=(W+BlockSize-1)/BlockSize, (H+BlockSize-1)/BlockSize, 1);
dim3 DimBlock=(BlockSize, BlockSize, 1);
matmul<<<DimGrid, DimBlock>>>(A, B, C, ...);
다음은 matmul 커널을 구현하는 방법입니다. Dim, Idx 변수를 이용해 해당 thread가 담당하는 $C$의 인덱스를 계산합니다.
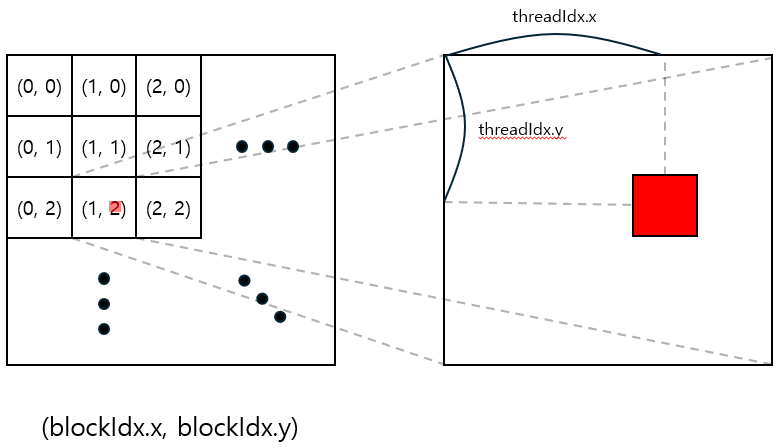
이제제 가장 안쪽 반복문을 실행하여 계산한 인덱스에 해당하는 $C$의 값을 계산하면 됩니다. $C$에 반복적으로 접근하는 대신, 임시 변수를 만들어 합을 구한 다음 최종 결과만 저장하는 것이 좋습니다.
> 클릭하여 코드 보기
__global__ void matmul1(const float *A, const float *B, float *C, int H, int W, int K){
int row=threadIdx.y+blockIdx.y*blockDim.y;
int col=threadIdx.x+blockIdx.x*blockDim.x;
float sum=0.0f;
if(row<H && col<W){
for(int k=0; k<K; k++) sum+=A[row*K+k]*B[col*K+k];
C[row*W+col]+=sum;
}
}
Using shared memory
행렬 곱셈 연산에서 $A$, $B$의 각 원소는 각각 $W$, $H$번 load됩니다. 행렬 곱셈 알고리즘 자체를 바꾸지 않는 한 load의 수 자체를 줄일 수는 없지만, GPU의 메모리 구조를 이용하면 실행속도를 크게 향상시킬 수 있습니다.
같은 block 안의 thread들은 $C$에서 직사각형 모양 tile을 담당합니다. 이 tile 안에는 행 또는 열의 인덱스가 서로 겹치는 원소들이 모여 있습니다. 그러므로 하나의 block 안에서 $A$, $B$의 같은 원소를 여러 번 참조하게 됩니다. 같은 block끼리 공유하는 Shared memory를 사용합니다. Global memory에 여러 번 접근하는 대신, Global memory에는 한 번만 접근하고 Shared memory에 같은 횟수만큼 접근하는 것이 더 효율적입니다.
이 커널은 두 단계로 동작합니다. 첫 번째로 $A$와 $B$의 일부를 Shared memory에 저장합니다. 각 thread들은 $A$, $B$의 값을 load해서 Shared memory에 저장하게 됩니다. Shared memory 용량은 제한적이기 때문에, $C$를 계산하는 데 필요한 모든 값들을 한 번에 저장할 수는 없고, 일정한 개수만큼 끊어서 저장합니다.
두 번째로는 Shared memory에 저장된 값을 참조하여 $C$를 계산하면 됩니다. Shared memory에 저장된 부분까지 계산하면 되고, 완료되었다면 다시 첫 번째 단계로 돌아가 다음 부분을 Shared memory에 저장하면 됩니다. 이를 계산이 완료될 때까지 반복합니다.
Shared memory에 모든 값이 저장되기 전에 계산이 시작되거나, 계산이 완료되기 전에 Shared memory의 값이 바뀌게 된다면 잘못된 계산값을 얻게 됩니다. 그러므로 모든 thread에서 각 단계가 완료되었을 때만 다음 단계로 넘어갈 수 있도록 __syncthreads() 함수를 사용해야 합니다.
Shared memory 배열의 크기를 block의 크기와 같게 설정한다면 하나의 thread가 하나의 $A$, $B$ 원소에 각각 접근하고 값을 가져오면 됩니다. block 내부의 threadIdx 변수를 이용해 $A$, $B$에서 가져올 원소의 인덱스를 계산하고 이를 Shared memory에 저장하면 됩니다.
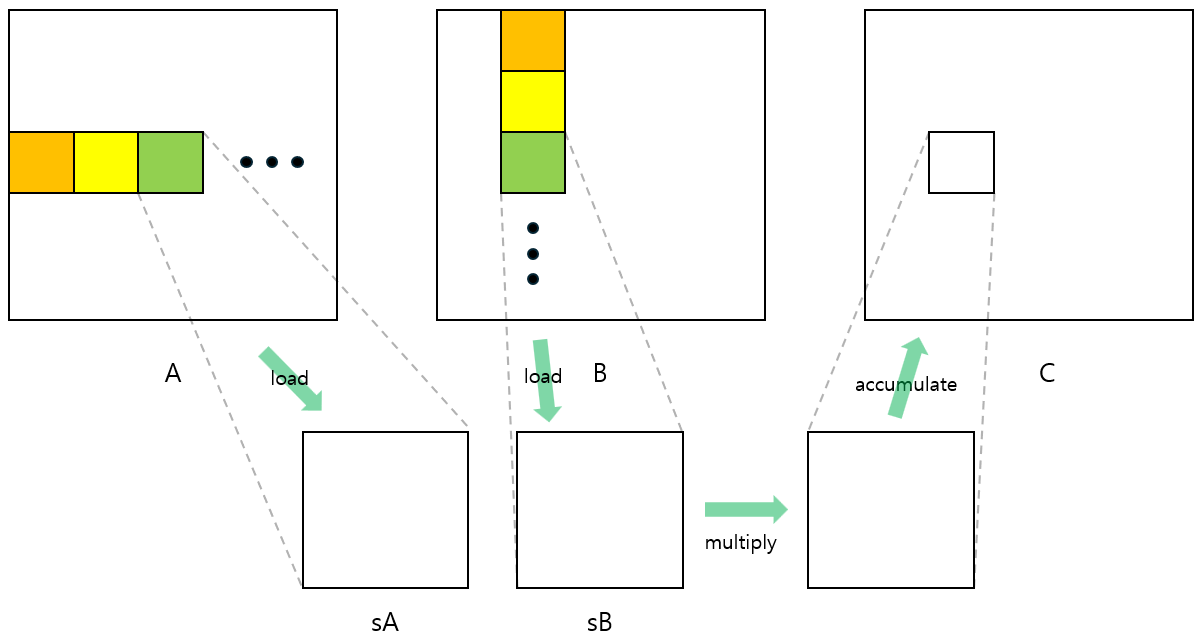
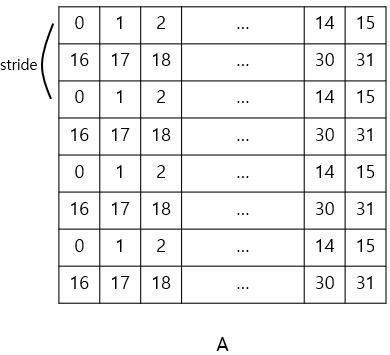
여기서 중요한 부분은 memory coalescing입니다. 하나의 warp에 포함된 32개의 thread들은 같은 명령어를 동시에 수행합니다. 그리고 GPU의 cache line은 128B(=float 32개)입니다. 그러므로 32개의 thread들이 하나의 cache line 위에서 load를 수행한다면 한 번의 메모리 접근으로 한 warp의 모든 load 명령어를 수행할 수 있습니다.
다음과 같이 계산된 인덱스 순서대로 Global memory의 연속된 원소를 load하면 됩니다.
int thread_id=threadIdx.z*(blockDim.y*blockDim.x)+threadIdx.y*blockDim.x+threadIdx.x;
> 클릭하여 코드 보기
__global__ void matmul2(const float *A, const float *B, float *C, int H, int W, int K){
__shared__ float sA[TILESZ][TILESZ];
__shared__ float sB[TILESZ][TILESZ];
int row=threadIdx.y+blockIdx.y*blockDim.y;
int col=threadIdx.x+blockIdx.x*blockDim.x;
int r=threadIdx.y;
int c=threadIdx.x;
float sum=0.0f;
for(int i=0; i<(K+TILESZ-1)/TILESZ; i++){
if(row<H && (i*TILESZ+c)<w) sA[r][c]=A[row*w+i*TILESZ+c]; // coalesced
else sA[r][c]=0.0f;
if(col<W && (i*TILESZ+r)<w) sB[c][r]=B[col*w+i*TILESZ+r]; // not coalesced
else sB[c][r]=0.0f;
__syncthreads();
for(int k=0; k<TILESZ; k++) sum+=sA[r][k]*sB[c][k];
__syncthreads();
}
if(row<H && col<W) C[row*W+col]+=sum;
}
Using registers
지금까지는 한 thread가 $C$의 원소 하나만을 담당했습니다. 하나의 thread가 여러 개의 원소를 계산하도록 한다면 thread 안에서 사용할 수 있는 더욱 빠른 메모리인 register을 활용할 수 있습니다.
구현 방식은 이전 커널과 비슷합니다. 여기에 Shared memory에 저장된 값을 register로 옮기는 과정만 추가하면 됩니다. 그런데 이번에는 shared memory 배열의 크기가 thread의 개수보다 큽니다. 그러므로 threadIdx를 가지고 $C$에 대응되는 인덱스 이외에도 $A$, $B$에 대응되는 인덱스도 계산해야 합니다. 이렇게 계산된 인덱스에 있는 $A$, $B$의 값을 Shared memory에 저장하면 됩니다.
이후에는 Shared memory에 저장된 값의 일부를 크기가 작은 배열로 가져오면 됩니다. 크기가 4인 배열로 값을 가져온다면, Shared memory로의 4번 접근을 Shared memory 1번과 register 4번 접근으로 바꿀 수 있으므로 메모리 접근 시간을 줄이게 됩니다.
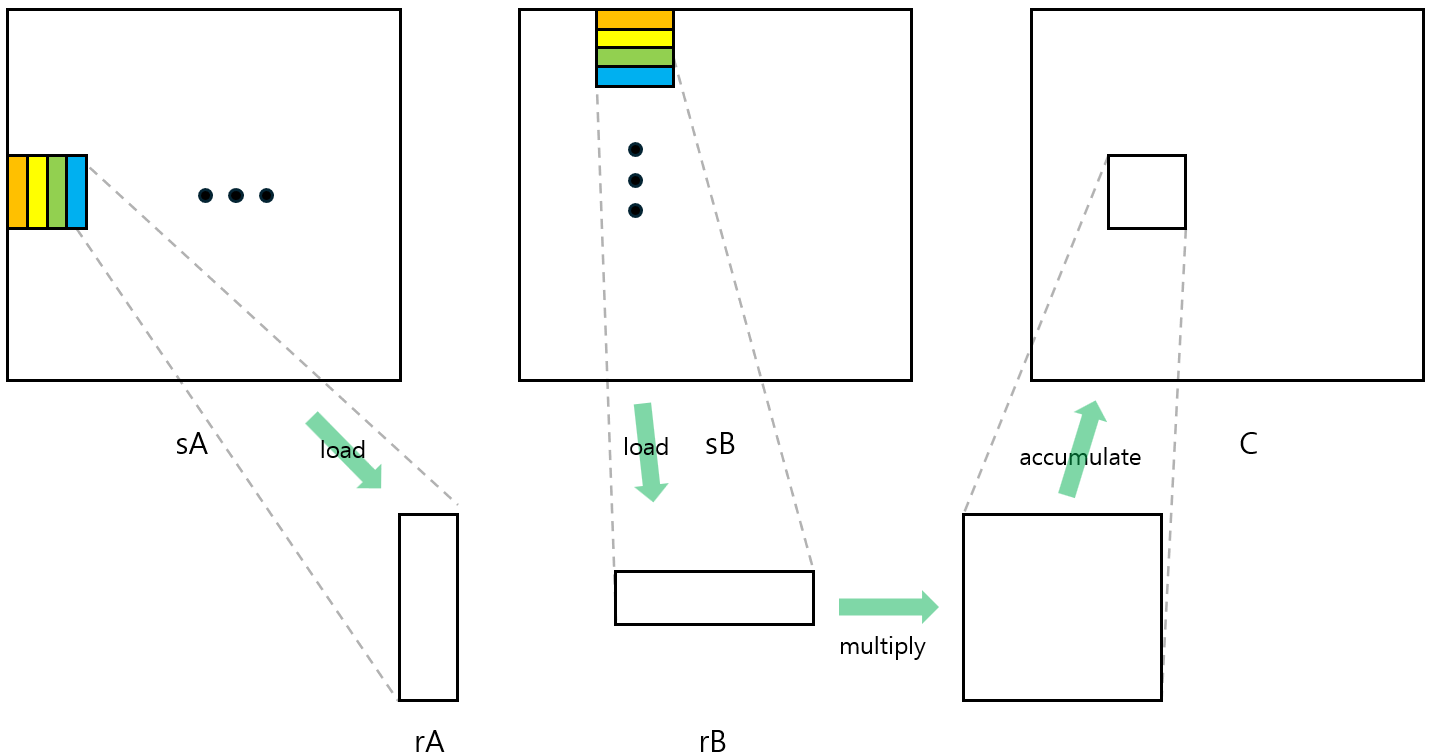
> 클릭하여 코드 보기
__global__ void matmul3(const float *A, const float *B, float *C, int H, int W, int K){
__shared__ float sA[TILESZ*4][WID];
__shared__ float sB[TILESZ*4][WID];
int row=threadIdx.y+blockIdx.y*blockDim.y;
int col=threadIdx.x+blockIdx.x*blockDim.x;
int r=threadIdx.y;
int c=threadIdx.x;
float sum[4*4]={0.0f};
float rA[4]={0.0f};
float rB[4]={0.0f};
A+=blockIdx.y*blockDim.y*K*4;
B+=blockIdx.x*blockDim.x*K*4;
int SZ=WID;
int stride=(TILESZ*TILESZ)/SZ;
for(int i=0; i<(K+SZ-1)/SZ; i++){
int idx=r*TILESZ+c;
int xx=idx/SZ;
int yy=idx%SZ;
for(int j=0; j<SZ; j+=stride){
if(row<H && (i*SZ+yy)<K) sA[xx][yy]=A[xx*K+yy];
else sA[xx][yy]=0.0f;
xx+=stride;
}
xx=idx/SZ;
for(int j=0; j<SZ; j+=stride){
if(col<W && (i*SZ+yy)<K) sB[xx][yy]=B[xx*K+yy];
else sB[xx][yy]=0.0f;
xx+=stride;
}
A+=SZ;
B+=SZ;
__syncthreads();
for(int i=0; i<SZ; i++){
for(int j=0; j<4; j++) rA[j]=sA[4*r+j][i];
for(int j=0; j<4; j++) rB[j]=sB[4*c+j][i];
for(int j=0; j<4; j++){
for(int k=0; k<4; k++) sum[j*4+k]+=rA[j]*rB[k];
}
}
__syncthreads();
}
if(row*4<H && col*4<W) {
for(int i=0; i<4; i++){
int ix=(row*4+i)*W+col*4;
for(int j=0; j<4; j++){
C[ix]+=sum[i*4+j];
ix++;
}
}
}
}
Other techniques
Vectorized load & store
float형 대신 float4를 활용하면 한 번에 여러 개의 float를 Shared memory나 register에 불러올 수 있습니다. 이때 인덱스 계산 방법을 float4에 맞게 조금 바꾸면 됩니다.
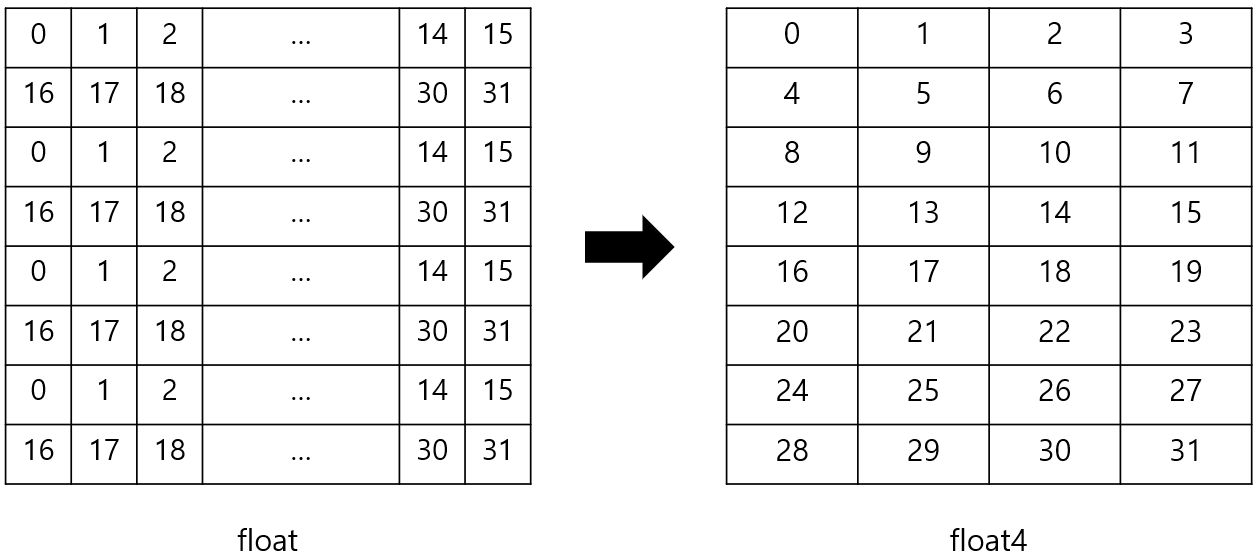
float를 float4 형식으로 불러오기 위해서는 type cast가 필요합니다. reinterpret_cast를 이용하면 됩니다.
Shared memory에서 register으로 불러올 때도 vectorization을 사용하기 위해서는 필요에 따라 Shared memory를 transpose해야 합니다. Global memory에서 가져온 값을 float4 형식 변수에 저장하고, 4개의 float 값을 transpose된 위치에 각각 넣으면 됩니다. 다음은 register blocking과 vectorization을 적용한 코드입니다.
> 클릭하여 코드 보기
__global__ void matmul4(float *A, float *B, float *C, int H, int W, int K){
const int SZ=16;
__shared__ float sA[SZ][TILESZ*BTSZ];
__shared__ float sB[SZ][TILESZ*BTSZ];
int row=threadIdx.y+blockIdx.y*blockDim.y;
int col=threadIdx.x+blockIdx.x*blockDim.x;
int r=threadIdx.y;
int c=threadIdx.x;
float sum[BTSZ*BTSZ]={0.0f};
float rA[BTSZ];
float rB[BTSZ];
A+=blockIdx.y*blockDim.y*K*BTSZ;
B+=blockIdx.x*blockDim.x*K*BTSZ;
int stride=(TILESZ*TILESZ*4)/SZ;
for(int i=0; i<(K+SZ-1)/SZ; i++){
int idx=r*TILESZ+c;
int xx=idx/(SZ/4);
int yy=idx%(SZ/4);
for(int j=0; j<TILESZ*BTSZ; j+=stride){
float4 tmp=reinterpret_cast<float4 *>(&A[xx*K+yy*4])[0];
sA[yy*4][xx]=tmp.x;
sA[yy*4+1][xx]=tmp.y;
sA[yy*4+2][xx]=tmp.z;
sA[yy*4+3][xx]=tmp.w;
xx+=stride;
}
xx=idx/(SZ/4);
for(int j=0; j<TILESZ*BTSZ; j+=stride){
float4 tmp=reinterpret_cast<float4 *>(&B[xx*K+yy*4])[0];
sB[yy*4][xx]=tmp.x;
sB[yy*4+1][xx]=tmp.y;
sB[yy*4+2][xx]=tmp.z;
sB[yy*4+3][xx]=tmp.w;
xx+=stride;
}
A+=SZ;
B+=SZ;
__syncthreads();
for(int i=0; i<SZ; i++){
reinterpret_cast<float4 *>(rA)[0]=reinterpret_cast<float4 *>(&sA[i][BTSZ*r])[0];
reinterpret_cast<float4 *>(rB)[0]=reinterpret_cast<float4 *>(&sB[i][BTSZ*c])[0];
for(int j=0; j<BTSZ; j++){
float tmp=rA[j];
for(int k=0; k<BTSZ; k++) sum[j*BTSZ+k]+=tmp*rB[k];
}
}
__syncthreads();
}
if(row*BTSZ<H && col*BTSZ<W) {
for(int i=0; i<4; i++){
float4 tmp=reinterpret_cast<float4 *>(&C[(row*4+i)*W+col*4])[0];
tmp.x+=sum[i*4+0];
tmp.y+=sum[i*4+1];
tmp.z+=sum[i*4+2];
tmp.w+=sum[i*4+3];
reinterpret_cast<float4 *>(&C[(row*4+i)*W+col*4])[0]=tmp;
}
}
}
Pre-fetching
지금까지 구현한 kernel들은 Shared memory에 값을 저장하는 단계와 그 값을 이용해 행렬곱을 계산하는 두 단계로 나누어져 있습니다. 그리고 메모리의 값을 변경하는 것은 계산 결과에 영향을 주기 때문에 각 단계가 마무리될 때까지 thread를 대기시켜야 합니다.
두 단계를 한 번에 진행시키더라도 메모리에 영향을 주지 않게 한다면 __syncthread() 함수 실행 횟수를 줄일 수 있습니다. Shared memory 배열을 2개로 만든다면 이전 반복문에서 저장된 값들을 참조하여 행렬 곱셈을 계산하는 동시에 다른 배열에 Global memory의 값을 저장할 수 있습니다. 이 방법으로 __syncthreads() 함수 호출을 반복문 당 2번에서 1번으로 줄일 수 있고 thread가 연산을 수행하지 않고 대기하는 시간을 줄일 수 있습니다.
다만 Shared memory를 2배로 사용하게 되고 Multiprocessor 당 Shared memory 크기의 제한이 있습니다. 그러므로 활성화된 thread의 수는 절반까지 줄어들 수 있습니다. 그러므로 이 방식은 Shared memory가 아닌 다른 자원에 의해 실행 속도에 병목현상이 생겼을 때 활용할 수 있습니다.
> 클릭하여 코드 보기
__shared__ float sA[2][];
__shared__ float sB[2][];
__global__ void matmul(const float *A, const float *B, float *C, int H, int W, int K){
// load tile to sA[0][], sB[0][]
int numTiles=(K+TILESZ-1)/TILESZ
for(int i=0; i<numTiles; i++){
__syncthreads();
if(i!=numTiles-1){
// load tile to sA[(i+1)%2][], sB[(i+1)%2][]
}
// compute matmul using sA[i%2][], sB[i%2][]
}
}
Tuning parameters
block의 크기, Shared memory 배열의 크기 등 parameter을 조절하는 것도 성능에 큰 영향을 미칩니다. GPU에는 사용할 수 있는 thread의 수, Shared memory의 용량 등 자원이 한정되어 있고 parameter에 따라서 어떤 제한에 걸리게 되는지가 달라집니다. 다음은 GeForce RTX 3090의 스펙입니다.
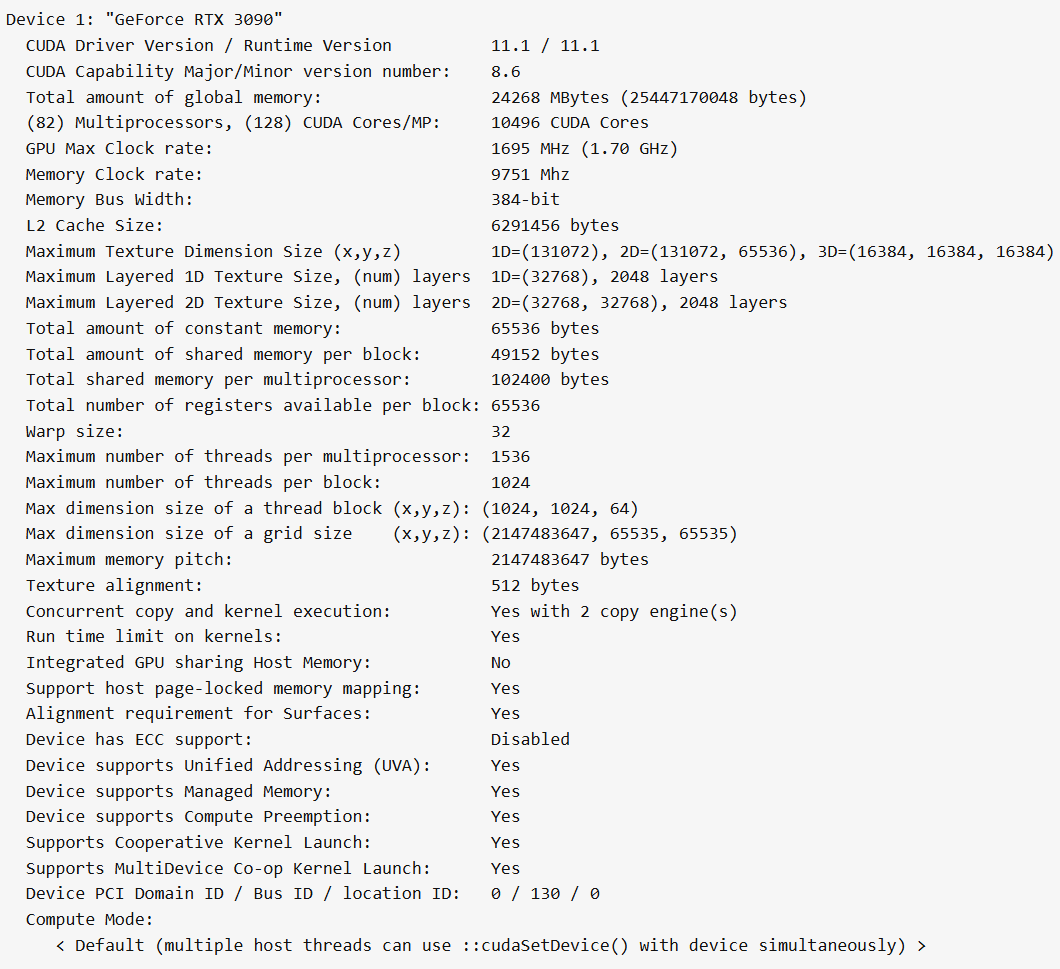
예를 들어서 matmul2 커널에서 TILESZ=32일 때, 한 block에서 실행되는 thread는 1024개입니다. 2개의 block이 동시에 실행된다면 총 thread는 2048개이므로 multiprocessor당 thread 개수 제한에 걸리게 됩니다. 그러므로 1개의 block만이 실행 가능하며 활성화되는 thread의 수는 1024개입니다. TILESZ=16일 때는 한 block당 thread는 256개이므로 총 6개의 block이 동시에 실행되고, 활성화되는 thread의 수는 1536개입니다. TILESZ가 32일 때보다 16일 때 더 많은 thread를 동시에 사용할 수 있습니다.
이번에는 matmul3 커널에서 32x32의 배열 sA, sB를 사용한다고 가정합시다. 그러면 block당 thread는 총 64개이고 Shared memory 사용량은 8kB입니다. multiprocessor 당 동시에 처리 가능한 block의 개수는 thread 수 제한 기준으로 $\frac{1536}{64}=24$개, Shared memory 용량 기준으로 $\frac{96}{8}=12$개입니다. Shared memory 기준에 먼저 걸리게 되므로 한 번에 12개의 block이 처리되며 활성 thread는 768개입니다. 여기서 sA, sB의 가로 길이를 16으로 줄이면 thread 개수는 그대로지만 Shared memory 사용량은 절반이 되므로 동시에 처리되는 block과 thread의 개수는 2배가 되어 1536개가 됩니다.
그러나 Shared memory의 가로 길이를 줄이는 것은 coalescing 관점에서 불리하기 때문에 원하는 만큼의 성능 향상을 얻지 못할 수 있습니다. 이렇게 특정 제한을 피해서 parameter을 조정하더라도 다른 곳에서 성능이 제한될 수 있습니다. 또한 계산할 행렬의 크기에 따라서도 최적의 parameter는 달라집니다. 그러므로 최적의 parameter를 계산하는 것은 어렵고, parameter의 여러 조합들을 직접 실행해 보는 방식으로 최적값을 결정합니다.
Conclusion
이번 글에서 GPU를 이용한 행렬 곱셈 최적화 방법을 단계별로 알아보고 독립적으로 사용할 수 있는 몇 가지 테크닉까지 알아보았습니다.
각 테크닉을 적용하면서 행렬 곱셈의 성능이 점점 향상됨을 관찰하였습니다. 그러나 성능 최적화에는 여러 요소가 있기 때문에, 어떤 테크닉을 적용하더라도 성능이 이전과 비슷하거나 오히려 저하되는 것도 관찰하였습니다. parameter의 조합을 고르듯이 성능에 유리한 테크닉의 조합을 고르는 것이 가장 빠른 커널을 구현하는 방법이라는 생각이 듭니다.
다음 글에서는 단계별 과정의 다음 단계인 Warptiling과 tensor core 사용 등을 다뤄보려고 합니다.
참고문헌
[1] https://siboehm.com/articles/22/CUDA-MMM
[2] https://cnugteren.github.io/tutorial/pages/page12.html
[3] https://leimao.github.io/article/CUDA-Matrix-Multiplication-Optimization/
[4] https://developer.nvidia.com/blog/cutlass-linear-algebra-cuda/