Markov Chain Monte Carlo 샘플링의 마법
이번 포스트에서는 강력한 샘플링 기법 중 하나인 Markov Chain Monte Carlo(MCMC)에 대해 알아보겠습니다. MCMC의 활용도는 굉장히 넓어서 머신러닝을 비롯한 베이지안 통계학, 통계물리학, 컴퓨터비전, 자연어처리 등의 분야에 널리 쓰이고 있습니다. 하지만 MCMC는 역사가 짧고 (1990년대에 들어서 영향력을 발휘하기 시작) MCMC를 설명한 대부분의 자료가 수학적인 언어로만 쓰여진 탓에, 아직까지 개발자들에게 읽고 적용하기 좋은 가이드가 부족한 상태입니다. 특히나 한글 자료는 많이 부족합니다. 따라서 국내 개발자들도 MCMC를 이해하고 실제로 사용할 수 있도록 알고리즘을 체득하면 좋겠다고 생각해서 이 글을 작성하게 되었습니다. 부족하지만 도움이 되었으면 좋겠습니다.
목차
- 샘플링이란?
- 샘플링이 어려운 이유
- 샘플링이 필요한 이유
- MCMC의 개념과 수학적 원리
- Markov Chain
- MCMC 속 Markov Chain
- Metropolis-Hastings 알고리즘을 익혀보자
- 말로 풀어쓴 Metropolis-Hastings 알고리즘
- 장점, 단점 및 구현
- 참고문헌
샘플링이란?
우리에게 가장 익숙한 샘플링의 의미는 단연코 “배열에서 랜덤하게 원소를 뽑는 작업”일 것입니다. 심지어 대부분의 언어가 sample 또는 random_sample이란 이름의 라이브러리 함수를 제공하고 있어서 한 줄의 코드로 샘플링 작업을 할 수 있지요. 하지만 통계학에서 사용하는 조금 더 넓은 의미의 샘플링은 “임의의 확률 분포 $p(x)$로부터 표본을 추출하는 작업“입니다. 주사위로 예를 들어 보겠습니다. 우리가 주사위를 여러번 던질 때, 매번 도출된 앞면의 숫자가 표본입니다. 이 때 확률 분포는 각 주사위의 숫자가 도출 될 상대적인 확률을 의미하는 값이므로 $p(1)=p(2)=\cdots=p(6)= {1\over6}$ 이 됩니다.
주사위는 상태가 1부터 6까지로 매우 적지만, 상태 개수가 매우 많거나 아예 연속적인 분포도 있습니다. 그러한 확률 분포로부터 샘플링을 하는 것은 때때로 쉬운 경우도 있으나 대부분은 매우 어려운 문제입니다. 아무리 계산을 잘하는 컴퓨터라도 기존의 방법으로는 처리하지 못하는 범위라는게 존재하니까요.
샘플링이 어려운 이유
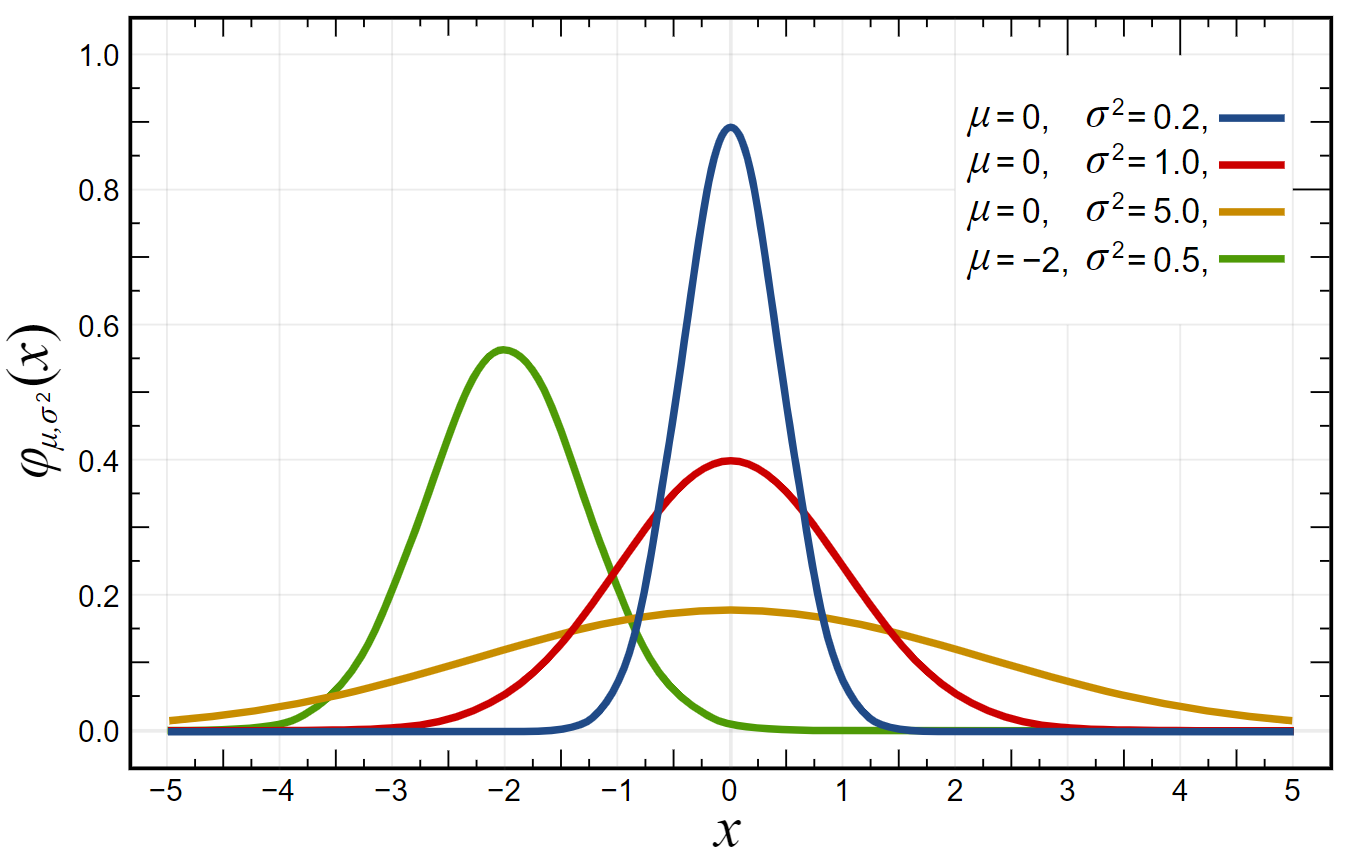
샘플링이 non-trivial한 가장 간단한 예시는 바로 정규분포입니다. 이 분포는 $-\infty$ 부터 $\infty$ 까지 연속적인 상태를 가지기 때문에 단순히 배열로 처리할 수는 없습니다. 가장 간단한 방법은 적절히 범위를 정해놓고 구간을 $N$개로 쪼갠 다음에 각 구간의 중심값으로만 샘플링 하는 것입니다. 하지만 이 방법은 상태 갯수가 N개로 고정되어 버리는 치명적인 단점이 있고, 또 양 끝쪽의 샘플을 정확하게 얻을 수가 없습니다. 만약에 이 정도의 오차를 허용하더라도 정규분포가 아닌 더 복잡한 모양의 분포, 특히 작은 구간에서 요동치는 분포의 경우에는 같은 방법을 적용할 수 없습니다. 짧지만 확실한 변화를 캐치할 수 없으니까요. 정확하고 빠르게 샘플링을 하려면 다른 방법을 생각해야 합니다.
다행히도 정규분포와 같은 일부 “좋은 형태”의 분포들은 상수 시간으로 쉽게 샘플링을 할 수 있는 방법이 개발되었습니다. 하지만 아직까지 일반적으로 모든 확률 분포에 적용할 수 있는 매우 빠른 샘플링 기법은 개발되지 않은 상태입니다.
좀 더 철학적으로 접근해 봅시다. 만약 샘플링이 쉬운 문제라면, 즉 임의의 확률 분포로부터 빠르게 샘플링이 가능하다면 무슨 일이 일어날까요? 바로 우리는 NP-Hard 최적화 문제를 빠르게 풀 수 있게 됩니다. 임의의 함수 $f(x)$의 global optimum을 찾는 최적화 문제를 푼다고 할 때, 임의의 상수 $K$에 대해 $e^{Kf(x)}$에 비례하는 확률 분포 $p(x)$가 존재하고 저희는 이 확률분포 $p(x)$로부터 샘플을 쉽게 얻을 수 있습니다. 만약 $K$에 큰 값을 부여한다면, $f(x)$의 값이 높은 $x$일 수록 상대적으로 도출 빈도가 매우 높아질 것입니다. 따라서 $K$를 무한대에 가깝게 설정하면, 결국 쉽게 얻어진 샘플들은 global optimum으로 수렴하게 됩니다. 또한 $x$를 subset으로 $f$를 subset에 속한 원소의 합으로 치환하면, 그 유명한 Subset sum problem이 됩니다.
샘플링이 필요한 이유
따라서 샘플링은 기본적으로 어렵습니다. 하지만 그럼에도 불구하고 샘플링은 꼭 필요합니다. 샘플링이 필요한 경우는 근본적으로 2가지입니다. 첫번째는 높은 차원의 최적화 문제를 풀 때, 두번째는 높은 차원의 적분을 할 때 입니다. 여기서 높은 차원이란, 말 그대로 높은 차원의 실수 공간을 말하기도 하고 때로는 컴퓨터가 처리하기에 상태개수가 너무 많은 경우를 말하기도 합니다.
Subset sum problem이 어려운 이유가 선택가능한 부분집합의 개수가 너무 많아서, 즉 $2^N$개로 높은 차원이기 때문입니다. 하지만 만약 위에서 정의한 확률분포에 대해 샘플링이 가능하다면, 그 많은 상태를 다 보지 않고도 선택적 표본을 통해 이 최적화 문제를 푸는게 가능하겠죠. 물론 이 문제를 샘플링으로 다항시간내에 해결한 것은 아니지만, 유사한 방법으로 다른 높은 차원의 non-trivial한 최적화 문제를 샘플링을 풀 수 있을지 모릅니다.
어떤 함수 $f(x)$를 계산할 수 있고 확률분포 $p(x)$를 샘플링 할 수 있을 때, 우리는 다음 형태의 적분을 아주 효과적으로 풀수 있습니다.
$\int f(x)p(x) dx$
심지어 $p(x)$를 계산하지 못하더라도 샘플링만 할 수 있으면 됩니다. 위 적분은 다음과 같이 근사시킬 수 있습니다.
$\int f(x)p(x) dx \approx \sum_{i=1}^{N} {f\left(X_i\right) \over N} $
여기서 $X_i$들은 $i$번째 표본 값이고 총 $N$개의 표본을 추출 했다는 뜻입니다. 왜 오른쪽 항에는 $p(x)$가 없을까요? 조금만 생각해보면 답을 쉽게 찾을 수 있습니다. 그 이유는 표본은 확률분포를 반영하므로, 전체 표본에서 각 상태의 출현 횟수는 자신의 확률분포 값에 비례하게 됩니다. 즉, $X_i$가 표본이기 때문에, 샘플이기 때문에 $p(x)$를 곱한 것과 같은 효과가 나타나는 것입니다. $N$이 점점 커질 수록 대수의 법칙에 의해 각 표본의 출현 횟수는 점점 정확한 확률 분포에 수렴하게 되고 결국은 정확한 적분 값에 도달하게 됩니다. 물론 수렴속도가 너무 느리면 안되지만요.
놀랍지 않나요? 대학교 1학년 미적분학 시간때 배우는 리만 합도 적분을 근사하지만 높은 차원에서는 불가능합니다. 결국 전체 공간을 다량의 미세한 구간으로 쪼개서 계산하는 것인데, 상태 개수가 많아지면 너무 오래 걸리니까요. 하지만 샘플링은 높은 차원에서도 적분을 가능하게 합니다. Wolframalpha는 적분값을 어떻게 구하고 있을지 한번 상상해봅시다.
이러한 적분 테크닉 덕분에 MCMC와 같은 샘플링 기법들이 머신러닝, 베이지안 통계학, 전산생물학 등에 쓰일 수 있는 것입니다. 언급하지는 않았지만 샘플링의 기본적인 속성인 simulation 덕분에 통계물리학에서도 널리 사용되고 있습니다.
MCMC의 개념과 수학적 원리
MCMC가 무엇인지 설명하기 전에 다른 샘플링 기법들에 비교하여 어떠한 점이 특별한지 먼저 언급하겠습니다. 앞에서 샘플링이 효과를 보려면 수렴속도가 느리면 안된다고 했습니다. 상태가 많은 문제, 즉 높은 차원의 문제를 풀기 위함인데 수렴속도가 느려버리면 의미가 없으니까요. 그렇습니다. MCMC가 각광받는 이유 중 첫번째는 빠른 수렴속도입니다. 절대적으로 빠르다고 단언할 수는 없지만 다른 샘플링 기법에 비해 상당히 빠르고 실용적으로 사용이 가능합니다. 두번째는 더 많은 확률분포를 샘플링 할 수 있습니다. Rejection sampling, Importance sampling과 같은 다른 기법들은 많은 형태의 분포를 다루지 못합니다.
이제 MCMC가 무엇인지 자세히 알아보겠습니다. MCMC는 샘플링을 하는 일종의 패러다임 입니다. 이름에서도 알 수 있듯이 Markov Chain과 Monte Carlo라는 두가지 수학적 특성을 기반으로 샘플링을 하는 것입니다. 즉, 특정한 알고리즘을 지칭하는 말은 아닙니다. MCMC의 샘플링 방법은 이전의 샘플이 다음 샘플의 추출에 영향을 줍니다. 정확히 표현하면 MCMC는 임의의 랜덤한 표본에서 시작하여, $i$번째 표본을 참고하여 $i+1$번째 표본을 뽑습니다. 엄청나게 큰 영역에서 어떤 부분은 적게 뽑고 어떤 부분은 많이 뽑아야 하는데, 아무것도 참고를 안하면 안되니까요.
MCMC가 놀라운 점은 겨우 바로 전 표본만을 이용하는데도, 표본을 100개, 1000개, … , 필요한 만큼 많이 뽑게 되면 현재까지 뽑은 전체 표본이 확률 분포를 거의 정확히 모방한다는 점입니다. 이 놀라운 효과를 보장하기 위해 Markov Chain을 사용합니다.
Markov Chain
Markov Chain은 부루마블 이나 모두의마블 아니면 모노폴리 같은 보드게임을 생각하면 이해하기 쉽습니다. 이와 같은 보드게임들은 여러개의 장소가 있고 주사위를 굴려서 나온 수 만큼 다른 장소로 이동하게 됩니다. 주목할 점은 각 장소에서 다른 장소로 이동할 수 있는 특별한 확률이 존재한다는 것인데요, 만약 주사위를 2개 굴린다면 앞으로 2칸 부터 12칸 까지 이동할 수 있는데 각각의 확률이 다 다릅니다. 행여나 찬스카드나 벌칙에 걸려서 다른 장소로 이동하게 되는 경우도 있습니다. 이 모든 경우를 생각하면 장소들을 node로, 각 장소에서 다른 장소로 이동하게 될 확률을 directed edge로 표현하여 보드의 모양을 directed graph로 만들 수 있습니다. 즉, 특정한 플레이어가 매턴 마다 보드위에서 주사위를 굴리며 다른 장소로 이동하는 것은, 이 그래프 위에서 매 턴마다 정해진 확률에 따라 다른 노드로 이동하는 것과 같습니다.
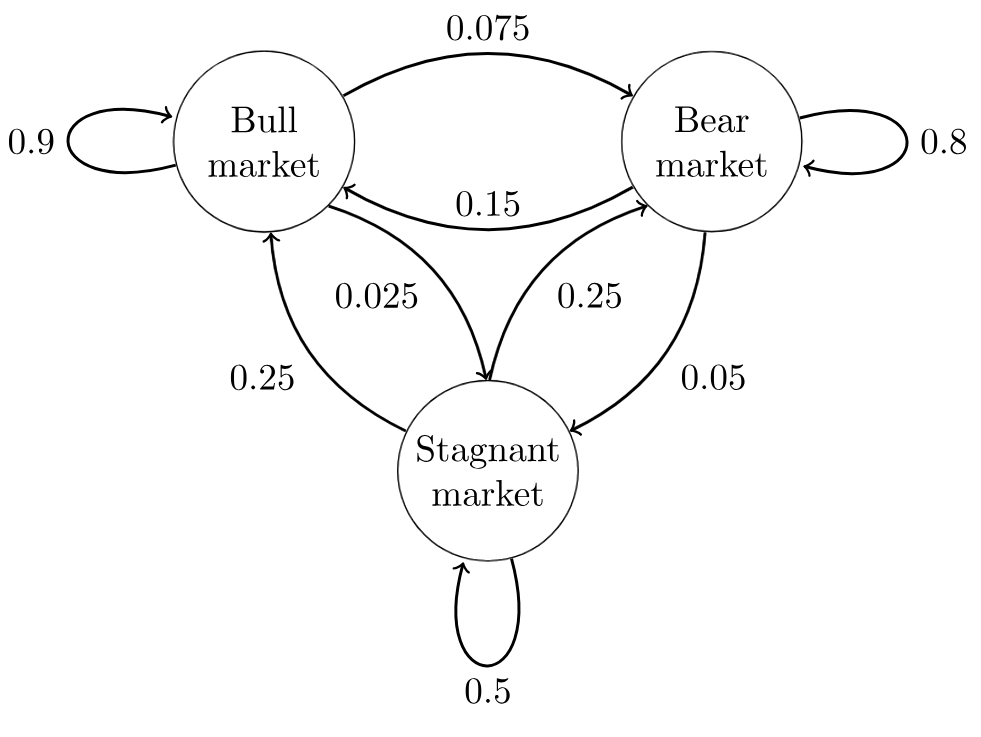
Markov Chain도 똑같습니다. 여러 상태들 $\left(x_1, x_2, \cdots, x_n, \cdots\right)$이 있고 $x_i$에서 $x_j$로 이동할 조건부 확률분포 transition distribution $T(x_j \vert x_i)$이 주어져 있어서 매턴마다 이 확률 값에 따라 상태들 사이를 이동하는 것입니다. 그렇다면 확률이 정해져 있다면 동선에 특정한 패턴이 존재하지는 않을까요? 예를 들어, “100번 이동했다면 평균적으로 3번은 출발지점에 돌아올 것이다”와 같은 예측을 할 수도 있을 것 같습니다.
예 맞습니다. 항상은 아니지만 확률이 정해져 있으므로 “특정조건”을 만족할 때 일정한 패턴이 나타납니다. 어떤 지점에서 시작하더라도, 상태 사이를 충분히 많은 횟수 이동하게 되면 각 상태의 방문횟수의 비율이 일정한 값으로 수렴하게 됩니다. 다시 말하면, 상태들의 방문횟수의 비율이 특정 확률분포로 수렴하게 되고 이 분포를 stationary distribution이라 부릅니다. “특정조건”에 대해서 더 궁금하신 분은 Markov Chain을 더 심도있게 공부해보시길 추천드립니다.
MCMC 속 Markov Chain
어쩐지 Markov Chain의 일정한 패턴이 앞에서 언급한 MCMC의 특성과 비슷해보이지 않나요? 맞습니다. 사실 MCMC에 Markov Chain이 정확히 녹아들었기 때문입니다. Markov Chain의 상태들을 이동하면서, 매번 이동했던 상태가 MCMC의 표본이 되는 것입니다. 결국 Markov Chain의 특성에 의해 MCMC들의 표본들은 정확히 우리가 원하는 target distribution $p(x)$을 반영하게 됩니다.
그렇다면 다음 단계는 stationary distribution이 target distribution $p(x)$가 되도록 Markov Chain을 잡는 것입니다. 앞에서 “특정조건”에 대해서는 자세히 설명하지 않았는데 그 이유가 있습니다. 왜냐하면 detailed balance라 불리는 다음의 간단한 식 하나를 만족시키면 “특정조건”이 성립하기 때문입니다. (역은 성립하지 않습니다.)
$p(x)T(y \vert x) = p(y) T(x \vert y)$
여기서 $x, y$는 임의의 두 상태 입니다. 이 식을 어떻게 사용하는지는 다음 알고리즘 단원에서 자세히 알아보겠습니다.
마지막 단계는 앞에서 설정한 Markov Chain으로부터 상태간의 이동을 의도한 확률 대로 구현하는 것입니다. 이 단계를 어떤 방식으로 구현하냐에 따라서 MCMC의 여러 알고리즘이 나눠지게 됩니다.
Metropolis-Hastings 알고리즘을 익혀보자
대부분의 MCMC 알고리즘들은 모두 Metropolis-Hastings(MH)의 특별한 경우이거나 MH를 확장한 알고리즘입니다. 따라서 MH가 MCMC의 가장 기본적인 알고리즘이라고 할 수 있습니다. 알고리즘이 짧지만 쉽지는 않기 때문에, pseudo code를 적기보다는 알고리즘의 흐름을 말로 풀어서 설명하겠습니다.
말로 풀어쓴 Metropolis-Hastings 알고리즘
1.
Target distribution을 $p(x)$라 합시다. MH는 $p(x)$에 비례하는 어떤 함수 $f(x)$를 계산할 수 있을 때 $p(x)$를 MCMC샘플링 할 수 있는 알고리즘입니다. 즉, $p(x)$를 몰라도 알고리즘이 성립합니다.
2.
그렇다면 $f(x)$만으로 $p(x)$를 샘플링 할 수 있을까요? 아쉽게도 $q(x^{t} \vert x)$라는 쉽게 샘플링이 가능한 조건부 확률 분포 proposal distribution이 더 필요합니다. 이름에서도 알 수 있듯이 이 분포는 알고리즘을 설계하는 개발자가 직접 제안하는 확률 분포입니다.(주로 정규분포를 이용합니다) MCMC기법은 다음 샘플을 뽑을 때 이전 샘플을 참고한다고 했습니다. 이전 샘플의 참고를 도와줄 함수가 바로 $q(x^{t} \vert x)$ 입니다. 이전 상태 $x$로 부터 다음 상태 $x^{t}$를 예측하려는 목적입니다.
3.
그런데 transition distribution $T(x^{t} \vert x)$가 있는데 왜 굳이 $q(x^{t} \vert x)$가 필요할까요? 그 이유는 바로 $T(x^{t} \vert x)$값을 정확히 알 수도 없고 샘플링 할 수도 없기 때문입니다. Detailed balnce를 만족하는 $T(x^{t} \vert x)$의 존재를 추상적으로 인식할 뿐, 직접 값을 설정할 수는 없습니다. 즉, $T$를 통해서는 다음 샘플을 뽑을 수가 없습니다. 그래서 $q(x^{t} \vert x)$라는 보조 함수를 통해 현재 샘플 $X_i$로 부터 임시 샘플 $X^{t}$을 뽑고 $q(X^{t} \vert X_i)$와 $T(X^{t} \vert X_i)$의 차이를 통해 $X^{t}$을 다음 샘플로 인정할지 기각할지를 결정하게 됩니다.
4.
$T(X^{t} \vert X_i)$가 $q(X^{t} \vert X_i)$보다 크다면 재빨리 $X^{t}$를 인정하는게 이득입니다. 원래 $T$로는 잘 샘플되는 $X^{t}$인데 보조수단인 $q$로는 그렇지 않기 때문에 기회가 왔을 때 인정하는게 좋습니다. $T(X^{t} \vert X_i)$가 $q(X^{t} \vert X_i)$보다 작다면, 얼마나 작은지에 따라 $X^{t}$를 인정해야 하므로 $T(X^{t} \vert X_i)/q(X^{t} \vert X_i)$의 확률로 인정하면 합리적일 것입니다. 따라서 acceptance ratio를 다음과 같이 정의합시다.
$A(x^{t} \vert x) = {T(x^{t} \vert x) \over q(x^{t} \vert x)}$
5.
하지만 식에 계산이 불가능한 $T$가 있으므로 detailed balance 식을 이용해 다음과 같이 $T$를 소거하고 계산 가능한 $f$로 대체해봅니다.
${A(x^{t} \vert x) \over A(x \vert x^{t})} = {T(x^{t} \vert x)/q(x^{t} \vert x) \over T(x \vert x^{t})/q(x \vert x^{t})} = {p(x^{t})q(x \vert x^{t}) \over p(x)q(x^{t} \vert x)} = {f(x^{t})q(x \vert x^{t}) \over f(x)q(x^{t} \vert x)}$
이 식을 만족하는 $A(x^{t} \vert x), A(x \vert x^{t})$ 쌍은 많이 있지만, Metropolis는 다음과 같이 설정했습니다.
$A(x^{t} \vert x) = \min\left(1, {f(x^{t})q(x \vert x^{t}) \over f(x)q(x^{t} \vert x)}\right)$
이러면 위 식을 완벽히 만족할 뿐더러 더이상 ratio가 아닌 probability로서 기능하게 됩니다. 따라서 다음 샘플 $X_{i+1}$은 $A(X^{t} \vert X_i)$의 확률로 $X^{t}$로 인정하고 $1 - A(X^{t} \vert X_i)$의 확률로 $X_i$로 유지합니다.
6.
하지만 알고리즘에 의심스러운 부분이 있습니다. $T$만 있었을 때와는 달리 $q$가 등장하고 $A$가 등장하니, 과연 처음에 의도했던 Markov Chain을 따라서 움직일지 확신하기가 어렵습니다. Metropolis-Hastings는 이러한 의문을 다음과 같은 논리로 해결합니다.
- MH 알고리즘은 $T$가 만드는 Markov Chain 1과는 별개로 또 다른 (stationary distribution을 가지는) Markov Chain 2를 만든다.
- 수학적으로 Markov Chain 1의 stationary distribution과 Markov Chain 2의 stationary distribution이 같음을 증명할 수 있다. (증명의 개요가 궁금하신 분들은 이 곳을 참조해주세요.)
장점, 단점 및 구현
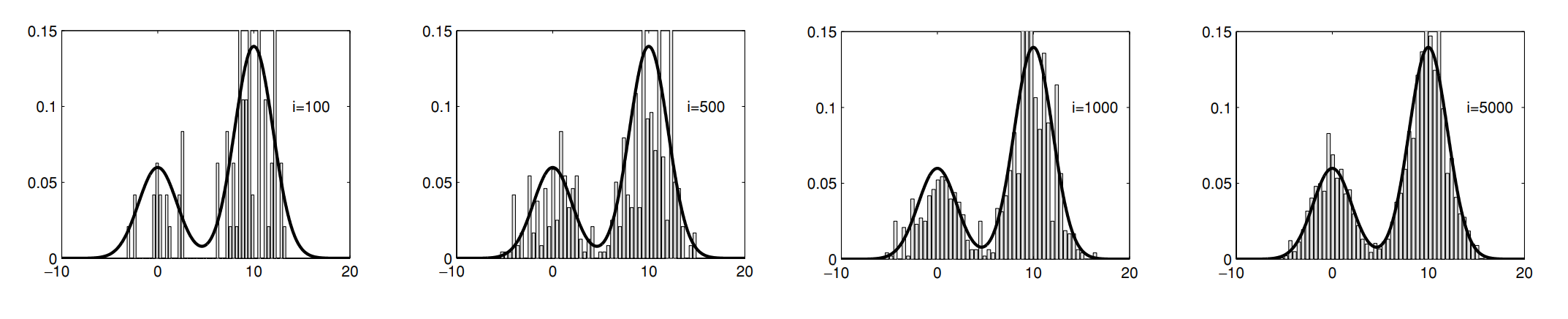
즉, 요약하면 MH는 target distribution $p(x)$에 비례하는 $f(x)$와 $p(x)$와 domain을 공유하는 임의의 proposal distribution $q(x^{t} \vert x)$이 주어졌을 때, $p(x)$에 대한 MCMC샘플링을 하는 알고리즘 입니다. 다음 그림은 실제로 proposal distribution $q(x^{t} \vert x)$를 “평균을 $x$, 분산을 100으로 하는 정규분포”로 설정하고 target distribution을 $p(x) \propto 0.3e^{-0.2x^2} + 0.7e^{-0.2(x-10)^2}$로 설정했을 때 MH가 샘플링하는 과정을 나타낸 것입니다.

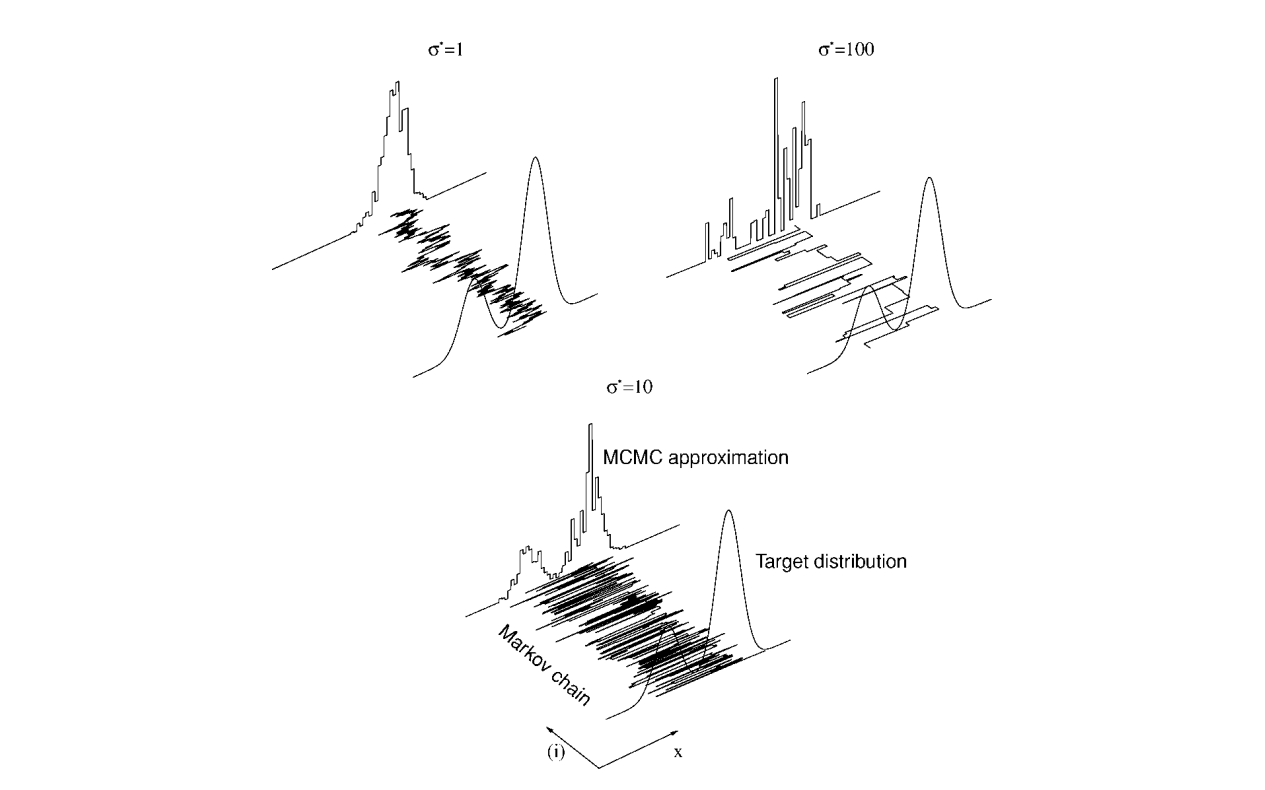
이렇게 보니까 MH가 정말 완벽한 알고리즘 처럼 보입니다. Proposal distribution을 아무거나 골라도 항상 수렴하니까요. 하지만 MH의 한 가지 결점은 proposal distribution에 따라 수렴속도의 차이가 심하다는 것입니다. 예를 들어 proposal이 정규분포일 때를 봅시다. 정규분포의 분산이 매우 낮으면, 자주 accept되는 대신 상태 공간에서 샘플간의 이동 거리가 매우 작을 것입니다. 그래서 만약 target distribution에 봉우리가 여러개 있다면 가장 높은 봉우리에서만 샘플링이 되는 것처럼 보이게 됩니다. 사실은 수렴속도가 느리다고 말하는게 정확합니다. 반대로 분산이 매우 높으면, 상태 공간에서 샘플 간의 이동 거리가 큰 대신 적게 accept 될 것입니다. 결과적으로 샘플들이 넓게 퍼져있지만 정돈되지 않은 형태가 보이게 됩니다. 역시 수렴속도가 느린 경우에 해당합니다. 그렇다면 수렴속도를 빠르게 하려면 자연스럽게 너무 작지도 않고 크지도 않은 분산을 설정하는게 중요해집니다. 다음 그림이 이 논의를 시각적으로 단번에 보여줍니다.
앞에서 언급했듯이 MH는 원리의 복잡성에 비해 구현은 굉장히 간단합니다.
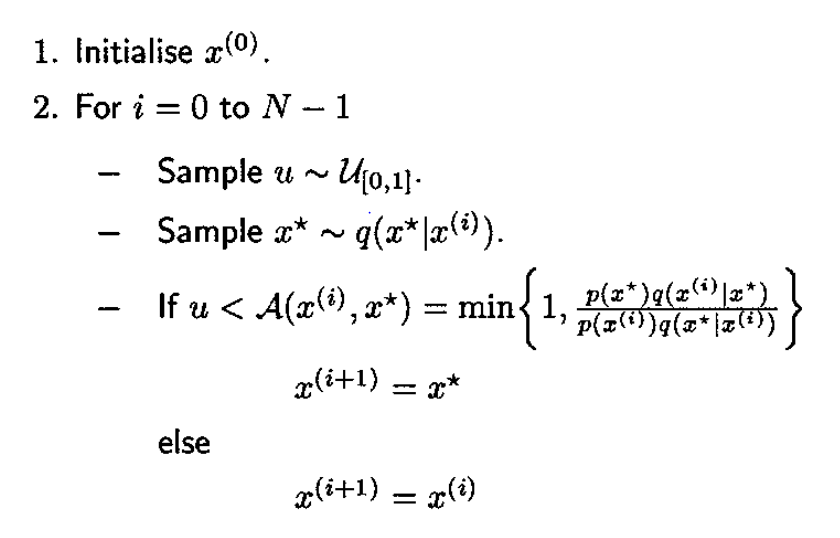
적절한 proposal을 선택한다면 여러분도 MH알고리즘으로 MCMC 샘플링을 충분히 할 수 있습니다. 이 글이 도움이 되었으면 좋겠습니다.