효율적인 긴 문자열 연산을 위한 Rope 자료구조
GCC , rope , algorithm , data-structure , string
로프와 쿼리
최근 백준 온라인 저지에 로프와 쿼리라는 이름의 베타 문제가 올라왔습니다. 그런데 문제 본문의 어디를 보아도 로프라는 단어는 쓰이지 않고, 줄과 관련되어 보이는 부분도 없습니다. 그저 문자열의 일부를 잘라서 앞이나 뒤로 옮기는 쿼리를 수행하는 문제일 뿐입니다. 그러면 이 문제의 이름은 왜 로프와 쿼리인 걸까요?
일반적인 문자열 자료구조로는?
우선 이 문제를 단순한 std::string 객체로 해결을 시도해 봅시다.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
string s;
cin >> s;
int q;
cin >> q;
while (q--)
{
int a, x, y;
cin >> a;
switch (a)
{
case 1:
cin >> x >> y;
s = s.substr(x, y - x + 1) + s.substr(0, x) + s.substr(y + 1);
break;
case 2:
cin >> x >> y;
s = s.substr(0, x) + s.substr(y + 1) + s.substr(x, y - x + 1);
break;
case 3:
cin >> x;
cout << s[x] << '\n';
}
}
}
1번 쿼리는 주어진 부분문자열, prefix, suffix를 순서대로 붙이고, 2번 쿼리는 prefix, suffix, 주어진 부분문자열을 순서대로 이어붙이는 풀이입니다. 하지만 뭔가 꺼림칙합니다. 이렇게 substr를 마구잡이로 사용하는 것이 과연 충분히 빠를까요?

안타깝게도 시간 초과를 받고 말았습니다. 예상한 대로, string::substr는 잘라내는 문자열의 길이에 비례하는 시간이 걸리고, 잘라낸 문자열끼리 붙이는 연산도 뒤쪽 문자열의 길이만큼의 시간이 소요되기 때문에, 총 $O(NQ)$의 복잡도를 피할 수 없게 됩니다.
사실 이 문제는 범위가 아주 크지는 않기 때문에 memmove 등을 이용하면 $O(NQ)$ 복잡도로도 충분히 통과될 수는 있습니다. 그러나 이는 문자열의 길이가 길어지면 길어질수록 점점 비효율적이 될 것이 명백합니다. 이렇게 긴 문자열을 자유자재로 지우고 자르고 붙이기 위해서 필요한 좋은 자료구조가 없을까요?
rope를 사용하면 해결!
문제 이름에 있는 rope는 사실 이런 문제를 해결하기 위한 자료구조의 이름입니다. 편리하게도, 이 자료구조는 gcc 확장에 이미 구현되어 있습니다! rope를 사용하여 문제를 해결한 코드는 다음과 같습니다.
#include <bits/stdc++.h>
#include <ext/rope>
using namespace std;
using namespace __gnu_cxx;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
crope rp;
string s;
cin >> s;
rp.append(s.c_str());
int n = s.size();
int q;
cin >> q;
while (q--)
{
int a, x, y;
cin >> a;
switch (a)
{
case 1:
cin >> x >> y;
rp = rp.substr(x, y - x + 1) + rp.substr(0, x) + rp.substr(y + 1, n);
break;
case 2:
cin >> x >> y;
rp = rp.substr(0, x) + rp.substr(y + 1, n) + rp.substr(x, y - x + 1);
break;
case 3:
cin >> x;
cout << rp.at(x) << '\n';
}
}
}
crope는 rope<char>와 같습니다. 즉, char형들을 원소로 가지는 rope 클래스입니다. string으로 문제를 해결할 때와 같이 substr로 부분문자열들을 잘라서 다시 조합하는 방식을 사용합니다. 그러나 아까와는 달리 신기하게도 substr 연산의 시간이 $O(N)$보다 작기 때문에, 시간 제한 내에 연산을 수행할 수 있습니다.

그러면 도대체 이 rope는 어떤 자료구조일까요? 그 정체를 간단하게 알아봅시다.
Rope
Rope는 매우 긴 문자열들에 대한 연산(자르기, 붙여넣기, 끼워넣기 등)을 효율적으로 처리하기 위해 고안된 자료구조입니다. 예를 들면, 텍스트 편집기에서 임의의 위치에 빠르게 접근하면서도 문자를 자유롭게 중간에 삽입하고 지우는 작업을 평범한 배열의 형태로 처리하기 위해서는 연산이 수행될 때마다 그 뒤에 있는 모든 문자들을 전부 앞으로 당기거나 미는 작업이 동반되어야 하기 때문에 매우 느릴 수 있는데, rope는 이런 문제를 해결하기 위한 더 빠른 방법을 제시해 줍니다.
기본 구조
Rope는 이진 트리의 형태로 구성됩니다. 트리의 리프 노드들은 각각 하나의 문자열과 그 길이를 가지고 있고, 리프 노드가 아닌 노드들은 그 노드의 왼쪽 서브트리에 있는 모든 리프 노드들의 길이의 합을 가지고 있습니다.
예를 들어, 아래 그림은 “software” 라는 문자열을 저장하는 로프의 예가 될 수 있습니다. 이 글에서는 이 그림을 예시로 사용합니다.
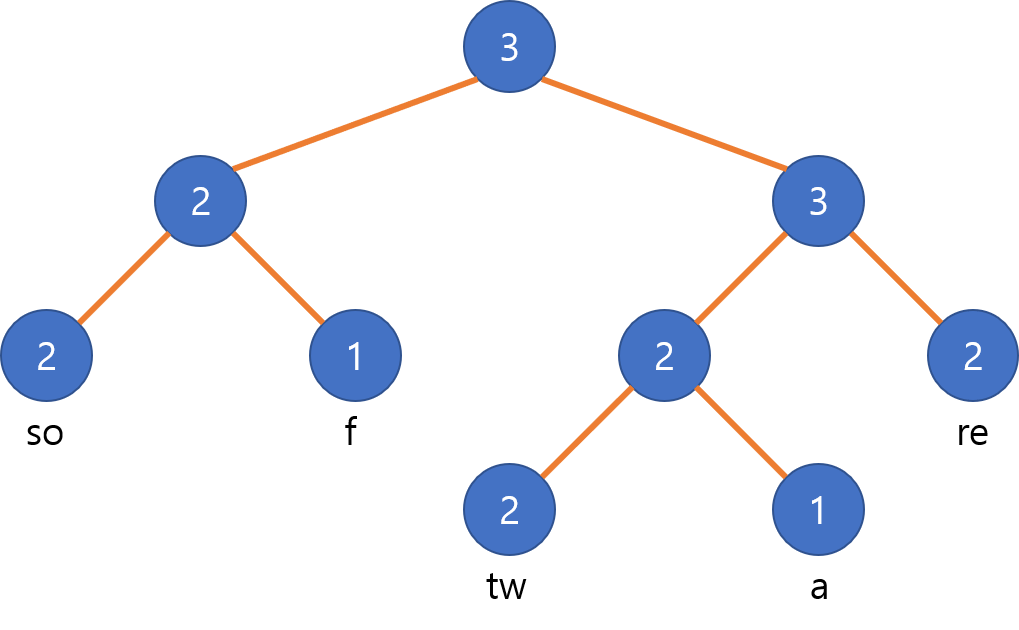
여느 이진 트리가 그렇듯이, 트리의 균형이 맞지 않으면 연산들이 나쁜 시간복잡도가 가능성이 크기 때문에 기준에 따라 균형을 다시 맞추는 작업도 요구됩니다. 이 글에서 자세히 다루지는 않지만, 안정적인 시간으로 동작하는 로프를 설계한다면 중요한 부분이 될 것입니다.
연산
인덱싱
로프의 특정 위치의 문자를 얻어오는 것은 간단합니다. 각 노드는 자신의 왼쪽 서브트리에 있는 모든 문자열의 길이의 합을 가지고 있기 때문에, 찾고자 하는 인덱스가 자신이 들고 있는 길이보다 작으면 왼쪽 서브트리로, 그렇지 않다면 오른쪽 서브트리로 재귀적으로 내려가면 됩니다. 왼쪽으로 내려갈 때는 인덱스를 그대로 가져가고, 오른쪽으로 내려갈 때는 노드에 기록된 길이만큼을 빼서 내려갑니다. 리프 노드에 도달했다면 그대로 인덱싱을 해서 문자를 얻어오면 됩니다.
예를 들어, 위의 예시에서 4번째(0-indexed) 문자를 찾는 과정은 다음과 같습니다.
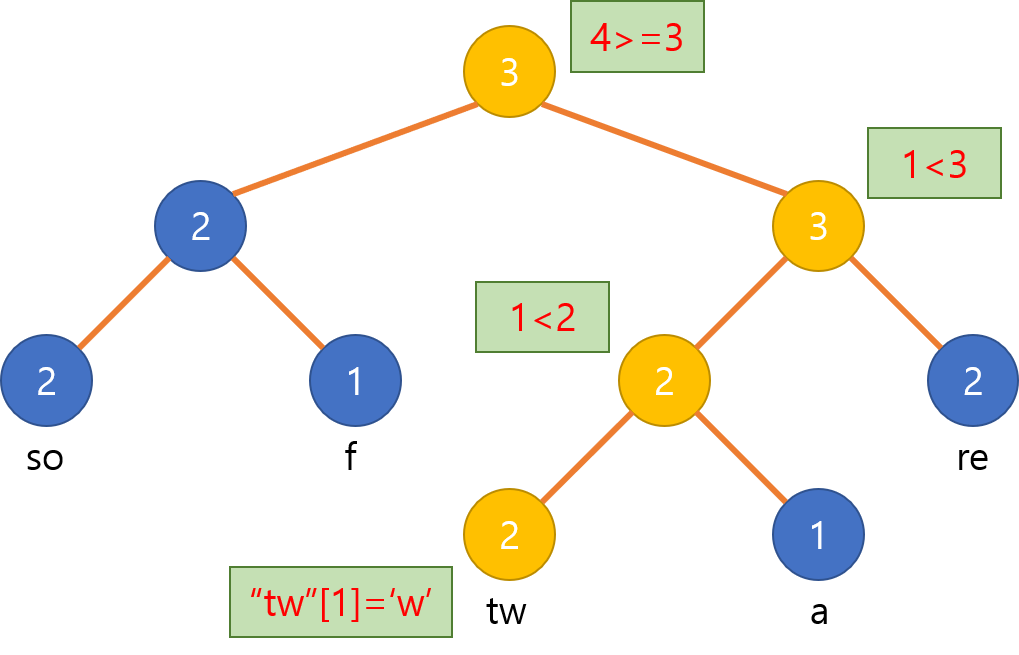
이어붙이기
이어붙이기는 새로운 루트 노드를 하나 만들고, 이어붙이려는 두 로프의 루트 노드들을 각각 왼쪽, 오른쪽 서브트리로 삼는 것으로 끝납니다. 여기까지는 $O(1)$이지만, 새 노드의 길이를 계산해주기 위해서는 왼쪽 서브트리에서 오른쪽 자식을 따라 리프 노드까지 내려가면서 합을 구해줘야 하므로 총 $O(logN)$ 시간이 소요됩니다.
위의 예시는 다음과 같이 “sof”라는 로프와 “tware”라는 로프 둘을 이어붙일 때 루트 노드가 만들어지고 양쪽 자식으로 붙어서 완성될 수 있습니다.
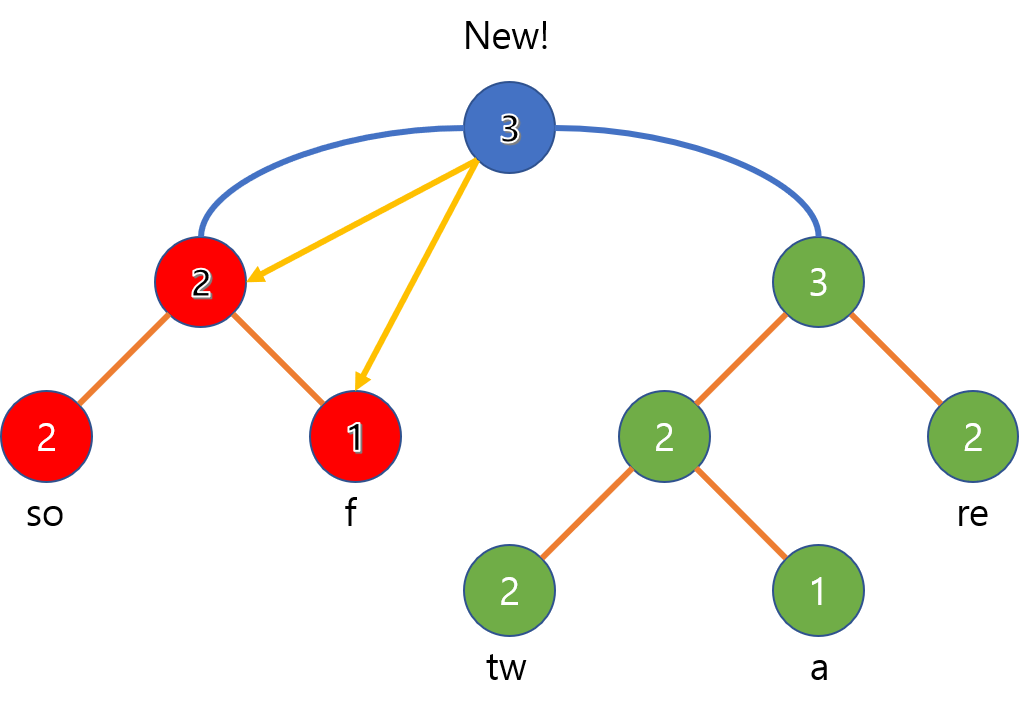
나누기
하나의 로프를 두 부분 로프로 나누기 위해서는 문자열에서 자르고 싶은 인덱스 이전을 나타내는 노드와, 이후를 나타내는 노드로 나누어서 분할하면 됩니다. 예를 들어, $i$번째 문자를 기준으로 나누고 싶다면, $i$번째 문자를 포함하는 리프 노드를 찾은 뒤, 부모로 올라가면서 각 노드의 오른쪽 자식이 $i$ 이후의 인덱스에 속하는 문자들만 포함한다면 연결을 끊어버립니다. 또한 왼쪽 자식에서 올라간 경우 부모의 길이도 갱신해 줍니다.
그 후 오른쪽 로프에 연결이 끊어진 노드들에게 새로운 부모들을 만들어 주고 다시 하나의 트리가 될 때까지 연결시켜가면 됩니다. $O(logN)$시간이 소요되고, 작업 이후 트리의 균형이 많이 꺠질 수 있기 때문에 균형을 다시 맞춰주어야 합니다.
위의 예시에서 “softw”와 “are”로 나누는 과정은 다음과 같습니다.
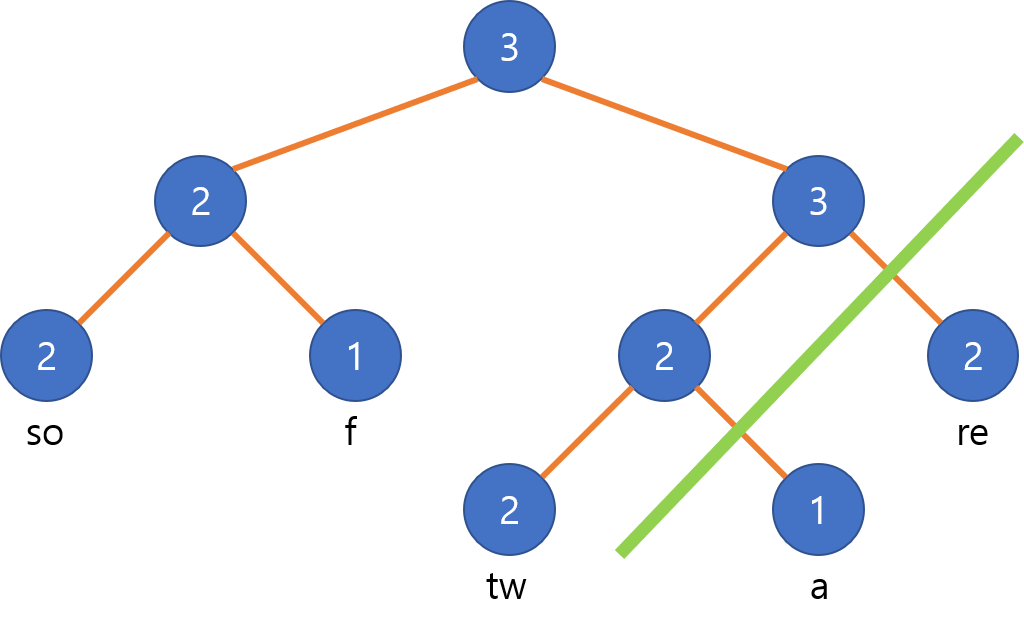
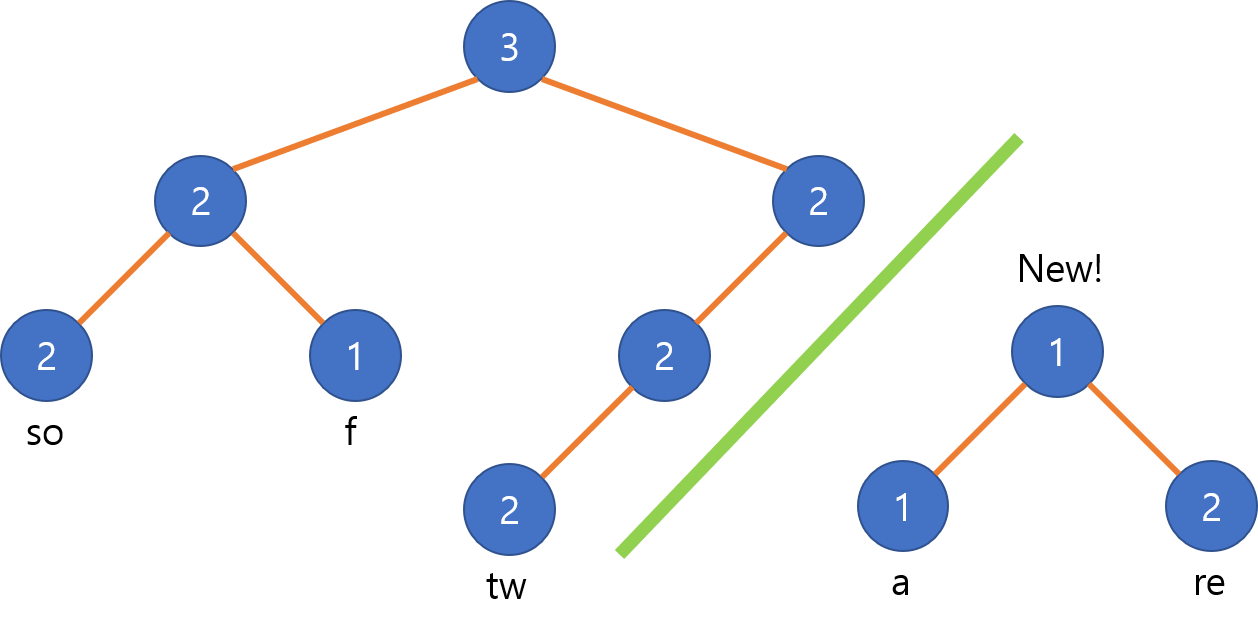
삽입
로프의 중간에 새로운 로프를 끼워넣는 작업입니다. 언뜻 보면 복잡해 보이지만, 사실은 위에서 살펴본 연산들을 조합해서 간단하게 해결할 수 있습니다. 먼저 끼워넣는 인덱스를 기준으로 두 개의 로프로 나눈 뒤, 왼쪽의 로프와 끼워넣는 로프를 이어붙인 뒤, 만들어진 로프와 오른쪽 로프를 다시 이어붙이면 됩니다.
삭제
삭제 역시 간단하게 구현이 가능합니다. 삭제될 부분의 왼쪽 끝과 오른쪽 끝을 기준으로 각각 나누기를 한 뒤 남은 왼쪽 로프와 오른쪽 로프를 다시 이어붙이면 됩니다.
부분문자열
여기서 부분문자열은 결과물을 통째로 반환하는 것이 아니라, 그 부분문자열을 표현하는 로프를 만들어내는 것을 뜻합니다. 이 연산은 부분문자열의 시작 인덱스와 끝 인덱스 방향으로 탐색해 들어가면서, 구간 내에 완전히 속하는 노드는 그대로 자식 노드로 가리키면 됩니다. 만일 양쪽 자식 노드 중 한 쪽의 일부에 구간이 걸쳐있다면 새로운 노드를 만들어서 다른 쪽 자식은 그대로 가리키고, 걸쳐있는 자식 쪽은 다시 재귀 호출을 통해 완전하게 범위에 들어오는 후손을 찾을 때까지 진행해나가는 식으로 구현할 수 있습니다. 최악의 경우 양 방향으로 각각 $O(logN)$ 개의 노드만 탐색하고 생성하면 되기 때문에 부분문자열 전체에 대한 로프를 새로 만드는 것에 비해 효율적입니다.
예시에서 [2, 5] 구간의 부분문자열 “ftwa”을 나타내는 로프를 만들어봅시다. 2번째 문자인 ‘f’를 통째로 담당하는 노드와, 3~5번째 문자열인 “twa”를 모두 담당하는 노드가 있으므로 이 둘을 자식으로 가지는 루트 노드 하나를 생성하면 됩니다. 기존의 로프에는 영향을 미치지 않습니다.
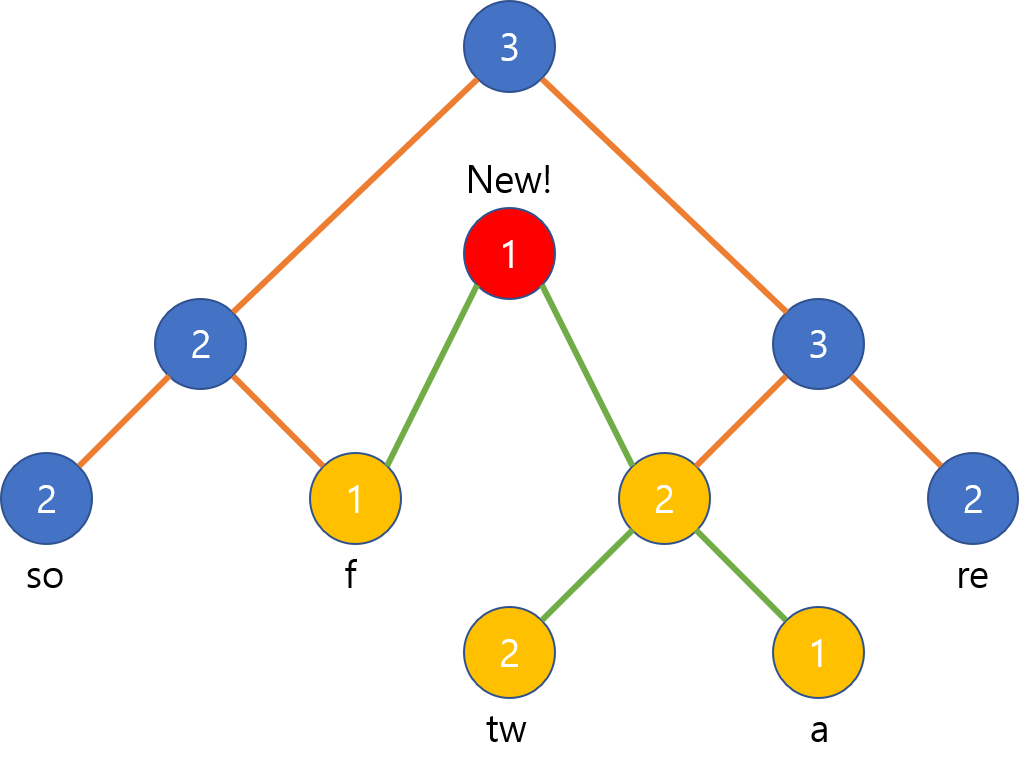
성능 측정
이제 rope 자료구조의 성능을 측정해 봅시다. 실험 환경은 VIrtualBox에서 Ubuntu 16.04 (64비트), g++ 7.3.0에서 -O2 옵션을 사용했습니다.
첫 번째 인자로 주어진 수만큼의 알파벳 소문자들로 이루어진 문자열을 만들고, 임의의 부분문자열 [a, b]를 잘라서 맨 앞이나 맨 뒤로 옮기는 작업을 두 번째 인자로 주어진 수만큼 수행합니다.
먼저 string으로 구현한 코드는 다음과 같습니다.
#include <bits/stdc++.h>
using namespace std;
int main(int argc, char *argv[])
{
ios::sync_with_stdio(false);
cin.tie(0);
string s;
int n = atoi(argv[1]);
int m = atoi(argv[2]);
for (int i = 0; i < n; i++)
s += char(rand() % 26 + 'a');
clock_t st = clock();
while (m--)
{
int b = rand() % n;
int a = rand() % (b + 1);
int x = rand() % 2;
if (x == 0)
s = s.substr(a, b - a + 1) + s.substr(0, a) + s.substr(b + 1);
else
s = s.substr(0, a) + s.substr(b + 1) + s.substr(a, b - a + 1);
}
cout << fixed;
cout.precision(3);
cout << (clock() - st) / double(CLOCKS_PER_SEC) << "s";
}
다음은 rope로 구현한 코드입니다.
#include <bits/stdc++.h>
#include <ext/rope>
using namespace std;
using namespace __gnu_cxx;
int main(int argc, char *argv[])
{
ios::sync_with_stdio(false);
cin.tie(0);
crope rp;
string s;
int n = atoi(argv[1]);
int m = atoi(argv[2]);
for (int i = 0; i < n; i++)
s += char(rand() % 26 + 'a');
clock_t st = clock();
rp.append(s.c_str());
while (m--)
{
int b = rand() % n;
int a = rand() % (b + 1);
int x = rand() % 2;
if (x == 0)
rp = rp.substr(a, b - a + 1) + rp.substr(0, a) + rp.substr(b + 1, n);
else
rp = rp.substr(0, a) + rp.substr(b + 1, n) + rp.substr(a, b - a + 1);
}
cout << fixed;
cout.precision(3);
cout << (clock() - st) / double(CLOCKS_PER_SEC) << "s";
}
두 코드에 대한 실험 결과는 다음과 같습니다. N과 M을 동일하게 설정하여 테스트한 값입니다.
1000: string = 0.001s, rope = 0.002s
5000: string = 0.007s, rope = 0.013s
10000: string = 0.019s, rope = 0.022s
20000: string = 0.046s, rope = 0.049s
50000: string = 0.548s, rope = 0.152s
100000: string = 2.774s, rope = 0.477s
200000: string = 12.242s, rope = 1.227s
300000: string = 27.034s, rope = 2.424s
500000: string = 58.086s, rope = 5.607s
규모가 작을 때는 오버헤드 때문에 rope가 오히려 조금 느리지만, 규모가 커지면 string은 급격하게 퍼포먼스가 나빠지는 반면에 rope는 완만하게 느려지는 것을 볼 수 있습니다.
응용
rope 라이브러리를 사용하면 본래 문자열의 중간에서 마구 잘라내지 못하게 설계된 문제도 거의 똑같은 코드로, string을 rope로 바꾸는 것만으로 무난하게 통과할 수 있습니다. 물론 의도된 $O(N)$ 알고리즘들에 비하면 훨씬 느리지만, 시간 내에 돌기에는 충분합니다.
#include <bits/stdc++.h>
#include <ext/rope>
using namespace std;
using namespace __gnu_cxx;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
crope rp;
string s, t;
cin >> s >> t;
rp.append(s.c_str());
int n = s.size();
int m = t.size();
int i;
for (i = 0; i < n; i++)
{
if (rp.substr(i, m).c_str() == t)
{
rp.erase(i, m);
i -= m;
}
}
if (rp.empty())
cout << "FRULA";
else
cout << rp;
}
- PPAP ```cpp #include <bits/stdc++.h> #include <ext/rope> using namespace std; using namespace __gnu_cxx;
int main() { ios::sync_with_stdio(false); cin.tie(0);
crope rp;
string s, ppap = "PPAP";
cin >> s;
rp.append(s.c_str());
int n = s.size();
for (int i = 0; i < n; i++)
{
if (rp.substr(i, 4).c_str() == ppap)
{
rp.erase(i + 1, 3);
i -= 2;
}
}
if (rp.c_str() == string("P"))
cout << "PPAP";
else
cout << "NP"; } ```