blisstoner's profile image

blisstoner

April 8, 2019 09:00

개요

차분 공격(Differential Cryptanalysis, 줄여서 DC라고 부르기도 함)는 선형 공격(Linear Cryptanalysis)와 더불어 블럭 암호를 공격하는 아주 강력한 공격 기법으로, 1991년 Eli Biham과 Adi Shamir(RSA을 만드신 그 분입니다!)에 의해 처음 논문으로 제시되었습니다.

NSA는 차분 공격을 1974년부터 인지하고 있었고 DES를 설계할 때 차분 공격으로부터 최대한 안전하게끔 만들었다고 추후에 밝혔습니다.

DES의 예시와 같이 비록 현대에 들어서는 블럭 암호를 설계할 때 차분 공격에 안전하게끔 설계를 하지만, Higher-order differential cryptanalysis, Truncated differential cryptanalysis, Impossible differential cryptanalysis, Boomerang attack과 같이 다양한 방식으로 변형된 공격 기법이 존재하기 때문에 아직까지도 블럭 암호를 분석할 때 유용하게 쓰이고 있습니다.

참고로 DES도 동시대에 제작된 다른 암호들에 비해 다소 차분 공격에 안전했지만 결론적으로는 1993년 Eli Biham, Adi Shamir가 $2^{47}$의 공격을 찾아냈습니다. 물론 현대에는 애초에 DES의 키가 56bit밖에 되지 않아 전수조사로도 금방 키를 복원할 수 있어 더 이상 DES를 사용하지 않지만, DES의 라운드를 조금 덜어낸 경우, 데스크탑으로도 20분 내로 키를 복원할 수 있습니다. 참고로 Shanghai Jiao Tong University의 해킹팀 0ops와 Tencent가 주최한 0CTF/TCTF 2019 Quals에 zer0des라는 이름의, Chosen Plaintext Attack 환경(선택 평문 공격, 임의의 평문에 대한 암호화 결과를 알 수 있는 환경)에서 8라운드 DES를 공격하는 문제가 출제되어 8팀이 정답을 맞추었고, 이 문제는 전체 문제들 중에 3번째로 정답자가 적은 문제였습니다.

이번 글을 통해 차분 공격이란 무엇인지를 같이 알아보고, 실제 DES의 차분 공격이 어떤 방식으로 이루어지는지를 공부해봅시다.

차분 공격이란?

차분 공격은 Chosen Plaintext Attack에서 사용할 수 있는 공격 기법입니다. 현대 암호의 경우 평문을 작은 데이터 단위로 나눈 후 Substitution과 Permutation을 반복 적용해 해독을 어렵게 만듭니다. 이 Substitution 과정이 비선형적이기 때문에 차분 공격이 나오기 전 까지는 키에 대한 전수조사 이외에는 마땅한 공격 방법을 찾지 못했지만, Substitution이 취약하게 설계되었을 경우 키의 XOR 여부와 관계 없이 차분은 유지된다는 성질을 이용해 키를 전수조사보다 효과적으로 유추할 수 있습니다. 실제 간단한 암호를 통해 예시를 들어보겠습니다.

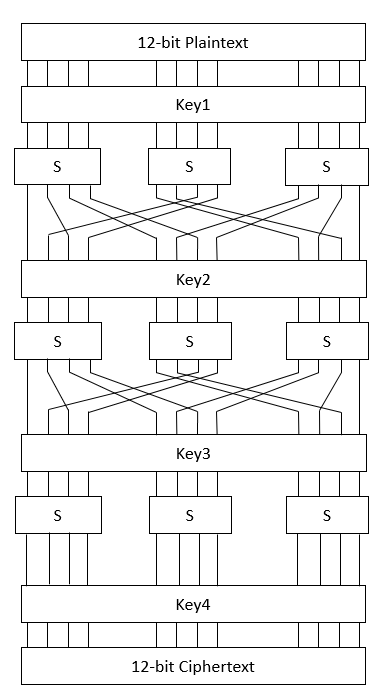
이 암호는 Substitution을 수행하는 S-box와 Bit permutation을 4라운드로 적용해 12-bit 평문을 12-bit 암호문으로 암호화하는 암호입니다. 이 과정에서 총 12-bit의 Key1, Key2, Key3, Key4이 Substitution 전에 XOR되는 용도로 쓰여 키는 총 48-bit입니다.

S-box는 4-bit를 입력으로 받아 4-bit를 출력하는 함수로, 테이블은 아래와 같습니다.

입력	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
출력	6	7	B	C	9	8	4	0	E	5	3	D	1	2	F	A

그리고 각 비트는 아래와 같이 이동합니다.

전	0	1	2	3	4	5	6	7	8	9	10	11
후	0	2	4	6	8	10	1	3	5	7	9	11

CPA 환경에서 암호문을 공격한다면 모든 평문 쌍에 대한 암호문을 수집해놓을 수 있으므로 $O(2^{12})$의 시간복잡도를 필요로 하고, 키를 찾고 싶다면 모든 키에 대한 전수조사를 필요로 하므로 $O(2^{48})$의 시간복잡도를 필요로 합니다. 그런데 이 S-box에는 취약점이 있습니다. 바로 입력의 차분에 대해 암호문의 차분이 그다지 균등하지 않다는 점입니다.

예를 들어 입력이 3과 5라고 해봅시다. 그러면 입력의 차분은 $3 \oplus 5 = 6$입니다. 그리고 3과 5의 출력은 각각 C와 8이므로 출력의 차분은 $C \oplus 8 = 4$입니다. 입력의 차분에 따른 출력의 차분은 0에서 F 사이의 임의의 값이므로 임의의 a, b에 대해 입력이 차분이 a일 때 출력의 차분이 b일 확률은 1/16일 것입니다. 그러나 해당 S-box에서 입력의 차분에 대한 출력의 차분은 아래와 같습니다.

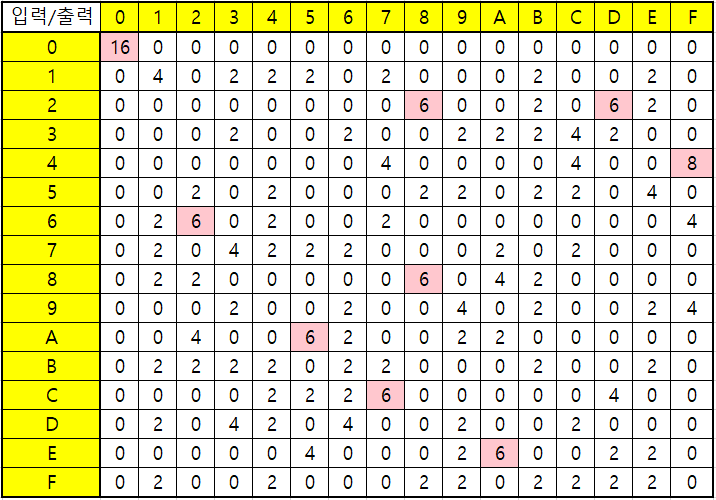
이렇듯 특정 입력과 출력의 차분에 대해서는 빈도수가 6 혹은 8과 같이 굉장히 높음을 알 수 있습니다. 이 성질을 이용해 Key4를 복원하기 위해서는 우선 적절한 차분 경로를 정해야 합니다. 차분 경로는 암호화 과정 중에 입력 차분이 전파되는 경로를 예상한 것으로, 위에서 확인한 확률 표에 따라 경로를 따라갈 확률을 예측할 수 있습니다. 저는 입력의 차분이 200일 때 차분 경로를 잡아보았습니다.

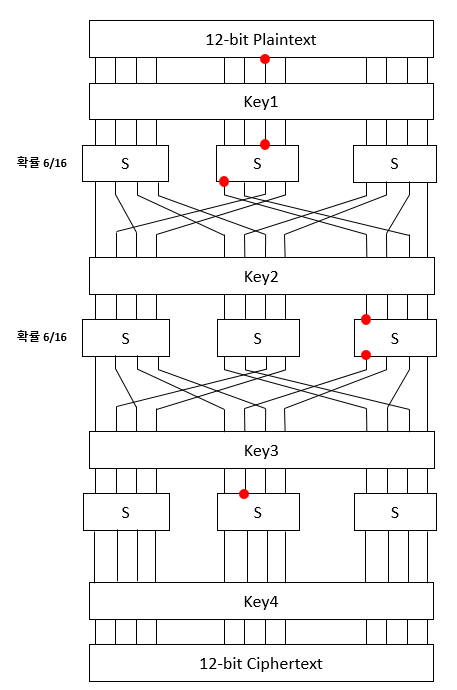
경로를 확인해보면 입력의 차분이 020일 경우 마지막 S-box를 거치기 전 중간 값의 차분이 040일 확률이 $\frac{6}{16} \times \frac{6}{16} = \frac{9}{64}$임을 알 수 있습니다. 비록 우리는 키들을 모르기 때문에 중간 값을 알 수 없지만, 만약 이 차분 경로를 따라온다면 암호문의 1, 3번째 nibble은 차분이 0이 되어야 함을 알 수 있습니다.(nibble은 4-bit를 의미하는 단위입니다.) 그러므로 일단 입력의 차분이 020인 쌍들을 무작위로 암호화시켜 암호문의 차분이 0?0인 쌍들을 수집합니다. 우리가 구한 확률에 따라 대략 7쌍을 확인하면 그 중에 한 쌍은 이 차분 경로를 따라가서 암호문의 차분이 0?0이 될 것입니다.

입력의 차분이 020이고 암호문의 차분이 0?0인 쌍들을 수집한 이후에는 Key4에서 12비트를 전수조사 하는 대신 오로지 중간 nibble 4비트를 따로 떼내어 복원해낼 수 있습니다. Key4의 중간 nibble의 값을 임의로 고정하고 암호문의 중간 nibble과 XOR한 뒤 S-box의 inverse를 계산합니다. 이렇게 계산한 inverse의 XOR이 4일 경우 이 값이 실제 Key4의 중간 nibble의 값일 확률이 굉장히 높습니다. 100% 확신할 수는 없지만 여러 쌍들에 대해 검증을 한다면 해당 키가 올바름을 확신할 수 있게 됩니다.

첫 번째와 세 번째 nibble의 경우도 마찬가지로 적절한 차분 경로를 찾아 복원이 가능합니다. 아래는 또 다른 차분 경로의 예시입니다.

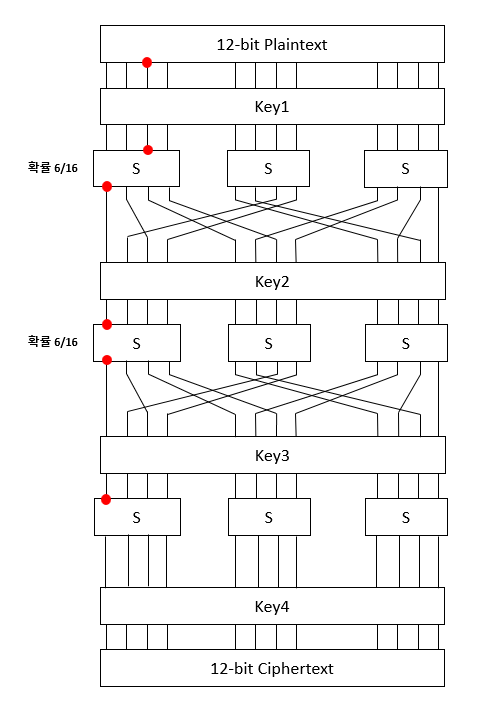
이번에는 입력의 차분이 200이고 출력의 차분이 ?00인 쌍을 여럿 찾아서 Key4의 첫 번째 nibble을 알아낼 수 있습니다. 이렇게 Key4를 복원한 이후에는 라운드가 하나 줄어든 셈이므로 Key3, Key2, Key1 모두 마찬가지 방법으로 복원해낼 수 있습니다.

차분 공격은 이와 같이 키의 비트를 나누어서 전수조사를 할 수 있게 해주는 공격입니다. S-box에서 입력의 차분에 대한 출력의 차분의 확률이 편중되어 있을 경우 확률이 높은 차분 경로를 만들기 쉬워져서 차분 공격이 더 쉽게 발생하게 됩니다.

DES에서의 차분 공격

DES에서의 차분 공격을 설명하기 이전, DES 암호화에 대한 이해를 하셔야 합니다. 그다지 이해가 어렵지는 않으니 위키피디아나 기타 자료를 참고해 직접 암호화 과정을 이해해보세요. 앞에서 언급했듯 DES는 설계 당시 차분 공격은 고려해 만들었습니다. Coppersmith님이 밝히신 DES의 설계 원리를 보면 나름대로 신경을 많이 썼다는 사실을 알 수 있습니다. 그 중에서 S-box와 관련한 부분을 살펴보겠습니다.

1. 각 S-box는 6-bit를 입력받아 4-bit를 출력합니다.
2. S-box에서 입력 비트와 출력 비트는 $1/2$에 가까운 확률을 가집니다.
3. S-box에서 양 끝 비트를 어떻게 잡더라도 중간 4-bit에 따른 출력 4-bit는 모두 다릅니다.
4. S-box에서 두 입력이 1비트만 차이날 경우 출력 비트는 적어도 2비트 이상 차이가 납니다.
5. S-box에서 입력 차분이 001100일 경우 출력 비트는 적어도 2비트 이상 차이가 납니다.
6. S-box에서 처음 두 비트가 다르고 뒤의 두 비트가 다를 경우 출력 비트의 차분은 0이 아닙니다.
7. S-box에서 임의의 입력 차분에 대해 동일한 출력 차분을 가지는 쌍은 최대 8개입니다.

이와 같이 S-box를 만들면 차분 경로를 찾는 것이 어렵거나, 찾는다고 하더라도 차분이 여러 S-box로 전파되면서 확률이 낮아져 차분 공격이 전수 조사보다 비효율적이게 될 것입니다. 그러나 Eli Biham, Adi Shamir가 1993년에 발표한 Differential Cryptanalysis of the Full 16-round DES 논문에서는 다양한 테크닉을 통해 이 문제를 극복하고 $O(2^{47})$개의 chosen plaintext로부터 $O(2^{37})$에 키를 찾을 수 있었는지를 같이 알아봅시다.

DES를 차분 공격하는데 쓰인 핵심적인 경로는 바로 입력 차분이 19 60 00 00 00 00 00 00일 때 $\frac{1}{234}$의 확률로 2라운드를 거친 후 출력 차분이 00 00 00 00 19 60 00 00이라는 경로입니다.

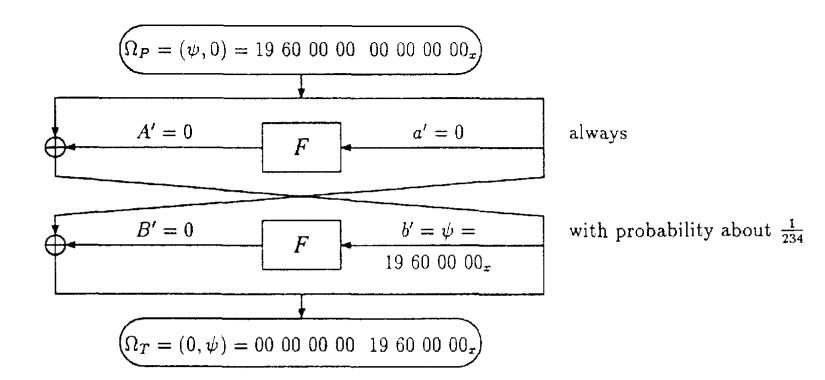
이 확률은 각 S-box의 입력과 출력을 비교해볼 때 S1에서는 입력 차분 000011에 대해 출력 차분 0000, S2에서는 입력 차분 110010에 대해 출력 차분 0000, S3에서는 입력 차분 101100에 대해 출력 차분 0000이 발생해야 하므로 각 확률 $\frac{14}{64}$, $\frac{8}{64}$, $\frac{10}{64}$을 곱해 나온 결과입니다.

문제는 DES가 총 16라운드이므로 이 경로만으로 해결을 하려고 들 경우 해당 경로를 적어도 7번은 거쳐야 하므로 확률은 $(\frac{1}{234})^6=2^{-55.1}$이 되어 전수조사와 다를 바가 없어집니다. 대신 이 논문에서 제안한 방법은 19 60 00 00 00 00 00 00을 이용한 경로로 13라운드를 해결하고, 확률을 더 나빠지게 하지 않도록 하면서 round를 추가하는 것입니다. 우선 논문에서 소개한 전체 차분 경로를 확인합시다.

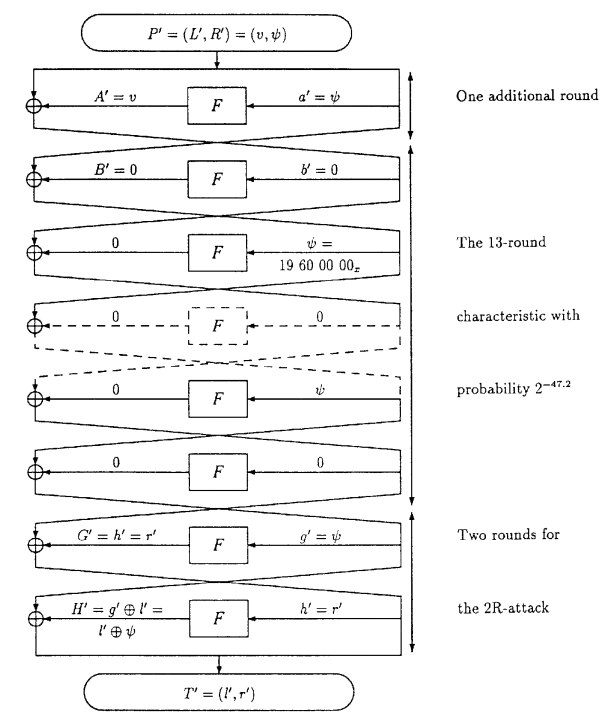
보면 14라운드까지는 19 60 00 00 00 00 00 00으로 진행하지만 마지막 2라운드에서는 뭔가 복잡한 방식으로 처리를 함을 알 수 있습니다. 이 처리는 확률을 더 나빠지게 하지 않도록 하기 위해 수행하는 처리로, 저희가 앞에서 살펴본 예시에서 마지막 라운드의 S-box에서는 차분을 정해두지 않고 그 어떤 차분이 나오더라도 키를 가지고 역연산을 수행하도록 한 것과 비슷한 방식을 사용합니다.

14라운드까지 올바른 경로를 따라왔다고 가정한다면, 15라운드에서 입력 차분이 19 60 00 00인 채로 S-box에 들어가게 됩니다. 그러면 S4, S5, S6, S7, S8에는 입력 차분이 0인 입력이 들어가므로 출력 차분 또한 0임은 자명합니다. Feistel 구조의 특성상 15라운드에서의 S-box 출력은 그대로 암호문의 오른쪽 32비트에 들어가게 되고, 이를 바탕으로 암호문에서 S4, S5, S6, S7, S8에 출력 차분이 0인 채로 나왔는지를 확인할 수 있습니다.

또한 15라운드의 출력이 16라운드에서 S-box의 입력으로 쓰이므로 16라운드에서는 모든 S-box의 입력 차분과 출력 차분을 알 수 있습니다. 만약 차분 분포 표 상에서 불가능한 입력 차분, 출력 차분이 나왔을 경우 올바른 경로를 따라오지 않았음을 알 수 있게 됩니다.

구체적으로 논문에 소개된 방법을 이해해봅시다. 우선 임의의 64-bit plaintext P를 정하고 $v_0$, $v_1$, $v_{4095}$를 P의 first round에서 S1, S2, S3의 output bit를 00 00 00부터 FF FF FF까지로 바꿔지게끔 하는 값이라고 해봅시다. 그러고나서 $P_i = P \oplus (v_i, 0)$으로, $Q_i = P_i \oplus $(00 00 00 00 19 60 00 00)으로 둔다면 $P_i$와 $Q_i$의 차분은 00 00 00 00 19 60 00 00이 될 것입니다. 그리고 $i, j = 0, 1, 2, \dots 4095$에 대해 $2^{24}$개의 $P_i, Q_i$ pair를 생각해보면 이들의 차분은 ($v_k$, 19 60 00 00)이 되고 각 $v_k$는 정확히 $2^{12}$번씩 등장합니다.

문제는 이 $2^{24}$개의 pair에서 어떻게 내가 생각한 19 60 00 00 00 00 00 00 경로를 타고 내려온 쌍을 찾는지가 문제인데, 만약 해당 경로를 타고 내려왔다면 반드시 암호문의 차분 상에서 S4, S5, S6, S7, S8로부터 도달한 비트는 0이 되어야 합니다. 그러니 $P_i$에 대한 암호문, $Q_i$에 대한 암호문에서 이 20비트의 값을 가지고 정렬을 하거나 해쉬를 이용해 20비트가 일치하는 쌍을 찾습니다. 그리고 추가적으로 15, 16라운드에서 S-box를 통과할 때 DES의 차분 분포 표 상으로 불가능한 값이 나오면 버립니다.

이 과정을 통해 모순이 생기지 않는 쌍을 찾고 나면 그 쌍은 올바른 경로를 따라왔을 확률이 있습니다. 이제 그 쌍을 바탕으로 키를 복구합니다. 우리는 1라운드, 15라운드, 16라운드에서 입력 2개와 출력의 차분을 알고 있습니다. 예를 들어 내가 1라운드의 세 번째 S-box에는 4, 8, 12, 19, 23, 26번째 키 비트가 쓰입니다. 즉 키는 총 64개가 가능한데, 입력 2개는 001100, 001001이고 출력 차분은 0001일 때 이를 가능하게 하는 키는 총 4개이므로 후보군을 줄일 수 있습니다. 1라운드의 세 번째 S-box와 16라운드의 네 번째 S-box는 3개의 키 비트가 겹치므로 16라운드의 네 번째 S-box에 대해서 마찬가지 작업을 통해 키 후보를 구하고, 이와 같이 1라운드와 16라운드를 오가면서 우선 Left Key 28 bit를 복원합니다.

그 후에는 15라운드와 16라운드를 오가면서 Right Key 28 bit또한 복원해낼 수 있습니다. 이렇게 복원해낸 키를 가지고 임의의 평문을 암호화했을 때 실제 암호화 결과와 일치한다면 키를 찾은 것이고, 그렇지 않다면 애초에 쌍이 올바른 경로를 따라온 것이 아니므로 다른 쌍을 가지고 마찬가지 과정을 진행합니다.

8라운드에 대한 대회 문제를 풀면서 코드를 나름 이쁘게 만들었는데, 대회 중에 다른 문제를 풀다가 실수로 코드를 날려먹었습니다ㅠ_ㅠ 대신 예전에 12라운드에 대한 공격을 진행한 것이 있어서 해당 코드를 참고해보시면 이해에 도움이 될 것입니다.(Repo 링크)

맺음말

이번 게시글에서는 그다지 응용이 들어가지 않은 차분 공격들을 예시로 다루었습니다. 그러나 마치 PS에서 단순히 알고리즘 하나를 안다고 끝나는 것이 아니라 수 많은 응용 방법들이 있는 것 처럼 차분 공격 또한 차분의 차분의 차분의 차분을 보는 High Order Differential Cryptanalysis, DES의 라운드키를 복원할 때 사용한 것과 비슷하게 입력의 차분에 따라 불가능한 차분이 존재할 경우 해당 키의 후보를 걸러내는 Impossible Differential Cryptanalysis, 전체의 차분을 정해두는 것이 아니라 일부의 차분만 정해서 공격하는 Truncated Differential Cryptanalysis 등의 다양한 응용 방안이 있습니다.

물론 실제로 개발을 할 때에는 현재까지 다양한 공격 시도 끝에도 중대한 취약점이 발견되지 않은 AES와 같은 암호를 그대로 가져와 사용할 것이기 때문에 이런 내용에 대해 잘 알지 못하더라도 상관이 없지만 장차 암호학을 전공할 계획이 있다면 알아둘만한 가치가 있는 공격이라고 생각합니다.