O(1) LCA Algorithm (with Sparse Table)
목표 및 문제 소개
LCA(Lowest Common Ancestor)란 루트가 정해진 트리에서, 두 노드 간의 공통 조상이면서 루트에서 가장 먼 노드를 뜻합니다. 노드가 $N$개인 트리에서 임의의 두 노드 간의 LCA를 쿼리당 $O(lgN)$에 구하는 알고리즘은 잘 알려져 있습니다. 각 노드별로 $ 2^k $ 번째 조상을 미리 계산해둔 뒤, Binary Lifting을 활용해 구하는 방식입니다. 이에 대한 지식이 부족하다면 링크 에서 먼저 공부한 뒤에 이 글을 읽으시는 것을 추천합니다. 이 글에서 소개하고자 하는 알고리즘과 밀접한 관련은 없지만, 전반적인 개념에 도움이 될 것입니다.
이 글에서는, $O(NlgN)$ 전처리 시간복잡도와, 쿼리당 $O(1)$ 시간복잡도에 LCA 쿼리를 처리하기 위한 알고리즘을 소개합니다. 이를 위해 Sparse Table과 Euler Tour on Tree의 두 개념을 먼저 설명한 뒤, 이 둘을 이용해 어떻게 쿼리당 $O(1)$ 시간복잡도에 LCA를 구할 수 있는지 설명하도록 하겠습니다. 최종적으로,(백준 11438) LCA2 문제를 해결하는 코드를 작성해 볼 것입니다.
사전지식1 - Sparse Table
일반적으로 잘 알려져 있는 Segment Tree 자료구조는 Range Minimum/Point Update 쿼리를 $O(lgN)$ 시간복잡도에 처리할 수 있습니다. Sparse Table 자료구조는 $O(NlgN)$ 시간복잡도로 전처리를 한 이후에는 Update가 불가능한 대신, Range Minimum 쿼리를 $O(1)$ 시간복잡에 처리할 수 있는 자료구조입니다.
$N$개의 원소가 들어있는 배열 $A$를 생각합시다. Sparse Table 자료구조 $ST$는 다음과 같은 2차원 배열로 선언됩니다.
int A[N];
int ST[LOGN][N];
$ST[k][i]$에 들어갈 값은, $min(A[i],\ A[i+1],\ … ,\ A[i+2^k-1])$ 이 됩니다. 즉, $i$부터 연속한$2^k$개의 원소들의 최솟값을 저장할 것입니다. $N$이 대략 ~40만정도 크기이면 $LOGN$은 20정도로 문제의 조건에 따라서 설정해주면 될 것입니다.
아래의 예시를 보면, 배열 $A$에 대해 Sparse Table $ST$를 채운 결과물을 확인할 수 있습니다.
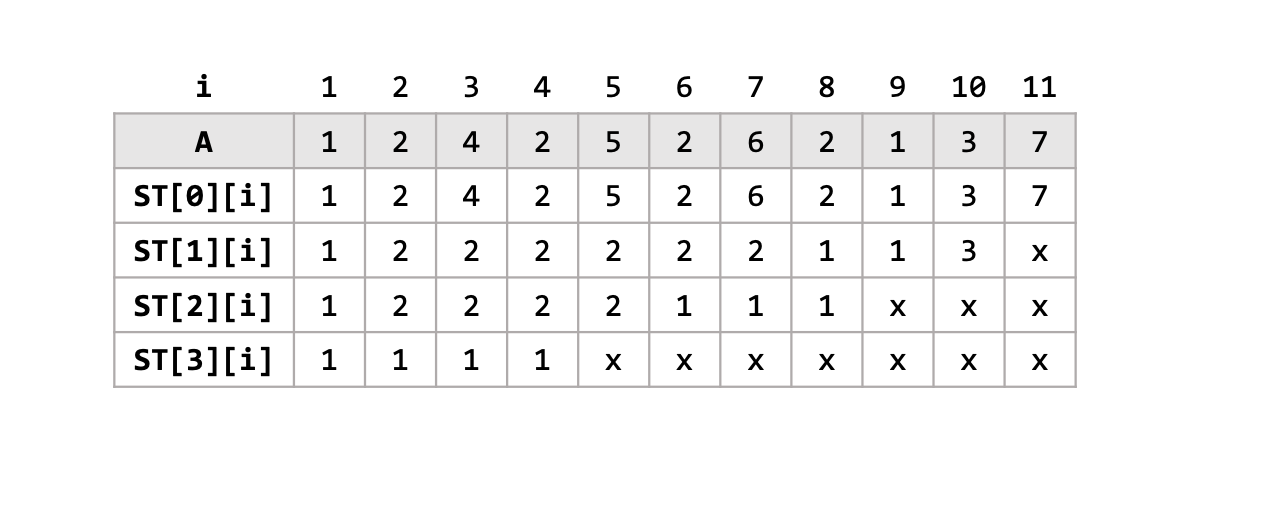
Sparse Table자료구조의 본체라고 할 수 있는 $ST$ 배열을 채우는 데에는 $O(NlgN)$ 시간복잡도면 충분합니다. $ST[k][i]$에 들어가는 값은 앞서 설명했듯이 $min(A[i], A[i+1], … A[i+2^{k-1}])$ 입니다. 이 구간을 절반으로 나누면 $min(\ min(A[i],\ A[i+1],\ … ,\ A[i+2^{k-1}+1]),\ min(A[i+2^{k-1}],\ A[i+2^{k-1}+1],\ … ,\ A[i+2^k-1]) )$ 으로 나타낼 수 있습니다. 그런데 나뉘어진 각 부분은 곧 $ST[k-1][i]$, $ST[k-1][i+2^{k-1}]$ 이므로, $ST[k][i] = min(ST[k-1][i],\ ST[k-1][i+2^{k-1}])$이 되어서 $O(1)$시간복잡도에 하나의 원소를 계산할 수 있습니다. 이를 $NlgN$개의 원소에 대해 계산해야 하므로, 최종 전처리 시간복잡도는 $O(NlgN)$이 됩니다.
이제 어떻게 구간 최솟값 쿼리를 $O(1)$ 시간복잡도에 수행할 수 있을까요? 임의의 구간 $[l…r]$은 어떤 $k$값이 존재해서 길이 $2^k$인 구간 두 개로 덮을 수 있음이 자명합니다. 아래 그림과 같이 첫 구간은 $[l…l+2^k-1]$ 이고, 두번째 구간은 $[r-2^k+1…r]$ 이 될 것입니다.

따라서 $min(A[l], … A[r])$은 곧 $min(ST[k][l], ST[k][r-2^k+1])$와 같이 단 두개의 $ST$원소로 계산할 수 있습니다.
자세한 구현은 글의 후반부에서 최종적으로 LCA를 구하는 코드를 작성할 때 다시 설명하도록 하겠습니다. 일단은 Range Minimum 쿼리를 쿼리당 $O(1)$ 시간복잡도에 수행할 수 있다는 것을 기억하고 진행합시다.
사전지식2 - Euler Tour on Tree
Euler Tour on Tree 는 임의의 (루트가 정해져 있는) 노드 $N$개짜리 트리를 길이 $2N-1$의 수열로 나타내는 방식입니다. 일반적인 DFS와 같은 방식으로 트리를 순회하면서, 노드를 만날 때마다 수열의 맨 뒤에 해당 노드를 추가해 줍니다. 여기서 한가지 다른 점은, 위로 되돌아 올라가는 퇴각 과정에서도 노드를 추가해준다는 것입니다. 아래 예시를 보면 이해가 될 것입니다. 시간 $t$에 따라서 수열이 어떻게 진행되는지 살펴보시길 바랍니다.
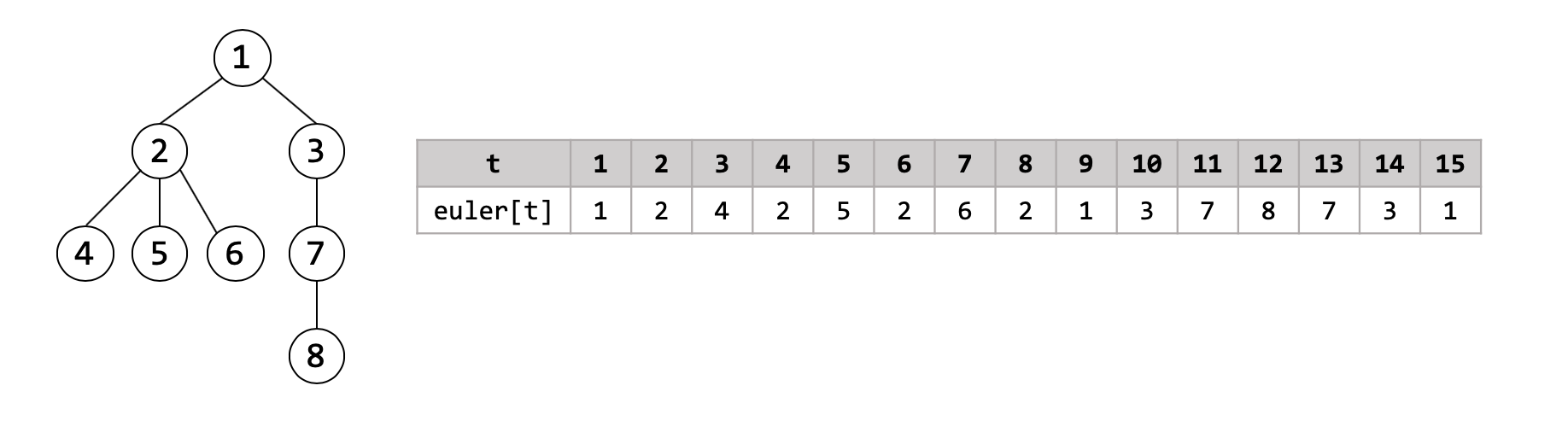
Euler Tour은 다음과 같은 몇가지 성질을 가지고 있습니다.
(1) 각 노드는 degree 횟수만큼 등장하고, 루트는 맨 처음에 한번 더 등장합니다. 노드가 $N$개인 트리의 간선 개수는 $N-1$개이므로 Euler Tour 의 길이는 $2N-1$이라는 것을 유도해낼 수 있습니다.
(2) Euler Tour에서 인접한 위치의 두 노드는 항상 깊이(level)차이가 1입니다. 이는 Euler Tour의 진행방식에서 자명합니다.
(3) 특정 노드의 서브트리는 DFS ordering과 비슷하게 구간으로 나타낼 수 있습니다. 노드 x의 서브트리는 x의 첫 등장 위치에서부터 마지막 등장 위치까지라는 것을 알 수 있습니다. Euler Tour의 진행방식이 DFS와 유사하므로 직관적으로 알 수 있습니다.
O(1)에 LCA 구하기
이제 Euler Tour와 Sparse Table을 함께 사용해 트리에서 임의의 두 노드의 LCA를 $O(1)$ 시간복잡도에 계산하는 방법을 알아봅시다. 먼저 아래와 같은 트리에서 4번 노드와 7번 노드의 LCA를 구하려 한다고 생각해 봅시다.
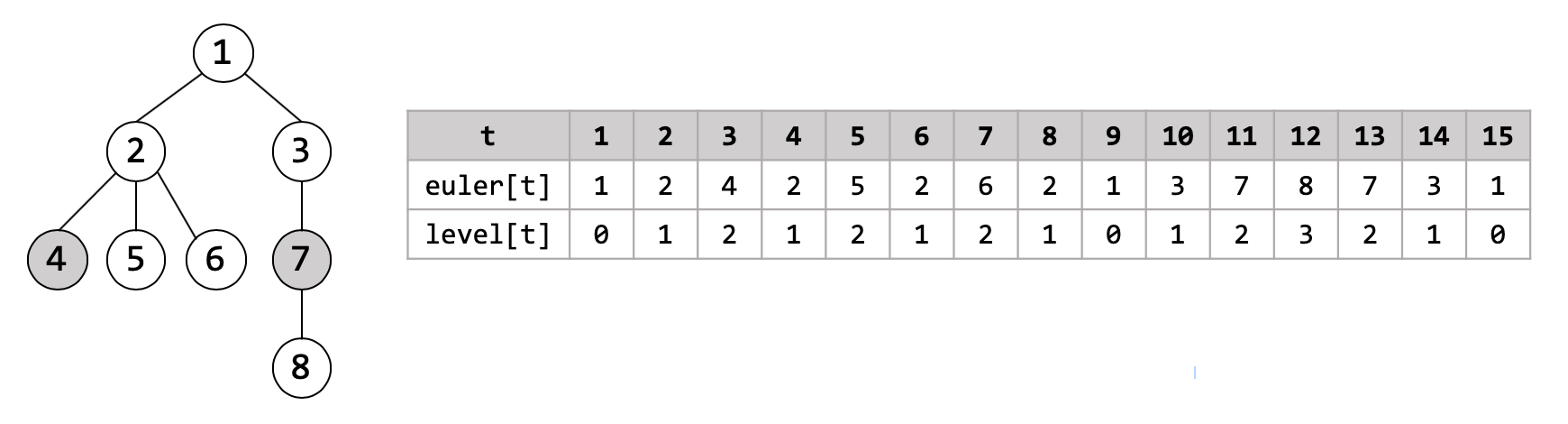
4번 노드와 7번 노드가 Euler Tour에서 등장하는 위치를 표시해 봅시다. 각 노드는 여러번 등장할 수 있지만, 아무 위치나 선택하면 됩니다. 그런 뒤, Euler Tour상에서 두 노드 사이에는 어떤 노드들이 등장하는지 살펴봅시다. 아래 그림과 같이 회색으로 색칠된 노드들이 포함될 것입니다 (여기에는 4,7번 노드도 포함됩니다).
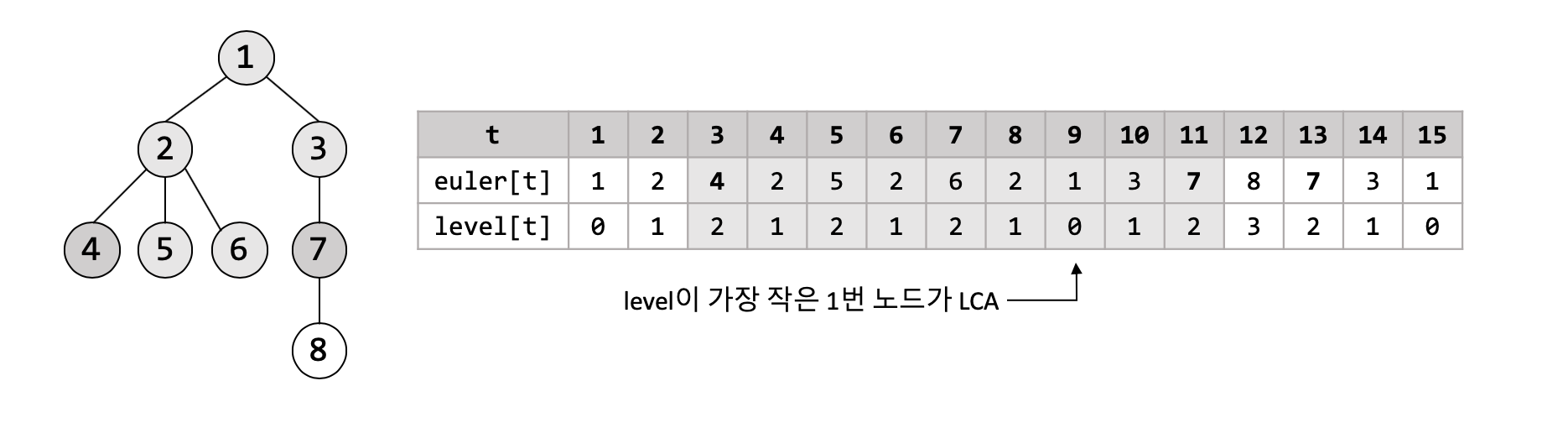
회색으로 색칠된 노드들을 잘 살펴보면, 모두 우리가 원하는 LCA보다 level이 크거나 같다는 것을 알 수 있습니다. Euler Tour가 진행되는 방식을 생각해 보면, LCA는 반드시 이 회색 노드들 중 하나라는 것을 알 수 있습니다. 4번 노드에서 7번 노드까지 가는 경로에 있는 노드들은 반드시 회색으로 색칠될 것인데, LCA는 이 경로상에 존재할 수밖에 없기 때문입니다. 또한, Euler Tour에서 특정 subtree는 구간으로 나타난다는 성질을 생각해 보면, LCA보다 level이 작은 노드가 회색으로 색칠될 일은 없다는 것을 알 수 있습니다. 위 관찰들로부터, 결국 회색 노드들 중 level이 가장 작은 노드가 바로 우리가 원하는 LCA라는 것을 알 수 있습니다. 이 경우에는 level이 0으로 가장 작은 1번 노드가 LCA로 구해지게 됩니다.
위에서 얻은 결론을 다시 정리하면, 노드 $u$, $v$의 LCA는, Euler Tour상에서 $u$, $v$사이에 등장하는 노드들 중 가장 level이 작은 노드입니다. (앞서 언급했듯, $u$, $v$가 여러번 등장한다면 어떤 것을 선택해도 관계없습니다) level이 가장 작은 노드를 구하는 것은 결국 Range Minimum Query와 다를 바가 없으므로 Sparse Table 자료구조를 이용해 쿼리당 $O(1)$ 시간복잡도에 해결할 수 있습니다. 따라서 임의의 두 노드의 LCA를 쿼리당 $O(1)$ 시간복잡도에 해결할 수 있게 되는 것입니다.
구현 및 문제 풀이
먼저 풀이에 사용될 몇가지 변수들을 정의합시다. 트리의 노드는 N개이고 쿼리의 개수는 Q개입니다. 간선들은 인접 리스트의 형태로 E에 저장되어 있습니다. 또한, idx에는 각 노드가 Euler Tour의 어느 시점에서 등장하는지 목록을 가지고 있도록 합니다.
#define MAXN 100100
#define LOGN 20
int N, Q, timer;
int euler[200200], lev[100200];
vector<int> E[200200], idx[200200];
트리를 입력받고 Euler Tour와 level배열을 채워넣읍시다. 일반적인 DFS 순회를 하면서 Euler Tour와 level 모두 계산할 수 있습니다. 이 과정에서 idx 리스트 또한 계산할 수 있습니다.
void dfs(int x, int pa, int l){
lev[x] = l;
euler[++timer] = x;
idx[x].push_back(timer);
for(int e : E[x]) if( e != pa ){
dfs(e, x, l+1);
euler[++timer] = x;
idx[x].push_back(timer);
}
}
이제 Sparse Table 자료구조를 구현합시다. pw2는 각 $k$마다 $2^k$값을 미리 계산해둔 배열이고, lg2는 구간의 길이에 따라 어떤 $k$를 사용해서 길이 $2^k$짜리 두개의 구간으로 나눠야 하는지 미리 계산해둔 배열입니다. ST 배열은 Sparse Table 자료구조의 본체인데, pair의 첫 원소에는 level 값이 들어가고, 두번째 원소에는 그 level을 가지는 노드 번호가 저장됩니다.
int pw2[LOGN], lg2[MAXN*2];
pair<int,int> ST[LOGN][MAXN*2];
void sparsetable_build(){
// calculate pw2 array
pw2[0] = 1;
for(int k=1;k<LOGN;k++) pw2[k] = pw2[k-1] * 2;
// calculate lg2 array
memset(lg2, -1, sizeof lg2);
for(int k=0;k<LOGN;k++) if( pw2[k] < MAXN*2 ) lg2[pw2[k]] = k;
for(int i=1;i<MAXN*2;i++) if( lg2[i] == -1 ) lg2[i] = lg2[i-1];
// calculate sparse table
for(int i=1;i<=2*N-1;i++) ST[0][i] = {lev[euler[i]], euler[i]};
for(int k=1;k<LOGN;k++){
for(int i=1;i<=2*N-1;i++){
if( i + pw2[k-1] > 2*N-1 ) continue;
ST[k][i] = min(ST[k-1][i], ST[k-1][i+pw2[k-1]]);
}
}
}
두 노드를 받아서 LCA를 리턴하는 함수를 구현합시다. 위에서 계산해 놓은 lg2, pw2 배열을 활용하면 깔끔한 구현이 가능합니다. l,r은 각각 노드 u,v가 Euler Tour에서 나타나는 위치입니다. 노드가 여러번 등장하더라도 존재하더라도 아무 위치나 하나 선택하면 됩니다.
int LCA(int u, int v){
int l = idx[u][0], r = idx[v][0];
if( l > r ) swap(l,r);
int k = lg2[r-l+1];
return min(ST[k][l], ST[k][r-pw2[k]+1]).second;
}
마지막으로 입출력을 받는 main 함수를 구현합시다. dfs를 통해 Euler Tour, level배열 등을 먼저 채워준 뒤 Sparse Table을 구축해야 한다는 점에 유의합시다. 또한 당연하게도, LCA함수를 호출하기 전에 이러한 전처리 과정들이 모두 끝나 있어야 합니다.
int main(){
scanf("%d",&N);
for(int i=0;i<N-1;i++){
int a,b; scanf("%d%d",&a,&b);
E[a].push_back(b); E[b].push_back(a);
}
dfs(1,-1,0);
sparsetable_build();
scanf("%d",&Q);
while( Q-- ){
int u,v; scanf("%d%d",&u,&v);
printf("%d\n",LCA(u,v));
}
}
전체 합쳐진 코드는 링크 에서 확인할 수 있습니다.