Graph, SCC and BCC
목차
개요
이 포스트를 쓰며
DFS Numbering에 대한 많은 재미있는 사실들이 있다. 최근에 고급 알고리즘이라는 과목을 들으면서 DFS에서 Numbering을 할때 가지는 자체적인 성질과 그에 관련된 알고리즘들을 공부하게 되었다. SCC와 BCC가 그런것들이다. 이들은 PS에서 매우 유용하게 쓰일 수 있으며, 다양한 상황에 적용할 수 있고, 알아두는 것만으로 풀 수 있는 문제영역이 넓어진다. 또한 DFS Numbering 자체가 구현 자체가 쉬우므로 보통 Dynamic Programming 이나, 2-SAT등 다양한 테크닉과 섞어 쓴다는 점을 유의하여 관련 문제들을 추려보았다.
DFS
혹여라도 DFS에 대해 잘 모르는 사람을 위해 DFS에 대한 간단한 설명을 한다면, DFS는 그래프의 탐색 방법중 하나로서 재귀함수를 통한 재귀적인 방법을 통하여 방문하는, 좀 더 쉽게 말하면, 일단 방문 가능한 지점을 발견하면 방문하고 그 다음 방문할 지점을 찾는 방법을 뜻한다. 전에 설명한 Tree DP와 유사하지만, 이번엔 Directed Graph 에서의 설명이 주가 될것이므로 그에 대한 Pseudo Code를 제공하겠다.
visit = Array
E = Adjacency_List
dfs(u):
visit[u] = 1
for v in E(u):
if visit[v]
continue
else
dfs(v)
매우 짧고 간결한 것을 볼 수 있다. 이 코드를 기반으로 수많은 알고리즘을 해결 할 수 있음을 밑에서 보일 것이다.
간단한 원리
일단 DFS Numbering은 Pre Number와 Post Number두가지로 나뉘어진다. Pre Number는 후술할 Tree에서 Sub-Tree 관계, 및 BCC 구축등에서 유용하게 쓰이고, Post Number는 SCC, Topological Sort를 할때 유용하게 쓰인다. Pre Number는 함수 호출이 발생하기 전, 즉, 최초로 함수에 진입한 시점에 Numbering을 하는것이고 Post Order는 모든 함수호출이 끝난 뒤, 즉, 함수가 끝날 때 Numbering을 하는 것이다. 이를 Pseudo Code 로 나타내면 다음과 같다.
number = 0
pre = Array
post = Array
visit = Array
V = Vertex_List
E(x) = Adjacency_List
dfs(u):
number += 1
pre[u] = number
visit[u] = 1
for v in E(u):
if visit[v]
continue
else
dfs(v)
number += 1
post[u] = number
numbring(V):
for u in V:
if visit[u] == 1
continue;
else
dfs(u);
이 코드를 변형함으로서 다양한 문제를 해결 할 수 있으며, 이 코드 자체만으로 풀리는 문제가 있으니 뒤에서 다양한 원리들을 설명하겠다.
개념
DFS Tree
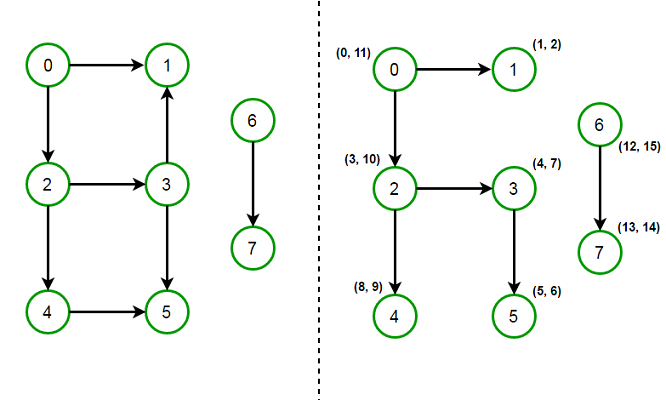
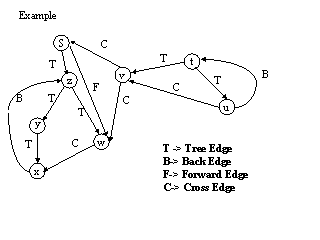
정말 빼놓을 수 없는 개념이 있는데, 그것은 바로 DFS Tree 이다. DFS를 진행할 때 사용한 간선만(정점을 방문할 때 사용한 간선) 남기고 사용하지 않은 간선을 제거하면 Tree, 상황에 따라서는 Forest가 만들어질것이다. 이때 만들어지는 Tree를 DFS Tree 라고 한다. 위의 그림이 DFS Tree가 만들어지는 좋은 예시이다. 이때, 여기서 중요한 개념들이 있다. 바로 Forward Edge와, Back Edge와, Cross Edge와, Tree Edge이다. 가장 먼저 Tree Edge는 위에서 말했던 DFS를 진행할 때, 사용한 간선들을 의미한다. 그 다음은 Back Edge인데, 어떤 정점에서 자신의 Ancestor로 향하는, 사용되지 않은 간선을 의미한다. 그 다음은 Forward Edge가 있는데, 이는 어떤 정점에서 자신의 Descendant로 향하는 Edge를 의미한다. 마지막은 Cross Edge인데, 저것중 그 무엇도 속하지 않는 edge를 의미한다. 즉, 두 정점의 LCA(부모를 타고가다 만나는 최초의 공통 조상)를 기준으로 부트리를 만들었을 때, 부트리간 이동하는 정점을 의미하게 된다. 이 정의들을 잘 숙지 해 두면 다양한 상황에서 응용할 수 있다.
Cycle Detect
어떤 Graph에서 Cycle이 존재하는지 검사하는 방법은 생각보다 간단하다. Back Edge의 존재 여부만 판단하면 되기 때문이다. 이것은 매우 자명한 사실인데, 어떤 조상 노드에서 해당 노드로 내려오다가 Back Edge를 발견해서 올라가면 결국 그것이 Cycle이 된다.
Back Edge가 존재하면 그 Graph는 Cycle을 가지고 있다.
여기서의 Psuedo Code는 다음과 같다.
number = 0
pre = Array
post = Array
visit = Array
V = Vertex_List
E(x) = Adjacency_List
hasCycle = False
dfs(u):
number += 1
pre[u] = number
visit[u] = 1
for v in E(u):
if visit[v]
if(post[v] == 0)
hasCycle = True
continue
else
dfs(v)
number += 1
post[u] = number
numbring(V):
for u in V:
if visit[u] == 1
continue;
else
dfs(u);
중요한 점은 아직 Post Order가 0인 지점이면서 방문한 지점일때만 hasCycle을 True로 바꿔준다는 것인데, 이는 Cross Edge혹은 Forward Edge와 구분짓기 위함이다. Forward Edge와 Cross Edge Detect는 어떻게 할까? 이것은 Pre Number를 이용하면 된다. Pre Number가 나보다 작으면서, Post Number가 존재한다면 Cross Edge 임은 자명하다. 그리고 Pre Number가 나보다 크다면 Forward Edge인 것 역시 자명하다. 이는 위, Pseudo Code 에서 조금만 추가하면 되므로 굳이 언급하지는 않겠다.
Topological Sort
Topological Sort는 그래프가 DAG(Directed Acyclic Graph, 사이클이 없는 방향 그래프)라는 조건하에 In-Degree(나로 향하는 Edge의 개수)가 0인 정점을 지워나가면서 모든 정점을 지웠을때의, 지워진 순서를 나열하는 것을 의미한다. 이를 2중 for문으로 구현하면 $O(N^{2})$ 이라는 시간 복잡도를 지니며, Queue 자료구조로 해결하려 하면 $O(N)$ 에 해결할 수 있지만, 구현이 자체가 복잡해진다. 그렇다면 이를 쉽게 구현하는 방법은 무엇일까? 그것은 바로 Post Number를 기준으로 내림차순 정렬을 하는 것이다.
Post Number 기준으로 내림차순 정렬을 하면 Topological Sort가 된다.
이 성질을 증명하는 방법은 다음과 같다. 먼저 함수 방문이 발생하면 해당하는 자식 노드보다 나의 Post Number가 더 크다는건 자명하다. 이 에 따라, 어떤 정점 $u, v$ 가 존재하고, $v$의 Post Number가 $u$의 Post Number보다 작다면, 둘은 서로다른 부트리에 속하거나, $u$가 $v$의 조상임은 위에서 정리에 따라 자명하다. 즉, 서로 다른 부트리에 속해있다면 LCA를 카운팅 한 시점에서 Cross Edge가 존재하지 않는다면, 순서는 상관 없으므로 내림차순 정렬에 영향을 안받는다. 하지만 이때, Cross Edge가 존재하면서 Post Order가 나보다 작은 경우가 존재할 수 있을까? 이는 존재할 수 없다. 만약 그렇게 된다면 자신은 자식또는 후손이 되어야 하므로 Cross Edge 정의에 위배된다. 따라서 공통 조상을 전부 카운팅 했다면 Post Number의 크기에 따라 자연스럽게 정렬이 된다. 마지막으로, 조상이었다면 당연히 큰것을 먼저 출력하므로, 내림차순으로 출력하게 되면 자동으로 Topological Sort가 된다. 이에 대한 Pseudo Code는 구현하기 쉬우므로 굳이 추가하지는 않겠다. 추가적인 개념 설명을 하자면, In-Degree가 0인 정점을 Source, Out-Degree가 0인 정점을 Sink라고 한다. 이것을 꼭 기억해두자.
Strongly Connected Components
매우 중요한 개념이며, Graph를 Decomposition 할때 많이 사용된다. 어떤 방향 그래프가 Strongly Connected 되어 있다는 건, 임의의 두 정점 $(u, v)$ 쌍에 대해서 $u$ 에서 $v$로 항하는 경로가 항상 존재하는 상태를 의미하게 된다. 이때 Strongly Connected Components는 어떤 방향그래프 $G$에 대해 정점들을 Strongly Connected한 정점끼리 분할 할 수 있는가를 묻는 것이다.
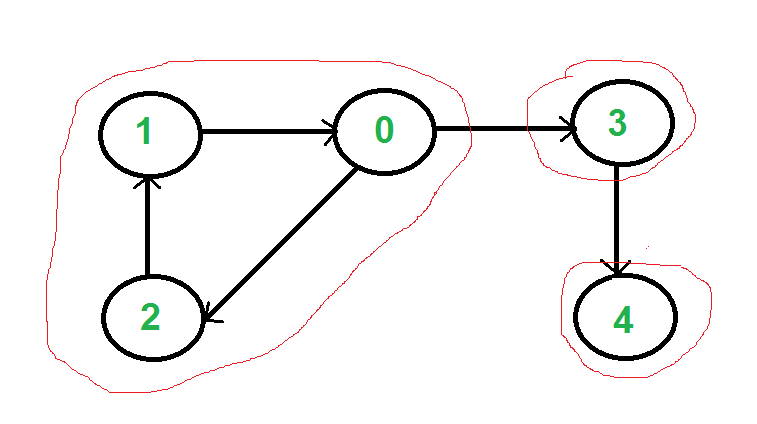
여기까지 봤으면 감이 왔을 것이다. 그렇다면 Strongly Connected Components를 효율적으로 발견하는 알고리즘이 있는가에 대해 궁금할 것이다. 이제 소개할 것은 Cosaraju Algorithm 이다. 이제부터 줄여서 SCC라고 부르겠다. SCC를 전부 찾고 난 다음 위에 그림 처럼 새로운 그래프로 구축해보자. 이렇게 새로이 구축된 그래프는 DAG임은 자명하다. 이러한 그래프 에서 Sink Node에 속하는 정점을 하나 발견해서 거기서 DFS건 BFS건 Flood Fill(방문 가능한 모든 정점을 보는것)을 시행하고 난 뒤에, 방문된 지점을 하나의 SCC로 묶고, 방문되지 않은 지점 중, 그 다음 Sink를 찾아서 다시 하나의 SCC로 묶는다면 이것은 쉽게 해결될 것이다. 문제는 이 그래프의 원본이 DAG가 아니므로 Topological Sort의 방법으로 Sink를 찾을 수가 없다는 것이다. 하지만 과연 그럴까?
모든 방향 그래프에서 Post Number가 가장 큰 것이 SCC로 재구축한 그래프의 Source에 속한다.
Sink는 보장할 수 없지만 위의 성질은 만족한다. 생각해보면 간단한 게, 자신과 연결된 모든 지점을 탐색하고 나서 자신으로 돌아왔을 때, 자신의 Post Number가 가장 크다면, Source 임은 매우 자명한 성질이기 때문이다. 두번째 성질이다.
모든 방향 그래프에서 정점 $x$의 Post Number를 $Pt(x)$ 라고 할 때, $Pt(u) > Pt(v)$를 만족하면 $u$와 $v$는 같은 SCC에 속하거나, 그렇지 않다면 두 정점 사이에 경로가 없거나 있더라도 $u$에서 $v$로 가는 경로만 존재한다.
이 두번째 성질이 가장 중요하다. 우선 같은 SCC에 속하는건 Flood Fill을 수행하는 순서에 지장이 없으므로 무시한다. 그리고 이에 대한 증명은 나보다 Post Number가 작으면서 SCC에 속하는 1->2->3->1 의 Cycle을 예시로 들어주면 증명할 수 있다. 제일 중요한 속하지 않을 때, 경로가 없거나 $u$에서 $v$로 가는 경로만 존재한다는 것을 증명하자면, $u$에서 $v$로 가능 경로가 없는 것은 1->2->3, 4->5 에서 1과 4를 예시로 들면 된다. 이후 마지막으로 $u$에서 $v$가는 경로가 있을때, $v$의 자신을 포함한, 조상으로 가는 Back Edge가 존재하게 된다면 이는 곧 SCC가 되므로 SCC가 아니면서 $u$ 에서 $v$, $v$에서 $u$로 가는 경우는 존재할 수 없음은 자명하다.
자 이 두가지 성질을 어떻게 응용하면 될까? 바로 역그래프를 그리는 것이다. 모든 간선을 반대로 뒤집어주어서 새로운 그래프를 만들고 역그래프에서 Post Number를 매겨준다. 이후 제일 큰 것부터 다시 원래 그래프에서 Flood Fill을 수행하면 SCC를 구할 수 있다. 이것이 어떻게 가능한 걸까?
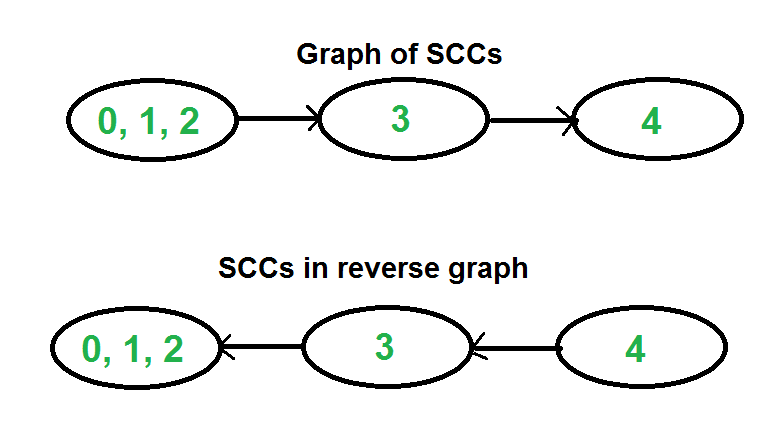
위의 두 성질을 응용하면 첫번째 성질로 인해, 역그래프에서의 Soruce를 구할 수 있다. 하지만 이는 원래 그래프에서 Sink 임은 매우 자명하다. 그리고, 두번째 성질로 인하여, SCC간의 Topological Sort를 이루게 된다. 이를 Pseudo Code로 구현하면 다음과 같다.
scc_number = 0
number = 0
pre = Array
post = Array
visit = Array
visit_scc = Array
V = Vertex_List
E(x) = Adjacency_List
ER(x) = Adjacency_List
SCC(x) = SCC_List
bucket = Array
flood(u):
visit_scc[u] = scc_number
scc_number += 1
for v in E(u):
if visit_scc[v]
continue
else
flood(v)
dfs(u):
number += 1
pre[u] = number
visit[u] = 1
for v in ER(u):
if visit[v]
continue
else
dfs(v)
number += 1
post[u] = number
bucket[number] = u
numbring(V):
for u in V:
if visit[u] == 1
continue;
else
dfs(u);
main():
V <- input
E <- input
for u in V:
for v in E(u):
u push into Er[v]
numbering(V);
for u in 2 * |V| to 1:
if (scc_visit[u])
continue
else
scc_number += 1
flood(u)
이런식으로 DFS 두번만으로 해결 할 수 있다.
Biconnected Components
지금까지는 Directed Graph에서의 성질을 설명하였고, 이번엔 Bi-directed Graph, 즉, 무방향 그래프에서의 성질을 설명하고자 한다. 무방향 그래프에서는 SCC라는 개념이 존재할 수 없는데, 어떤 두 정점에 간선이 있는 시점에서 그 두 정점은 서로 오갈수 있으므로 항상 Strongly Connected 하다. 따라서 무방향 그래프에서는 다른 개념이 적용된다. 먼저 Bridge와 Separating Vertex이다. 그 단어들에서 느껴지듯이 어떤 edge가 단절되면 두개의 서로 연결되지 않은 그래프로 나누어지는 edge를 의미한다. Separating Vertex는 어떤 정점을 지웠을 때, 두개 이상의 서로 연결되지 않은 그래프로 나누어지는 vertex를 의미한다. 좀 더 엄밀하게 정의 내려야 하지만, 이 정도 수준에서만 이해 할 수 있으면 될것 같다. BCC의 정의를 미처 설명을 못했는데 정의는 다음과 같다. 무슨 정점을 지워도 연결 관계가 끊기지 않는, 즉, Connected 되어있는 Component를 의미한다. 즉, BCC는 Vertex의 집합이 아닌 Edge의 집합임을 알 수 있다. 그렇다면 이러한 BCC들 간에 연결을 끊어주는데 핵심 역할을 하는것이, Separating Vertex 이다. Bridge는 당연하게도 Edge가 단 하나만 존재하는 경우가 Bridge가 된다. 그러면 먼저, 무방향 그래프에서의 DFS Tree를 구축하는 것을 알아야 하는데, 그것은 다음과 같다.
먼저, 직계 부모는 Back Edge로 취급하지 않고 방향 그래프에서의 DFS를 수행하듯이 같은 방법으로 수행시켜주면 되는것이다. 이러한 방법으로 구해진 DFS Tree 에는 Cross Edge와 Foward가 존재하지 않는다. 즉, Back Edge만 존재한다.
그다음 알아야 할것은 Separating Vertex가 가지는 성질이다.
DFS Tree 내부에서 Root Node는 자식이 둘 이상이면 Separting Vertex 이다.
이는 증명하기 쉽다. 우선 DFS Tree 내부에서 Root로 향하는 Back Edge가 몇개가 있더라도 의미는 없다. 자식이 하나면 본인이 사라져도 그래프는 모두 연결되어 있기 때문이다. 하지만, 자식이 둘 이상이라면 항상 Separating Vertex이다. 이는 Cross Edge가 존재하지 않는다는 점을 생각해보면 자명하다.
DFS Tree 내부에서 Root Node가 아닌 다른 Node는 자신을 제외한 자식중에 그 자식의 자신을 포함한 Descendant에서 자신을 제외한 Ancestor로 향하는 Back Edge가 없는 자식이 하나라도 있다면 Separating Vertex이다.
이도 생각해보면 자명하다. 자신을 제외한 Ancestor로 향하는 Back Edge가 있다면 그 Descendant에 해당하는 BCC 그룹이 만들어질 것이고, 그것에 자연히 해당 Vertex가 속하게 될것이다. 하지만 만약에 그러한 Back Edge가 없는 자식이 하나라도 존재한다면 당연하게도 두개 이상의 단절된 그래프가 만들어 질것이고, 곧 그것은 그 Vertex가 Separating Vertex임을 의미한다.
이제 이 성질을 이용하여 Bridge, Separating Vertex, BCC 까지 모두 구하는 알고리즘을 보여줄 것이다. 우선 $low$ 배열이란게 있다고 하자. 우선 DFS Tree 상에서 일단 기본적으로 $low[u] = pre[u]$이다.(여기서 $pre[u]$는 $u$의 Pre Number) 이때 자신의 자식노드로 향하는 Tree Edge $(u, v)$이라면 $low[u] = min(low[u], low[v])$ 로 구하게 된다. 하지만 Back Edge라면 $low[u] = min(low[u], pre[v])$가 된다. 이는 생각해보면 간단한 것이, Back Edge의 경우 조상노드의 Pre Number 중 제일 작은것을 고르게 하면 된다. 그리고 Tree Edge를 통하여 자손이 가진 $low$ 정보를 통해 내 자손이 가지고 있던 Back Edge중 제일 작은 Pre Number를 찾는 것이다. 그러면 이제 Tree Edge $(u, v)$에 대해서 $pre[u] <= low[v]$ 라면 루트 노드를 제외하고 해당 노드는 항상 Separating Vertex가 되는것이다. 이제 여기서 Stack을 이용하여 Tree Edge와 Back Edge를 저장하면서 다니면 BCC역시 마저 구할 수 있다. 이때, Edge가 단 하나인 BCC는 언제나 Bridge임을 기억하면 모든 걸 다 구할 수 있게 되었다.
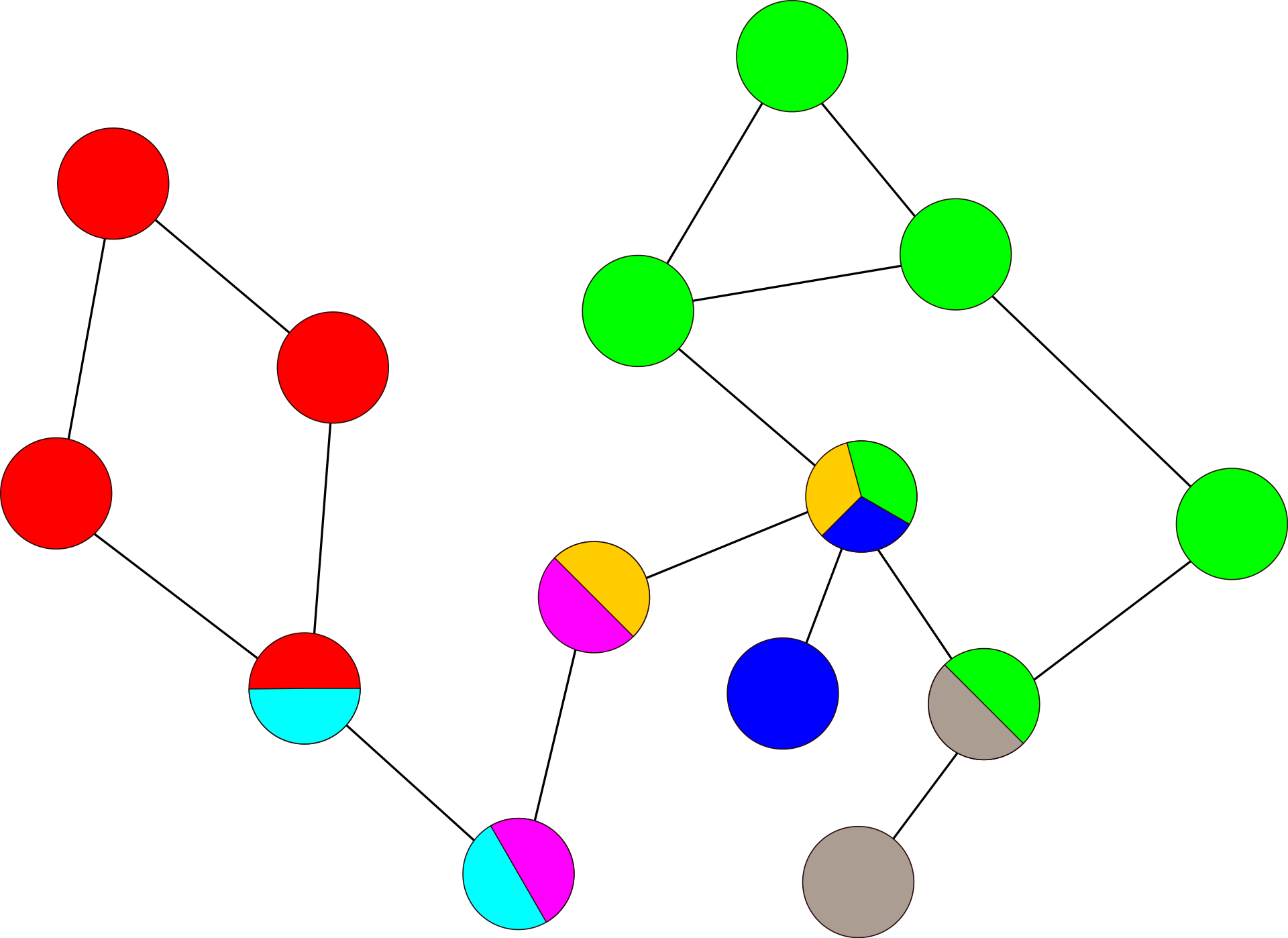
추가적으로 위의 그림을 보면 알 수 있겠지만, BCC와 Separating Vertex만으로 구성한 그래프는 항상 트리이다.
아래는 BCC, Separating Vertex, Bridge를 모두 구하는 Pseudo Code 이다.
bcc_count = 0
BCC(i) = List
low = array
pre = array
pre_cnt = 0
separating_vertex = List
edge_stack = Stack
Edge(x) = Adjacency List
dfs(u, par):
child = 0
flag = False
pre_cnt = pre_cnt + 1
low[u] = pre[u] = pre_cnt
for v in Edge(u):
if (v == par and pre[v] != 0)
continue;
else if(pre[v] == 0) #Tree Edge
child += 1
push (u, v) into edge_stack
dfs(v, u)
low[u] = min(low[u], low[v])
if (pre[u] <= low[v])
bcc_count += 1
flag = True
while (top of edge_stack != (u, v))
top of edge_stack push into BCC(bcc_count)
pop from edge_stack
pop from edge_stack
(u, v) push into BCC(bcc_count)
else if(pre[u] > pre[v]) #Back Edge
push (u, v) into edge_stack
low[u] = min(low[u], low[v]);
if(par == -1 and child >= 2)
push u into separating_vertex
if(par != -1 and flag)
push u into Separating_vertex
Sub-Tree
이 장은 사실 크게 다룰 게 없다. 그냥 성질만 이야기 하고 끝낼것이다. 무방향 그래프, 그중에서도 트리에서 Pre Number는 꽤 가치가 있는데 그것은 바로 자신의 Sub Tree에 해당하는 Vertex 들이 연속적으로 놓여있음을 알 수 있기 때문이다. 이는 성질중 하나일 뿐이므로 문제 풀이때 자세히 설명하겠다.
구현
위의 pseudo code 들을 C++로 구현한 코드이다.
#include <cstdio>
#include <algorithm>
#include <vector>
#include <stack>
#include <set>
using namespace std;
vector<int> edge[2510];
int bcc_cnt = 0;
vector<pair<int, int> > bcce[5010];
vector<int> sep;
int pre_cnt = 0;
int pre[2510], low[2510];
stack<pair<int, int> > st;
void dfs(int u, int par) {
int child = 0, flag = 0;
low[u] = pre[u] = ++pre_cnt;
for(int i = 0; i < edge[u].size(); i++) {
int v = edge[u][i];
if(pre[v] && v == par) continue;
if(!pre[v]) {
child++;
st.push({u, v});
dfs(v, u);
low[u] = min(low[u], low[v]);
if(pre[u] <= low[v]) {
bcc_cnt++;
flag = 1;
while(st.size() && (st.top().first != u || st.top().second != v)) {
bcce[bcc_cnt].push_back(st.top());
bccc[st.top().first].insert(bcc_cnt);
bccc[st.top().second].insert(bcc_cnt);
st.pop();
}
if(st.size()) {
bcce[bcc_cnt].push_back(st.top());
bccc[st.top().first].insert(bcc_cnt);
bccc[st.top().second].insert(bcc_cnt);
st.pop();
}
}
}
else if(pre[u] > pre[v]) {
st.push({u, v});
low[u] = min(low[u], pre[v]);
}
}
if(child >= 2 && par == -1) sep.push_back(u);
else if(flag && par != -1) sep.push_back(u);
}
BCC를 구현한 것이며 위에서 모두 설명한 것 이므로 넘어가도록 한다.
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> e[10010], er[10010];
int num = 0, pre[10010], post[10010];
int p[20010];
int cnt = 0;
vector<int> scc[10010];
int visit[10010];
void dfs(int u) {
if(visit[u]) return;
scc[cnt].push_back(u);
visit[u] = cnt;
for(auto v : e[u]) dfs(v);
}
void ordering(int u) {
if(pre[u]) return;
pre[u] = ++num;
for(auto v : er[u]) ordering(v);
post[u] = ++num;
p[num] = u;
}
int main() {
int n, m;
scanf("%d %d",&n,&m);
for(int i = 0; i < m; i++) {
int x, y;
scanf("%d %d",&x,&y);
e[x].push_back(y);
er[y].push_back(x);
}
for(int i = 1; i <= n; i++) ordering(i);
for(int i = 2 * n; i >= 1; i--) {
if(!p[i]) continue;
if(visit[p[i]]) continue;
cnt++;
dfs(p[i]);
}
return 0;
}
SCC를 구현한 것이며 마찬가지로 넘어가도록 한다.
SCC, BCC 모두 DFS 한 두번이 전부 이므로 시간복잡도는 $O(V + E)$이다.
문제풀이
줄 세우기
이 링크를 통해 문제를 볼 수 있다. 이 문제는 아이들의 키의 대소비교 관계가 주어지면 아이들을 키순으로 세우는 문제이다. 그냥 대놓고 위상정렬 문제라고 되어있다. 풀이는 간단하다 그냥 DFS를 수행한 뒤, Post Number가 큰 순으로 정렬하면 끝나는 문제이다.
코드는 아래와 같다.
시간 복잡도는 $O(n + m)$이다.
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> o[32010];
int pre[32010], post[32010];
bool cmp(int a, int b) {
return post[a] > post[b];
}
int cnt = 0;
void dfs(int u) {
if(pre[u]) return;
pre[u] = ++cnt;
for(auto &v : o[u]) dfs(v);
post[u] = ++cnt;
}
int ans[32010];
int indegree[32000];
int main() {
int n, m;
scanf("%d %d", &n, &m);
for(int i = 0; i < m; i++) {
int x, y;
scanf("%d %d", &x, &y);
o[x].push_back(y);
}
for(int i = 1; i <= n; i++) {
ans[i - 1] = i;
dfs(i);
}
sort(ans, ans + n, cmp);
for(int i = 0; i < n; i++) printf("%d ",ans[i]);
printf("\n");
return 0;
}
Strongly Connect Component
이 링크를 통하여 문제를 볼 수 있다. 간단하다. SCC를 구하여라. 대신에 조심할 것은 오름차순 정렬하는 것 정도만 조심하면 된다.
시간 복잡도는 $O(n + m)$ 이다.
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> e[10010], er[10010];
int num = 0, pre[10010], post[10010];
int p[20010];
int cnt = 0;
vector<int> scc[10010];
int visit[10010];
void dfs(int u) {
if(visit[u]) return;
scc[cnt].push_back(u);
visit[u] = cnt;
for(auto v : e[u]) dfs(v);
}
void ordering(int u) {
if(pre[u]) return;
pre[u] = ++num;
for(auto v : er[u]) ordering(v);
post[u] = ++num;
p[num] = u;
}
int order_i[10010];
bool cmp(const int &a, const int &b) {
return scc[a][0] < scc[b][0];
}
int main() {
int n, m;
scanf("%d %d",&n,&m);
for(int i = 0; i < m; i++) {
int x, y;
scanf("%d %d",&x,&y);
e[x].push_back(y);
er[y].push_back(x);
}
for(int i = 1; i <= n; i++) ordering(i);
for(int i = 20000; i >= 1; i--) {
if(!p[i]) continue;
if(visit[p[i]]) continue;
cnt++;
dfs(p[i]);
sort(scc[cnt].begin(), scc[cnt].end());
}
for(int i = 1; i <= cnt; i++) order_i[i - 1] = i;
sort(order_i, order_i + cnt, cmp);
printf("%d\n",cnt);
for(int i = 0; i < cnt; i++) {
int x = order_i[i];
for(auto v : scc[x]) printf("%d ", v);
printf("-1\n");
}
return 0;
}
텀 프로젝트
이 링크를 통하여 문제를 볼 수 있다. 이 문제는 Cycle을 Detect 하는 것 뿐만, 아니라 그 Cycle에 속하는 학생들을 팀으로 묶는 문제이다. 단, Loop가 존재하므로 유의하면서 풀어야 한다. 재밌는 점은, 모든 vertex가 단 하나의 Edge 만을 가진다는 것인데, 이 경우에는 복잡한 형태의 SCC는 존재할 수 없고 오직 Ring 형태, 즉, 고리 모양의 Cycle만 존재한다는 것이다. 이를 응용하면, Cycle을 Detect함과 동시에 stack에 vertex를 넣어두다가 빼주면서 팀을 만들어 주면 된다.
시간 복잡도는 $O(n)$ 이다.
#include <cstdio>
#include <vector>
#include <stack>
using namespace std;
int n;
int number = 0;
int pre[100010];
int post[100010];
int team[100010];
vector<int> e[100010];
vector<int> st;
void dfs(int u) {
st.push_back(u);
pre[u] = ++number;
for(auto &v : e[u]) {
if(pre[v]) {
if(!post[v]) {
for(int i = (int)st.size() - 1; i >= 0; i--) {
team[st[i]] = 1;
if(st[i] == v) break;
}
}
continue;
}
else dfs(v);
}
post[u] = ++number;
}
void numbering(int n) {
for(int i = 1; i <= n; i++) {
if(pre[i]) continue;
dfs(i);
}
}
int main() {
int t;
scanf("%d",&t);
while(t--) {
scanf("%d",&n);
for(int i = 1; i <= n; i++) {
pre[i] = post[i] = team[i] = 0;
e[i].clear();
}
for(int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
e[i].push_back(x);
}
numbering(n);
int ans = 0;
for(int i = 1; i <= n; i++) ans += !team[i];
printf("%d\n",ans);
}
return 0;
}
Museums Tour
이 링크를 통하여 문제를 볼 수 있다. 이 문제는 어떤 도시들이 있는데 각 도시엔 박물관이 하나씩 있고, 열리는 날이 매 주에 몇개씩 정해져 있다. 이때 이 나라는 날짜 방식이 특이해서 한주가 50일이 될 수 도 있고, 7일이 될 수 도 있다. 이때, 출발 도시는 항상 1이며, 항상 0일 부터 시작한다. 이때, 각 도시를 여행하는데에는 도로를 쓰며 그 도로를 지나는데 정확히 1일이 소요된다. 이때, 박물관 투어 진행자는 도로를 이동할 지, 여행을 마감할지 그 도시에 도착할 때 정할 수 있다.(박물관이 열려있으면 보고 마감할 수 있다.)이때, 최대한 서로다른 박물관을 몇개 볼 수 있는지 구하는 게 이 문제의 핵심이다. 일단 이 문제는 다음과 같이 변형할 수 있다. 현재 도시가 $u$, 날짜를 $t$라고 한다면, 다음 도시 $v$로 이동한다면 $(u, t) to (v, t + 1)$ 로 나타낼 수 있다. 이는 edge 관계 하나이며, 이를 SCC로 묶어내면 그 묶음 내에서 어떤 $(u, t)$가 박물관이 열리는 시점이라면 $u$의 박물관을 본다고 할 때, 서로 다른 볼 수 있는 박물관의 개수를 각 SCC에 구할 수 있다. 그리고 나서, 각 SCC를 새로운 그래프로 구축해서 $(1, 0)$을 포함하는 SCC에서 부터 Topological Sort를 사용하여 DP로 해결 하면 쉽게 풀 수 있다. 하지만 이는 $O(nd)$ 라는 무식하게 큰 메모리 공간을 수용하지 못한다. 따라서 발상을 전환 해야하는데, 생각해보면 $t$를 배제한 $(u, v)$ 관계 만으로 구축한 SCC 내부에서 $dp[u][t]$의 상태공간을 만든 뒤, 맨처음 설명한 $(u, t) to (v, t + 1)$관계를 Flood Fill 하듯이 채워넣으면 굳이 맨 처음 Edge로 새로운 그래프를 구성하지 않더라도 문제를 해결 할 수 있다. 아래는 이 문제의 풀이이다.
시간 복잡도는 $O(nd)$ 이다.
#include <cstdio>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <list>
using namespace std;
int d;
int p[100010][50];
stack<int> rnode;
vector<int> e[100010], er[100010];
int rvisit[100010];
int sw = 0;
void rdfs(int u) {
if(rvisit[u]) return;
rvisit[u] = 1;
for(auto v : er[u]) rdfs(v);
rnode.push(u);
}
int cnt = 0;
int num[100010];
vector<int> scc[100010];
int sum[100010][51], dp[100010][51], chk[100010][51], use[100010];
int degree[100010];
void dfs(int u) {
if(num[u]) return;
num[u] = cnt;
scc[cnt].push_back(u);
for(auto v : e[u]) dfs(v);
}
int main() {
int n, m;
scanf("%d %d %d", &n, &m, &d);
for(int i = 0; i < m; i++) {
int x, y;
scanf("%d %d", &x, &y);
e[x].push_back(y);
er[y].push_back(x);
}
for(int i = 1; i <= n; i++) {
for(int j = 0; j < d; j++) {
scanf("%1d",&p[i][j]);
}
}
for(int i = 1; i <= n; i++) {
if(rvisit[i]) continue;
rdfs(i);
}
while(rnode.size()) {
int u = rnode.top();
rnode.pop();
if(num[u]) continue;
cnt++;
dfs(u);
}
queue<int> q;
q.push(num[1]);
while(q.size()) {
int u = q.front();
q.pop();
for(auto &s : scc[u]) {
for(auto &t : e[s]) {
int v = num[t];
if(u == v) continue;
degree[v]++;
if(degree[v] > 1) continue;
q.push(v);
}
}
}
int ans = 0;
q.push(num[1]);
dp[1][0] = 1;
int cnm = 0;
while(q.size()) {
int u = q.front();
q.pop();
for(auto &s : scc[u]) {
for(int j = 0; j < d; j++) {
if(chk[s][j]) continue;
list<pair<int, int> > nd;
queue<pair<int, int> > dq;
chk[s][j] = ++cnm;
dq.push( { s, j } );
int maxd = 0;
while(dq.size()) {
pair<int, int> x = dq.front();
dq.pop();
nd.push_back(x);
if(maxd < dp[x.first][x.second]) maxd = dp[x.first][x.second];
for(auto &t : e[x.first]) {
int v = num[t];
int k = (x.second + 1) % d;
if(chk[t][k]) continue;
if(u != v) continue;
chk[t][k] = cnm;
dq.push( {t, k} );
}
}
if(maxd == 0) continue;
for(auto &x : nd) {
if(!p[x.first][x.second] || use[x.first] == cnm) continue;
use[x.first] = cnm;
maxd++;
}
for(auto &x : nd) dp[x.first][x.second] = maxd;
if(maxd > ans) ans = maxd;
}
}
for(auto &s : scc[u]) {
for(auto &t : e[s]) {
int v = num[t];
if(u == v) continue;
if(--degree[v] == 0) q.push(v);
for(int i = 0; i < d; i++) dp[t][(i + 1) % d] = max(dp[t][(i + 1) % d], dp[s][i]);
}
}
}
printf("%d\n",ans - 1);
return 0;
}
자동차 공장
이 링크를 통하여 문제를 확인할 수 있다. 이 문제는 DFS Numbering 을 활용한 문제이다. 간단하게 말하면 직급 체계가 Tree모양으로 되어있고, p a x 가 주어지면, a의 부하의 월급에 x를 더해주고 u a 가 주어지면 a의 월급을 출력하는 문제이다. 이 문제는 위에서 언급한 Post Number를 배제한 Pre Number가 부트리에 대해 연속성을 띈다는 점을 응용한 문제이다. 간단하게 생각하면 Pre Number를 매기면서 Last Sub Tree Number 역시 매겨준다. 즉, 내 자식들의 Last Sub Tree Number가 제일 큰것을 고르는 것이다. 만약 자식이 없다면 Pre Number는 Last Sub Tree Number가 된다. 그리고 이것들을 기억해 두었다가 Lazy Propagation 이나 BIT를 트리키하게 변형한 방법으로 월급을 조절하면 쉽게 해결 할 수 있다.
시간 복잡도는 $O(N log N)$이다.
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
struct bung {
int lazy;
int hap;
}tr[4100000];
int order[610000];
int subt[610000];
int wage[610000];
vector<int> son[610000];
void update_lazy(int d) {
if (d == 0) return;
update_lazy(d >> 1);
int l = d << 1;
int r = l + 1;
int tmp = tr[d].lazy;
tr[d].lazy = 0;
tr[l].lazy += tmp;
tr[l].hap += tmp;
tr[r].lazy += tmp;
tr[r].hap += tmp;
}
void update(int st, int ed, int cst) {
if (st > ed) return;
while (1) {
if (st == ed) {
tr[st].hap += cst;
tr[st].lazy += cst;
break;
}
if (st & 1) {
tr[st].hap += cst;
tr[st].lazy += cst;
st++;
}
if (!(ed & 1)) {
tr[ed].hap += cst;
tr[ed].lazy += cst;
ed--;
}
if (st > ed) break;
st >>= 1;
ed >>= 1;
}
}
struct node {
int f;
int pos;
int max1;
};
vector<node> stk;
void dfs(int u) {
int cnt = 0;
int i;
int tmp;
node now, sav;
now.f = 0;
now.pos = u;
while (1) {
if (order[now.pos] == 0) {
order[now.pos] = ++cnt;
now.max1 = cnt;
}
tmp = 0;
for (i=now.f;i<son[now.pos].size();i++) {
tmp = son[now.pos][i];
if (order[tmp] != 0) continue;
break;
}
now.f = i + 1;
if (i == son[now.pos].size()) {
subt[now.pos] = now.max1;
if (stk.size() == 0) break;
sav = stk.back();
if (sav.max1 < now.max1) sav.max1 = now.max1;
now = sav;
stk.pop_back();
}
else {
stk.push_back(now);
now.f = 0;
now.pos = son[now.pos][i];
now.max1 = 0;
}
}
}
int main() {
int i;
int k;
int n, q;
int x, y;
char qt[3];
scanf("%d %d",&n,&q);
for(k=1;k<n;k<<=1);
scanf("%d",&wage[1]);
for (i=2;i<=n;i++) {
scanf("%d %d",&wage[i], &y);
son[y].push_back(i);
}
dfs(1);
for (i=1;i<=n;i++) tr[k+order[i]-1].hap = wage[i];
for (i=0;i<q;i++) {
scanf("%s",qt);
if (qt[0] == 'p') {
scanf("%d %d",&x,&y);
update(k + order[x], k + subt[x] - 1, y);
}
else {
scanf("%d",&x);
update_lazy((k+order[x]-1) >> 1);
printf("%d\n",tr[k+order[x]-1].hap);
}
}
return 0;
}
반드시 가는 곳
이 링크를 통하여 문제를 볼 수 있다. 이 문제는 격자상의 좌표계에서 시작점, 출발점, 장애물이 주어졌을 때, 항상 방문해야 하는 점을 출력하는 문제이다. 이 문제는 BCC로 매우 쉽게 해결 할 수 있는데 방법은 다음과 같다. BCC를 새롭게 구축한 뒤, BCC 파트에서 언급한 트리를 만든 뒤, 해당 경로로 이동 하였을 때, 방문하는 Separating Vertex를 조사하면 된다. 그것은 매우 자명한데, Separating Vertex 이외의 다른 점을 들러서 해당 경로로 이동할 방법이 없기 때문이다.
시간 복잡도는 $O(n^{2})$ 이다.
#include <cstdio>
#include <algorithm>
#include <vector>
#include <stack>
#include <set>
using namespace std;
char o[52][52];
vector<int> edge[2510];
int bcc_cnt = 0;
set<int> bccc[5010];
vector<pair<int, int> > bcce[5010];
vector<int> n_edge[5010];
vector<int> sep;
int num = 0;
int pre[2510], low[2510];
stack<pair<int, int> > st;
void dfs(int u, int par) {
int cnt = 0, flag = 0;
low[u] = pre[u] = ++num;
for(int i = 0; i < edge[u].size(); i++) {
int v = edge[u][i];
if(pre[v] && v == par) continue;
if(!pre[v]) {
st.push({u, v});
dfs(v, u);
low[u] = min(low[u], low[v]);
if(pre[u] <= low[v]) {
bcc_cnt++;
flag = 1;
while(st.size() && (st.top().first != u || st.top().second != v)) {
bcce[bcc_cnt].push_back(st.top());
bccc[st.top().first].insert(bcc_cnt);
bccc[st.top().second].insert(bcc_cnt);
st.pop();
}
if(st.size()) {
bcce[bcc_cnt].push_back(st.top());
bccc[st.top().first].insert(bcc_cnt);
bccc[st.top().second].insert(bcc_cnt);
st.pop();
}
}
cnt++;
}
else if(pre[u] > pre[v]) {
st.push({u, v});
low[u] = min(low[u], pre[v]);
}
}
if(cnt >= 2 && par == -1) sep.push_back(u);
else if(flag && par != -1) sep.push_back(u);
}
int visit[5010];
vector<int> trace;
void find_path(int u, int t, int n) {
visit[u] = 1;
trace.push_back(u);
if(u == t) {
for(int i = 0; i < trace.size(); i++) {
int v = trace[i];
if(v > bcc_cnt) {
int x = v - bcc_cnt - 1;
if(o[x/n][x%n] == '.') o[x / n][x % n] = 'o';
}
}
}
for(int i = 0; i < n_edge[u].size(); i++) {
int v = n_edge[u][i];
if(visit[v]) continue;
find_path(v, t, n);
}
trace.pop_back();
}
int main() {
int dx[2] = {1, 0};
int dy[2] = {0, 1};
int n;
scanf("%d",&n);
for(int i = 0; i < n; i++) scanf("%s",o[i]);
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(o[i][j] != '#') {
for(int k = 0; k < 2; k++) {
int nx = i + dx[k];
int ny = j + dy[k];
if(nx >= n || ny >= n) continue;
if(o[nx][ny] == '#') continue;
edge[i * n + j].push_back(nx * n + ny);
edge[nx * n + ny].push_back(i * n + j);
}
}
}
}
for(int i = 0; i < n * n; i++) {
if(pre[i]) continue;
dfs(i, -1);
}
for(int i = 0; i < sep.size(); i++) {
int u = sep[i];
for(set<int>::iterator x = bccc[u].begin(); x != bccc[u].end(); x++) {
n_edge[bcc_cnt + u + 1].push_back(*x);
n_edge[*x].push_back(bcc_cnt + u + 1);
}
}
int s = -1, t = -1;
int s_pos = -1, t_pos = -1;
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(o[i][j] == 'S') {
s = i * n + j;
for(int i = 0; i < sep.size(); i++) {
int v = sep[i];
if(s == v) {
s_pos = v + bcc_cnt + 1;
break;
}
}
if(s_pos != -1) continue;
for(int k = 1; k <= bcc_cnt; k++) {
for(int i = 0; i < bcce[k].size(); i++) {
pair<int, int> v = bcce[k][i];
if(v.first == s) s_pos = k;
if(v.second == s) s_pos = k;
}
}
}
if(o[i][j] == 'E') {
t = i * n + j;
for(int i = 0; i < sep.size(); i++) {
int v = sep[i];
if(t == v) {
t_pos = v + bcc_cnt + 1;
break;
}
}
if(t_pos != -1) continue;
for(int k = 1; k <= bcc_cnt; k++) {
for(int i = 0; i < bcce[k].size(); i++) {
pair<int, int> v = bcce[k][i];
if(v.first == t) t_pos = k;
if(v.second == t) t_pos = k;
}
}
}
}
}
find_path(s_pos, t_pos, n);
for(int i = 0; i < n; i++) printf("%s\n", o[i]);
return 0;
}
마무리
이 포스트를 통하여 다양한 Graph 문제를 해결하는데 사람들이 도움이 되었으면 한다. 또한 Graph에 좀더 관심을 가지고 그에 관련된 각종 알고리즘에 관심을 가지는 계기가 되었으면 좋겠다.
참고자료
- geeksforgeeks.org; Strongly Connected Components. Geeks for Geeks
- www.techiedelight.com; Arrival and Departure Time of Vertices in DFS. Techie Delight
- users.cis.fiu.edu; Graph Algorithms – Depth First Search and it’s application in Decomposition of Graphs. Dr. Giri Narasimhan
- geeksforgeeks.org; Biconnected Components. Geeks for Geeks
- en.wikipedia.org; Graph-Biconnected-Components. Zyqqh