April 10, 2019 13:56

개요

정렬(Sorting)은 알고리즘 문제 풀이뿐 아니라, 어떤 분야의 프로그래밍을 하면서도 수없이 마주치는 문제입니다. 일반적으로 정렬에 대해 공부할 때는 $O(N^2)$이지만 기본 개념을 설명하기 위해 배우는 버블 정렬(Bubble sort), 삽입 정렬(Insertion sort), 선택 정렬(Selection sort) 등과, 보다 효율적으로 $O(NlogN)$ 시간에 해결해주는 퀵정렬(Quicksort), 병합 정렬(Merge sort), 힙정렬(Heapsort), 그리고 비교 기반이 아닌 자릿수(digit) 기반으로 $O(N)$에 해결하는 기수 정렬(Radix sort), 카운팅 정렬(Counting sort) 정도를 배우게 됩니다.

굉장히 많은 종류의 정렬을 배운 것 같지만, 정렬에 대해 더 깊이 파고 들어가보면 이 정도는 아주 기본적인 것들에 불과하다는 것을 알 수 있습니다. 실제로 이 알고리즘들을 배운 그대로 코드로 구현한 것은 실생활의 데이터와는 잘 맞지 않는 경우도 있고(예: 퀵정렬을 평범하게 구현하면 최악의 경우, 단순히 이미 정렬이나 역정렬된 데이터에서 $O(N^2)$이 되는 것 등), 수의 범위가 작은 경우 끝까지 $O(NlogN)$의 로직을 고집하지 않고 $O(N^2)$의 정렬을 사용하는 것이 더 효율적인 경우도 있습니다.

이 글에서는 일반적으로 정렬을 공부할 때는 배우지 않는 특수한 정렬들이 어떤 것들이 있는지 알아보고 각 알고리즘의 특징을 알아보도록 하겠습니다.

Introsort

위에서도 잠깐 언급했지만, 단순한 퀵정렬은 최악의 경우 $O(N^2)$의 시간복잡도를 가집니다. 피벗을 $lo$로 잡으나, $hi$로 잡으나 정렬할 데이터가 이미 정렬 혹은 역정렬이 되어 있는 경우 항상 피벗이 한쪽으로 쏠리게 되므로, $O(N)$개의 원소를 피벗 기준으로 나누는 작업을 $O(N)$번 수행하여 $O(N^2)$이 됩니다. 피벗을 가운데로 잡는다고 해도, 모든 원소가 전부 동일한 케이스이고 같은 원소에 대해 옮길 방향이 정해져 있다면 역시 $O(N^2)$이 됩니다.

하지만 퀵소트라는 이름에서도 나타나듯이, 퀵소트 자체는 평균적인 경우의 퍼포먼스가 매우 좋은 편입니다. 퀵소트의 장점을 완전히 버리기에는 아까우므로, 최악의 케이스에도 대응할 수 있는 대안 중 하나로 나타난 것이 Introsort입니다.

Introsort는 기본적으로 퀵정렬 + 힙정렬로 구성된 하이브리드 정렬입니다. 알고리즘의 의사코드는 다음과 같습니다.¹

procedure sort(A : array):
    let maxdepth = ⌊log(length(A))⌋ × 2
    introsort(A, maxdepth)

procedure introsort(A, maxdepth):
    n ← length(A)
    p ← partition(A)  // assume this function does pivot selection, p is the final position of the pivot
    if n ≤ 1:
        return  // base case
    else if maxdepth = 0:
        heapsort(A)
    else:
        introsort(A[0:p], maxdepth - 1)
        introsort(A[p+1:n], maxdepth - 1)

전체적인 흐름은 퀵정렬과 같으나, maxdepth라는 변수를 하나 더 가지고 있다는 점이 다릅니다. maxdepth는 introsort함수가 재귀호출할 최대 깊이를 설정하여, 이 깊이 이상으로 재귀가 들어갈 경우 데이터가 편향되어 있을 가능성이 높으므로, 재귀를 더 들어가지 않고 남은 부분에 대해서는 일반적으로 상수는 조금 크지만 항상 $O(NlogN)$이 보장되는 힙정렬을 수행합니다.

처음에 maxdepth를 설정하는 부분에서 로그값에 곱해지는 상수는 예측되는 데이터의 상태에 따라 적절하게 바꿀 수 있지만, maxdepth를 점근적으로 로그보다 큰 값을 설정하면 $O(NlogN)$을 보장할 수 없게 됩니다.

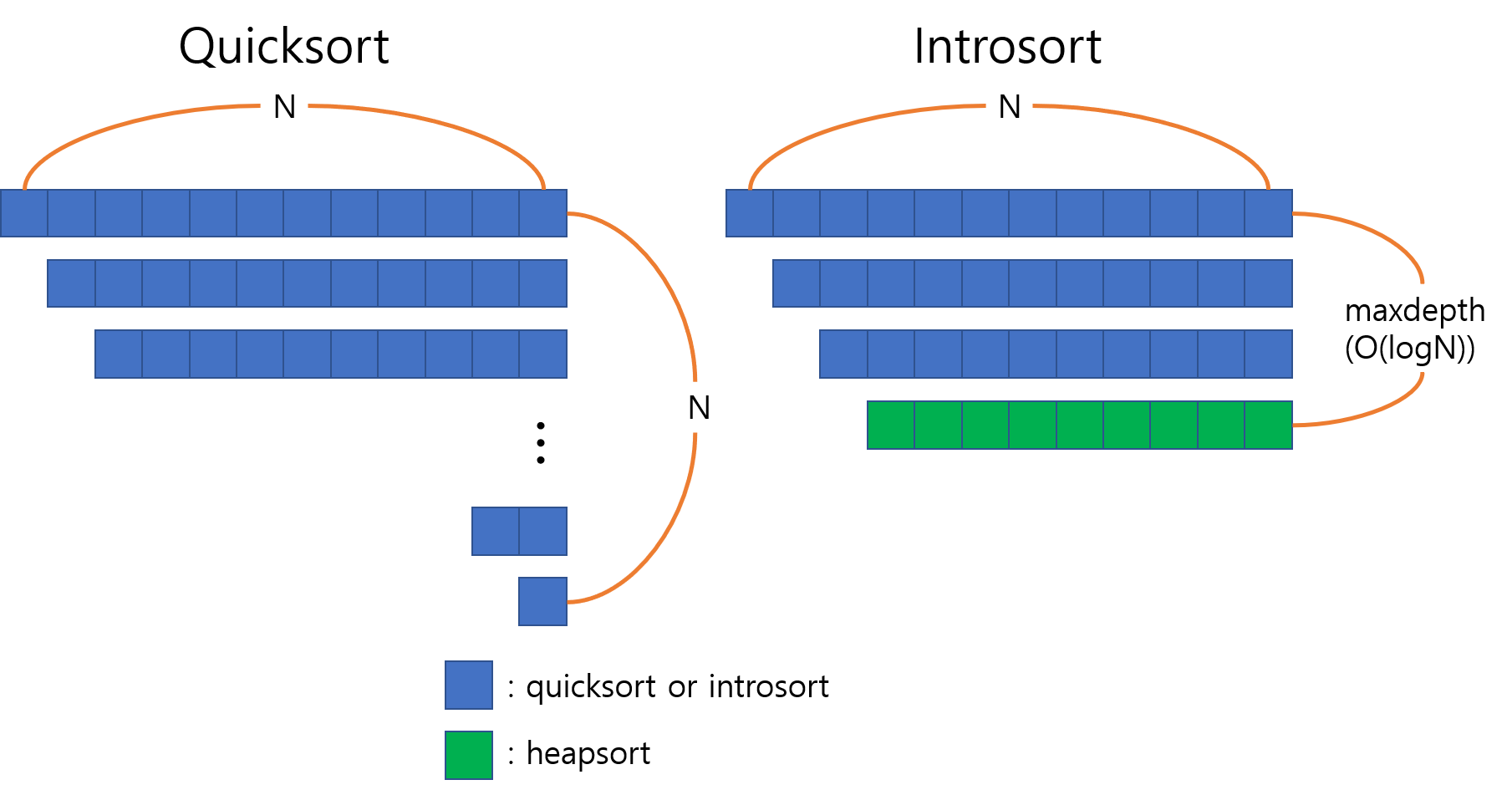
GCC의 std::sort는 introsort의 변형된 버전을 사용합니다. 작은 범위의 원소들에 대해서는 굳이 상수가 큰 $O(NlogN)$ 정렬을 사용하는 것보다 상수가 작은 $O(N^2)$ 정렬을 사용하는 편이 더 빠르기 때문에, 16개 미만의 원소들에 대해서는 일단 무시하고 진행한 뒤 마지막에 전체에 대해 삽입 정렬을 수행하는 방법을 선택합니다.

Timsort

Introsort가 이론적인 최악의 경우를 대비해 변형시킨 알고리즘이라면, Timsort는 현실에서 있을 법한 다양한 데이터들에 대해 최적화를 시킨 알고리즘입니다. 기본적으로는 병합 정렬과 삽입 정렬의 하이브리드이며, 최악의 경우 $O(NlogN)$을 보장할 뿐 아니라 최선의 경우 $O(N)$에 수행도 가능한데다가 stable²한 속성까지 갖춘 똑똑한 알고리즘이라고 할 수 있습니다. 실제로 Timsort는 Python 2.3부터 기본 정렬 알고리즘으로 사용되고 있으며, 이후 Java 등 많은 라이브러리에서 표준 정렬로 채택했습니다.

반면에 똑똑한만큼 구현 자체는 길고 복잡한 편이고, 최적화를 위해 쓰이는 테크닉도 특이합니다. 2개 이상의 연속된 원소가 non-descending하거나 strictly descending한 것들을 ‘run’이라는 단위로 묶고, 이들에 대한 정보를 스택에 쌓아 32~64 사이의 값을 가지는 ‘minrun’ 크기까지 삽입 정렬로 정렬한 뒤, 그 ‘minrun’들을 다시 merge해나가면서 전체를 정렬하는 방식을 사용합니다.

복잡한 방식을 택하고 있지만 랜덤 데이터에 대해서는 다른 보통의 $O(NlogN)$ 정렬과 퍼포먼스에서는 거의 차이가 없습니다. 그러나 현실에서는 데이터의 일부가 이미 정렬되어있거나 대략적으로 정렬된 경향을 보이는 경우가 많기 때문에, 이미 정렬된 부분에 대한 연산 횟수를 줄였다는 점에서 매우 실용적인 알고리즘이라고 할 수 있습니다.

Binary Insertion Sort

BInary insertion sort는 기존의 삽입 정렬에서 비교 횟수를 최소화한 정렬입니다. 사실 독립적인 알고리즘이라기보다는 삽입 정렬을 보완한 것에 가깝습니다. $i$번째 원소까지가 정렬되어 있다면 $i+1$번째 원소를 넣을 위치는 $1$ ~ $i+1$ 사이에서 이분 탐색으로 찾을 수 있으므로, $i$번째부터 하나씩 비교하면서 내려가는 것이 총 $O(N)$ 번의 비교를 요구하는 것에 비해서 비교 횟수를 $O(logN)$ 번으로 줄일 수 있습니다. 다만 위치는 이분 탐색으로 찾더라도 그 이후의 원소들을 전부 한 칸씩 뒤로 밀어야 하는 것에는 변함이 없으므로 총 시간복잡도는 $O(N^2)$이 유지됩니다. 비교 연산의 비용이 크고 원소를 옮기는 연산의 비용이 작은 환경에서 유용할 수 있는 알고리즘입니다.

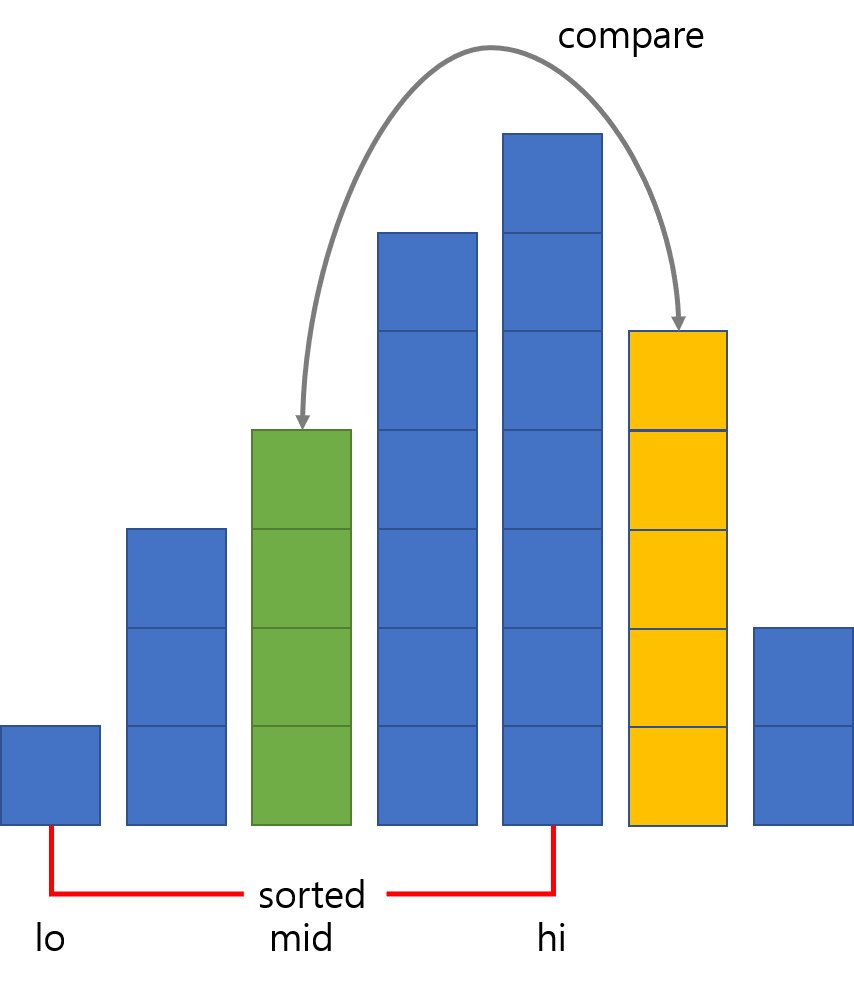
다섯 개의 막대가 정렬된 상태에서, 여섯 번째 막대(노란색)를 삽입하는 과정입니다. 먼저 정렬된 구간 전체에서 가운데 막대인 3번째 원소와 비교하고,

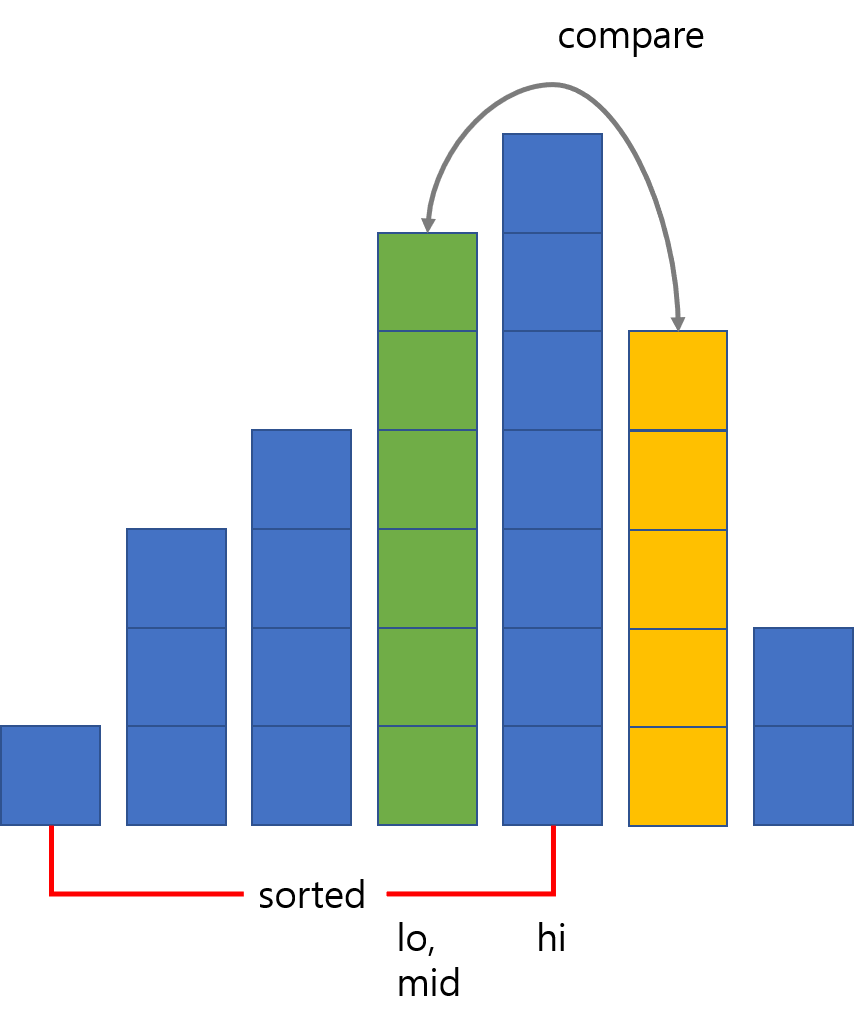
6번째 막대가 더 크니 lo를 위로 올리고 다시 가운데 막대인 4번째 막대와 비교합니다.

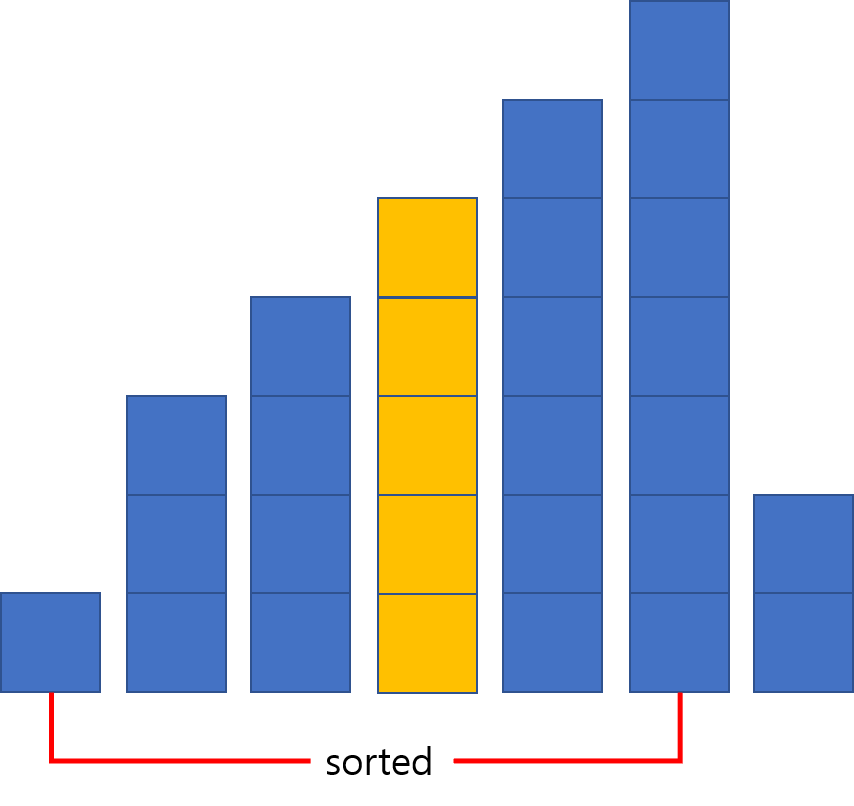
4번째 원소가 더 크니, 노란 막대가 들어가야 할 자리는 4번째임을 알 수 있고, 기존의 4, 5번째 막대는 뒤로 한 칸씩 밀고 노란 막대를 4번째 자리에 넣습니다.

Shell sort

Shell sort는 삽입 정렬과 버블 정렬의 개념(교환, 삽입)을 활용한 알고리즘입니다. 어떤 큰 gap에서 시작해서, 매 루프마다 각 원소에 대해 원소가 삽입될 대략적인 위치를 gap만큼씩 건너뛰며 교환해나가고, 그 gap을 점차적으로 줄여나가며 모든 원소가 정렬될 때까지 보는 방식입니다.

의사 코드는 다음과 같습니다.³

# Sort an array a[0...n-1].
gaps = [701, 301, 132, 57, 23, 10, 4, 1]

# Start with the largest gap and work down to a gap of 1
foreach (gap in gaps)
{
    # Do a gapped insertion sort for this gap size.
    # The first gap elements a[0..gap-1] are already in gapped order
    # keep adding one more element until the entire array is gap sorted
    for (i = gap; i < n; i += 1)
    {
        # add a[i] to the elements that have been gap sorted
        # save a[i] in temp and make a hole at position i
        temp = a[i]
        # shift earlier gap-sorted elements up until the correct location for a[i] is found
        for (j = i; j >= gap and a[j - gap] > temp; j -= gap)
        {
            a[j] = a[j - gap]
        }
        # put temp (the original a[i]) in its correct location
        a[j] = temp
    }
}

gap만큼 떨어진 원소가 현재 원소보다 더 큰 동안 계속해서 들어가는 방식은 삽입 정렬과 유사하지만, 이 위치가 주변의 다른 원소들에 대해서도 완전히 정렬되어있다는 보장은 없기 때문에, ‘확률적으로 정렬에 가까운’ 위치를 찾았다고 볼 수 있습니다.

예를 들어 gap이 2일 때 원소가 삽입될 위치를 찾는 과정을 표현하면 다음과 같습니다.

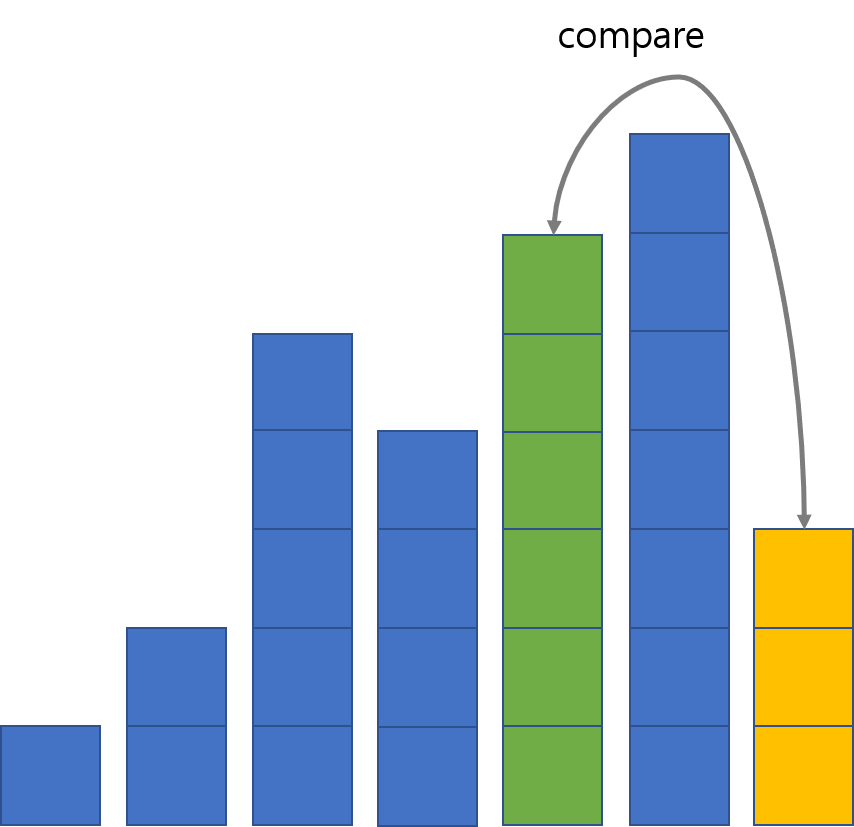
노란 막대에서 gap만큼, 즉 2만큼 떨어져 있는 막대인 초록 막대를 봅니다. 노란 막대가 더 작으므로 둘을 교환합니다.

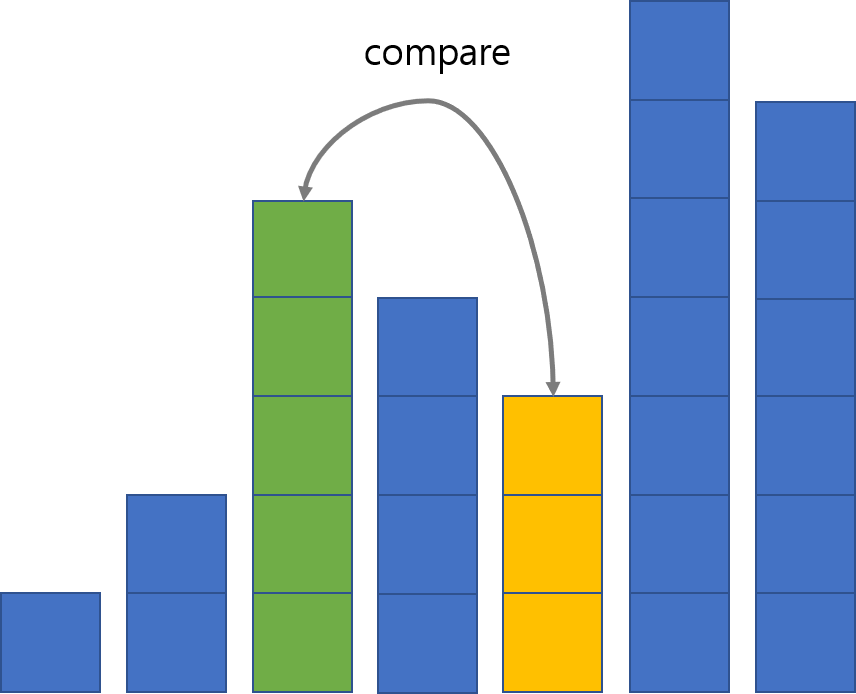
다시 노란 막대에서 2만큼 떨어져 있는 막대인 초록 막대를 보니 또 노란 막대가 작습니다. 둘을 교환합니다.

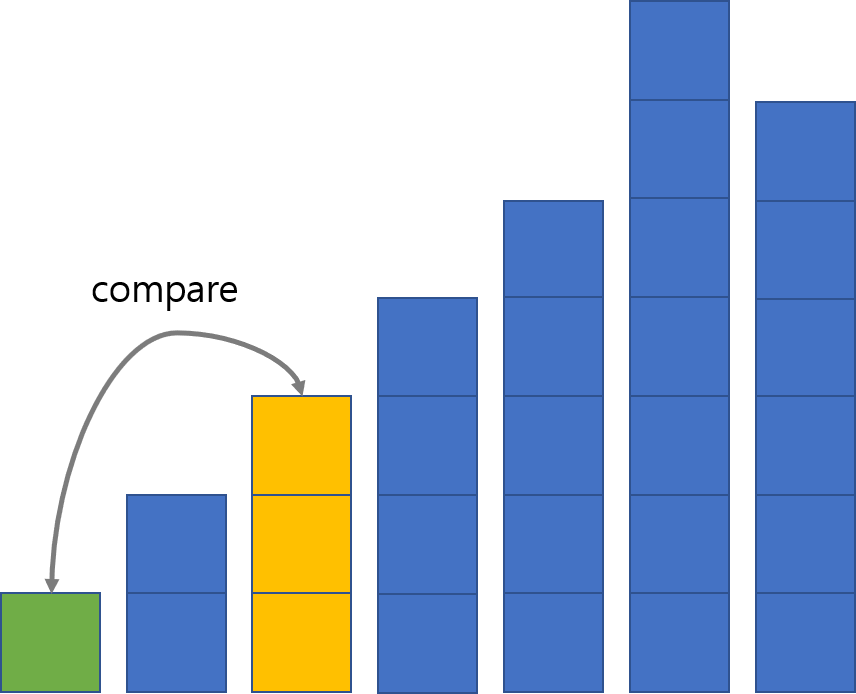
이번에는 노란 막대가 더 크니 노란 막대를 삽입하는 과정을 중단합니다.

Shell sort에서 가장 중요한 것은 이 gap을 어떤 방법으로 정하느냐입니다. gap을 정하는 방법에 따라 최악의 경우 시간복잡도 자체가 변하기 때문입니다. Shell sort를 처음으로 고안한 Shell이 제시했던 $N/2$, $N/4$, …, $1$로 gap을 설정하는 방법은 최악의 경우 시간복잡도가 $Θ(N^2)$이고, $2^p3^q$ 꼴로 나타낸 수들로 설정하면 $Θ(Nlog^2N)$, 또는 어떤 정수열들을 사용하면 $O(N^{4/3})$과 같은 특이한 최악의 경우 시간복잡도도 나오게 됩니다. 다만 Shell sort는 대부분의 경우 평균 $O(NlogN)$의 시간복잡도를 가지고, 대체로 정렬된 데이터에 대해 더 높은 효율을 보이기 때문에 실생활의 데이터에 대해 유용한 경우가 많이 있을 수 있다는 점이 장점입니다.

Cycle Sort

Cycle sort는 쓰기 연산을 최소화하는 알고리즘입니다. 전체적으로는 큰 득이 없어보이고 대부분의 컴퓨터에서는 웬만한 $O(N^2)$ 정렬보다 더 느리지만, 추가 메모리를 $O(1)$만 사용해야 하면서도 쓰기 연산이 극도로 비싼 경우, 예를 들면 EEPROM과 같이 쓰기 연산이 메모리의 수명을 단축시키는 경우에 좋을 수 있습니다. 의사 코드는 다음과 같습니다.⁴

# Sort an array in place and return the number of writes.
def cycleSort(array):
  writes = 0

  # Loop through the array to find cycles to rotate.
  for cycleStart in range(0, len(array) - 1):
    item = array[cycleStart]

    # Find where to put the item.
    pos = cycleStart
    for i in range(cycleStart + 1, len(array)):
      if array[i] < item:
        pos += 1

    # If the item is already there, this is not a cycle.
    if pos == cycleStart:
      continue

    # Otherwise, put the item there or right after any duplicates.
    while item == array[pos]:
      pos += 1
    array[pos], item = item, array[pos]
    writes += 1

    # Rotate the rest of the cycle.
    while pos != cycleStart:

      # Find where to put the item.
      pos = cycleStart
      for i in range(cycleStart + 1, len(array)):
        if array[i] < item:
          pos += 1

      # Put the item there or right after any duplicates.
      while item == array[pos]:
        pos += 1
      array[pos], item = item, array[pos]
      writes += 1

  return writes

전체적인 알고리즘은 전체 원소가 정렬될 때까지, 남아있는 부분에서 현재 원소보다 작은 원소의 개수를 세서 현재 원소가 들어가야 할 정확한 위치를 단번에 찾는 방식입니다. 그렇기 때문에 교환이 많아야 $N-1$번만 일어나고, 한 번 자기 자리에 들어간 원소는 절대로 다시 움직이지 않기 때문에 평균적으로도 선택 정렬에 비해 더 적은 쓰기 연산이 들어갑니다.

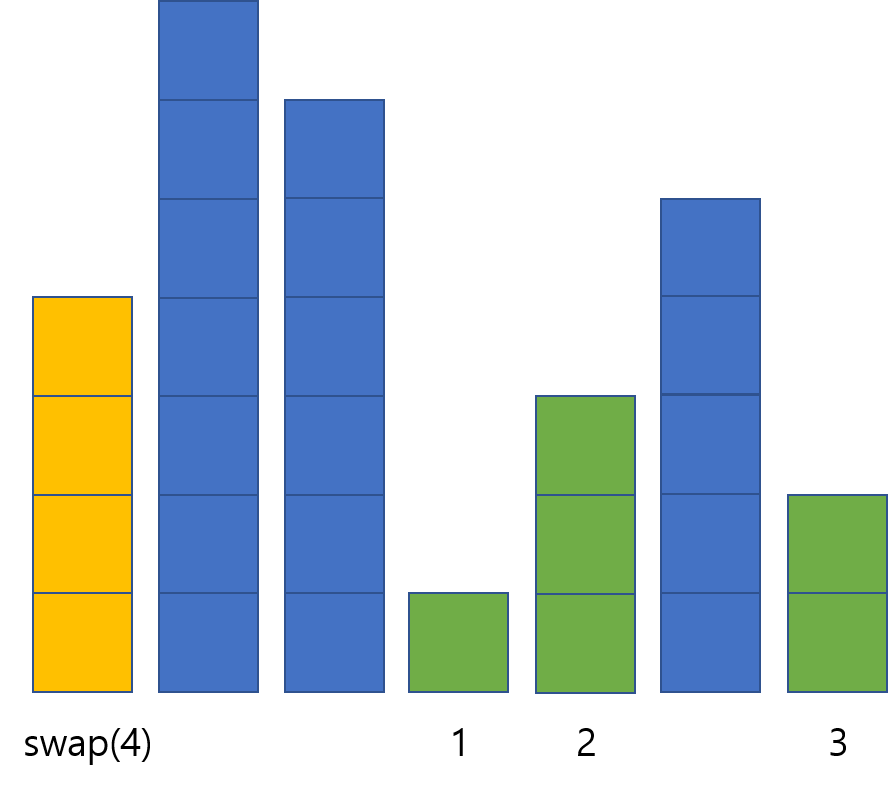
이와 같이 노란색 막대보다 더 작은 막대가 세 개가 있으므로 노란색 막대는 네 번째 자리에 들어가야 한다는 것을 알 수 있습니다. 노란색 막대를 네 번째 자리에 있는 막대와 교환해줍니다.

Bitonic Sort

Bitonic sort는 병렬적인 실행 환경에서 효율적으로 정렬하기 위한 알고리즘입니다. 단일 스레드로 수행하면 $O(Nlog^2N)$으로 오히려 일반적인 $O(NlogN)$ 정렬들에 비해 효율성이 떨어지지만, 프로세서가 무수히 많은 환경에서는 $O(log^2N)$에 정렬을 할 수 있습니다. Bitonic이라 함은 수열이 중간의 어떤 원소를 기점으로 그 이전까지는 증가하고, 그 이후로는 감소하는 형태를 의미합니다. 파이썬으로 로직을 구현한 코드는 다음과 같습니다..⁵

def bitonic_sort(up, x):
    if len(x) <= 1:
        return x
    else:
        first = bitonic_sort(True, x[:len(x) // 2])
        second = bitonic_sort(False, x[len(x) // 2:])
        return bitonic_merge(up, first + second)

def bitonic_merge(up, x):
    # assume input x is bitonic, and sorted list is returned
    if len(x) == 1:
        return x
    else:
        bitonic_compare(up, x)
        first = bitonic_merge(up, x[:len(x) // 2])
        second = bitonic_merge(up, x[len(x) // 2:])
        return first + second

def bitonic_compare(up, x):
    dist = len(x) // 2
    for i in range(dist):  
        if (x[i] > x[i + dist]) == up:
          x[i], x[i + dist] = x[i + dist], x[i] #swap

이 코드는 단일 스레드를 기준으로 하고 있지만, 병렬적인 처리를 위해서는 bitonic_sort 함수와 bitonic_merge 함수의 실행 및 비교할 때의 루프 등이 모두 여러 스레드에서 병렬적으로 실행되어야 합니다. 정렬이 수행되는 과정을 대략적인 그림으로 표현하면 다음과 같습니다.⁶

복잡해 보이지만, 기본적인 원리는 일반적인 병합 정렬과 비슷합니다. 다만, 일반적인 merge 과정은 해당 원소 개수 전체를 하나의 스레드가 전부 확인하는 방법밖에 없어 아무리 많은 프로세서가 있더라도 $O(N)$ 미만으로 단축시킬 수 없는 데에 비해, bitonic sort에서는 이 그림에서 세로로 나란한 빨간 상자들에 속한 연산들끼리 모두 병렬적으로 처리를 할 수 있기 때문에 프로세서가 많다면 $1$부터 $logN$까지의 합, 즉 $O(log^2N)$ 시간에 정렬이 가능합니다.

마치며

지금까지 다양한 종류의 정렬에 대해 살펴보았지만, 이것들은 실제로 지금까지 만들어진 정렬 알고리즘의 수에 비하면 새발의 피에 불과합니다. 알고리즘 종류도 셀 수 없이 많고, 목적도 가지각색입니다. 심지어는 실용성은 전혀 없이 그저 재미로만 만들어진 알고리즘, 일부러 느리게 만든 알고리즘 등도 존재합니다. 예를 들면 ‘바보정렬’이라는 뜻을 가진 Bogosort는 매우 유명한 ‘비효율적인 정렬 알고리즘’ 중 하나로, 단순히 원소 전체를 섞고 정렬이 잘 되었는지 확인하기를 정렬이 될 때까지 반복하며 시간복잡도는 $O((N+1)!)$입니다. 그의 변형본도 Gorosort, Bogobogosort, Bozosort, Worstsort 등 여럿 존재합니다.

다른 예시로 Slowsort는 병합 정렬과 비슷하지만 양쪽을 정렬한 뒤 merge를 하는 대신 양쪽의 최댓값 중 더 큰 값을 그 구간의 가장 오른쪽에 놓고, 나머지 원소들에 대해 다시 재귀를 호출하는 방식으로 이루어져 지수 꼴의 복잡도를 가집니다. 컴퓨터 공학에서 자주 쓰이는 용어인 divide-and-conquer를 패러디한 multiply-and-surrender 기법을 내세우고 있습니다.

또한 퀵정렬과 같은 익히 알려진 알고리즘에도 피벗을 어떻게 선택하느냐에 따라서 수십 가지 변형이 있고 각각의 특징이 다르며, 배열로 표현된 자료구조와 링크드 리스트로 표현된 자료구조에서도 알고리즘의 동작이 달라질 수 있는 등, 정렬이라는 기초적인 주제 하나를 가지고도 탐구할 수 있는 주제는 이렇게 무수히 많습니다. 이 글을 통해 단순해 보이는 작업인 정렬 하나만으로도 얼마나 많은 연구를 할 수 있는지 독자 분들이 느낌을 받을 수 있었으면 좋겠습니다.

참고하면 좋은 자료

• http://panthema.net/2013/sound-of-sorting/ : 다양한 정렬 함수들의 수행 과정을 그림과 소리로 동시에 ‘느낄’ 수 있게 해주는 프로그램입니다.
• https://www.youtube.com/watch?v=8oJS1BMKE64&list=PLZh3kxyHrVp_AcOanN_jpuQbcMVdXbqei : 위 프로그램의 실행 과정을 영상으로 만든 것들입니다.