그래프 색칠과 NP-Completeness
서론
현실의 여러 대상들은 그래프로 추상화 할 수 있다. 그래프를 색칠하는 것은, 서로 인접한 두 정점이 같은 색을 같지 않도록 색칠 하는 것이다. 이 그래프를 색칠하는 문제는, 다양한 스케쥴링 문제 혹은 컴파일러의 레지스터 배치, 패턴 매칭, 시험/수업 시간표 작성 등 다양한 문제를 해결할 수 있다. 이런 문제들이 다항시간안에 검증이 가능하지만, 다항 시간안에 풀리는지는 밝혀지지 않는 NP-Complete 문제라는 것을 알아보자.
그래프
그래프는, 정점을 나타내는 집합 $V$와, 간선을 나타내는 집합 $E$의 원소인, $G = (V, E)$로 나타낸다. 정점은 임의의 원소이다. 즉, 숫자나 그래프 정점의 붙여진 글자, 도시 이름 등 아무것이나 될 수 있다. (엄밀히 말하면, $2^{2^V} \cap 2^V \cap V = \phi$ 여야 하고, 이는 정점과 후에 설명한 간선의 오해를 피하기 위함이다.) 간선은, 크기 2인 $V$의 부분집합이다. ${u, v} \in E$ 일 경우, 우리는 정점 $u$와 정점 $v$가 인접해있다고 말한다. 예를 들면, 아래의 그림은 $G = ({0, 1, 2, 3, 4, 5}, {{0, 2}, {0, 4}, {0, 5}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5} })$ 를 표현 한 것으로, 정점은 원으로, 간선은 서로 연결하는 선으로 이루어 져있다. 여기서 예를 들면, 0과 1 사이에는 간선이 없으므로, 정점 0과 정점 1은 인접하지 않고, 정점 0과 정점 2는 인접해있다.
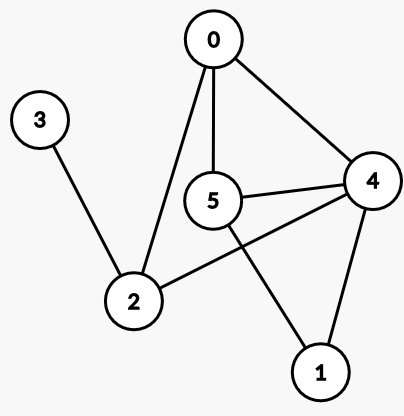
그래프의 색칠
우리는 이 그래프의 정점들을 색칠하려고 한다. 이 정점들을 색칠하는 것은 여러가지 방법이 있을 수 있겠지만, 일반적으로는 정점 $u$와 정점 $v$가 인접하면, 같은 색으로 칠하지 않는것을 그래프의 색칠이라고 한다. 이렇게 가능한 모든 색칠 중에서 색을 가장 적게 쓸 때, 사용한 색의 수를 채색수라고 한다. 수식으로는 함수 $f: V \rightarrow {1, 2, \cdots, k}$ 에 대해서, $u$와 $v$가 인접하면 $f(u) \neq f(v)$ 를 만족하는 함수 $f$가 존재하면, 그래프 $G$는 $k$가지 색으로 색칠이 가능하고, 이런 $k$ 중에 가장 작은 $k$를 채색수라 하고 $\chi(G)$라고 표시한다. 예를 들면, 아래 그림은 위 그래프를 3가지 색으로 칠한 사진이다. 이 그래프는 2가지 이하의 색으로는 칠할 수 없다. (0과 2와 4는 서로 인접하는데, 이들이 서로 다른 색을 가져야 하기 때문이다.) 그래서 이 그래프의 채색수는 3이다.

NP-Completeness
이 그래프의 채색수를 찾는 것은 NP-Complete이라는게 증명되어있다. 일단, $\chi(G)=2$ 인지 판단하는 것은 선형시간 안에 풀리는 문제이다. 우리는 어떤 한 정점의 색을 정하면, 다른 인접한 모든 정점의 색은 유일하게 정해진다. 이를 통해서 DFS등의 탐색을 사용하면 이 그래프가 두가지 색으로 칠해 질 수 있는지, 즉 이분그래프인지 빠른 시간안에 확인할 수 있다. 하지만, $\chi(G)=3$인지 판단하는 문제부터 굉장히 어려운 문제가 되고, NP-Complete문제가 된다.
NP-Completness 증명
일단 우리는 3-SAT문제로 부터 시작할 것이다. 어떤 명제가 참이라는것을 울리는 초록색, 거짓이라는 것을 빨간색, 그리고 임의로 사용되는 색을 노란색으로 표현할 것이다. (이 임의로 사용하는 색은 말 그대로 임의로 사용되는 색이다.)
가젯
우리는 이것을 증명할 때 여러 가젯(Gadget, 기계부품) 을 사용한다. 이 가젯들은, 문제를 푸는데 여러가지 도움을 준다. 우리는 참과 거짓을 그래프의 색으로 잘 옮기려고 한다.
팔레트
일단 우리는, 그래프의 각 정점들을, 참인 빨간색, 거짓인 초록색, 그리고 중간에서 사용되는 색깔인 노란색으로 칠한 것이다. 이렇게 서로 다른 3개의 색을 가지게 만드는 것은 서로 이어주는 완전그래프를 만들면 되고, 다음과 같이 서로 다른 세가지 색이 칠해진다.
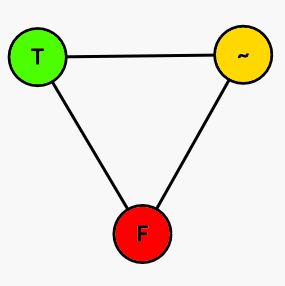
어떤 색을 강제 하는 방법은, 그 색이 아닌 나머지 색들에 그래프를 연결하면 된다.
변수
변수를 표현할 때는 $p$는 참과 거짓, $\neg p$는 $p$와 반대되는 참, 거짓을 가져야 한다. $p$와 $\neg p$를 하나의 정점으로 만든다고 할 때, $p$와 $\neg p$는 임의로 사용되는 색이 되면 안되고, $\neg p$와는 다른 색이어야 한다. 이 조건을 만족하는 색칠법은 두가지 뿐이고, 우리가 원하는 답이 된다.
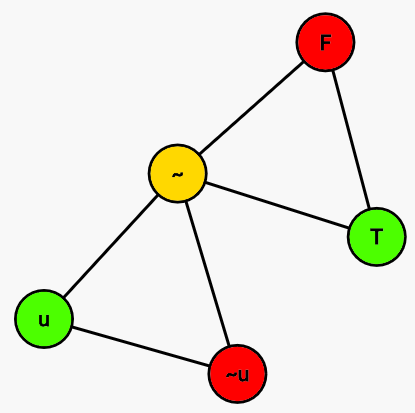
게이트
우리는 $p$ 와 $q$ 가 있을 때 $ p \vee q $ 를 표현하는 방법을 만들어야 한다. 이 OR게이트를 구현을 직접하는 것은 매우 힘든 일이기 때문에 우리는 다음의 가젯을 이용한다.
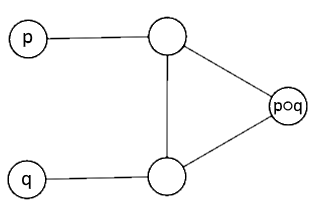
이 가젯 $\circ$ 을 이용하면, $p$와 $q$가 같은 색일때는 $p \circ q$ 가 그 색임을 알 수 있다.
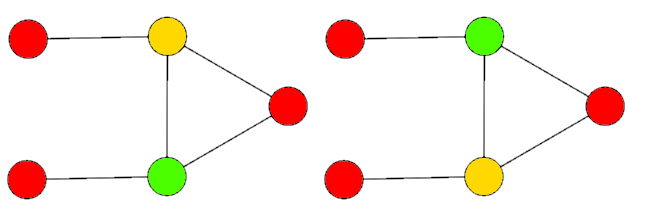
$p$와 $q$가 다른 색일 때는 가능한 모든 색이 될 수 있다.
그렇기 때문에, 우리가 만드려는 $p \circ q$는 두 색이 둘 다 빨간색인 케이스가 아니면 언제든지 초록색으로 칠할 수 있고, or게이트와 비슷한 일을 할 수 있다.
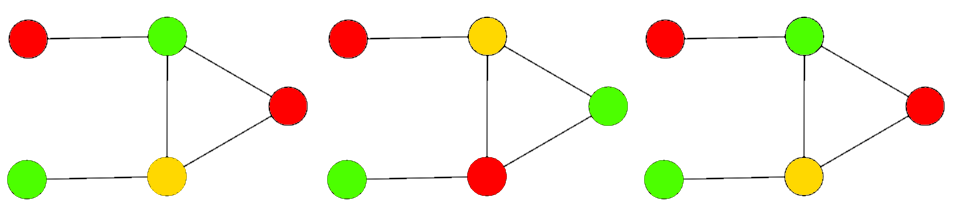
그래서 이 or 게이트를 두개 연속 해서 이을 경우에는, 셋 다 빨간색인 경우에는 빨간색이 강제 되고, 나머지는 초록색을 만들 수 있는 or게이트가 된다.
예제
이렇게 여러 가젯들을 한데 묶으면 다음과 같은 그림이 나오고, 이 그래프를 색칠 해서 $p$ 와 $\neg p$ 에 어떤 색들이 있는지를 알려주는 것이 SAT 문제를 푸는것과 동치이기 때문에, 3가지 색으로 칠할 수 있는지를 판단하는 문제는 NP-Complete 문제이다.
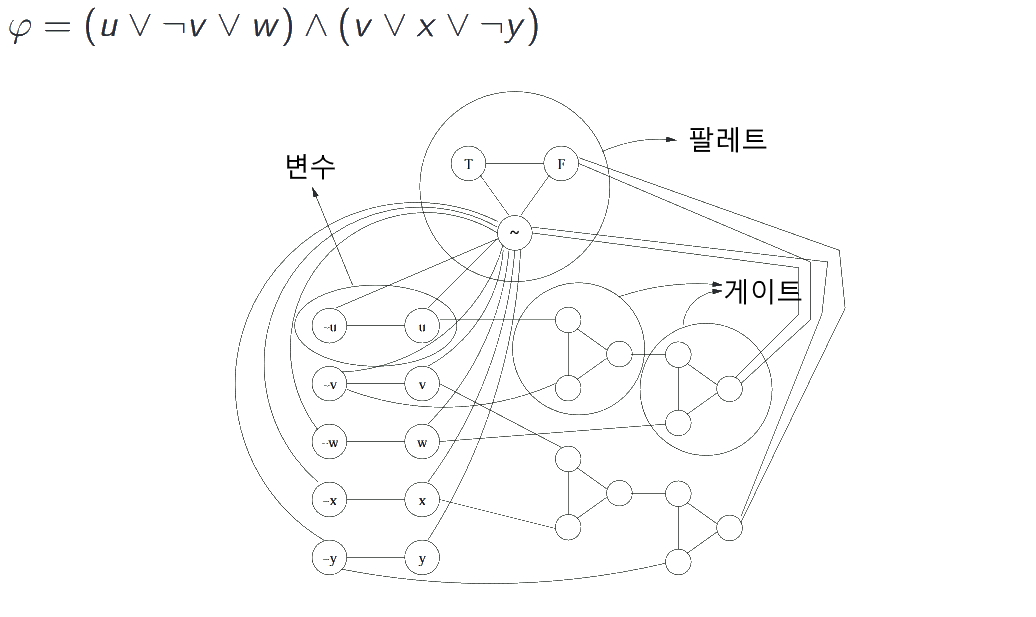
결론
우리는 그래프 색칠 문제가 NP-Complete 인것을 증명했다. 이것은 그래프 색칠 문제가 매우 어려운 문제 중 하나이며, 다항 시간 알고리즘이 없을것이라고 생각되는 문제임을 말한다. 이런 문제를 풀 때는 그래프의 특징들을 잘 활용하여 적절한 근사해나 그래프의 특징을 이용한 다른 해법들을 이용하는게 좋을 것이다.