트리의 종류와 이해
트리의 종류와 이해
0. 목차
- 목차
- tree란?
- tree의 종류
- 결론
- 참고자료
1. tree란?
tree 자료구조는 그래프의 한 종류로, 정의 내리자면
트리란 어떤 노드들의 집합으로 노드들은 각 서로 다른 자식을 가지며 이 때 각 노드는 재사용 되지 않는 구조이다.
tree 에는 여러가지 특징들이 존재한다.
- tree 의 서로 다른 임의의 두 노드에 대해 두 노드를 연결하는 경로는 유일하다.
- tree 에는 사이클을 가지는 노드 집합이 존재하지 않는다.
- tree 반드시 하나의 root가 존재한다. (부모 노드가 존재하지 않는 노드)
이런 특징들을 이용하여 tree의 경우 여러 종류의 문제들을 해결해낼 수 있다.
이제 트리 자료구조에서의 용어에 대해 정의를 해보겠다.
- 노드(node) : 트리는 노드들의 집합으로 트리를 구성하는 것으로 보통 (value) 값과 부모 자식의 정보를 가지고 있다.
- 엣지(edge) : 엣지는 노드들을 연결하는 간선으로 부모 노드와 자식 노드를 연결하게 된다.
- 루트(root node) : 가장 상위 노드로 부모를 가지지 않는다.
- 리프(leaf node) : 가장 하위 노드로 자식을 가지지 않는다.
- 형제 노드 : 같은 부모를 가지는 자식 노드들을 말한다.
- 깊이(depth) : tree에서 부모에서 자식순으로 이동할 때, depth 가 1 증가하며 따라 형제 노드 간의 depth는 일치하며 root node의 depth는 0이된다.
그렇다면 이렇 tree 는 어떠한 방법으로 사용되고 있을까?
눈에 쉽게 보이는 사용으로는 현재 사용하고 있는 PC나 모바일 핸드폰에서의 파일들을 생각해볼 수가 있다.
각 폴더에 대해 자식 폴더 또는 파일들이 있고, 이 때 자식 폴더는 부모가 되어 자식 폴더 또는 파일들을 가지게 된다.
이는 tree로 표현 가능함을 쉽게 알 수 있다.
또한 “tree”의 가장 빈번한 사용이 되는 “Binary Tree” 에서 특정 노드에 대한 접근이
o(N) 이 아닌 o(log N) 이 됨을 이용 하는 것인데, 이는 사용 방도가 무궁무진하므로 후에 구현과 함께 설명한다.
이 외에도 “tree” 에는 여러 가지 방면의 사용이 가능하다. 이를 지금부터 대표적인 자료구조들의 구현과 함께 설명해 보고자 한다.
2. 트리의 종류
그렇다면 “TREE” 자료구조의 종류는 어떤 것이 있을까?
우선 가장 크게 두가지 종류로 나눌 수 있는데, “Binary Tree” 와 “Non-Binary Tree” 이다.
말 그대로 “binary tree” 는 이진 트리로 각 노드에 대해서 두개 이하의 자식을 가짐을 의미하고 “non-binary tree”의 경우 노드의 자식 개수에 대한 제한이 없음을 의미한다.
먼저 “non-binary tree”에 대해 설명해보자.
- non – binary tree
“non – binary tree” 의 가장 대표적인 사용처는 나는 “trie” 자료구조라고 생각한다.
“trie” 자료구조는 문자열 검색의 가장 기본적인 생각에 초안을 둔다.
예를 들어 당신이 운영하는 사이트에서 고객들의 DB를 저장한다고 생각해보자.
그들의 이름을 모두 저장한다고 생각할 때 먼저 생각할 수 있는 구조는 배열이다.
배열의 형태는 DB[int][string] 로 전자는 각 고객의 index 후자는 각 고객의 이름이다.
사람의 수가 n이라 가정하고, 이름의 최대 길이를 m 이라 가정할 때, 공간 복잡도는 O( N * M ) , 하물며 특정 고객에 대한 번호를 찾을 때, 고객의 이름으로 검색할 때, O( N * M ) 이 걸린다.
이는 매우 비효율적인데, 고객의 수가 많아지면 많아질수록 검색은 느려진다.
이를 해결하기 위해 나온 자료구조가 “trie” 이다. 그림과 함께 설명하고자 한다.
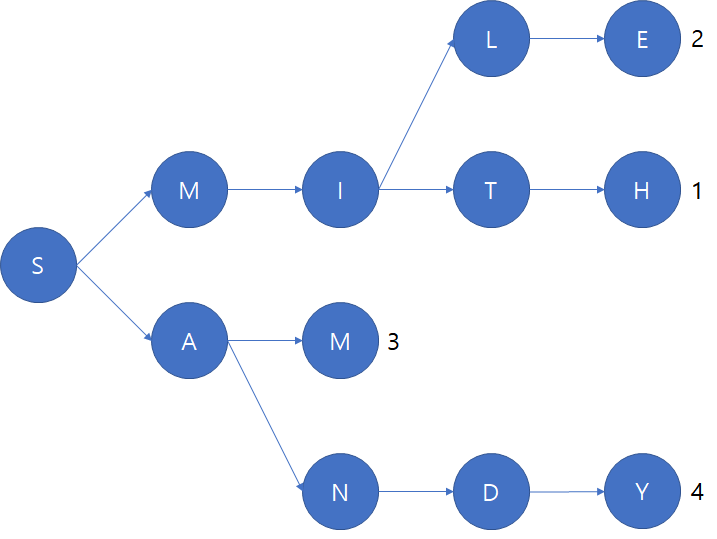
위 그림은 4명의 이름에 대해서 “trie”를 구성한 것이다. 4명의 이름은 {“SMITH”,”SMILE”,”SAM”,”SANDY”} 이다.
각 이름에 대해, 문자열 depth번지의 문자 비교를 통해 일치하는 곳까지 이동 후 새로 주어지는 알파벳으로 가지를 치는 형식이다.
이는 각 노드가 최대 26개의 자식을 가지는 “non -binary tree” 형태로 구성된다.
마지막 leaf 노드에서는 고객의 순번을 정의한 상태이다.
이 때, 검색 시 최대 O( M ) 의 시간 복잡도가 소요된다. 공간 복잡도는 최악의 경우 O( N * M ) 이 된다.
시간 복잡도에서 N이 사라졌음을 확인할 수 있다. 즉 DB에서 고객의 수에 상관없이 그들의 정보를 읽어올 수 있음을 의미한다.
“trie” 에서 보통 단점을 공간 복잡도라고 하는데 26개의 포인터를 매 노드마다 들고 있어야 되기 때문이다.
이는 각 노드 별 자식을 linked list 형태로 표현하면 해결 가능하다.
아래는 문자열이 주어졌을 때 “trie” 를 구성하고 이를 이용해 문자열 해싱을 하는 코드를 직접 구현해보았다.
// TRIE implementation by cjmp1
#include <bits/stdc++.h>
#define FOR(i,a,b) for(int i = a; i <= b; i++)
#define ROF(i,a,b) for(int i = b; i >= a; i--)
using namespace std;
const int MAXN = 50;
char name[MAXN]; int hashcount = 0;
struct node;
struct trie;
struct node { int fhash = -1; char val = (char)0; node *next = NULL; trie *troot = NULL; };
struct trie { node *root = NULL; }*front;
void init();
int hash_F(char* str);
int main() {
ios::sync_with_stdio(false);
int T; cin >> T;
init();
FOR(tcase, 1, T) {
FOR(i, 0, MAXN - 1) name[i] = 0;
cin >> name;
int h_val = hash_F(name);
cout << name << " " << h_val << endl;
}
return 0;
}
void init() {
if(front != nullptr){ delete front; }
front = new trie;
front->root = new node;
}
int hash_F(char* str) {
int num = 0,idx = 0;
node *temp = front->root;
while (str[idx] != 0) {
bool fflag = false;
while (true) {
if (temp->val == str[idx]) { fflag = true; break; }
if (temp->next) { temp = temp->next; continue; }
break;
}
if (fflag) {
if (str[idx + 1] == 0) {
temp->fhash = (temp->fhash == -1) ? ++hashcount : temp->fhash; num = temp->fhash; }
temp = temp->troot->root;
idx++;
}
else {
temp->val = str[idx];
temp->next = new node;
temp->troot = new trie;
temp->troot->root = new node;
if (str[idx + 1] == 0) {
temp->fhash = (temp->fhash == -1) ? ++hashcount : temp->fhash; num = temp->fhash; }
temp = temp->troot->root;
idx++;
}
}
return num;
}
이 외에도 non - binary - tree 는 우리가 사용하는 컴퓨터의 파일시스템을 생각해보더라도, 유용하게 이용됨을 생각 할 수 잇다.
각 루트(부모)디렉토리가 존재하고 그 디렉토리 안에는 파일 또는 자식(child) 디렉토리들이 존재한다. 실제로 메모리주소간의 연결을 통해 이를 구현한다.
- binary - tree
바이너리 트리는 각 노드의 자식이 2개 이하인 형태로 구성되어 있다.
이진트리라고도 하는데 이진트리는 활용도에 따라 여러 알고리즘으로 나뉘어진다. 그 종류를 살펴본다.
- Binary-Search-Tree (BST)
가장 유명하고 접근성이 용이한 알고리즘이다.
각 노드는 left Subtree 와 right Subtree의 루트를 자식으로 가지며 이때 왼쪽 서브트리는 자신보다 작은값을 오른쪽 서브트리는 자신보다 큰 값을 가지는 형태의 이진트리를 일컫는다.
우선 BST의 장점은 자료 입력,삭제,탐색 모두 시간복잡도가 O( log N ) 이라는 점이다.
기본적인 배열 이진탐색의 경우 시간복잡도는 동일하지만 자료의 변경, 삭제가 불가능했다.
또한 linked list 로 구현할 경우 탐색에서 O( N )의 시간이 소요된다. 이를 BST를 이용하여 줄인 것이다. 자세하게 설명해보자.
이진 검색트리의 코드를 함께 보며 분석해보겠다.
// BST implementation by cjmp1
#include <bits/stdc++.h>
#define FOR(i,a,b) for(int i = (a); i <= (b); i++)
using namespace std;
int n,m;
struct Node {
int val;
Node *left = NULL;
Node *right = NULL;
}*root;
void init() {
if (root != NULL) delete root;
root = NULL;
}
void insert(int num) {
Node *tmp = new Node;
tmp->val = num;
if (root == NULL) root = tmp;
else {
Node *temp = root;
while (true) {
if (temp->val == num) return;
if (temp->val < num) {
if (temp->right == NULL) { temp->right = tmp; return; }
temp = temp->right;
}
else if (temp->val > num) {
if (temp->left == NULL) { temp->left = tmp; return; }
temp = temp->left;
}
}
}
}
bool find(int num) {
Node *temp = root;
if (temp == NULL) return false;
while (true) {
if (temp->val == num) return true;
if (temp->val < num) {
if (temp->right == NULL) return false;
temp = temp->right;
}
else if (temp->val > num) {
if (temp->left == NULL) return false;
temp = temp->left;
}
}
}
int main() {
ios::sync_with_stdio(false);
cin >> n;
init();
FOR(i, 1, n) {
int x; cin >> x;
insert(x);
}
cin >> m;
FOR(i, 1, m) {
int x; cin >> x;
cout << find(x) << endl;
}
return 0;
}
코드는 위와 같이 표현 가능한데 기능의 구동이 매우 단순한 것을 볼 수 있다.
Insert() 함수에서는 현재 노드와 새 값을 비교해 새 값이 작다면 left Subtree로 크다면 right Subtree로 계속 이동하여 leaf node를 만날시 삽입을 진행하고 find()함수도 동일하게 진행함을 알 수 있다.
시간복잡도는 왜 log(N)이 되는 것일까? 위 알고리즘의 경우 최대 탐색 횟수는 트리의 depth임을 알 수 있다.
n개의 노드가 주어질 때 이는 매 depth 에서 2개의 노드씩으로 분할되기 때문에, 2^depth = N이 되고 따라서 (time) = depth = log N 이 된다.
물론 여기서 알고리즘의 가장 큰 약점을 확인할 수 있다. 위 알고리즘을 이용해 정렬을 하면 논리적으로 O(N log N) 시간이 소요되어야 한다.
그러나 dataset을 증가수열의 형태라고 가정해보자.
그러면 tree는 계속 오른쪽 subtree에 노드를 생성할 것이고 이는 dataset의 크기가 n이라 가정할 때, depth n에 각 depth 당 하나의 노드를 가지는 트리를 형성하게 된다.
이는 탐색에 걸리는 시간이 O(N) 이되고 즉 정렬에 필요한 시간도 O(N^2) 이 된다.
그렇다면 BST 알고리즘은 O(log N) 이 아닌것일까?
조금만 생각해보면 log N에 가능함을 알 수 있다. N의 depth를 가지는 tree의 중간 depth 위치에 있는 지점을 root 로 잡아보자.
그러면 처음 사진 에서 두번째 사진이 된다. 또 이 작업을 동일하게 한 번더 시행하면 3번째 사진 형태가 된다.
마지막사진 형태로 변형하게 되면 시간복잡도가 O(log N)으로 돌아옴을 알 수 있다. 즉 노드를 삽입할 때 뭔가 다른 방법이 필요함을 알 수 있다.
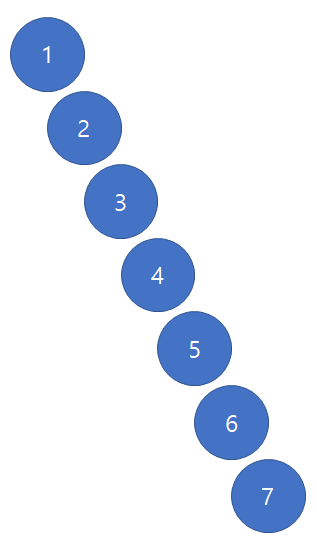
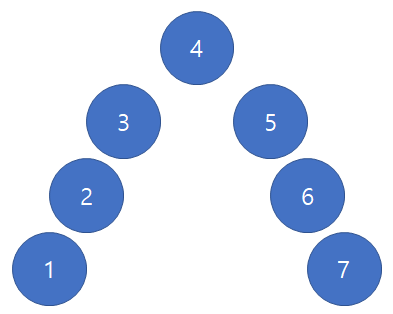
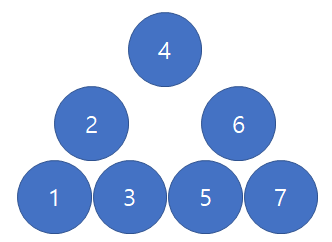
이 아이디어를 접목시킨 것이 “Balanced binary search tree” 이다. 즉 “BST”를 구현함에 있어서 좌 우 subtree를 균형을 잡아주며 노드를 삽입하자는 것이다. 이 알고리즘의 예로는 여러가지가 있다.
그 예로 “Splay tree”, “AVL tree”, “Red Black tree” 가 대표적인 예시이다. 이 알고리즘은 모두 self balancing 을 추구하지만 사용되는 경우가 매우 다르다.
우선 Splay tree는 최근에 방문한 노드를 상단으로 위치함으로서, 자주 방문하는 노드의 수가 적을경우에 적합하다. Splay tree는 노드 배치를 위에서 말했듯이 사용자에 최적화되어 있으므로 실제 O(log N) 보다 빠르게 실행된다.
반면 AVL tree와 Red Black tree는 호출되는 API의 빈도수에 따라 알고리즘의 성능이 달라진다.
| AVL tree는 Search»(Insert | Delete) 일때 더 효율적이고 Red Black Tree는 그 반대이다. |
이는 AVL tree가 tree를 재구성 하는 과정(삽입/삭제)에서 회전의 수가 많아지기 때문이다.
이중 직접 구현해 본 것은 Red Black Tree 와 Splay Tree 인데 STL구현시 사용된 RBT를 집중적으로 설명해보겠다. 소스코드를 보기전에 RBT(red black tree) 가 어떻게 작동하는지를 보고자 한다. RBT는 다음과 같은 조건을 만족하게 tree를 구성한다.
-
각 노드는 RED or BLACK 색상을 갖는다.
-
트리의 루트는 항상 BLACK 색상이다.
-
반드시 두 인접한 노드는 둘다 RED색상이 아니어야 한다.
-
특정 노드에서 아래에있는 (depth가 더 큰) 모든 NULL node 까지의 path에서 만나는 BLACK 색상의 노드의 수가 동일하다.
이 4번째 조건만 보더라도 우선 균형된 tree를 만들 수 있을 것 같다는 생각을 할 수 있지만 좀 더 자세히 증명해보겠다.
정리 : RBT 가 n개의 노드를 가질 때, 그 최대 height(depth) 는 2*log(n+1) 이다.
증명 : 어떤 노드 x를 루트로 하는 RBT의 서브트리가 2^{(bh(x))-1} 개의 노드를 가진다고 가정하자. bh(x)는 x에서 BLACK 색상 노드의 높이다. (null 까지의 개수)이를 블랙색상높이라 하자.
이때, bh(x)=0 → x is a leaf → 2^0-1=0 임은 정의에 의해 자명하다.
따라서 귀납법을 이용해보자. . bh(x) 보다 낮은 BLACK 색상 높이에 대해서 위 정리가 참이라고 가정하면
-
x 가 BLACK 일 때, 각 subtree 의 BLACK 높이는 . bh(x)-1 이 된다.
-
X 가 RED 일 때, 각 subtree 의 BLACK 높이는 . bh(x) 가 된다.
따라서 subtree 의 내부 노드의 수는 다음을 만족하게 된다.
n ≥ 2^{(bh(x)-1)} - 1 + 2^{(bh(x)-1)} - 1 + 1 ≥ 2^{bh(x) -1}
이제 h를 RBT의 높이라고 하자, 루트에서 leaf node 까지 RED 가 연속이 불가능하므로 최소 BLACK 노드는 h/2 이상임을 알 수 있다. 이를 표현하면
bh(x) ≥ h/2, and n ≥ 2^{(h/2)-1} , so n + 1 ≥ 2^{(h/2)}
양쪽에 log를 취하면
log(n+1) ≥ h/2, so h ≤ 2log(n+1)
이 결론으로 도출된다. 따라서 RBT의 높이는 항상 유지됨을 알 수 있다.
그럼 이제 RBT 의 삽입과 삭제는 어떤 방식으로 이루어지는지 살펴보도록 하자.
Insertion
-
삽입할 위치를 BST와 동일한 방식으로 검색해 찾는다.
-
그 위치에 노드를 추가하고 RED색상을 입힌다.
-
만약 부모 색상이 BLACK 이면 종료, RED면 4번을 진행한다.
-
삼촌노드의 색깔을 확인한다. (삼촌 노드란 부모의 형제노드를 말한다.) 만약 삼촌 노드의 색깔이 RED라면 RECOLORING() 을 BLACK 이라면 RESTRUCTING()을 실행한다.
-
RECOLORING()의 경우 부모와 삼촌 을 BLACK으로 바꾸고 부모의 부모노드를 RED로 바꾼다. 이 때 유의할점은 부모의 부모노드를 RED로 바꾸는 과정에서 또 다시 RED 연속이 생길 수 있다. 따라서 이는 반복될 수 있고 root노드까지 확인한후 root 는 항상 BLACK을 마지막에 칠하게 된다.
-
RESTRUCTING()의 경우 자신 부모 그리고 부모의 부모 3 노드를 오름차순 정렬 후 중간 노드가 3노드중에서 root노드를 취하고 가장 작은값이 왼쪽 subtree의 root 큰값이 오른쪽 subtree의 root가 되도록 변경하는 과정이다.
-
### Deletion
-
삭제할 위치를 BST와 동일한 방식으로 검색해서 찾는다.
-
그 위치의 노드 색상이 RED 라면 균형에 문제를 주지 않으므로 삭제하고 종료한다.
-
색상이 BLACK 이라면 그 노드가 삭제되고 대체될 노드를 확인한다. (자식 노드중 큰 값) 그 노드의 색상이 RED라면 BLACK으로 변환하고 노드를 대체한후 종료. BLACK일 경우 다음으로 이동
-
BLACK 이라면 그 노드는 이중 블랙 노드가 된다. 따라서 이 때는 이중 블랙 노드의 형제노드의 색상을 확인한다. RED 라면 BLACK이 되게 바꾸어 줘야하는데 이는 형제를 BLACK 부모를 RED로 칠한 후 부모기준 leftrotate를 실행하면 된다. 그렇게 형제노드의 색상이 BLACK이라면 다음으로 이동
-
5번에건 세가지 경우로 나누어서 처리한다.
-
형제의 양쪽자식이 BLACK인 경우 : 형제노드를 RED로 바꾸고 이중 블랙 노드를 부모에 전달한다(root 에 도달하면 종료).
-
형제의 자식이 BLACK, RED 인 경우 : 형제노드를 RED로 바꾸고 left 를 BLACK으로 바꾼 후에 형제노드 기준 rightrotate를 실행한다.
-
형제의 양쪽자식이 RED인 경우 : 부모노드의 색을 형제노드에게 넘기고 right들을 BLACK으로 바꾼 후에 부모노드 기준 leftrotate를 실행한다. 이를 정확히 그대로 코드로 표현하면 아래와 같다.
-
// RedBlackTree by cjmp1
// 1. Every node has a clor either red or black
// 2. Root of tree is aways black
// 3. There are no twoadjacent red nodes(A red node cannot have a red parent or child).
// 4. Every path froma node (including root) to any of its descendant NULL node has the same number of black nodes.
// complexity{
// Insert : ( log n )
// Search :o( log n )
// }
// earch >> (Insert,Delete) --> RBT >> AVL
//Search << (Insert,Delete) --> RBT << AVL
#nclude <bits/stdc++.h>
define FOR(i,a,b) for(int i = (a); i <= (b); i++)
using namespace std;
const int maxN = 1000011;
typedef enum {
RED,
BLACK,
DBLACK
}COLOR;
typedef enum {
INSERT,
DELETE,
FIND
}CMD;
struct Node {
int v;
COLOR c = RED;
Node *left = NULL;
Node *right = NULL;
Node *parent = NULL;
}*root,*temp;
void RBT_init(), RBT_insert(), fix_insertion(Node *&ptr), fix_deletion(Node *&ptr), RBT_delete(),
leftRotate(Node *& ptr), rightRotate(Node *& ptr), show_Tree(), dfs(Node *&node);
Node *insertion(Node *&root, Node *&ptr), *deletion(Node *&root, int data), *minValueNode(Node *&node);
bool RBT_search();
int max_size = 0, nsize = 0;
struct showT {
int v;
COLOR c;
}RBTree[maxN];
ifstream in("input.txt");
ofstream out("output.txt");
int main() {
in.is_open(); out.is_open();
ios::sync_with_stdio(false);
int T; in >> T;
RBT_init();
while (T--) {
int cmd; in >> cmd;
switch (cmd) {
case INSERT: RBT_insert(); break;
case DELETE: RBT_delete(); break;
case FIND: out << (RBT_search() ? "Found" : "Not Found") << endl; break;
default: break;
}
show_Tree();
}
in.close(); out.close();
return 0;
}
void dfs(Node *&node) {
RBTree[nsize].v = node->v; RBTree[nsize].c = node->c;
max_size = max_size < nsize ? nsize : max_size;
if (node->left != NULL) { nsize = nsize << 1; dfs(node->left); nsize = nsize >> 1; }
if (node->right != NULL) { nsize = (nsize << 1) + 1; dfs(node->right); nsize = nsize >> 1; }
}
void show_Tree() {
nsize = 1; max_size = nsize;
dfs(root);
FOR(i, 1, max_size) {
out << RBTree[i].v << " " << RBTree[i].c << "| ";
}
out << endl;
}
void RBT_init() { if (root != NULL) { delete root; } root = NULL; }
Node *insertion(Node *&root, Node *&ptr) {
if (root == NULL) { return ptr; }
if (ptr->v < root->v) {
root->left = insertion(root->left, ptr);
root->left->parent = root;
}
else if (ptr->v > root->v) {
root->right = insertion(root->right, ptr);
root->right->parent = root;
}
return root;
}
COLOR getColor(Node *&ptr) {
if (ptr == NULL) return BLACK;
return ptr->c;
}
void setColor(Node *&node, COLOR cl) {
if (node == NULL) return;
node->c = cl;
}
void RBT_insert() {
Node *node = new Node();
in >> node->v; setColor(node, RED);
root = insertion(root, node);
fix_insertion(node);
}
void fix_insertion(Node *&ptr) {
Node *parent = NULL;
Node *grandparent = NULL;
while (ptr != root && getColor(ptr) == RED && getColor(ptr->parent) == RED) {
parent = ptr->parent;
grandparent = parent->parent;
if (parent == grandparent->left) {
Node *uncle = grandparent->right;
if (getColor(uncle) == RED) {
setColor(uncle, BLACK); setColor(parent, BLACK); setColor(grandparent, RED);
ptr = grandparent;
}
else {
if (ptr == parent->right) {
leftRotate(parent);
ptr = parent;
parent = ptr->parent;
}
rightRotate(grandparent);
swap(parent->c, grandparent->c);
ptr = parent;
}
}
else {
Node *uncle = grandparent->left;
if (getColor(uncle) == RED) {
setColor(uncle, BLACK); setColor(parent, BLACK); setColor(grandparent, RED);
ptr = grandparent;
}
else {
if(ptr == parent->left){
rightRotate(parent);
ptr = parent;
parent = ptr->parent;
}
leftRotate(grandparent);
swap(parent->c, grandparent->c);
ptr = parent;
}
}
}
setColor(root, BLACK);
}
void leftRotate(Node *&ptr) {
Node *rightSubT = ptr->right;
ptr->right = rightSubT->left;
if (ptr->right != NULL) ptr->right->parent = ptr;
rightSubT->parent = ptr->parent;
if (ptr->parent == NULL) root = rightSubT;
else if (ptr == ptr->parent->left) ptr->parent->left = rightSubT;
else ptr->parent->right = rightSubT;
rightSubT->left = ptr;
ptr->parent = rightSubT;
}
void rightRotate(Node *&ptr) {
Node *leftSubT = ptr->left;
ptr->left = leftSubT->right;
if (ptr->left != NULL) ptr->left->parent = ptr;
leftSubT->parent = ptr->parent;
if (ptr->parent == NULL) root = leftSubT;
else if (ptr == ptr->parent->left) ptr->parent->left = leftSubT;
else ptr->parent->right = leftSubT;
leftSubT->right = ptr;
ptr->parent = leftSubT;
}
bool RBT_search() {
int val; in >> val;
Node *temp = root;
while (true) {
if (temp == NULL) break;
if (temp->v == val) return true;
if (temp->v < val) temp = temp->right;
else temp = temp->left;
}
return false;
}
Node *minValueNode(Node *&node) {
Node *ptr = node;
while (ptr->left != NULL) ptr = ptr->left;
return ptr;
}
Node *deletion(Node *&root, int data) {
if (root == NULL) { return root; }
if (root->v < data) return deletion(root->right, data);
if (root->v > data) return deletion(root->left, data);
if (root->left == NULL || root->right == NULL) return root;
Node *temp = minValueNode(root->right);
root->v = temp->v;
return deletion(root->right, temp->v);
}
void fix_deletion(Node *&node) {
if (node == NULL) return;
if (node == root) { root = NULL; return; }
if (getColor(node) == RED || getColor(node->left) == RED || getColor(node->right) == RED) {
Node *child = node->left != NULL ? node->left : node->right;
if (node == node->parent->left) {
node->parent->left = child;
if (child != NULL) child->parent = node->parent;
setColor(child, BLACK);
delete (node);
}
else {
node->parent->right = child;
if (child != NULL) child->parent = node->parent;
setColor(child, BLACK);
delete (node);
}
}
else {
Node *sibling = nullptr;
Node *parent = nullptr;
Node *ptr = node;
setColor(ptr, DBLACK);
while (ptr != root && getColor(ptr) == DBLACK) {
parent = ptr->parent;
if (ptr == parent->left) {
sibling = parent->right;
if (getColor(sibling) == RED) {
setColor(sibling, BLACK); setColor(parent, RED);
leftRotate(parent);
}
else {
if (getColor(sibling->left) == BLACK && getColor(sibling->right) == BLACK) {
setColor(sibling, RED);
if (getColor(parent) == RED) setColor(parent, BLACK);
else setColor(parent, DBLACK);
ptr = parent;
}
else {
if (getColor(sibling->right) == BLACK) {
setColor(sibling->left, BLACK); setColor(sibling, RED);
rightRotate(sibling);
sibling = parent->right;
}
setColor(sibling, parent->c);
setColor(parent, BLACK); setColor(sibling->right, BLACK);
leftRotate(parent);
break;
}
}
}
else {
sibling = parent->left;
if (getColor(sibling) == RED) {
setColor(sibling, BLACK); setColor(parent, RED);
rightRotate(parent);
}
else {
if (getColor(sibling->left) == BLACK && getColor(sibling->right) == BLACK) {
setColor(sibling, RED);
if (getColor(parent) == RED) setColor(parent, BLACK);
else setColor(parent, DBLACK);
ptr = parent;
}
else {
if (getColor(sibling->left) == BLACK) {
setColor(sibling->right, BLACK); setColor(sibling, RED);
leftRotate(sibling);
sibling = parent->left;
}
setColor(sibling, parent->c);
setColor(parent, BLACK); setColor(sibling->left, BLACK);
rightRotate(parent);
break;
}
}
}
}
if (node == node->parent->left) node->parent->left = NULL;
else node->parent->right = NULL;
delete(node);
setColor(root, BLACK);
}
}
void RBT_delete() {
int val; in >> val;
Node *node = deletion(root, val);
fix_deletion(node);
}
RBT 는 C++ 에서 제공하는 STL(Standard library) 에 속하는 자료구조(map, set) 등 여러가지를 구현할 때 이용된 알고리즘이다. 따라서 알아두면 매우 유용하고 구현해 보는 과정에서 tree 구조에 대한 이해를 더욱 견고히 할 수 있어서 구현해 보는 것을 추천한다.
- Segment tree
BST의 다른 종류인 Segnent tree를 살펴보자. Segment tree는 이름에서도 볼 수 있듯이 ree를 이용해 구획을 나누는 방법이다.
어떤 정수로 이루어진 배열 A를 생각해보자.
우리는 배열 A에서 연속된 구간의 합을 구하고자 한다. 즉 sum{i = a~b} (a <= b , a,b in Z) 값을 구하고자 한다.
이 문제의 경우 S[i] = sum{i = 1~n} A[i] (n = length(A), S[0] = 0) 를 구함으로서 A[a to b] = S[b] - S[a-1] 을 이용해 O(1)에 구할 수 있다.
그렇지만 만약 1 <= j <= n , (j in Z) 인 j에 대해 A[j] 값이 변경된다고 가정해보자.
그러면 우리는 위의 값을 구하기 위해서는 S[i] 값들을 모두 갱신해야됨을 알 수 있다. 이는 O(N)의 시간이 소요되는데
변경의 쿼리개수가 q일 경우 O(nq)가 되고 이는 매우 비효율적이다.
이를 해결할 수 있는 것이 Segment tree이다. Segment tree의 각 노드들은 다음과 같은 정의를 갖는다.
- 각 노드의 값 = 왼쪽 자식의 값 + 오른쪽 자식의 값
이렇게 두고 leaf node에 각 배열의 실제 값을 저장해준다. 그렇게 되면 root node 에는 A의 모든 원소합이 구해진다.
Segment tree의 구현을 함께 보자.
// Segment tree by cjmp1
#include <bits/stdc++.h>
#define FOR(i,a,b) for(int i = (a); i <= (b); i++)
#define MAXN 100010
using namespace std;
typedef enum {
CHANGE,
SUM
}CMD;
int T[MAXN];
int A[MAXN], ans, cnt = 0,n,x,xx;
void init(), change(), sum();
int main() {
ios::sync_with_stdio(false);
cin >> n;
x = 1;
while (true) {
x = x << 1;
if (x >= n) break;
}
FOR(i, 1, n) { cin >> A[i]; }
init();
int q; cin >> q; // query
FOR(tc, 1, q) {
int cIdx; cin >> cIdx;
ans = 0;
switch (cIdx) {
case CHANGE: change(); cout << "#" << tc << " " << "Changed" << endl; break;
case SUM: sum(); cout << "#" << tc << " " << ans << endl; break;
default: cout << "#" << tc << " " << "CMD_ERROR" << endl; break;
}
}
return 0;
}
void init() {
FOR(i, 1, n) {
T[x + i - 1] = A[i];
xx = (x + i - 1) >> 1;
while (xx > 0) {
T[xx] = T[xx] + A[i];
xx = xx >> 1;
}
}
}
void change() {
int p,q; cin >> p >> q;
int tmp = T[x + p - 1];
xx = x + p - 1;
while (xx > 0) {
T[xx] = T[xx] - tmp + q;
xx = xx >> 1;
}
}
void sum() {
int l, r; cin >> l >> r;
l = x + l - 1; r = x + r - 1;
while (true) {
if (l % 2 == 1) { ans = ans + T[l++]; }
if (r % 2 == 0) { ans = ans + T[r--]; }
if (l > r) {
if (l == r) ans = ans + T[l];
break;
}
l = l >> 1; r = r >> 1;
}
}
코드에서 확인할 수 있듯이, x 즉 log_{2}x가 높이가 되는 트리를 구성할 수 있다. 이 때, 삽입 및 변경, 그리고 구간합을 구하는데에 있어서 모두 o(logN) 이 소요됨을 알 수 있다.
그런데 만약 query가 단순히 숫자 하나를 바꾸는 것이 아닌 구간으로 주어진다고 생각해보자.
즉 “a~b 까지 의 값을 5씩 더하라” 라고 query가 주어지면 이를 해결하기 위해서는 O(qNlogN) 이 소요될 것이다. N을 제거해주기 위해선 우리는 Segment tree의 근본적인 개념을 다시 한 번 확인해줄 필요가 있다. Segment tree는 각 노드가 일정한 구간의 정보를 포함하고 있다.
그렇다면 구간에 대한 정보 변경도 그 구간을 대표하는 노드만 바꾸어 주면 된다고 생각 할 수 있다. 그림으로 표현해보자.
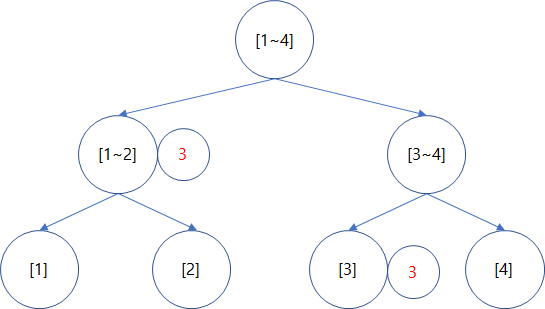
[1 ~ 4] 길이를 가지는 배열 A에서 구간 [1 ~ 3] 값을 모두 3씩 더한다고 생각해보자.
우리는 위 그림과 같이 구간 [1 ~ 3]을 대표하는 노드만 수정을 해준다.
하지만 이렇게 하면 구간 [1] 과 구간 [2] 에는 제대로 정보가 전해지지 않는다. 이를 위해 후에 실제 합을 구하는 과정에 있어서 그 구간을 지나칠 때에 변화를 전파하면서 구현해 줄 수 있다.
이러한 알고리즘을 필요할 때만 게으르게 전파한다고 해서 Lazy Propogation 이라고 한다.
- Others
우리는 지금까지 본 트리를 말미암아 볼 때 1차원 배열에 대한 정보를 표현할 때 트리가 사용됨을 확인할 수 있다.
그렇다면 2차원상의 정보를 접근할 때 있어서 트리는 큰 효과를 보여주지 못하는 것일까? 라는 의문을 가질 수 있디.
결론은 그렇지 않다. 이를 보여주기 위해 K-D tree 를 소개하고자 한다.
K-D tree는 K차원을 트리로 구조화하는 자료구조라고 생각 할 수 있다.
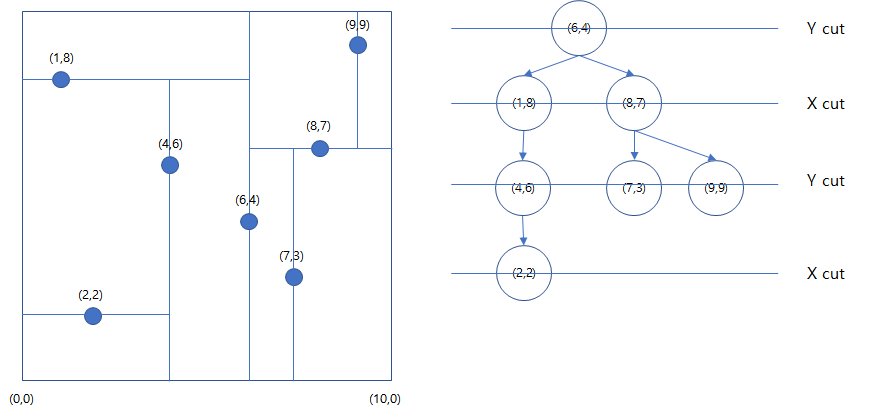
위의 그림은 2차원상의 점들을 K-D tree로 표현한것을 보여주고 있다. 이렇게 2차원 또는 K차원의 좌표또는 정보를 tree로 표현함으로서, 우리는 공간적/시간적으로 많은 효과를 볼 수 있다. 실제로 K-D tree를 이용하면,
NN알고리즘 (주어진 점에서 가장 가까운 점 찾기) 구현이 가능하고, 이를 balance 됬다는 가정하에 O(logN)에 구할 수 있다.
3. 결론
- 이렇게 우리는 여러가지 종류의 tree가 존재함을 알 수 있었다. 실제로 tree 자료구조의 발견이 개발자들에게 큰 도움을 준것은 자명하다.
또한 BST및 그 개념은 N개의 원소에 대해 여러 방향으로 더 빠르고 유용한 방법임을 확인할 수 있었다.
여기서 하나의 궁금증을 가질 수 있다. BST는 log_{2}n을 만들어냈다.
그렇다면 각 노드의 자식을 3개로 만든다면 log_{3}n을 만들어 낼수 있지 않을까?
이렇게 된다면 더 많은 자식을 가질 수록 성능이 향상된다고 생각할 수 있다.
하지만 3개의 자식으로 분할하는 것은 실제로 그렇게 좋은 성능을 내지 못한다.
n개의 노드에 대해서 3잔트리와 2진트리의 성능을 비교해보자. 각 노드별로 log의 시간이 소요되므로,
nlog_{3}n , nlog_{2}n 이라고 할 수 있다. 그렇다면 3진트리가 더 빠른 것일까? 결론은 “아니다” 이다.
실제트리의 구현에 있어서 이진트리를 구성할 때는 한노드에 대해서 1개의 조건문이 필요했다.(작거나 크거나)
삼진트리를 구성할 때는 한 노드에 대해서 분기를 결정할 때, 최소 2개의 조건문이 필요하다.
따라서 실제 걸리는 상수를 포함한 시간복잡도는 2nlog_{3}n, nlog_{2}n 이라고 볼 수 있다.
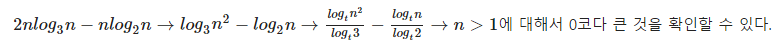
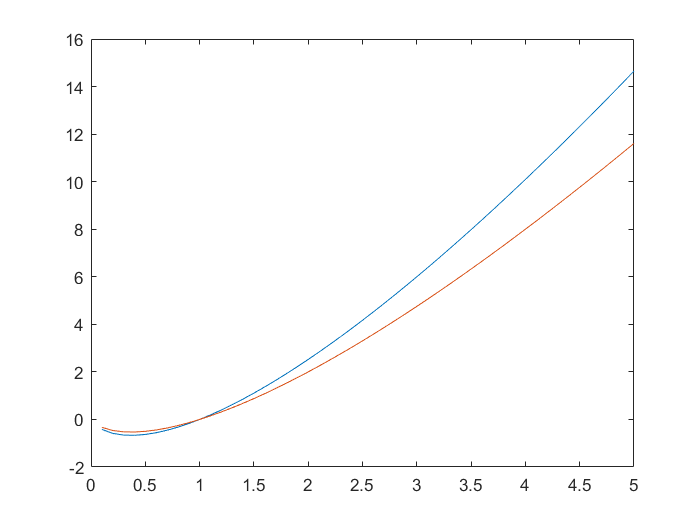
따라서 분기를 1개의 조건문으로 할 수 있지 않는 한 이진트리가 최적이 됨을 확인할 수 있다.
유용한 트리는 알고리즘 공부에 있어서 반드시 짚고 넘어가야하는 중요한 자료구조이다. 트리에 대한 이해는 전반적인 자료구조에 대한 이해에 있어서 큰 도움을 주는 것 같아 큰 의미를 가진다. 이 글을 읽고 트리에 대한 이해를 다졌으면 좋겠다.
4.참고자료
https://www.geeksforgeeks.org/red-black-tree-set-1-introduction-2/
https://www.geeksforgeeks.org/red-black-tree-set-2-insert/
https://www.geeksforgeeks.org/red-black-tree-set-3-delete-2/