목차
개요
이 포스트를 쓰며
두달 전에 Manacher’s Algorithm 에 대해 소개했다. 이번에는 그것의 연장선상이며, 조금 지엽적이면서도 활용도가 높은 Palindromic Tree에 대해서 소개하고자 이 포스트를 쓰게 되었다. 이 포스트를 이해 하기 위해서는 간단한 오토마타에 대한 지식을 요구한다. 또한 KMP Algorithm에 대해 알고 있으면 이해하기 훨씬 수월하다. 또한 Manacher’s Algorithm 에 대한 지식이 없다면 Manacher’s Algorithm 에 대한 포스트를 한번 읽어보길 바란다. 또한 Trie에 대한 지식이 있으면 역시 도움이 된다.
간단한 원리
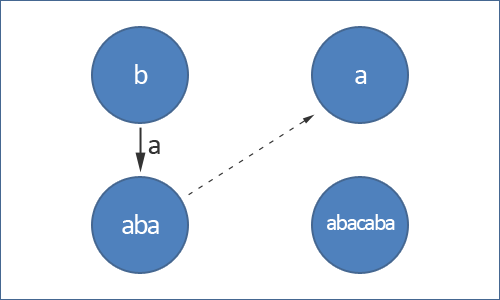
우선 Suffix Link의 개념에 대해 간단히 소개하겠다. Suffix Link란, Palindromic Tree를 구축하는 데 있어서 가장 중요한, 일종의 KMP의 Fail Function과 같으며, 현재 노드에 해당하는 Palindrome의 Suffix중, 가장 긴 것으로 돌아가는 링크를 의미한다. 이는 KMP의 Fail Function이 Prefix 와 Suffix가 가장 길게 일치하는 것을 구하는 것과 비슷하다고 생각하면 편하다. 그러면 KMP를 구축하듯이, Tree를 만들되, 이 Suffix Link로 현재 노드에서 다음노드로 전진할 수 없는 상황에서 돌아가게 하는 것이다. 그리고 이러한 Suffix Link는 구축과 탐색 둘 다 용이하게 사용된다. 일단, 홀수 Palindrome과 짝수 Palindrome을 동시에 다룰 수 있도록 기본적으로 두개의 Root를 가지고 있게 된다. 이제 본격적으로 설명을 시작하겠다.
개념
중요한 성질
우선 중요한 성질부터 살펴보자
어떤 String $s$ 에 대해, Substring $s’$ 중 서로다른 Palindrome의 개수는 $s$의 길이를 n이라고 할때, 많아봐야 n개 이다.
증명은 간단하다. 우선 중요한 정의부터 내리겠다. $x \in \Sigma$, $y \in \Sigma \cup {\epsilon}$, ${a, b, c} \subset Strings$, $s^{R}$ 은 string $s$를 뒤집은 것 을 의미한다.
여기서 시그마는 문자의 집합, 즉, $x$는 문자 하나를 의미한다. $y$는 $\epsilon$즉, 빈 문자를 포함한 문자를 의미한다. 이때, $x$는 새롭게 출현하는 문자, $y$는 그 어떤 palindrome의 중심이 되는 문자라고 해보자. $a$, $b$, $c$ 들은 각각 어떤 문자열을 의미한다. 물론 빈 문자열도 가능하다.
어떤 문자열 $s$의 뒤에 $x$를 붙였을 때 발생하는 팰린드롬 중, 제일 긴 팰린드롬은 $xaya^{R}x$ 로 나타낼 수 있다.
자, 여기서 한가지 알아낼 수 있는 사실은 만약 여기서 이 팰린드롬 보다 길이가 작은 팰린드롬이 존재한다고 가정 해보자. 이때 이 팰린드롬은 반드시 $s$에 속할 수 밖에 없다. 그것에 대한 증명은 간단하다.
우선 $a^{R}$에 속하는 경우 $xaycxbx$ 꼴로 나타낼 수 있다. 이때, $cxb = a^{R}$ 과 같으며, 이때 $a = b^{R}xc^{R}$로 나타낼 수 있다.
여기서
이때 $xbx$ 가 팰린드롬이면 $b$역시 팰린드롬이다. 따라서 $b = b^{R}$이다. 즉, $a = bxc^{R}$ 이며, $xbxc^{R}ycxbx$ 로 나타낼 수 있으며, 이는 $xbx$가 $s$안에 속한다는걸 보인다.
이렇게 유도 할 수 있다. 이때 이때 $x$가 $a^{R}$ 이 아닌 $a$에 속하는 경우를 생각해보자.
$xbxcya^{R}x$ 로 나타낼 수 있게 되는데, 이 경우에, $xcya^{R}x$가 팰린드롬이 되게 된다. 이때, $a=bxc$ 이므로 $a^{R}=c^{R}xb^{R}$ 이 된다. 이때, $xcya^{R}x = xayc^{R}x$ 이므로, $xcya^{R}x = xcyc^{R}xb^{R}x = xbxcyc^{R}x$ 가 되며, 이때, 처음 식에 대입하게 되면, 다음의 식을 얻게 된다.
$xbxcyc^{R}xb^{R}x$
여기서 $xbxcyc^{R}x$ 가 $xcya^{R}x$ 와 같으므로, 즉, $s$안에 속하게 된다. 이를 통해 얻어낼 수 있는 결론은 다음과 같다.
$s$의 뒤에 임의의 문자 $x$를 추가해서 새로운 문자열을 만들 때, 늘어날 수 있는 palindrome인 substring은 많아야 1개이다. 즉, 빈 문자열로 부터 점점 문자를 붙여나가서 어떤 문자열을 만들때, Palindrome인 substring은 n보다 작거나 같을 수 밖에 없다.
이 아이디어는 추후 Palindromic Tree를 구축할 떄 쓰이게 된다.
Palindromic Tree 구축
먼저, 1번과 2번 노드를 루트로 설정한다. 그리고 2번 노드에 Suffix Link로 1번노드를 연결하고 1번노드는 더 이상 후퇴할 수 없는 상황, 즉, 길이가 1인 팰린드롬에 연결시켜주는 마지막 보루이므로 Suffix Link는 존재할 수 없다. 그리고 각 노드들이 나타내고 있는 팰린드롬의 길이를 저장할 필요가 있다. 이때, 1번노드는 길이가 -1 이며, 2번 노드는 길이가 0이다. 이는 길이가 1인 팰린드롬과 길이가 2인 팰린드롬 두가지를 모두 갖기 위함이다. 이후 연결 과정은 Trie와 매우 유사하다. 먼저 마지막에 만들었던 Palindrome의 위치에 대해서 x를 추가했을때 Palindrome을 만들 수 있다면 그 위치에서 바로 x를 추가하기만 하면 된다. 하지만, 그렇게 하지 못한다면은 Suffix Link를 타고 다음 만들 Palindrome 을 찾아내는 것이다.
아래의 그림을 보자
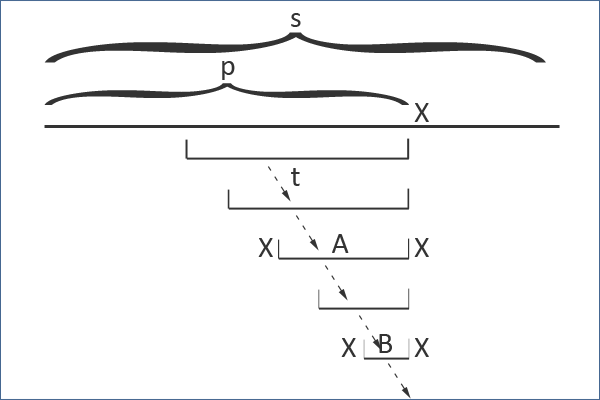
이 그림에서 전체 String을 S라고 했을때 내가 지금 P까지 진행된 상황인 것이다. 이때 그 다음 P+1을 볼때 X가 추가 되었는데, XAX의 팰린드롬이 존재하게 되는 경우를 찾기 위해 Suffix Link를 계속 타고 내려가게 되는것이다. 그렇게 새롭게 만들어진 노드에 대해서 새로 다시 연결하려면 타고 내려가던 Suffix Link를 그대로 다시 타고 내려가서 XAX의 Suffix Link를 XBX로 하는것이다. 만약 빈문자열 까지 내려가게 된다면, 즉 1번 노드 까지 내려가게 된다면 X 자기 자신을 Suffix Link로 사용하게 되는것이다. 자 그렇다면 이때, Suffix Link인 XBX가 없을 수 가 있을까? 답은 아니다 이다. 항상 만들어져 있다. 그 이유는 위 증명을 생각해보면 간단하다. XBX는 반드시 P 어딘가에서 적어도 한번 출현했을 것이기 때문이다.
그리고 이 과정에서 주의할 점이 있다. 만약 X를 추가했을때, X에서 아무것도 만들지 못할 경우엔 자동으로 X 자기자신을 팰린드롬으로 하는 길이가 1인 팰린드롬이 만들어지게 되는데, 이 경우 Suffix Link를 자기자신으로 가르키게 할 수는 없다. 이 경우엔 2번 노드에 연결하여 짝수 팰린드롬을 만드는 방향으로 진행해야 한다.
아래는 위의 구축 방법의 pseudo code 이다.
s = string
cnt = 2
last = 2
tree = [ { length, suffix_link, link} ]
make_node(position, ch):
cur = last
while position - tree[cur].length - 1 < 0 || s[position - tree[cur].length - 1] != ch:
cur = tree[cur].suffix_link
if ch exist tree[cur].link:
last = tree[cur].link[ch];
return
cnt += 1
last = tree[cur].link[ch] = cnt;
tree[last] = { tree[cur].length + 2, 1, map };
if tree[last].length == 1:
return
do:
cur = tree[cur].sufflink
while position - tree[cur].length - 1 < 0 || s[position - tree[cur].length - 1] != ch
tree[last].suffix_link = tree[cur].nxt[ch]
main():
tree[0] = NULL
tree[1] = {-1, 1, map}
tree[2] = { 0, 1, map}
s = input()
for i in 0 to length(s) - 1:
make_node(i, s[i]);
구현
위의 pseudo code를 기반으로 C++로 구현한 것이다.
#include <cstdio>
#include <map>
using namespace std;
struct node {
int len;
int sufflink;
map<char, int> nxt;
};
char o[200010];
int cnt = 2;
int lastsuff = 2;
node tree[200010];
void make_node(char c, int pos) {
int cur = lastsuff;
while(1) {
if(pos - tree[cur].len - 1 >= 0 && c == o[pos - tree[cur].len - 1]) break; // 만약 palindrome 을 만들 수 있다면
cur = tree[cur].sufflink; // 그렇지 못한경우 suffix link를 타고 간다.
}
if(tree[cur].nxt.count(c)) { // 만약 link에 해당하는 char가 존재한다면
lastsuff = tree[cur].nxt[c]; // last를 바꾼다.
return;
}
int nxt = lastsuff = tree[cur].nxt[c] = ++cnt; // 새로운 노드를 만들어낸다.
tree[nxt].len = tree[cur].len + 2; // 길이를 구한다.
if(tree[nxt].len == 1) { // 만약 길이가 1이라면
tree[nxt].sufflink = 2; // 2번 노드에 연결한다.
return;
}
while(cur > 1) {
cur = tree[cur].sufflink;
if(pos - tree[cur].len - 1 >= 0 && c == o[pos - tree[cur].len - 1]) { // 만약 palindrome을 만들 수 있다면
tree[nxt].sufflink = tree[cur].nxt[c]; // 해당 palindrome에 해당하는 노드에 연결한다. 이는 반드시 존재한다.
break;
}
}
}
int main() {
tree[1] = {-1, 1, map<char, int>()};
tree[2] = { 0, 1, map<char, int>()};
scanf("%s", o);
for(char *k = o; *k != '\0'; k++) make_node(*k, (int)(k - o));
}
주석으로 설명을 대체하도록 하겠다.
시간복잡도
Correctness를 증명하는 것은 이 포스트를 읽는이의 도전으로 남겨두고 싶다. 힌트를 하나 주자면 KMP의 Correctness를 증명하는 것과 거의 유사하다. 다만 시간복잡도가 $O(n)$ (만약, map을 사용했다면 $O(n log \alpha))$)인 것을 설명하자면, last가 늘어나는것은 1 뿐이지만 suffix_link를 타고 가는 것이 음수가 될수는 없으므로 while문은 최대 n번씩 밖에 돌 수 없다. 즉, 시간복잡도는 $O(n)$ 이다.
문제풀이
팰린드롬
이 링크를 통하여 문제에 접근할 수 있다. 이 문제는 어떤 문자열에서 부분 문자열중 팰린드롬인것이 출현한 횟수에서 그 팰린드롬의 길이를 곱한 값 중 제일 큰 값을 구하는 매우 간단한 문제이다. 이를 해결 하기 위해서는 manacher’s Algorithm 과 Suffix Array 그리고 Segment Tree를 사용하면 해결 할 수 있으나, 저 두가지의 자료구조를 구현 하는 것이 매우 매우 어렵기 때문에 Palindromic Tree 를 구현하여 해결하는 방법을 소개하고자 한다. 먼저 palindromic tree를 만들면서 노드에 방문할때마다, 혹은 생성될 때 마다 카운트 해준다. 이때, 현재 카운트 된 개수는 suffix link에 해당하는 노드에 영향을 주므로, 즉, suffix palindrome도 증가해야 하므로, 모두 만들고 나서 for문을 역으로 돌리면서 카운트된 개수를 다시 갱신해 주면 모든 palindrome에 대해서 값을 구할 수 있게 된다. 시간 복잡도는 당연하게도 $O(n)$
아래는 정답 코드이다.
#include <cstdio>
#include <map>
using namespace std;
struct node {
int len;
int sufflink;
map<char, int> nxt;
};
int cnt = 2;
int lastsuff = 2;
node tree[300010];
char o[300010];
int table[300010];
void make_node(char c, int pos) {
int cur = lastsuff;
while(1) {
if(pos - tree[cur].len - 1 >= 0 && c == o[pos - tree[cur].len - 1]) break;
cur = tree[cur].sufflink;
}
if(tree[cur].nxt.count(c)) {
lastsuff = tree[cur].nxt[c];
table[lastsuff]++; // 원래 있었으므로 1 카운트
return;
}
int nxt = lastsuff = tree[cur].nxt[c] = ++cnt;
tree[nxt].len = tree[cur].len + 2;
table[lastsuff]++; // 새로 만들어지면서 1 카운트
if(tree[nxt].len == 1) {
tree[nxt].sufflink = 2;
return;
}
while(cur > 1) {
cur = tree[cur].sufflink;
if(pos - tree[cur].len - 1 >= 0 && c == o[pos - tree[cur].len - 1]) {
tree[nxt].sufflink = tree[cur].nxt[c];
break;
}
}
}
long long ans = 0;
int main() {
tree[1] = {-1, 1, map<char, int>()};
tree[2] = { 0, 1, map<char, int>()};
scanf("%s", o);
for(char *k = o; *k != '\0'; k++) {
make_node(*k, (int)(k - o));
}
for(int i = cnt; i > 2; i--) { // 역순으로 돌면서
ans = max(ans, (long long)table[i] * tree[i].len); // 가장 끝 노드는 이미 계산이 완료 된 것이므로 정답 후보에 넣는다.
table[tree[i].sufflink] += table[i]; // suffix_link 에 해당하는 노드에 값 전파
}
printf("%lld\n",ans); // 정답 출력
}
The Problem to Slow Down You
이 링크를 통하여 문제를 볼 수 있다. 이 문제는 두개의 문자열이 주어졌을 때, 서로 같은 팰린드롬인 부분문자열의 쌍의 개수(이때 위치가 다르면 서로 다른것으로 센다.)를 구하는 문제이다. 이 문제는 푸는 방법이 두 가지가 있지만 KMP처럼 Palindromic Tree를 사용하는 방법을 보여주기 위해, 즉, 오토마타 처럼 사용하는 풀이를 보여주도록 하겠다. 일단 위의 팰린드롬 문제 처럼 Palindromic Tree를 구축한 뒤, 카운팅을 모두 완료시킨 상태에서 두번째 문자열을 오토마타로 읽듯이 훑어보는 과정이 필요하다. 하지만 여기서 중요한 것은 어떤 팰린드롬이 존재함을 감지했다면, 그것을 suffix link로 가지고 있는 모든 노드들에 값을 다시 전파해야한다. 즉, 이번엔 역순으로 카운트한 배열을 다시 정순으로 전파하는 작업을 해야한다. 그 작업을 완료한 뒤, 훑으면서 팰린드롬을 발견할 때 마다 우리가 정순으로 전파한 값을 더해나가면 쉽게 풀 수 있다.
시간 복잡도는 정말 당연하게도 $O(n)$ 이다.
아래는 정답 코드이다. 주석으로 자세히 설명하겠다.
#include <cstdio>
#include <map>
using namespace std;
struct node {
int len;
int sufflink;
map<char, int> nxt;
};
int cnt;
int lastsuff;
node tree[200010];
char o[200010];
char u[200010];
int table[200010];
long long sub[200010];
void make_node(char c, int pos) {
int cur = lastsuff;
while(1) {
if(pos - tree[cur].len - 1 >= 0 && c == o[pos - tree[cur].len - 1]) break;
cur = tree[cur].sufflink;
}
if(tree[cur].nxt.count(c)) {
lastsuff = tree[cur].nxt[c];
table[lastsuff]++;
return;
}
int nxt = lastsuff = tree[cur].nxt[c] = ++cnt;
tree[nxt].len = tree[cur].len + 2;
table[lastsuff]++;
if(tree[nxt].len == 1) {
tree[nxt].sufflink = 2;
return;
}
while(cur > 1) {
cur = tree[cur].sufflink;
if(pos - tree[cur].len - 1 >= 0 && c == o[pos - tree[cur].len - 1]) {
tree[nxt].sufflink = tree[cur].nxt[c];
break;
}
}
}
int main() {
tree[1] = {-1, 1, map<char, int>()};
tree[2] = { 0, 1, map<char, int>()};
int t, f = 0;
scanf("%d",&t);
while(t--) {
lastsuff = 2;
cnt = 2;
scanf("%s", o);
scanf("%s", u);
for(char *k = o; *k != '\0'; k++) make_node(*k, (int)(k - o));
long long ans = 0;
for(int i = cnt; i > 2; i--) table[tree[i].sufflink] += table[i]; // 역순 전파
for(int i = 3; i <= cnt; i++) { // 정순으로 다시 전파
sub[i] = table[i];
sub[i] += sub[tree[i].sufflink];
}
int now = 1;
for(char *k = u; *k != '\0'; k++) {
int flag = 0;
int pos = (int)(k - u);
while(pos - tree[now].len - 1 < 0 || u[pos - tree[now].len - 1] != *k || tree[now].nxt.count(*k) == 0) { // KMP 돌리듯이 타고 간다.
if(now == 1) {
flag = 1; // 만약 더이상 타고갈 suffix link가 없다면 위 문자열에선 없는 문자이므로 무시하기 위해 flag를 세운다.
break;
}
now = tree[now].sufflink;
}
if(flag) continue;
now = tree[now].nxt[*k]; // 이동
ans += sub[now]; // 정답을 더해준다.
}
for(int i = cnt; i > 2; i--) {
sub[i] = 0;
table[i] = 0;
tree[i].nxt.clear();
tree[i].len = 0;
tree[i].sufflink = 0;
}
tree[1].nxt.clear();
tree[2].nxt.clear();
table[2] = table[1] = 0;
printf("Case #%d: %lld\n", ++f, ans);
}
}
마무리
이번 포스트를 계기로 많은 사람들이 Palindromic Tree에 대해 이해하고 무난하게 사용할 수 있게 되었으면 좋겠다. 그리 좋은 글 솜씨는 아니지만 최대한 이해하기 쉽게 써보았으며, 많은 사람들이 Palindromic Tree를 활용하여 팰린드롬 문제를 대응할 수 있게 되었으면 좋겠다.
참고자료
- adilet.org; Palindromic Tree. Adilet Zhaxybay