빠른 격자점 세기
서론
우리는 어떤 그래프 내부의 격자점을 세어야 할 일이 있는 경우가 있다. 예를 들면, 원 안의 격자점의 갯수를 세는 것은 $\pi$ 의 값과 피타고라스 쌍과 관련이 있으며, 약수의 갯수의 합을 구하려 $f(x) = \frac{N}{x}$ 내부의 격자점의 수를 세기도 한다. 여기서는 이 전략을 구체화 시켜서 convex hull 위의 점의 갯수로 문제를 푸는 방법에 대해 알아보고, 또한 약수의 갯수를 $\tilde{O}(n^{\frac{1}{3}})$ 에 세는 방법을 알아본다.
약수
두 자연수 $A$, $B$에 대해서 $B$로 $A$를 나눴을 때 나누어 떨어지면, 우리는 $B$를 $A$의 약수라고 한다. 예를 들면, 6을 2로 나누면 몫이 3이고, 나머지가 없기 때문에 2는 6의 약수이다. 하지만, 6을 5로 나누면 몫은 1, 나머지가 1이기 때문에 5는 6의 약수가 아니다.
우리는 1 이상 $N$ 이하의 모든 수에 대해서 약수의 갯수의 합을 구하는 문제를 푸려고 한다. 예를 들면, 1은 약수가 한개, 2는 약수가 2개, 3은 약수가 2개, 4는 약수가 3개, 5는 약수가 1개, 6은 약수가 4개 있으므로, 1 이상 6 이하의 수의 약수의 갯수를 모두 더하면 15이다.
Naive
약수를 구하는 가장 쉬운 방법은 1이상 $N$ 이하의 수로 모두 나눠 보는 것이다. 그러면, 총 $O(N^2)$ 의 시간으로 문제를 풀 수 있다.
우리는 약수를 $O(\sqrt{N})$ 시간 안에 구할 수 있는 방법을 잘 알고 있다. 이는 $\sqrt{N}$ 이하의 수로만 나눠 보는 것이다. 어떤 $N$의 약수 $a$가 만족하는 조건은, 다른 약수 $b$가 존재하여 $N=ab$를 만족하는 것이고, $a$와 $b$ 중 하나는 $\sqrt{N}$ 보다 작거나 같고, 어느 하나는 크거나 같기 때문에, 작거나 같은 것의 갯수만 세어주어 두배 하면 되고, $a=b$인 경우만 예외를 잘 처리해 주면 된다. 이 경우 총 $O(N \sqrt{N})$시간으로 문제를 해결할 수 있다.
여기서 더 시간 복잡도를 개선하기 위해서는, 우리는 특정한 수의 약수를 굳이 셀 필요가 없이 전체적으로 세면 된다는 관찰이 필요하다. 숫자 $a$를 약수로 하는 수는, $a$의 배수이다. 즉 어떤 수가 약수로 등장하는 횟수는, $N$이하의 수 중 $a$의 배수의 갯수이고 이는 $\lfloor \frac{N}{a} \rfloor$로 구할 수 있다. 우리가 구해야 하는 후보는 $a$ 가 1 이상 $N$이하인 $a$이기 때문에, $\sum_{i=1}^{N} \lfloor \frac{N}{i} \rfloor$ 이 1 이상 $N$이하의 약수의 갯수이다. 이것을 바로 계산하면 $O(N)$ 시간에 문제를 해결할 수 있다.
우리는 이것이 결국에는, 그래프 $f(x) = \frac{N}{x}$ 아래의 격자점의 갯수라는 사실을 알 수 있다. 이 격자점의 분포에는 큰 특징이 있는데, $y = x$ 직선을 기준으로 대칭이라는 것이다. 그래서 $k =\lfloor\sqrt{N} \rfloor$ 에 대해서, 1 이상 $k$ 이하인것만 더하고, 중복된 아래 정사각형 부분을 빼 주는, 즉 $2\sum_{i=1}^{k} \lfloor \frac{N}{i} \rfloor - k^2$ ($k = \lfloor \sqrt{N} \rfloor$) 이 바로 1이상 $N$ 이하의 약수의 갯수이다. 이는 간단하게 $O(\sqrt{N})$ 시간에 구할 수 있고, 이것이 우리의 Naive 알고리즘이다.
볼록/오목함수와 Convex Hull
우리는 볼록/오목함수가 가지는 특징에 대해 알아볼 것이다. 볼록/오목함수의 정의는 $(x, f(x))$ 와 $(y, f(y))$ 를 잇는 선분을 그었을 때, 선분 전체가 함수 아랫쪽에 위치하면 볼록함수, 위쪽에 위치하면 오목함수이다.
이런 함수들에 대해서, 우리는 Convex Hull을 생각할 것이다. 여기서는 오목함수를 생각하자. $y = f(x)$ 에 대해서, 우리는 격자점의 수를 세어야 하기 때문에 $(x, \lfloor f(x) \rfloor)$를 생각할 것이다. 이것을 모두 포함하는 Convex Hull을 만들면, 아래쪽선분이 다음 그림과 같이 나오고, 우리가 사다리꼴의 점 갯수와 비슷하게 점들을 셀 수 있다는 것을 알 수 있다.
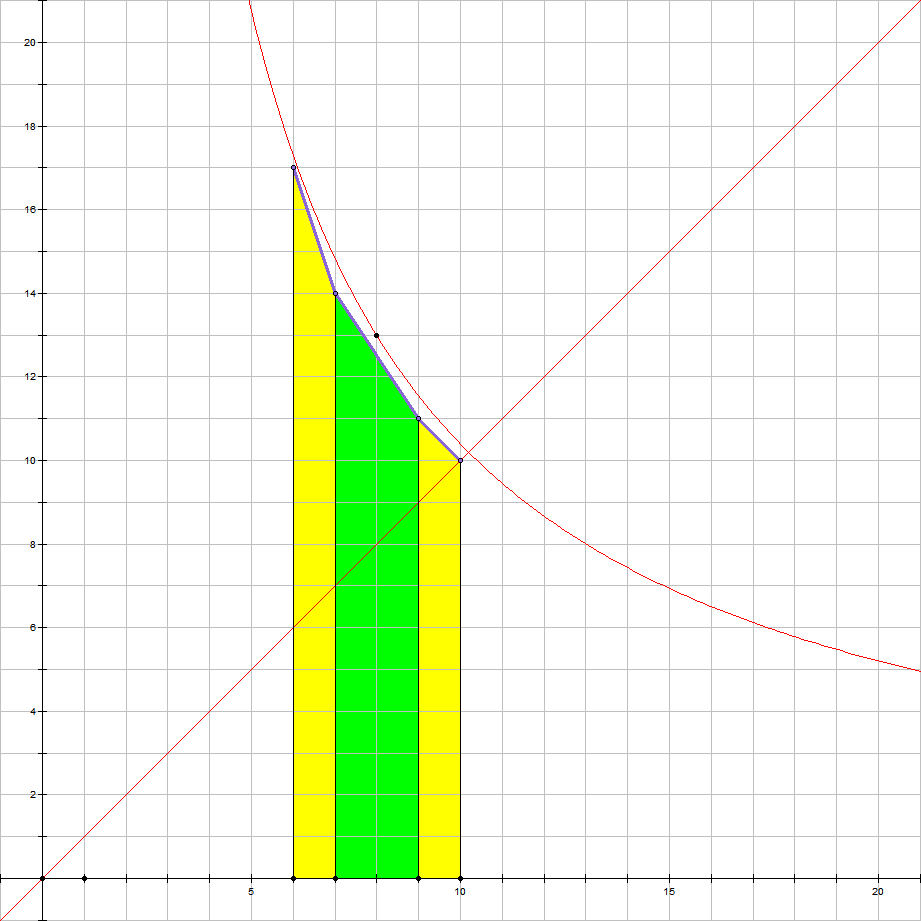
Convex Hull에 포함되지 않는 모든 점 (a, \lfloor f(a) \rfloor)에 대해서, (a, \lfloor f(a) \rfloor-1) 은 이 밖에 있음을 증명할 수 있다. (사다리꼴 내부는 Convex Hull 밖이다) 이 경우, 우리는 나눠진 사다리꼴 안의 격자점의 수를 세어 주고, Convex Hull 에 포함되지 않는 점들의 갯수를 추가적으로 세어주면, 전체적으로 격자점의 갯수를 셀 수 있다.
격자점의 갯수를 세는 것은 $(x_1 - x_0 - 1)(y_0 +y_1- 1)/2$ 이고, 이는 사다리꼴의 면적 공식 등으로도 간단하게 구할 수 있다. 포함되지 않는 격자점과 오른쪽 격자점은 각각 $(x_1-x_0-1)$개와 $y_1$개 이므로, 이것을 모든 사다리꼴 값마다 누적시켜주면 된다.
결론적으로, 우리가 Convex Hull을 구하기만 하면 문제는 Convex Hull의 점의 갯수 시간복잡도로 해결할 수 있음을 알 수 있다.
Convex Hull 구하기
Convex Hull 위에 있는 점들을, Convex Hull 위의 점의 갯수에 비례하는 시간복잡도로 구할 수 있다. Convex Hull 위에 있는 점은 원의 경우에 $O(N^\frac{2}{3})$이고, $y = \frac{N}{x}$ 의 경우에는 $\tilde{O}(N^\frac{1}{3})$이다.
결국 우리는 결국 어떤 점을 찾을 때 어떤 기울기(의 절댓값)에 대해서, 이 기울기가 $ \mid f’(x) \mid $ 이상이면서, $f(x)$ 의 아래쪽에 존재하는 가장 기울기가 가파른 점을 찾고 싶은것이다.
즉, 이것을 Stern-brocot tree를 이용해서 이진탐색을 하면 되며, 기존 점이 $(x_0, y_0)$ 일 때, 새 점을 구하는 유사코드는 다음과 같다.
a, b, c, d = 0, 1, 1, 0 # a/b <= slope < c/d
while True:
p, q = a+c, b+d # child in stern-brocot tree
x1, y1 = x0+q, y0-p
if x1 <= K and (y1+1)*x1 > N: # Not included
a, b = p, q
elif N/a <= b/(x1**2): # real division
x1, y1 = x+b, y-a # maximum possible slope
break
else:
c, d = p, q
결론
위의 사항을 모두 종합하면 $\tilde{O}(N^\frac{1}{3})$에 약수의 갯수를 구할 수 있다. 이것 이외에도, 원 안에 격자점을 세는 등, 임의의 완만하고 볼록 혹은 오목인 함수에서 모두 사용할 수 있다.