wwiiiii's profile image

wwiiiii

August 18, 2019 18:30

Goals

본 논문은 “Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor” 논문의 확장판으로, continuous action space 환경에서 동작하는 off-policy 알고리즘인 SAC를 소개합니다. 주된 목표는 다음과 같습니다.

1. Off-policy 알고리즘을 통한 sample inefficiency 해결

   On-policy 알고리즘의 경우 업데이트에 쓰이는 데이터가 항상 현재 학습 대상인 policy에서 생성되어야 하기 때문에 한번 사용한 데이터는 다시 쓰지 못하는 단점이 있습니다.

2. Objective에 Entropy term을 추가를 통한 near-optimal policy 고려와 exploration 능력 향상

   Policy의 엔트로피가 클수록 특정 행동의 확률이 매우 높아지기보단 모든 action의 확률이 비슷하게 됩니다. 각 action이 선택될 확률 분포가 더 평평하다고 생각할 수도 있습니다. 따라서 엔트로피를 증가시키는 방향으로 objective를 설정하면 더 다양한 action을 선택하게 될 것이고, 더 나은 exploration을 기대할 수 있습니다.

   또 다른 효과로는 optimal action에 비해 크게 낮지는 않은 sub-optimal action이 있을 때 해당 action도 자주 선택되도록 하여 sub-optimal solution 또한 같이 학습할 수 있도록 합니다. 학습 환경과 테스트 환경이 다른 경우 optimal solution이 후자에서 동작하지 않을 수 있는데, sub-optimal solution도 잘 학습해두었기 때문에 학습이 완료된 Agent가 테스트 환경에서도 더 robust하게 동작함을 기대할 수 있습니다.

3. 여러 환경에서 하이퍼파라미터 튜닝없이 Robust하게 작동할 수 있도록 Entropy Coefficient 자동 결정

   과거 SAC 논문에서는 위의 Entropy term을 추가할 때 기존의 Reward-based objective와 Entropy 간 중요도를 Entropy term에 하이퍼파라미터를 곱하는 것으로 나타내었는데, 이 하이퍼파라미터가 문제 환경에 따라 민감해 튜닝이 필요했습니다. 확장판 논문에서는 하이퍼파라미터 $ \alpha $ 를 자동으로 조정하는 부분이 추가되었습니다.

특기할 점은 다음과 같습니다.

• (1)과 (2)의 경우 SAC의 조상이라고 할 수 있는 Soft Q-learning에서 이미 해결한 문제입니다. 아래에 쓰인 Differences에서 SAC가 SQL 대비 어떤 다른 장점이 있는지 볼 수 있습니다.

논문의 자세한 내용은 아래에서 소개하도록 하겠습니다.

Differences

본 논문과 가까운 접근 순으로 어떤 점이 다른지 비교해보겠습니다. 몇몇 부분이 잘 이해되지 않을 경우 아래 Method에 설명된 본 논문 내용을 읽은 후 돌아오는 것도 좋습니다.

Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor

https://arxiv.org/abs/1801.01290

Goals에서 설명한 바와 같이 원본 SAC에서는 엔트로피의 기여도를 하이퍼파라미터로 두었는데, 본 확장판 논문에서는 이를 자동적으로 최적화하는 방법을 제시합니다. 자세한 내용은 Method의 Automating Entropy Adjustment 부분에서 설명하겠습니다.

Reinforcement Learning with Deep Energy-Based Policies (Soft Q-learning, SQL)

https://arxiv.org/abs/1702.08165

SAC의 직계 조상으로 볼 수 있는 논문입니다. SQL의 내용을 간단히 요약하면 다음과 같습니다.

$\mathcal{H}$ 를 엔트로피 함수로 정의했을 때, $ \pi^* \propto exp \space Q(s, a)$ 를 만족하게 policy를 정의하면 해당 policy는 maximum-entropy RL objective의 optimal solution이 됩니다. 즉, 아래의 식이 성립하게 됩니다.

\[\pi^* = \underset{\pi}{argmax} \space \mathbb{E}_\pi [\sum_{t=0}^T r_t + \mathcal{H(\pi(\cdot|s_t))} ]\]

또한 기존 Q-learning의 업데이트 식을 아래와 같이 바꾸면, maximum-entropy RL objective에 대한 optimal Q 함수를 학습할 수 있습니다.

\[Q(s_t, a_t)=\mathbb{E}[r_t+\gamma \mathrm{softmax}_aQ(s_{t+1},a)] \\ \mathrm{softmax}_a f(a) := log \int exp f(a)da\]

(2)의 식을 살펴보면 우리가 원래 알고 있던 bellman equation 에서 max 만 softmax 로 바뀐 것을 알 수 있습니다. 이 Soft bellman equation도 원래 bellman equation처럼 contraction operator이고, optimal Q 함수가 해당 식을 만족시키기 때문에 Q-learning과 같은 방법으로 학습을 진행하면 optimal Q 함수를 얻을 수 있습니다. 더 자세한 내용은 저자의 블로그 를 참고하시면 됩니다.

SAC는 근본적으로 위의 내용에 Actor-Critic 세팅을 적용한 것입니다. Objective에 엔트로피 항을 추가한다는 기본적인 방향은 동일하지만, SAC는 SQL에 비해 몇가지 장점을 더 갖습니다.

1. Q-learning이나 Soft Q-learning에서는 Optimal Q, Optimal V 함수를 학습하게 됩니다. 이 경우 계산 과정에서 (soft)max operator와 expectation이 둘 다 등장하게 되는데, 아래의 이유 때문에 biased estimation이 됩니다(유명한 Double Q-learning이 다루는 문제이기도 합니다)¹.

   $ Q(s, a) \leftarrow r(s, a) + \gamma \space \underset{a’}{\mathrm{max}} \space \mathbb{E}{s’\sim p(s’|s, a)}[Q(s’, a’)]
   \le r(s, a) + \gamma \space \mathbb{E}{s’\sim p(s’|s, a)}[\underset{a’}{\mathrm{max}}\space Q(s’, a’)] $

   하지만 SAC에서는 현재 policy의 Q, V 함수를 계산해서 사용하기 때문에 (soft)max operator가 사용되지 않고, 단순히 sampling으로만 계산해도 bias가 발생하지 않아 더 안정적인 학습을 기대할 수 있습니다.

2. SQL은 policy를 따로 계산해두지 않고 exp Q 를 따르는 분포를 사용하는데, 이는 intractable하기 때문에 이 분포에서 action을 sampling하기 위해 MCMC나 Stein variational gradient descent와 같은 추가적인 계산이 필요합니다. 반면 SAC는 policy를 직접적으로 근사하는 function approximator를 사용하기 때문에 이와 같은 문제에서 자유롭고, 계산복잡도에서 이득을 보게 됩니다.

SQL과 비교했을 때 SAC는 엔트로피를 사용하자는 기본 골자는 그대로 유지하며 Actor-Critic 세팅의 장점을 취한 것을 알 수 있습니다.

기타 Policy Gradients & DQN 계열 (A3C, ACER, Q-learning, …)

사실 Exploration을 잘하기 위해 Entropy를 사용하자는 아이디어 자체는 SQL이나 SAC에서 처음 나온 것은 아닙니다. 2016년도에 나온 유명한 A3C의 경우도 policy의 negative entropy를 loss항에 더하면 실험적으로 exploration이 잘 된다고 언급하고 있습니다. A3C과 같은 on-policy 알고리즘은 (behavior policy가 target policy와 달라지기 때문에 on-policy 가정이 깨지므로) $ \epsilon$-greedy를 쉽게 사용할 수 없기 때문에, 후속 논문들에서도 그 대체재로 엔트로피를 이용한 휴리스틱이 많이 사용되고 있습니다². 다만 SAC의 경우 휴리스틱 기반의 regularization으로 도입한 것이 아니라, 아예 objective에 엔트로피 항을 넣는다는 관점의 차이가 있습니다.

또 한가지 중요한 차이점은, 대부분 policy gradient 알고리즘의 policy improvement는

1. initial state의 value를 objective로 삼고
2. 이를 증가시키는 방향의 그래디언트를 estimation해
3. 해당 그래디언트를 사용해 업데이트를 진행

으로 이루어지는데, 보통 (2)의 과정에서 “업데이트에 사용되는 state-action pair에 대해 해당 action이 target policy의 분포를 따라야 한다” 라는 조건이 붙기 때문에 과거 데이터를 사용하기 위해선 importance sampling 등의 추가 보정 작업이 필요합니다. 또 그 과정에서 ratio 값의 범위에 제한이 없으면 학습이 불안정해지기 때문에 여러 테크닉을 통해 bound 해주는 등 보정 작업을 거쳐야 off-policy 알고리즘으로 사용할 수 있습니다.

그런데 SAC의 경우 policy improvement 과정이

1. 현재 policy에 대한 Q 함수의 estimation을 기반으로 policy를 exp Q에 비례하게 업데이트

만으로도 improvement가 이루어지며, 업데이트에 필요한 Q 함수의 학습은 기존의 Q-learning과 동일한 off-policy 알고리즘³으로 진행되기 때문에 추가적인 보정 작업 없이 자연스럽게 off-policy 알고리즘이 됩니다. 따라서 구현 난이도가 다른 off-policy policy gradient 접근에 비해 꽤 낮은 편입니다.

Method

원 논문의 구성과 같이

1. 논문의 핵심 아이디어
2. Tabular 세팅에서의 접근
3. 실제 환경에서 Practical하게 사용할 수 있는 방법
4. Entropy coefficient 하이퍼파라미터 자동 조정

순으로 내용을 정리해보도록 하겠습니다.

아이디어를 설명하기에 앞서, 흔히 사용되지는 않는 notation이 있어 하나만 짚고 넘어가겠습니다.

$ \rho_\pi(s_t) $ 와 $ \rho_\pi(s_t, a_t)$ 라는 notation이 있는데, 각각 $ \pi(a_t|s_t) $ 를 따랐을 때 state와 state-action의 marginal distribution 입니다. 즉 $ s \sim \rho_\pi(s_t) $ 라고 적으면 $ s $ 는 $ \pi $ 를 따라 행동했을 때 결과적으로 관측하게 되는 t번째 상태의 분포를 따른다는 뜻입니다.

아이디어

보통 강화학습의 objective는 보상의 누적합 $ \sum_t \mathbb{E}{(s_t,a_t) \sim \rho\pi}[r(s_t, a_t)]$ 을 최대화하는 것이고, 이를 위해 주어진 상태에서 어떤 행동을 할지 결정하는 policy $\pi : S \times A \rightarrow [0, 1] $ 를 학습시키게 됩니다.

여기에 policy의 엔트로피를 증가시키자는 목표를 추가한 것을 Maximum entropy objective라 부릅니다. 이를 수식으로 나타내면 다음과 같습니다.

\[\underset{t}{\sum}\mathbb{E}_{(s_t, a_t) \sim \rho_\pi}[r(s_t, a_t)+\alpha \mathcal{H}(\pi(\cdot|s_t))]\]

여기서 $ \mathcal{H} $ 는 통상적으로 사용되는 엔트로피 함수이고, $ \alpha $ 는 보상과 엔트로피의 상대적 중요도를 결정하는 하이퍼파라미터입니다.

엔트로피 증가를 목표항에 도입시키면 다음과 같은 장점이 있습니다.

1. 서로 다른 행동을 선택할수록 엔트로피가 높아지기 때문에 Exploration이 더 이루어집니다. 보상의 합도 같이 고려하기 때문에 기대 보상이 많이 낮은 행동을 시도할 위험도 적습니다.

2. Q-learning과는 다르게 비슷한 기대값을 가진 여러개의 near-optimal policy가 있을 경우, 학습 과정에서 near-optimal action 각각을 모두 고려하게 됩니다. Maximum entropy objective의 optimal policy는 exp Q에 비례하는 것을 생각하면 직관적으로 이해하기 쉽습니다⁴.

   

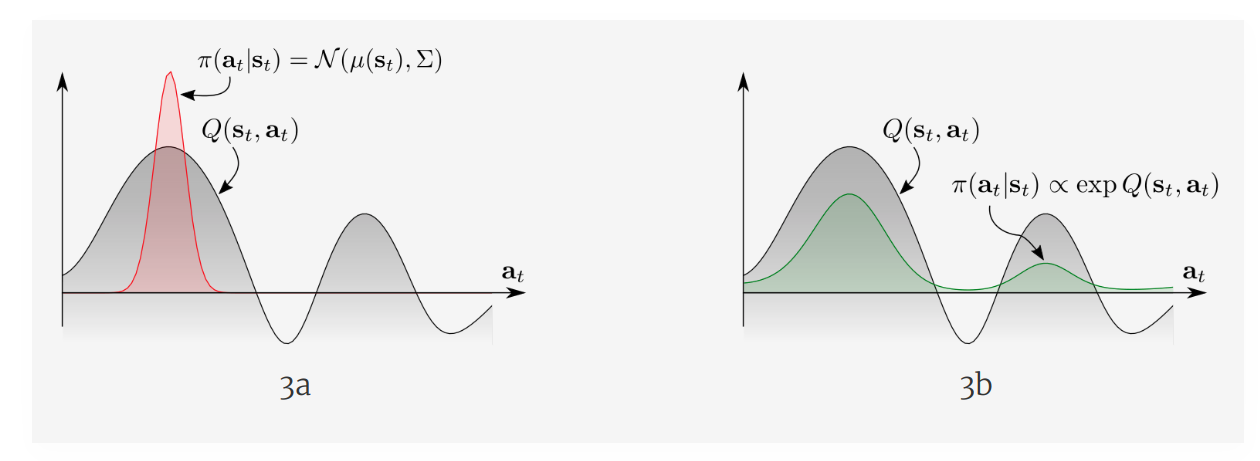
실제 실험을 진행해봐도 Exploration이 잘 이뤄져 학습 속도가 빨라진다고 합니다.

Soft Policy Iteration

이제 이론적으로 위의 objective를 만족하는 policy를 어떻게 학습할지 살펴보겠습니다. 여기서 이론적이라는 말의 뜻은 tabular 세팅을 가정한다는 의미입니다.

기본적인 골자는 Policy Iteration입니다. 현재 policy $ \pi $ 에 대한 Soft Q 함수 $ Q_\pi $ 를 학습하는 Policy Evaluation 단계와, 학습한 $ Q_\pi $ 를 바탕으로 $ \pi$ 보다 더 좋은 새로운 policy $ \pi’$ 를 찾는 것을 반복해 optimal policy $ \pi^*$를 찾게 됩니다.

$ Q $ 의 학습은 기존 Q-learning과 거의 똑같이 이루어집니다. Bellman backup operator $ \mathcal{T}^\pi$ 를 정의하면,

\[\mathcal{T}^\pi Q(s_t, a_t) \leftarrow r(s_t, a_t) + \gamma \space \mathbb{E}_{s_{t+1}\sim env}[V(s_{t+1})]\]

과 같이 $ Q $를 업데이트 할 수 있습니다. 여기서 $ V $ 또한 optimal value function이 아닌 현재 policy에 대한 value function 이므로 다음 식이 만족됩니다.

\[V(s_t) = \mathbb{E}_{a_t \sim \pi}[Q(s_t, a_t) - \alpha \space \mathrm{log}\space \pi(a_t|s_t)]\]

여기서 log 항은 $ \mathcal{H}(\pi) := \mathbb{E}_\pi [-\mathrm{log} \space \pi(a_t|s_t)] $ 임을 활용해 엔트로피 항을 Expectation 안에 log 꼴로 넣은 것입니다.

이제 $ \pi $ 가 주어졌을 때 (5)의 업데이트를 계속 반복하면 $ \pi $ 에 대한 Soft Q function을 찾을 수 있습니다. ⁵

그 후 새로운 policy $ \pi_{new}$ 가 $ \mathrm{exp}$ $Q^{\pi_{old}}$ 를 따르도록 업데이트를 진행할 것인데, SQL과의 비교에서 살펴본 것과 같이 exp Q 에 비례하는 분포는 intractable 합니다. 대신 우리가 사용 가능한 꼴의 policy parametrization space로 exp Q를 projection 한 결과를 $ \pi_{new} $ 로 사용하면 이런 문제점을 우회할 수 있습니다. 가장 널리 쓰이는 KL Divergence를 도입하면 다음과 같이 됩니다.

\[\pi_{new} = \underset{\pi' \in \Pi}{\mathrm{argmin}}\space D_{KL}(\pi'(\cdot|s_t)||\frac{exp(\frac{1}{\alpha}Q^{\pi_{old}}(s_t, \cdot))}{Z^{\pi_{old}}(s_t)})\]

여기서 $ Z $ 는 분자를 위한 normalization term인데, 실제로는 intractable 한 값이지만 나중에 Gradient Descent로 $ \pi $ 를 업데이트할 경우 무시해도 되기 때문에 intractable 하다는 문제를 우회할 수 있습니다.

놀라운 사실은 exp Q 자체가 아니라, exp Q에 가깝지만 여전히 tractable한 꼴로 나타내기 위해 projection이란 방법을 사용해 만든 새로운 policy $ \pi_{new} $ 도 원래 policy $ \pi_{old} $ 보다 좋다는 것⁶이 보장되기 때문에 항상 Policy Improvement가 이루어진다는 것이 보장됩니다. 증명의 대략적인 방향은 argmin operator를 사용하므로 KL div 값은 항상 $ \pi_{new} $ 가 $ \pi_{old}$ 보다 작거나 같게 되고, 이로부터 $ Q $ 간의 부등식을 유도하는 것입니다.

이제 Evaluation과 Improvement를 반복하면 Optimal Policy를 찾을 수 있습니다.

Soft Actor-Critic

그런데 위의 알고리즘을 실제 환경에서 그대로 구현해서 쓸 수는 없습니다. Continuous action space 이기 때문에 모든 state-action pair를 고려할 수 없고, discrete라고 해도 evaluation이 수렴하기 기다리는 것과 improvement의 해를 찾는 과정이 필요하기 때문입니다. 따라서 function approximtor를 통해 Q 함수과 policy를 표현하고, evaluation과 improvement를 각각 완벽하게 수렴할 때까지 기다리는 것이 아니라 stochastic gradient descent를 통해 번갈아가며 한번씩만 업데이트하는 근사 알고리즘을 사용할 것입니다.

Policy Evaluation, 즉 Q 함수를 위한 Optimization objective는 다음과 같습니다. $\bar{\theta}$ 는 DDPG와 같이 $\theta$ 의 moving average 입니다.

\[J_Q(\theta)=\mathbb{E}_{(s_t, a_t) \sim D}[\frac{1}{2}(Q_\theta(s_t, a_t) - (r(s_t, a_t)+\gamma \space \mathbb{E}_{s_{t+1} \sim env}[V_\bar{\theta}(s_{t+1})]))^2]\]

(6)에서 나온 $ V $ 의 정의에 따라, $ V $ 의 expectation은 $ a_{t+1}$ 을 현재 policy $\pi$ 에서 샘플링 한 후 (6)의 우변에 대입하는 것으로 계산할 수 있습니다. 일반적인 Replay Memory를 사용했다면 $ (s, a, s’) $ 가 $ s’ \sim env $ 를 따르게 저장되어 있을 것이기 때문에 기댓값은 동일하게 됩니다. 즉 아래 항을 최적화 대상으로 삼으면 됩니다.

\[J_Q(\theta)=\mathbb{E}_{(s_t, a_t) \sim D}[\frac{1}{2}(Q_\theta(s_t, a_t) - (r(s_t, a_t)+\gamma \space (Q_\bar{\theta}(s_{t+1}, a_{t+1})-\alpha \mathrm{log}(\pi_\phi(a_{t+1}|s_{t+1}))))^2]\]

각 항이 모두 미분가능하기 때문에 SGD를 사용할 수 있습니다.

이제 Policy Improvement를 위해, KL Divergence 항을 고려해봅시다. KL Divergence 항을 전개하면 아래와 같은 결과를 얻을 수 있습니다. ⁷

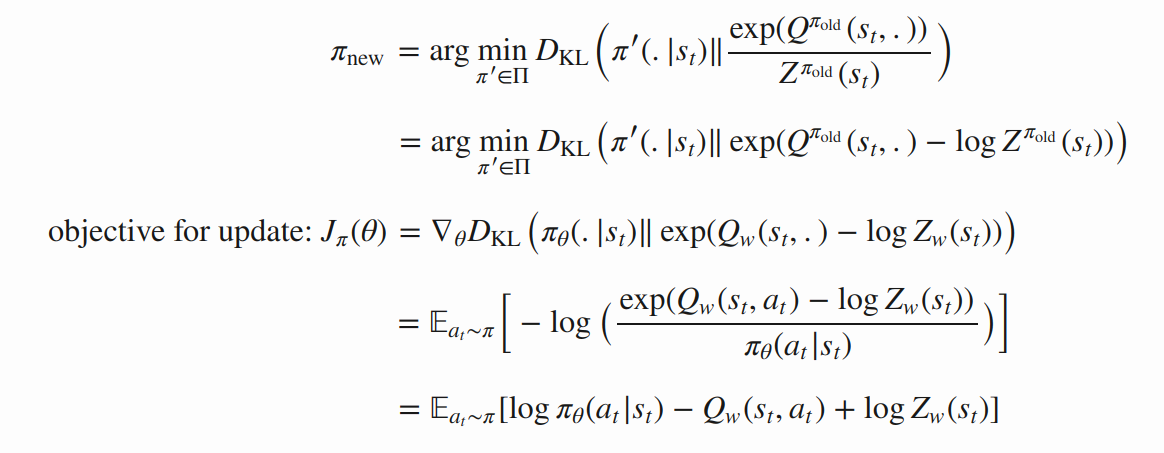
따라서 policy $ \pi $ 에 대한 Optimization Objective는 아래와 같이 나타낼 수 있습니다.

\[J_\pi(\phi)=\mathbb{E}_{s_t \sim D, a_t \sim \pi_\phi}[\alpha \mathrm{log}(\pi_\phi(a_t|s_t)-Q_\theta(s_t, a_t))]\]

마찬가지로 $ s_t $ 는 Replay Memory에서 샘플링하고 $ a_t $ 는 현재 policy에서 샘플링 해주면 각 항이 모두 미분 가능하기 때문에 SGD로 업데이트를 할 수 있습니다. 그런데 (10)의 식을 다시 써보면

\[J_\pi(\phi) =\mathbb{E}_{s_t \sim D}[-\alpha\mathcal{H}(\pi_\phi(\cdot|s_t))-\mathbb{E}_{a_t \sim \pi_\phi}[Q_\theta(s_t, a_t)]] \\ =-\mathbb{E}_{s_t \sim D}[\mathbb{E}_{a_t \sim \pi_\phi}[Q_\theta(s_t, a_t)]+\alpha\mathcal{H}(\pi_\phi(\cdot|s_t))]\]

가 되어 결과적으로는 DDPG와 비슷하게 Objectvie를 근사하는 함수를 학습한 후, 그 함수를 최대화하는 방향으로 SGD를 통해 policy를 학습한다고 이해할 수도 있습니다.

마찬가지로 reparameterization trick을 도입해 업데이트에 쓰일 action을 샘플링 한 후 노이즈를 추가해 variance를 줄일 수도 있습니다. TD3의 target policy smoothing과 유사한 테크닉으로 볼 수 있습니다.

Automating Entropy Adjustment

이때까지 엔트로피의 기여도를 나타내는 값 $ \alpha $ 는 하이퍼파라미터로 쓰였는데, 사실 태스크마다 보상의 스케일이 다를 뿐만 아니라 학습이 진행되면서 Policy의 엔트로피 값의 분포도 변하기 때문에 적절한 $ \alpha $ 의 값을 찾는 것은 쉽지 않은 문제입니다.

저자들은 대신 엔트로피 항을 Objective에 두는게 아니라 constraint로 뺀 후 contrained optimization problem으로 문제를 바꾸고, 이의 dual problem을 통해 dual variable $ \alpha $ 의 최적 해를 계산하는 식으로 접근합니다.

\[\underset{\pi}{\mathrm{max}}\space \mathbb{E}_{\rho_\pi}[\sum_{t=0}^T r(s_t, a_t)] \space s.t. \mathbb{E}_{(s_t, a_t) \sim \rho_\pi}[-\mathrm{log}(\pi_t(a_t|s_t))] \ge \mathcal{H} \space \forall t\]

Constraint 항을 좀 더 직관적으로 적으면 $ \mathcal{H_{\pi_t}} \ge \mathcal{H} $ 로 적을 수 있습니다. 엔트로피가 특정 값 이상이 되게 하는 policy 중 Reward Objective를 최대화시키는 policy를 찾는 문제라는 것을 알 수 있습니다.

우리가 다루는 환경은 MDP 이기 때문에, 특정 state에 도달하고 나면 그 때부터의 policy는 그 이전의 policy에 대해 영향을 받지 않습니다. 특정 state에 도달할 확률이야 이전 policy에 영향을 받겠지만, 도착하고 나서부터는 관련이 없기 때문에 위의 objective를 아래와 같이 쪼개서 생각할 수 있습니다. 부분 문제의 최적해를 계속 구해내는 것이 전체 문제의 최적해를 구성한다는 점에서 동적 계획법과도 비슷한 개념입니다.

\[\underset{\pi_0}{\mathrm{max}} ( \mathbb{E}[r(s_0, a_0)] + \underset{\pi_1}{\mathrm{max}}(\mathbb{E}[...] + \underset{\pi_T}{\mathrm{max}} \mathbb{E}[r(s_T, a_T)]))\]

그럼 맨 먼저 $ \underset{\pi_T}{\mathrm{max}} \space \mathbb{E}[r(s_T, a_T )]$ 부터 살펴봅시다. 주어진 constraint $ \mathcal{H_{\pi_T}} \ge \mathcal{H} $ 를 고려하면 dual problem은 다음과 같습니다.

\[\underset{\pi_T}{\mathrm{max}} \mathbb{E}_{(s_t, a_t) \sim \rho_\pi} [r(s_T, a_T)] = \underset{a_T \ge 0}{\mathrm{min}} \space \underset{\pi_T}{\mathrm{max}} \mathbb{E} [r(s_T, a_T) - \alpha_T \space log \space \pi(a_T|s_T)] - \alpha_T \mathcal{H}\]

Dual problem이 왜 이렇게 나오는지 익숙하지 않다면 $ h(\pi) = \mathcal{H_\pi} - \mathcal{H}$ , $ f(\pi) = \mathbb{E}[r(s_T, a_T)] $ if $ h(\pi) \ge 0$ else $ -\infty$ 로 두고 $ L(\pi, \alpha) = f(\pi) + \alpha h(\pi )$ 를 정의해, $ f(\pi) = \underset{\alpha \ge 0}{\mathrm{min}} L(\pi, \alpha) $ 인 사실에서 양변에 $ \mathrm{max} $ 를 씌우는 과정을 따라가보면 이해하기 쉽습니다⁸.

이제 Iterative 한 방식으로 주어진 초기 $ \alpha_T $ 에 대해 $\mathrm{max}_{\pi_T} $ 를 계산해 optimal policy $ \pi_T^$ 를 구하고, 다시 $ \pi_T^$ 에 대해 $ \underset{\alpha_T \ge 0}{\mathrm{min}} $ 을 계산해 optimal coefficient $ \alpha_T^*$ 를 구할 수 있습니다.

\[\underset{\alpha_T}{\mathrm{argmin}} \space \mathbb{E}_{s_t, a_t \sim \pi_t^*} [-\alpha_T \space log \space \pi_T^* (a_T|s_T;\alpha_T) - \alpha_T \mathcal{H}]\]

이제 $ Q $ 함수를 재귀적으로 나타내고

\[Q_t^*(s_t, a_t; \pi_{t+1:T}^*, \alpha_{t+1:T}^*) = \mathbb{E} [r(s_t, a_t)] + \mathbb{E}_{\rho_\pi} [Q_{t+1}^*(s_{t+1}, a_{t+1}) - \alpha_{t+1}^* \space log \space \pi_{t+1}^* (a_{t+1} | s_{t+1})]\]

$ T-1$ 번째 step에 대해 계산하면

\[\underset{\pi_{T-1}}{\mathrm{max}} \space (\mathbb{E} [r(s_{T-1}, a_{T-1})] \space + \space \underset{\pi_T}{\mathrm{E}}[r(s_T, a_T)]) \\ = \underset{\pi_{T-1}}{\mathrm{max}} (Q_{T-1}^*(s_{T-1}, a_{T-1})-\alpha_T \mathcal{H}) \\ = \underset{\alpha_{T-1} \ge 0}{\mathrm{min}} \underset{\pi_{T-1}}{\mathrm{max}} (\mathbb{E} [Q_{T-1}^*(s_{T-1}, a_{T-1})] - \mathbb{E}[\alpha_{T-1} \space log \space \pi(a_{T-1}|s_{T-1}] - \alpha_{T-1} \mathcal{H} ) + \alpha_T^* \mathcal{H}\]

위의 식과 같은 꼴의 업데이트가 수행되는 것을 볼 수 있습니다.

\[\alpha_t^* = \underset{\alpha_t}{\mathrm{argmin}} \space \mathbb{E}_{a_t \sim \pi_t^*} [-\alpha_t \space log \space \pi_t^*(a_t|s_t;\alpha_t) \space - \space \alpha_t \bar{\mathcal{H}}]\]

실제 Practical하게 사용할 땐 다음 Objective를 최소화시키는 방향으로 SGD를 통해 업데이트하면 됩니다.

\[J(\alpha) = \mathbb{E}_{a_t \sim \pi_t}[-\alpha \space \mathrm{log}\space \pi_t(a_t|s_t) - \alpha \bar{\mathcal{H}}]\]

직관적으로 다시 쓰면 다음과 같습니다.

\[J(\alpha) = \alpha(\mathcal{H}_{\pi_t} - \bar{\mathcal{H}})\]

만약 현재 policy의 엔트로피가 하한선 $ \bar{\mathcal{H}}$ 보다 낮다면 $ \alpha $ 의 계수가 음수이기 때문에 $ \alpha $는 커지는 방향으로 업데이트될 것이고, 결과적으로 Objective에서 엔트로피의 비중을 늘려 policy의 엔트로피가 커지는 방향으로 유도됩니다. 마찬가지로 엔트로피가 너무 큰 상태면 $ \alpha $가 줄어들면서 보상의 비중이 더 커지게 됩니다. 즉 현재 policy의 엔트로피가 하한선과 비슷한 크기로 유지되게 $ \alpha $가 업데이트 되는 것입니다.

Results

실제로 여러 태스크에서 수행한 벤치마크 결과입니다.

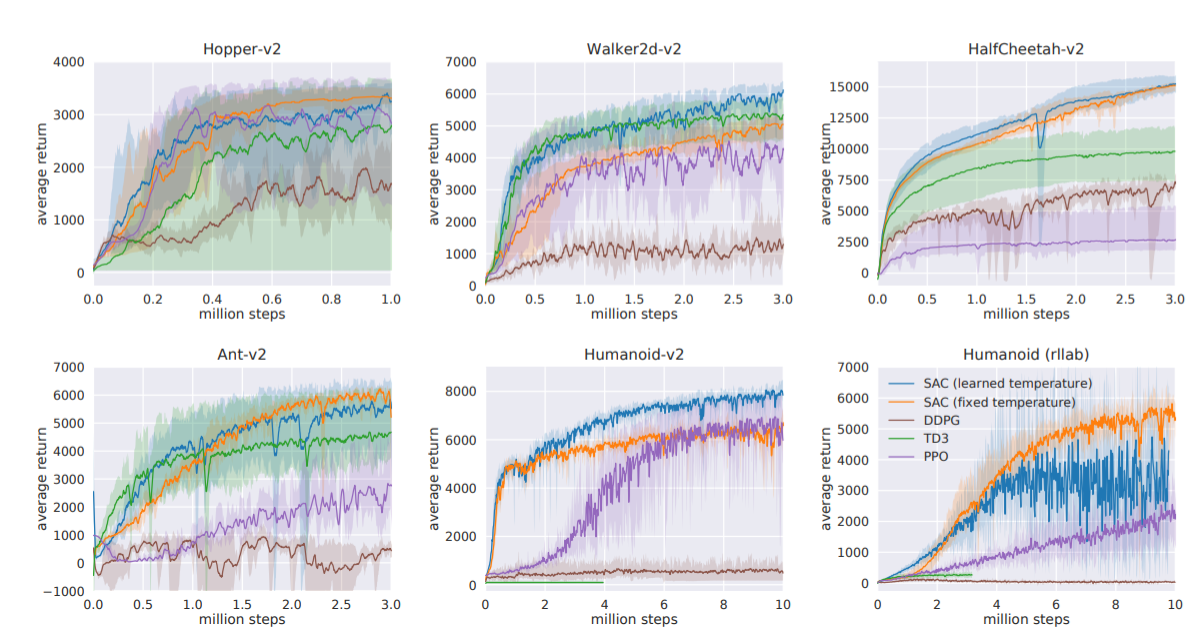
거의 모든 태스크에서 SAC가 최상위권에 위치하고, Entropy Coefficient를 자동으로 학습하게 한 경우가 수동으로 설정한 경우에 비해 나쁘지 않음을 확인할 수 있습니다.

그 외 현실의 사족보행 로봇에 적용했을 때도 본 적이 없는 상황에 대해서 의도한 대로 robust하게 동작하였고, Dexterous Hand를 사용한 태스크에서도 PPO보다 거의 두배 가량 빠른 학습 속도를 보여주었습니다.

Discussion

아쉬운 점 중 하나는 Tabular 세팅에서의 Soft Policy Iteration에서 Soft Actor-Critic으로 넘어갈 때 여러 가정들이 무시되는 부분입니다. Action space의 크기가 finite 하다는 가정도 깨졌고, 현재 policy의 value function으로 완전히 수렴 후 improvement 한다는 가정도 깨졌기 때문입니다. 다만 이는 대부분의 RL 알고리즘이 공통적으로 가지는 문제이기 때문에 크게 아쉬운 점은 아니라고 생각합니다.

엔트로피 계수를 조정하는 부분에선 각 timestep에 대한 라그랑지안 함수의 최적 파라미터를 계산할 때, 초기 $ \alpha_t $ 에 대해 optimal policy를 계산한 뒤, 그 optimal policy에 대한 optimal entropy coefficient를 찾는데 이것이 global하게 optimal한 policy, coefficient 인지에 관한 설명이 없습니다(아마 아닐 것 같습니다).

또한 이론적으로는 각 timestep마다 최적의 policy를 찾고 그에 대응되는 최적의 coefficient를 찾았다 해도 실제 알고리즘에서는 현재 policy에 대해서만 coefficient를 찾는다는 한계가 있습니다. Timestep 별 policy야 이론적으로 하나의 policy를 잘 학습시키면 각 timestep에 대해 최적의 policy와 동일한 결과를 보이게 할 수 있겠지만, $ \alpha $ 를 모든 timestep에 대해 같은 값을 사용하는 것은 수학적으로는 비약이 있어 보입니다. 다만 $ \alpha $ 에 대한 최적화 목표를 직관적으로 해석했을 때는 이해되는 부분이긴 합니다.

=========