소개
안녕하세요. 이번 글에서는 반평면 교집합(Half Plane Intersection)에 대해 소개해드리려고 합니다. 반평면 교집합으로 풀 수 있는 몇 가지 재미있는 문제들이 있는데, 생각보다 관련 자료가 많지 않아서 간단하게나마 정리해 보았습니다.
Half Plane Intersection
반평면(Half Plane)이란, 평면 상에 하나의 직선을 그었을 때 나누어지는 각각의 영역을 말합니다.

반평면들이 여러 개 모이면 그 교집합의 형태는 아래와 같이 볼록 다각형(convex hull)이 됩니다.

그럼 대체 이 교집합을 알면 어디에 써먹을 수 있을까요? 후술하겠지만 대표적으로는 볼록 다각형의 내접원을 구하는 데 활용할 수 있습니다. 우선은 반평면 교집합을 구하는 알고리즘을 먼저 살펴보고, 이후 몇 가지 응용 문제들을 소개하도록 하겠습니다.
알고리즘을 소개하기에 앞서 반평면을 수식으로 정의할 필요가 있습니다. 반평면을 표현하는 방법에는 여러 가지가 있을 수 있는데, 여기에서는 알고리즘 구현을 단순하게 하기 위해 벡터로 표현하는 방법을 사용할 것입니다.
벡터 표현법에도 여러 가지가 있을 수 있지만, 여기에서는 위치 벡터와 탄젠트 벡터를 이용해 반평면을 정의하려고 합니다. 위치 벡터 $\vec{p}$ 와 탄젠트 벡터 $\vec{t}$ 가 주어지면, 그에 해당하는 반평면은 $\vec{p}$에서 $\vec{p}+\vec{t}$ 를 바라보았을 때 나뉘는 두 영역 중 왼쪽 영역으로 정의하겠습니다.
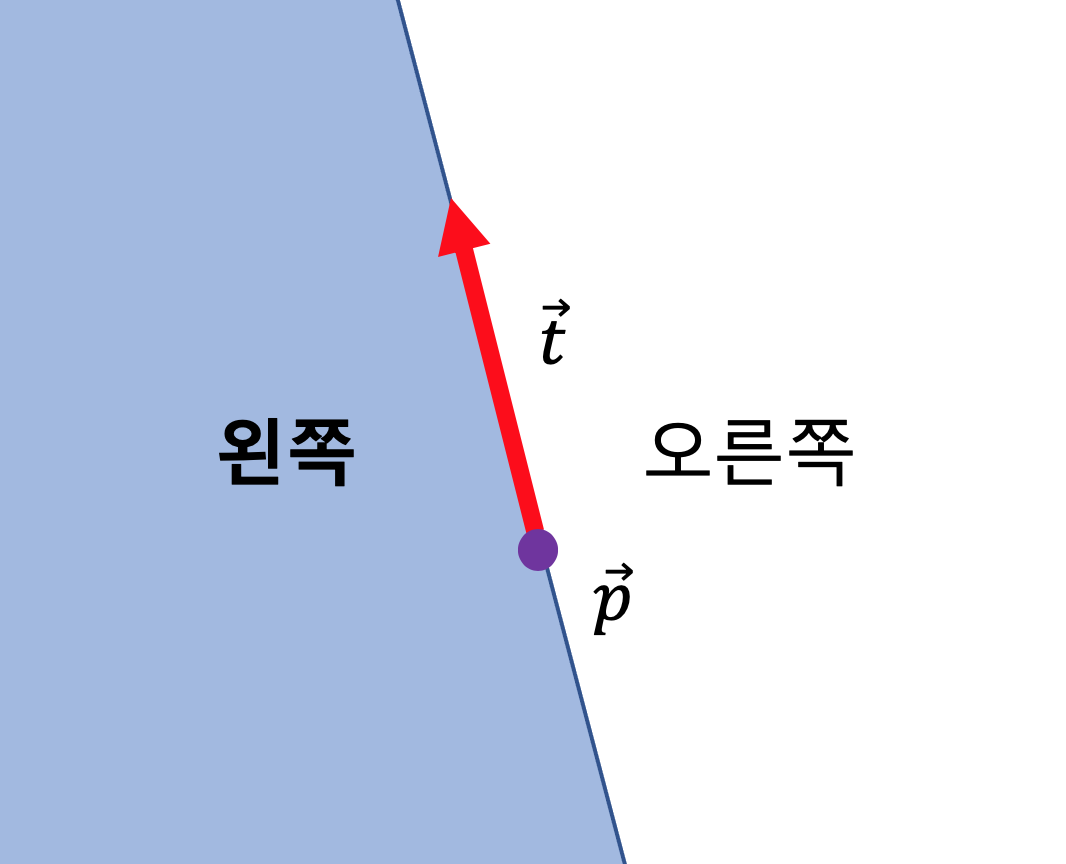
이제 이러한 반평면들의 교집합을 계산하는 방법에 대해 알아볼 것입니다. 즉, 우리가 해야할 일은 교집합에서 볼록다각형을 구성하는 각 꼭짓점들의 위치를 구하는 것입니다. 먼저 단순한 아이디어의 $O(n^3)$ 알고리즘을 소개하고, 좀 더 효율적인 $O(nlogn)$ 알고리즘도 소개하도록 하겠습니다.
(참고로 아래에서 언급할 모든 ‘반평면’이라는 용어는 점들의 집합을 의미하기도 하고, 반평면을 구분하는 경계선을 의미하기도 합니다. 이를테면 ‘두 반평면의 교점’이라고 한다면 ‘두 반평면의 경계선의 교점’으로 이해하시면 되겠습니다.)
$O(n^3)$ 알고리즘
교집합의 형태를 약간 관찰해보면, 볼록 다각형을 이루는 모든 꼭짓점은 임의의 두 반평면 경계의 교점임을 알 수 있습니다. 즉, $n^2$개의 교점 후보들에 대해 볼록 다각형에 포함되는지 여부를 판단하면 됩니다. 볼록 다각형에 포함된다는 것은 모든 반평면 내부에 속하는 것과 같은 의미이므로, 하나의 점을 판단하기 위해 $n$개의 반평면을 확인해야 합니다. 반평면에 속하는지 여부는 ccw 등으로 쉽게 판단할 수 있습니다. 이 과정을 그대로 구현하면 총 시간복잡도는 $O(n^3)$ 이 됩니다. 사실 $O(nlogn)$ 알고리즘에 비해 구현이 딱히 간단한 것만도 아니라(..) 아직 실제로 구현해서 사용해본 적은 없습니다. pseudocode만 남기도록 하겠습니다.
function HPI(h[1..n])
// h[1..n] : h[i] is i-th half plane
// res[] : result list of the points (initially empty)
for i=1 to n
for j=i+1 to n
for k=1 to n
p <- intersection point of h[i] and h[j]
if p is in h[k]
insert p to res
sort res by angle
return res
$O(nlogn)$ 알고리즘
$O(nlogn)$ 알고리즘은 convex hull trick의 알고리즘과 아주 유사합니다. (혹시 convex hull trick을 모르신다면 해당 내용을 먼저 찾아보시는 걸 추천드립니다.) 반평면들을 각도 순으로 정렬하고, 각도가 작은 반평면부터 차례대로 덱(deque)에 삽입합니다. 이때 기존 덱에 존재하던 반평면들 중 일부는 새로 삽입되는 반평면에 의해 제거 대상이 됩니다. 즉, 덱에는 실질적으로 볼록 다각형을 구성하는 반평면들만 유지합니다. 모든 반평면들을 적절히 삽입하고 나면 최종적으로 덱에는 반평면 교집합을 구성하는 원소들이 남게 됩니다.
그럼 삽입하는 과정에서 제거 대상이 되는 반평면들은 어떻게 알 수 있을까요? 우선 아래 그림처럼 덱의 뒤쪽에서 새로운 반평면에 의해 가려지게 되는 반평면들이 존재할 수 있습니다. (좀 알아보기 쉽게 하고자 교집합을 흰 부분으로 나타내었습니다.)
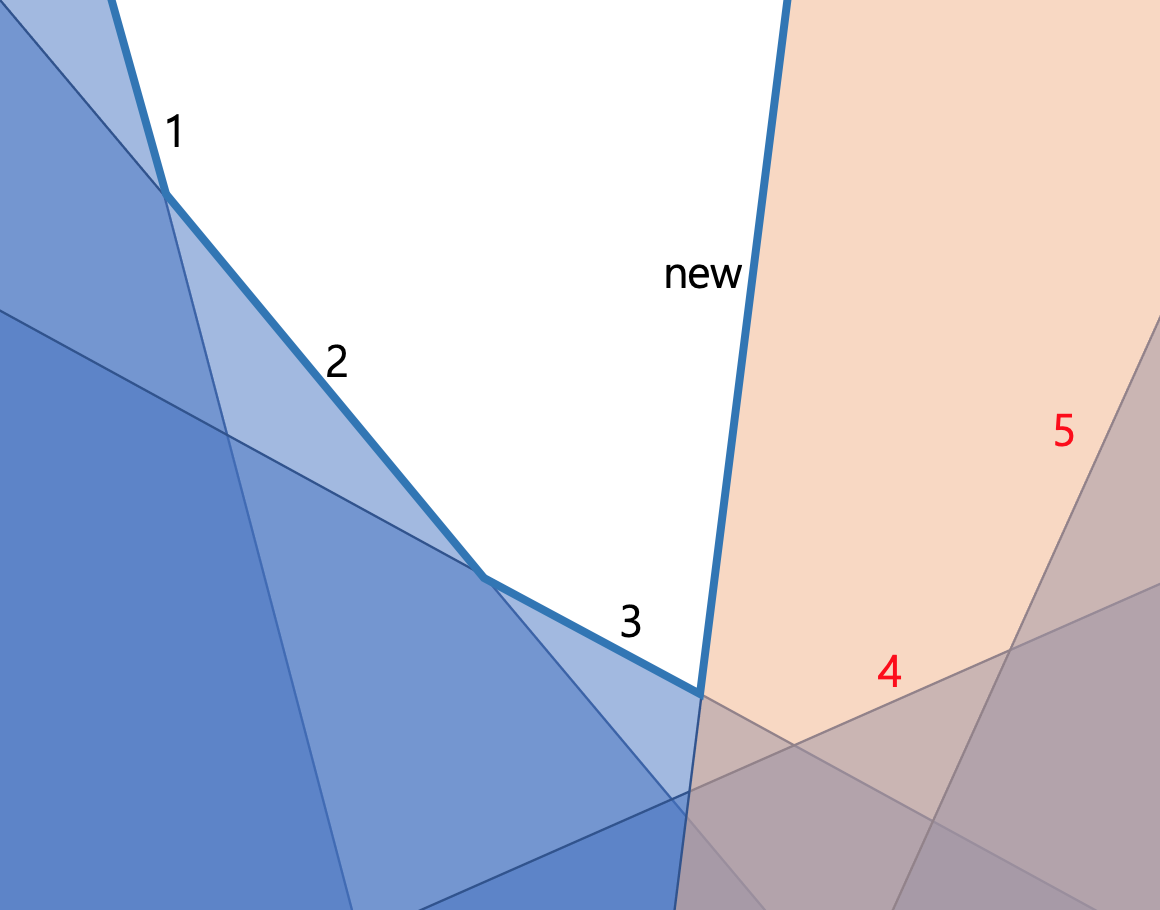
어떤 반평면이 가려진다는 것은, 그 반평면과 인접한 교점들이 새로운 반평면에 포함되지 않음을 의미합니다. 표현이 약간 헷갈릴 수 있는데, 이 부분은 본질적으로 convex hull trick에서 했던 것과 다르지 않습니다. 덱의 마지막 두 반평면의 교점이 새로운 반평면에 포함되지 않는다면 마지막 반평면은 가려지므로 pop back합니다. 마지막 반평면이 가려지지 않을 때까지 이 과정을 반복하면 뒤쪽의 가려지는 반평면들을 모두 제거할 수 있습니다.
다른 경우는 없을까요? 약간 관찰해보면, 다음 그림처럼 덱의 앞쪽에서도 가려지는 반평면들이 존재할 수 있습니다. 뒤쪽에서와 같은 방법으로 앞쪽의 가려지는 반평면들을 모두 제거할 수 있습니다.
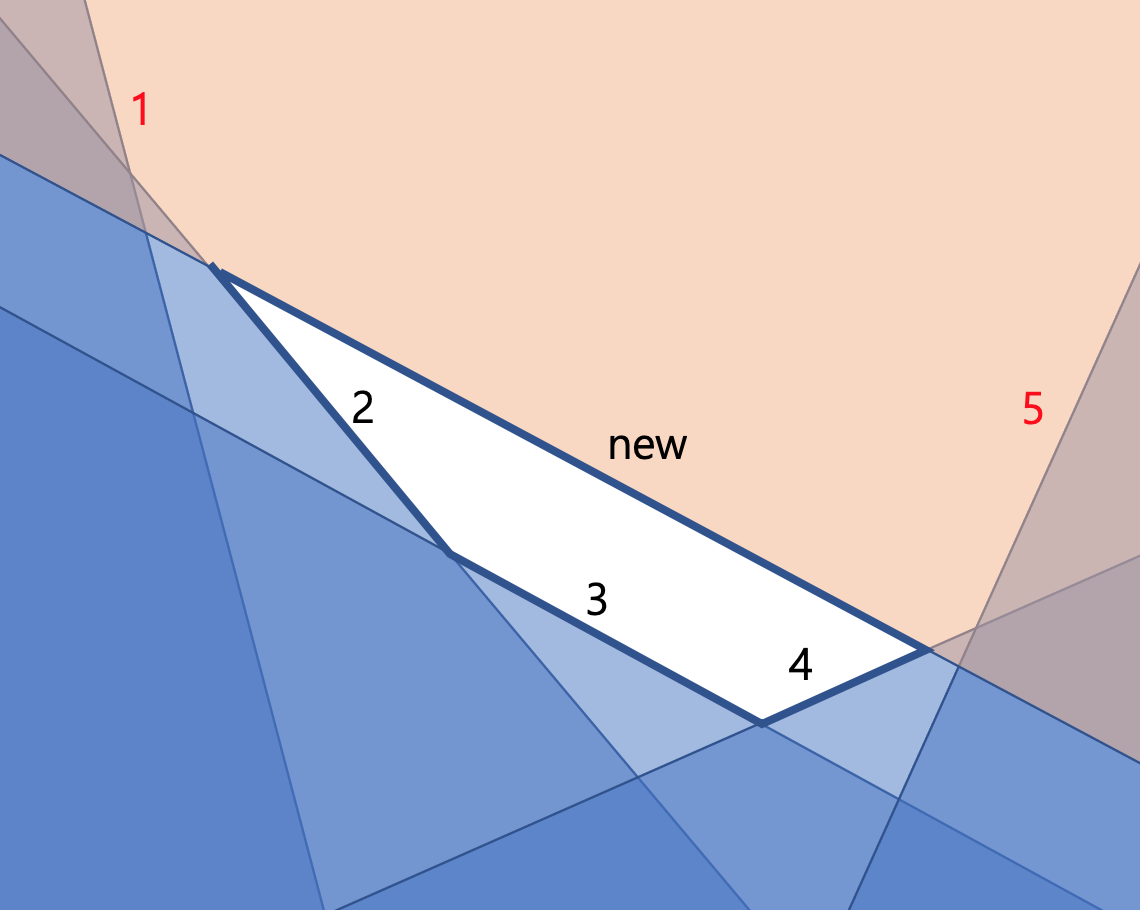
다행히(?) 반평면들이 convex한 모양을 유지하기 때문에 중간에서만 제거되는 경우는 존재하지 않습니다. 따라서 덱의 앞, 뒤쪽에 대해서만 조건들을 확인해주고 새로운 반평면을 삽입하면 됩니다.
다만 한 가지 조건을 더 확인해 주어야 하는데, 바로 새로운 반평면 자체가 아래 그림처럼 기존 반평면들에 의해 가려지는 경우입니다.
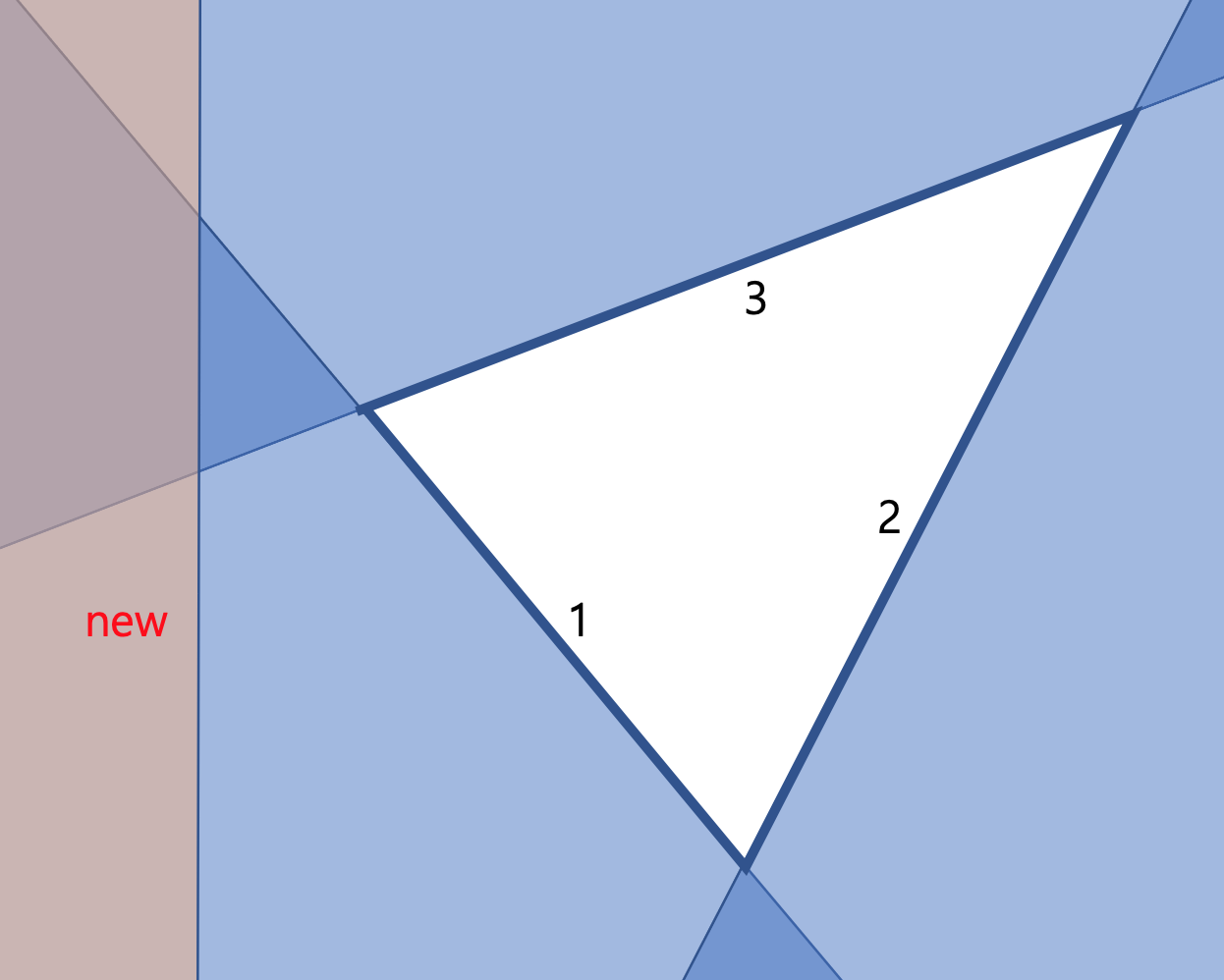
이러한 상황에서는 새로운 반평면을 삽입하면 안 됩니다. convex hull trick에서는 새로 삽입하려는 직선이 기존 직선들에 의해 가려지는 경우가 없지만(위쪽이 뚫려있기 때문에), 반평면 교집합에서는 덱의 앞, 뒤 반평면이 연결되어 닫힌 다각형을 구성하기 때문에 다각형 밖에 반평면이 위치할 경우 가려지게 됩니다. 가려지는지의 여부를 판단하는 방법은 새로운 반평면과 덱의 마지막 반평면의 교점이 덱의 처음 반평면에 속하는지 판단하면 됩니다. (처음과 마지막의 순서는 상관 없습니다.)
여기까지가 알고리즘의 전부입니다. 반평면을 각도 정렬하는 시간은 $O(nlogn)$이고, 모든 반평면은 덱에 최대 한 번 삽입/삭제되므로 덱을 구성하는 시간은 $O(n)$입니다. 따라서 총 시간복잡도는 $O(nlogn)$입니다. 구현 난이도도 $O(n^3)$ 알고리즘에 비해 크게 어렵지 않습니다.
#include <bits/stdc++.h>
#define sz(x) ((int)x.size())
typedef long long ll;
typedef long double ld;
struct point {
ld x,y;
point() {}
point(ld x,ld y):x(x),y(y) {}
};
struct line {
point s, t;
line() {}
line(point s, point t) : s(s), t(t) {}
};
inline bool equals(ld a, ld b) { return abs(a - b) < 1e-9; }
bool line_intersect(point& s1, point& e1, point& s2, point& e2, point& v) {
ld vx1 = e1.x - s1.x, vy1 = e1.y - s1.y;
ld vx2 = e2.x - s2.x, vy2 = e2.y - s2.y;
ld det = vx1 * (-vy2) - (-vx2) * vy1;
if(equals(det, 0)) return 0;
ld s = (ld)((s2.x - s1.x) * (-vy2) + (s2.y - s1.y) * vx2) / det;
v.x = s1.x + vx1 * s;
v.y = s1.y + vy1 * s;
return 1;
}
bool bad(line& a, line& b, line& c) {
point v;
if(!line_intersect(a.s,a.t,b.s,b.t,v)) return 0;
ld crs = (c.t.x-c.s.x)*(v.y-c.s.y)-(c.t.y-c.s.y)*(v.x-c.s.x);
return crs < 0 || equals(crs, 0);
}
vector<point> HPI(vector<line>& ln) {
auto lsgn = [&](const line& a) {
if(a.s.y == a.t.y) return a.s.x > a.t.x;
return a.s.y > a.t.y;
};
sort(ln.begin(), ln.end(), [&](const line& a, const line& b) {
if(lsgn(a) != lsgn(b)) return lsgn(a) < lsgn(b);
return (a.t.x-a.s.x)*(b.t.y-b.s.y)-(a.t.y-a.s.y)*(b.t.x-b.s.x)>0;
});
deque<line> dq;
for(int i=0; i<sz(ln); i++) {
while(dq.size() >= 2 && bad(dq[dq.size()-2], dq.back(), ln[i]))
dq.pop_back();
while(dq.size() >= 2 && bad(dq[0], dq[1], ln[i]))
dq.pop_front();
if(dq.size() < 2 || !bad(dq.back(), ln[i], dq[0]))
dq.push_back(ln[i]);
}
vector<point> res;
if(dq.size() >= 3) for(int i=0; i<sz(dq); i++) {
int j=(i+1)%sz(dq);
point v;
if(!line_intersect(dq[i].s, dq[i].t, dq[j].s, dq[j].t, v)) continue;
res.push_back(v);
}
return res;
}
문제 1 - Most Distant Point from the Sea (boj.kr/3903)
먼저 소개해드릴 문제는 ICPC Tokyo Regional 2007 기출문제인 “Most Distant Point from the Sea”입니다. 말 그대로 볼록 다각형 모양의 섬에서 바다와 가장 멀리 떨어진 지점이 어디인지 찾는 문제입니다. (정확히는 그 거리를 구하면 됩니다.)
이 문제를 “바다로부터의 거리가 $r$ 이상인 점이 존재하는가”로 바꿔 풀어봅시다. 이 물음에 답할 수 있다면 이분 탐색을 통해 답을 구할 수 있을 것입니다.
바다로부터의 거리가 $r$ 이상이라는 것은, 볼록 다각형 외부의 모든 점에서 반지름 $r$인 원을 그렸을 때 그 안에 포함되지 않는다는 것입니다. 그리고 이러한 원들의 합집합의 형태를 생각해보면, 아래 그림처럼 볼록 다각형의 각 변을 안쪽으로 $r$ 만큼 이동시킨 곳에 경계가 생기게 됩니다.
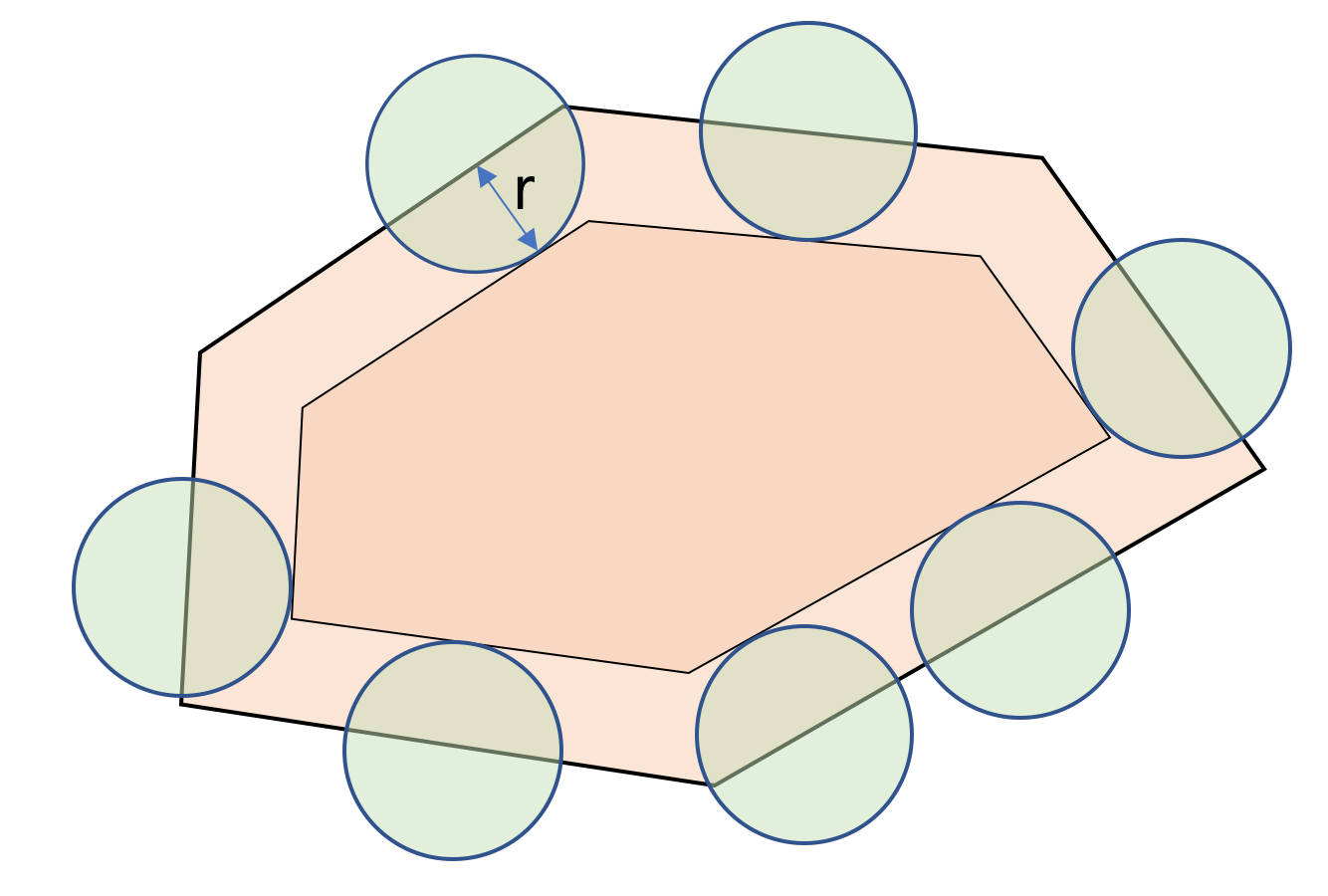
여기서 각 변은 반평면 경계라고 생각할 수 있습니다. 즉, 경계를 기준으로 볼록 다각형의 안쪽을 향하는 곳에 점이 위치해야 한다는 일종의 조건인 것입니다. 이러한 조건들을 모두 만족하는 점이 하나라도 존재한다면, 즉 반평면 교집합이 공집합이 아니라면 거리가 $r$ 이상인 점이 존재하게 됩니다. 요약하자면 볼록 다각형을 구성하는 $n$개의 변에 대해 안쪽으로 $r$만큼 이동시킨 반평면을 구하고, 이들의 교집합을 상술한 $O(nlogn)$ 알고리즘으로 계산하여 공집합 여부를 판단하면 됩니다. 여기에 이분탐색을 더해 총 시간복잡도는 $O(nlognlog(좌표범위))$ 가 됩니다. 눈치채셨을 수 있지만, 이 문제에서 구하고자 하는 것은 결국 볼록 다각형의 최대 내접원의 반지름입니다.
문제 2 - 2 circles (boj.kr/5255)
다음 소개드릴 문제는 BOI(Balkan) 2011 기출문제인 “2 circles”입니다. 앞서 소개한 문제가 볼록 다각형의 최대 내접원을 구하는 것이었다면, 이 문제는 볼록 다각형 내에 겹치지 않게 넣을 수 있는 동일한 크기의 두 원의 최대 반지름을 구하는 것입니다.
마찬가지로 “반지름이 $r$인 두 원을 겹치지 않게 넣을 수 있는가”를 판단하여 이분 탐색으로 접근해봅시다. 사실 앞의 문제를 해결했다면 이 문제 역시 쉽게 해결할 수 있습니다. 앞에서 한 것처럼 볼록 다각형의 각 변을 안쪽으로 $r$만큼 이동시킨 반평면을 계산하고 이들의 교집합을 구합니다. 그러면 이 교집합은 곧 반지름 $r$인 원이 볼록 다각형을 벗어나지 않게 놓을 수 있는 중심 좌표의 범위에 해당합니다. 따라서 우리가 고려해야 할 것은 두 원이 겹치지 않게, 즉 중심 사이의 거리가 $2r$ 이상이 되도록 교집합에서 두 원의 중심점을 선택할 수 있는지 판단하는 것입니다.
쉽게 알 수 있는 것은, 교집합에서 가장 먼 두 점의 거리가 $2r$ 이상이라면 그러한 조건을 만족하는 두 점이 존재하고(가장 먼 두 점), $2r$보 작으면 존재하지 않습니다. 그런데 교집합의 형태가 볼록 다각형이기 때문에, 가장 먼 두 점의 거리는 잘 알려진 rotating calipus 알고리즘으로 $O(n)$ 에 구할 수 있습니다. 따라서 시간복잡도는 반평면 교집합이 좌우하여 $O(nlogn)$이고, 이분탐색까지 고려한 총 시간복잡도는 $O(nlognlog좌표범위)$ 입니다.
문제 3 - Jungle Outpost (boj.kr/3527)
마지막 문제는 NEERC 2010 기출문제인 “Jungle Outpost”입니다. 이 문제에서는 볼록 다각형이 하나 주어집니다. 이때 볼록 다각형에서 어떤 $k$개의 정점을 제거하더라도 남은 $n-k$개 정점들의 convex hull 안에 반드시 포함되는 점이 존재한다면 그 $k$는 good이라고 합시다. 문제는 good인 최대의 $k$를 찾는 것입니다. (설명이 미흡하여 원문을 읽는 것을 추천드립니다.)
이 문제도 이분탐색으로 접근할 수 있습니다. 그리고 약간 생각해보면, 모든 $a_i$와 $a_{i+k+1}$를 연결한 반평면들의 교집합을 구했을 때 공집합이 아니면 good임을 알 수 있습니다. 다시 말해 어떤 연속한 $k$개의 정점들을 제거해도 살아있는 정점이 존재한다면 good, 그렇지 않다면 bad입니다. (문제에서는 반드시 연속한 정점들을 제거해야 한다는 조건은 없지만, 연속하게 제거하는 것이 볼록 다각형을 커버하는 데에 더 이득이라는 것을 알 수 있습니다.) 나머지는 반평면 교집합과 이분탐색을 적용하면 되므로 더 자세한 설명은 생략하겠습니다.