September 18, 2019 02:00

안녕하세요, 이번 글에서는 Persistent Segment Tree 에 대해 알아보도록 하겠습니다.

Segment Tree

Persistent Segment Tree를 이해하기 위해서는 Segment Tree에 대한 이해가 선행되어야 합니다. 이미 대다수의 독자분들이 Segment Tree에 대해 알고 있겠지만 다시 한 번 짚고 넘어가겠습니다.

Segment Tree는 배열을 여러 구간으로 나누어 관리하는 구조로, $N$개의 원소가 있을 때 구현에 따라 2배에서 4배 정도의 추가 공간이 필요하지만 원소의 변경, 특정 범위 내의 원소의 연산을 $lgN$에 수행할 수 있습니다.

구체적으로 배열 1 2 3 4 3 2 1 6을 가지고 합을 관리하는 Segment Tree를 만들면 아래와 같이 만들어집니다.

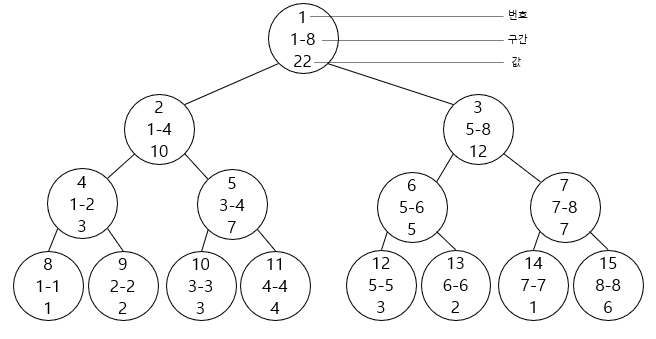
각 노드는 자신이 대표하는 구간의 원소의 합을 저장하고 있습니다. 예를 들어 만약 2부터 7까지의 합을 구하고 싶으면 9번, 5번, 6번, 7번 노드의 값을 합하면 됩니다. 이와 같이 최대 길이가 $N$인 구간의 합을 $lg N$개의 노드를 이용해 알 수 있습니다. 누적 합(Prefix Sum)을 이용하면 $O(N)$에 Segment Tree를 만들 수 있으나 아래에서 설명할 값의 변경을 $N$번 수행하는 방식으로 $O(NlgN)$에 Segment Tree를 만들어도 크게 문제가 없습니다.

Segment Tree에서 특정 원소의 값을 바꿀 경우, 노드에서 값을 바꿔야 하는 원소의 갯수는 $lg N$에 비례합니다. 예를 들어 3번 원소의 값을 바꾸게 될 경우 1번, 2번, 5번, 10번 노드의 값을 바꾸면 됩니다.

즉 Segment Tree에서는 구간의 합과 특정 원소의 변경을 모두 $lg N$에 구할 수 있습니다. 구현은 아래와 같이 이루어집니다.

int seg[32];

void upd(int i, int x, int nidx, int node_st, int node_en){
  if(i < node_st or i > node_en) return;
  seg[nidx] += x;
  if(node_st != node_en){
    int mid = (node_st + node_en) / 2;
    upd(i, x, 2*nidx, node_st, mid);
    upd(i, x, 2*nidx+1, mid+1, node_en);
  }
}

// arr[i]를 x만큼 증가시킨다.
void upd(int i, int x){
  upd(i, x, 1, 1, 8);
}

// nidx번째 노드에서 (i, j) 구간과 겹치는 부분의 합을 반환하는 함수
int query(int i, int j, int nidx, int node_st, int node_en){
  if(j < node_st or i > node_en) return 0;
  else if(i <= node_st and node_en <= j) return seg[nidx];
  int mid = (node_st + node_en) / 2;
  return query(i, j, 2*nidx, node_st, mid) + query(i, j, 2*nidx+1, mid+1, node_en);  
}

// i부터 j까지의 합을 구한다.
int query(int i, int j){
  return query(i, j, 1, 1, 8);
}

Dynamic Segment Tree

이번에는 Sparse한 배열에서 Segment Tree를 만들고 싶다고 해봅시다. 인덱스는 최대 10억까지이지만 실제로 값이 바꾸어지거나 합을 구하도록 요청이 들어오는 횟수는 100만번 이내입니다. 만약 모든 요청을 다 받고난 후에 처리가 가능하다면(=오프라인 쿼리라면) 좌표압축을 통해 해결이 가능합니다. 그러나 요청을 실시간으로 처리해야하는 문제라면(=온라인 쿼리라면) 좌표압축을 할 수가 없고, 그렇다고 10억까지의 범위에 대해 Segment Tree를 미리 구축할 수도 없습니다. 이런 상황에서는 Segment Tree에서 모든 노드를 만들어두는 대신, 필요한 만큼만 노드를 생성하는 기법이 필요합니다. 아래의 예시를 참고해보세요(엄밀히 말해 합을 구하는 쿼리에 대해서는 굳이 노드를 새로 만들 필요가 없이 빈 노드를 참조해야 하면 0을 반환하게끔 하는 방식으로 더 최적화를 시킬 수는 있지만 생략했습니다).

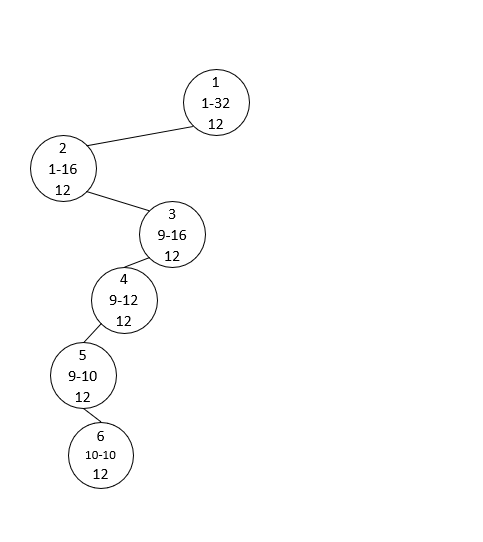
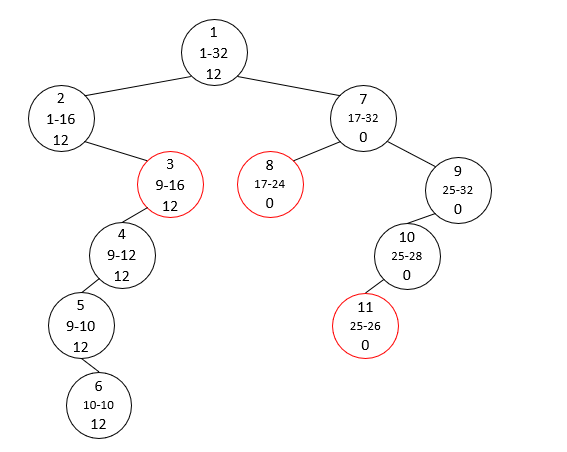
이전의 Segment Tree에서는 왼쪽 자식과 오른쪽 자식의 인덱스를 각각 $2k$, $2k+1$로 쉽게 계산할 수 있었지만 Dyanmic Segment Tree에서는 각 노드가 왼쪽 자식과 오른쪽 자식의 인덱스를 저장하고 있어야 합니다.

Linked List에서 구현하는 방식과 같이 자식들의 포인터를 가지고 있어도 상관이 없지만 인덱스는 일반적으로 4바이트를 차지하는 반면 포인터는 64비트 환경에서 8바이트를 차지하므로 메모리 절약을 위해 인덱스를 저장하는 것이 더 효율적입니다. 아래와 같이 구현할 수 있습니다.

class Node{
public:
  int l, r, val;
};

vector<Node> node(2); // 0번째 : dummy node, 1번째 : root

void upd(int i, int x, int nidx, int node_st, int node_en){
  if(i < node_st or i > node_en) return;
  node[nidx].val += x;
  if(node_st != node_en){
    int mid = (node_st + node_en) / 2;
    if(i <= mid){
      if(node[nidx].l == 0){
        node.push_back({0, 0, 0});
        node[nidx].l = node.size() - 1;
      }
      upd(i, x, node[nidx].l, node_st, mid);
    }
    else{
      if(node[nidx].r == 0){
        node.push_back({0, 0, 0});
        node[nidx].r = node.size() - 1;
      }
      upd(i, x, node[nidx].r, mid+1, node_en);
    }
  }
}

// arr[i]를 x만큼 증가시킨다.
void upd(int i, int x){
  upd(i, x, 1, 1, 1000000000);
}

// nidx번째 노드에서 (i, j) 구간과 겹치는 부분의 합을 반환하는 함수
int query(int i, int j, int nidx, int node_st, int node_en){
  if(j < node_st or i > node_en) return 0;
  else if(i <= node_st and j >= node_en) return node[nidx].val;
  int mid = (node_st + node_en) / 2;
  int ret = 0;
  if(i <= mid){
    if(node[nidx].l == 0){
      node.push_back({0, 0, 0});
      node[nidx].l = node.size() - 1;
    }
    ret += query(i, j, node[nidx].l, node_st, mid);
  }
  if(j >= mid+1){
    if(node[nidx].r == 0){
      node.push_back({0, 0, 0});
      node[nidx].r = node.size() - 1;
    }
    ret += query(i, j, node[nidx].r, mid+1, node_en);    
  }
  return ret;
}

// i부터 j까지의 합을 구한다.
int query(int i, int j){
  return query(i, j, 1, 1, 1000000000);
}

Persistent Segment Tree

이제 Persistent Segment Tree를 다뤄봅시다. Persistent Segment Tree는 여러 개의 Segment Tree를 효율적으로 관리하는 자료구조입니다. 구조에 대해 설명하기에 앞서 Persistent Segment Tree를 이용해 해결할 수 있는 문제를 설명드리겠습니다.

N*N 2차원 공간에 M개의 점이 있다. 특정 영역에 포함되어 있는 점의 갯수를 반환하는 쿼리를 Q개 처리해야 한다.

이 문제에서 N이 5000 이하로 그다지 크지 않다면 이 문제는 아주 그럭저럭 간단한 Dynamic Programming 문제입니다. 그런데 N이 10만이라면 DP로 해결이 불가능합니다. 어떻게 해결할 수 있을까요?

문제의 관점을 바꾸어 일차원에서 M개의 점이 있고 특정 영역에 포함되어 있는 점의 갯수를 반환하는 문제였다고 해봅시다. 그렇다면 이 문제는 특정 원소의 값을 1로 두고 구간의 합을 처리해야하는 문제이니 Segment Tree로 쉽게 해결이 가능합니다.

2차원이라고 해도 아래와 같이 Segment Tree를 N개 둘 수만 있다면 문제를 그다지 어렵지 않게 해결할 수 있습니다. 우선 아래의 그림과 같이 각 칸에 대해, 같은 열에서 자신을 포함한 아래 영역에서의 점의 갯수를 저장해두었다고 해봅시다. 그리고 각 행에 대해 Segment Tree를 만들어두었으면 그러면 내가 원하는 영역에서 점의 갯수는 곧 두 개의 Segment Tree에서 구간의 합을 계산하는 문제와 동일합니다. 주어진 그림에서 황금색 영역의 점의 갯수는 파란색 구간의 합에서 빨간색 구간의 합을 뺀 값입니다.

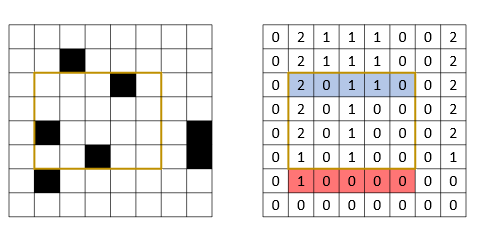
여기서 문제는 N개의 원소를 담은 N개의 Segment Tree를 만드는 것은 $N^2$의 공간이 필요하기 때문에 불가능하다는 점입니다. 이 점을 영리하게 해결하기 위해서는 각 N개의 Segment Tree에서 중복된 노드가 굉장히 많다는 점입니다.

새로운 점이 추가될 때 마다 최대 $lg N$개의 노드의 값만 변경되기 때문에 점이 $M$개일 경우 굳이 노드를 $N^2$개를 만들 필요가 없고 $N + MlgN$개만 만들면 됨을 알 수 있고 이와 같이 중복되는 노드를 활용해 N개의 Segment Tree를 효과적으로 두는 것이 Persistent Segment Tree의 핵심입니다.

첫 번째 Segment Tree는 원소 1 2 3 4 3 2 1 6으로 이루어져있고 두 번째는 원소 1 2 3 7 3 2 1 6으로 이루어진 상황을 그림으로 표현하면 아래와 같습니다. 노드 번호를 주의깊게 확인해주세요.

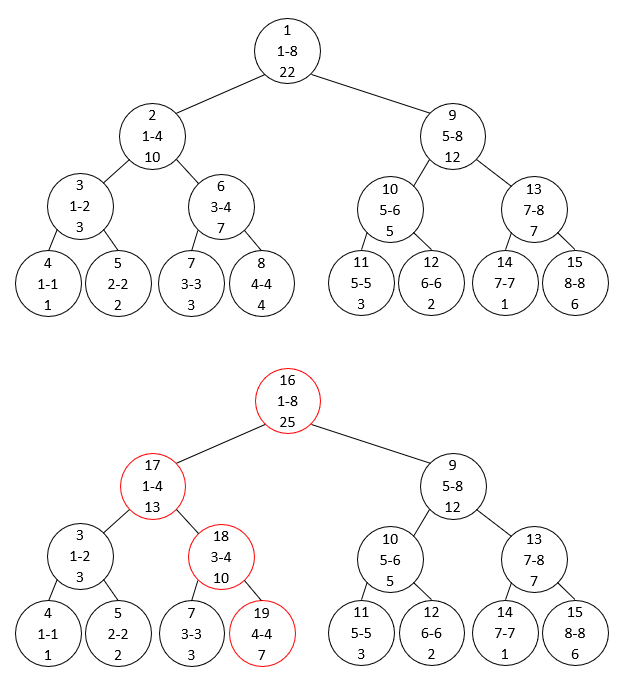
4번째 원소가 바뀜에 따라 4개의 노드는 변경이 필요하지만 나머지 노드는 그냥 그대로 가져오면 됩니다.

어느 정도 개념을 잡았더라도 구현에서 다소 애를 먹을 수 있습니다. Persistent Segment Tree의 개념을 잡기 위해 예로 든 이차원 상의 점 갯수를 세는 문제는 BOJ 11012번 - Egg(링크)에서 확인할 수 있습니다. 정답 코드를 확인해보세요.

이외에도 BOJ 13538번 - XOR 쿼리(링크), BOJ 11932번 - 트리와 K번째 수(링크) 등의 문제가 Persistent Segment Tree로 해결할 수 있는 문제입니다.

결론 및 제언

Persistent Segment Tree는 다소 난이도가 있는 쿼리 문제를 해결하기 위해 반드시 알아야하는 자료구조입니다. Segment Tree에 충분히 익숙하지 않다면 구현에 어려움을 겪기 쉬우나, Dynamic Segment Tree와 비슷한 느낌의 구조에 익숙해진다면 팀노트의 도움 없이도 구현을 그다지 어렵지 않게 해낼 수 있습니다.

저는 작년 8월쯤에 처음으로 Persistent Segment Tree에 대해 공부했는데 당시 제가 다른 분들의 글로부터 도움을 받은 것과 같이 이 글이 고급 알고리즘을 하나씩 정복하고자 하는 독자분들에게 도움이 되면 좋겠습니다.